捣固与打磨复合作业下有砟轨道几何不平顺预测模型

许玉德， 吴宣庆， 刘思磊， 薛志强， 李少铮， 李长生

（1.同济大学 道路与交通工程教育部重点实验室，上海 201804；2.同济大学 上海市轨道交通结构耐久与系统安全重点实验室，上海 201804；3.上海地铁维护保障有限公司， 上海 200070；4.朔黄铁路发展有限责任公司， 河北 肃宁 062350）

近年来我国铁路不断提速，运输需求不断增加，轨道几何不平顺也因此日益恶化，传统的周期修方式也逐渐向状态修转变。在此背景下，有砟轨道的几何不平顺预测则成为关注的重点。除了列车荷载对有砟轨道不平顺的恶化影响外，捣固与打磨作业作为常见的铁路养护维修方式，可以有效地改善有砟轨道不平顺状态，因此在进行轨道几何不平顺预测时必须考虑二者对轨道不平顺的影响。有砟轨道作为离散、易变形的结构，不同区段会有较大的差异性，为了及时掌握各区段的轨道状态指标，合理地安排捣固、打磨等大机养护维修作业的时机，需要针对不同区段下的有砟轨道几何不平顺值进行准确的预测。

国内外学者多以TQI（即轨道质量指数）为研究对象，建立轨道几何不平顺的预测模型。周宇等［1］以广深线为例，将高低不平顺作为研究对象，综合考虑运量、速度、轨道结构形式、路基状态对轨道恶化的影响，建立了高低不平顺预测模型，但该模型仅仅考虑了高低不平顺值的变化，无法直观预测TQI变化趋势。曲建军等［2-3］利用灰色预测理论，改进了马尔科夫链的随机预测模型，建立了TQI非等时距灰色时变参数模型，成功模拟了TQI 的随机波动特性。赵玉林等［4］提出改进非等时距灰色组合（IGMPSO-Elman）预测模型，对传统灰色模型进行了改进，并利用实测TQI数据进行了可靠性验证。但上述两个模型运算较为复杂，计算不同作业区段时会出现计算量大、现场预测的适用性一般等情况。彭丽宇等［5］利用历年轨检车资料，考虑轨道不平顺变化特点，采用BP神经网络对TQI及各单项的标准差进行预测。贾朝龙等［6-7］利用数据挖掘技术，分析轨道不平顺值的变化趋势，并结合神经网络等前沿数据处理方法，建立了递推预测模型。以上两个模型虽方便计算，但没有考虑捣固与打磨作业的恢复作用，仅仅能够实现恶化规律的预测，无法预测作业后的改善效果。许玉德等［8-10］依据相关理论，采用数值模拟方法，建立了轨道几何不平顺指数型恶化函数以及捣固后恢复函数，实现了捣固作业后轨道不平顺的预测，但上述模型并没有针对打磨作业提出恢复函数。综上所述，建立一个充分考虑不同区段的差异性、便于现场计算且能够考虑捣固与打磨作业对轨道不平顺影响的新型几何不平顺预测模型具有重要意义。

本文在上述研究基础上，建立了捣固与打磨复合作业下的有砟轨道几何不平顺预测模型。根据轨道线路的恶化特点推导了恶化函数类型，进而为方便计算天窗间隔的恶化量定义求解了恶化率函数；之后分别针对捣固与打磨作业对轨道几何状态的影响建立了各自的恢复函数；为方便现场运算，同时考虑不同作业区段的差异性，结合恶化与恢复函数形成了不同区段独特的恶化矩阵，将连续函数离散化，并通过恶化矩阵进行轨道不平顺值的预测。利用京沪线现场实测数据进行模型的可靠性验证，相关数据及图像表明，建立的恶化函数与恢复函数符合现场趋势；通过恶化矩阵进行轨道不平顺的预测可以满足现场需求。

1 轨道不平顺恶化模型的建立

在列车荷载的反复作用下，轨道变形会不断累积，轨道几何不平顺也会不断恶化。本节通过分析有砟轨道几何不平顺值的恶化规律，结合轨道TQI的恶化特点，选定合理的恶化函数类型，建立有砟轨道几何不平顺恶化模型。

1.1 模型基本假设

为使轨道几何不平顺恶化模型便于运算，在保证真实性的前提下对模型作出如下假设：

（1）模型计算步长为1 d。

（2）恶化模型的相关参数由历年轨检车数据决定，不考虑其他因素。

（3）模型中每个作业区段均采用不同恶化函数，即不同作业区段的恶化率不同，以充分考虑不同区段的差异性。

（4）不考虑轨道检测、诊断的时间影响。

1.2 模型基本参数定义

由于不同里程线路的恶化特点不同，在恶化模型中应针对不同的里程设置不同的恶化函数。对模型的基本参数定义如下：

（1）作业区段编号为m，天窗时间编号为l。

（2）恶化率为k，用来描述线路几何不平顺的恶化情况，取值范围为[0，+∞]，与时间、线路、作业情况有关。

（3）时间区段函数为T(l)，是模型中描述线路天窗分布情况的函数。例如T(5)=4表示第5个天窗与第6个天窗间隔为4 d。

1.3 恶化函数类型推导

轨道几何不平顺的恶化速率一般来说不固定，是与不平顺值大小高度相关的一个变量。轨道几何状态越差，列车对道床的动荷载就越大，进而导致线路的几何不平顺恶化速率变大，说明轨道几何状态与恶化速率应存在正相关关系，为方便计算求解，此处假设二者具有线形正相关关系，可以得到关于TQI恶化速率与不平顺值的微分方程

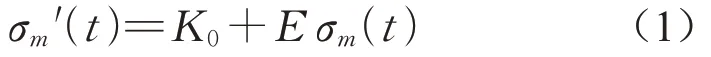
式中：K0、E为任意常数；σm为作业区段m的TQI，mm，是时间t的函数。

计算可得σm随时间变化的通解如下：

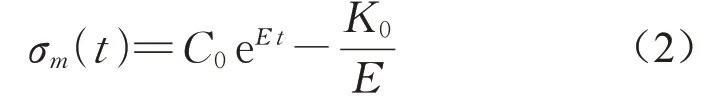
式中：C0为任意常数。

可以发现σm随时间变化的函数类型为指数函数，这与Quiroga等［11］建立的几何不平顺预测函数类型一致，验证了轨道几何状态与恶化速率线形正相关假设的合理性。其中各项参数由初始值和作业区段的恶化速率决定。为方便表述，令恶化函数的最终解析式F(t)如下：

式中：G(σ)=F-1(σ)，二者互为反函数；值域上限10为有砟轨道列车时速大于160 km·h-1时TQI管理值。

1.4 恶化率函数表达式推导

利用式（3）进行TQI预测时，必须确定时间t，然而对于现场来说并不方便。同时在实际应用时，往往希望得到某区段轨道几何不平顺值后，就可以确定该区段在经历一个天窗间隔后轨道不平顺的变化。为了使模型更加适用于现场，需重新定义一个以几何不平顺值为自变量的新函数即恶化率函数，以方便计算天窗间隔恶化量，最终定义恶化率函数为

式（4）中分子为一个天窗间隔的恶化量，将其定义为K(σm，Δt)，即

假设天窗编号为l时时间为t，此时该区段的轨道几何不平顺值为σm，其与天窗编号l+1相隔时间为Δt，依据式（3）与式（5）可得

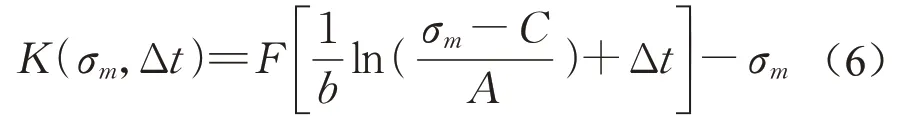
经过化简后可得恶化率函数k为

式中：Δt与天窗编号l为一一映射关系，具体对应关系与线路全年天窗时间安排有关，具体取值方式可根据天窗安排进行查表。拟合参数b、C由作业区段历年来轨检车数据来确定，也可以认为由天窗编号l和作业区段编号m来确定，故恶化率k完全由不平顺值σ、天窗编号l、作业区段编号m这3个值确定。确定恶化率后，可以进行长期的保存与调用，在确定某次天窗的轨道不平顺值以及天窗间隔后可以直接计算得到下一天窗的轨道不平顺值。

2 捣固与打磨作业恢复模型的建立

捣固作业和打磨作业是线路养护维修的主要方式，在进行轨道不平顺预测时，不仅需要确定恶化函数，还要根据作业区段的养修方式确定恢复函数。本节将针对捣固与打磨两种作业方式的特点进行分析，以确定恢复函数模型。

2.1 几何不平顺恢复原理

当轨道几何不平顺值超过管理目标值时，就必须进行养护维修作业。根据沈坚峰［12］阐述的相关理论，捣固作业是降低几何不平顺值的有效方法，打磨作业也可以降低线路的恶化速率，从而间接改善轨道几何不平顺。同时在实际养修作业中，线路捣固作业对TQI各个单项的影响不同，因此将TQI作为模型的研究对象并不合理。邱俊兴等［13］分析了捣固与打磨作业前后各单项不平顺标准差的残留率，认为捣固与打磨作业对轨距单项基本没有改善效果，所以在恢复模型中，TQI也将去掉轨距单项，下文用σN或无轨距的TQI来指代。

2.2 模型基本假设

（1）模型计算步长为1 d。

（2）在同一作业区段内，恢复函数的相关参数由历年轨检车数据决定，不考虑其他因素。

（3）模型中捣固和打磨作业仅考虑线路捣固和线路打磨，不考虑道岔捣固和道岔打磨。

（4）线路捣固作业仅改变无轨距的TQI大小，而线路打磨作业仅改变无轨距的TQI恶化速率。

（5）模型针对每个作业区段有不同的恢复函数。

（6）不考虑轨道检测、诊断的时间影响。

2.3 模型基本参数定义

根据以上模型假设，参数定义如下：

（1）作业区段编号为m，天窗时间编号为l。

（2）无轨距几何不平顺标准差为σNi，j（mm），未包含轨距一项的几何不平顺值，包含左高低、右高低、左轨向、右轨向、水平、三角坑6个单项之和。下标i和j分别表示地点和时间。例如σN6，72表示第6个作业区段在第72个天窗时的无轨距不平顺值。

（3）恢复率为g(σ，m)，用来描述大型养路机械线路捣固作业后线路的恢复情况，取值范围为[0，1)。

2.4 恢复函数推导

2.4.1 捣固作业

沈坚锋［12］从现场线路维修过的区段中发现，捣固作业后的残留率随高低不平顺变化情况如图1所示。由图1可以发现，随着捣固作业前高低不平顺标准差的增大，残留率呈下降趋势，说明恢复率函数应随无轨距TQI的增大而增大；且根据定义，恢复率函数应小于1。

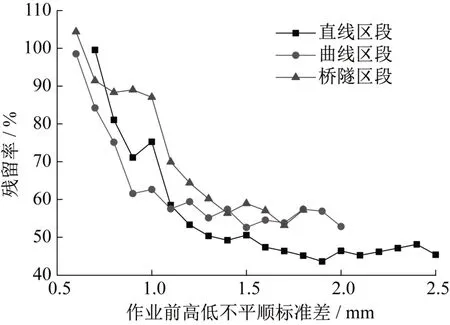
图1 残留率随高低不平顺的变化Fig.1 Residual rate versus height irregularity

故根据上述捣固作业恢复率函数的特点，则对于∀σN∈[0.7，10]（选取无轨距TQI下限为0.7是因为当其小于0.7时，残留率大于100%，此时捣固作业无意义），应有

同时对于同一个作业区段来说，当作业前σN不断增大时，作业后的σN也应不断增大，这才符合现场情况。例如，无轨距的TQI为5 mm的基本作业区域进行捣固作业后的σN值，应该比无轨距的TQI为6 mm的基本作业区域进行捣固作业后的σN值小，线路状态更好。于是，设h(σN，m)为维护后的不平顺值，则有

将式（9）化简后如下：

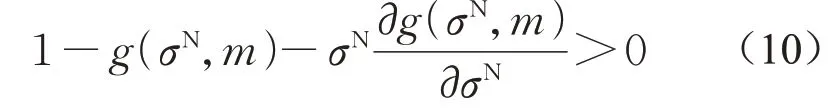
故最终的捣固作业后恢复率函数应满足式（8）与式（10），为方便编程计算，这里采用对数函数进行拟合。即设恢复率函数如下：

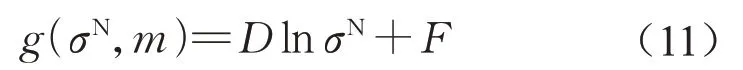
得到恢复率函数后，应根据上述特征对其参数进行定义。如为满足式（8），D应大于0；同时，由于式（10）为单调递减函数，故对应恢复函数系数应满足

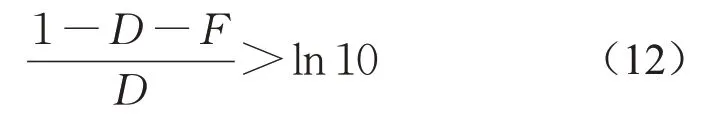
至此，捣固作业恢复率函数形式推导完成。

2.4.2 打磨作业

根据上文所述，线路打磨作业对σN没有影响，主要影响的是作业区段的恶化速率。所以，针对打磨作业的恢复函数，只需改变恶化率函数的相关参数即可。故在完成线路打磨作业后，根据式（7），恶化率函数应变为

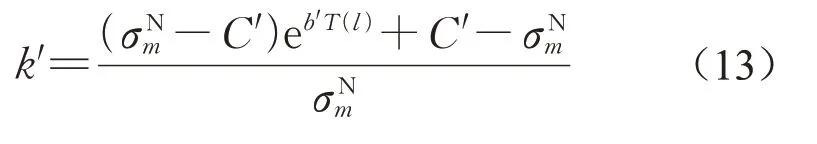
式中：参数b′和C′通过拟合打磨作业后恶化函数得到。

设打磨作业前该区段恶化率为k，原则上来说，对于任意σN，应有k≥k′恒成立。同时打磨后的恶化率也应与打磨后的天数有关，故这里引入变量p，定义变量p为作业区段m距上次线路打磨作业的天数，则恶化率函数k可被重写为

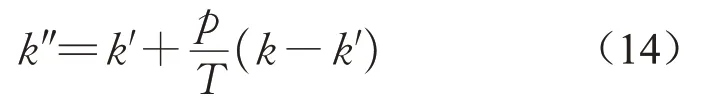
式中：T为区段m进行钢轨打磨作业的周期，d；式（14）中第二项为时间补偿项。

分析式（14）可知，当区段m刚完成线路打磨作业时，p取0，此时恶化率仅由前一项组成，即刚完成打磨作业后的拟合恶化率函数。随着时间的推移，恶化率不断变大，σN恶化量加快。最后，当p=T时，恶化率k″=k，恶化率函数退化为未打磨状态下的恶化率k。至此，完成了打磨作业后恶化率函数的修正。

3 恶化矩阵的建立

所谓恶化矩阵，即直接用于该区段几何不平顺预测计算的矩阵表格，其自变量为轨道几何不平顺值，因变量为打磨作业前后的恶化率，通过该矩阵可以在仅得知目前轨道几何不平顺值后直接得到该区段轨道不平顺的发展规律，方便现场进行轨道不平顺的预测。同时通过上述研究可以发现，对于一个确定的线路区段以及天窗间隔来说，恶化率仅由不平顺值以及是否打磨决定，且可长期保存与调用。根据此特点，可建立长期保存使用的恶化矩阵，并基于恶化矩阵进行轨道几何不平顺的预测，提高预测的适用性以及运算的逻辑性。

矩阵Pm共有3列数据，第一列表示无轨距不平顺值σN，第二列表示线路未经钢轨打磨的恶化率，第三列表示线路在进行钢轨打磨作业后的恶化率。而矩阵Pm一共有行，第i行第一列的取值由下式决定：

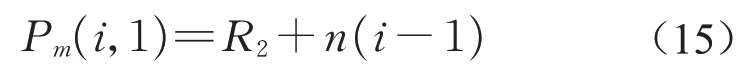
式中：Pm(i，1)的单位为mm，i的取值范围为［1，的取值表示线路在进行钢轨打磨作业前，无轨距不平顺值σN=Pm(i，1)时，此线路作业区段m的恶化率，此时为无轨距TQI的恶化率，其定义与式（4）一致，只需确定无轨距TQI的恶化公式，带入式（7）计算即可，时间跨度为1 d；Pm(i，3)的取值表示线路在进行钢轨打磨作业后，无轨距不平顺值σN=Pm(i，1)时，此线路作业区段m的恶化率，时间跨度为1 d。需要说明的是，此时钢轨打磨作业后的恶化率是由式（13）确定的，并未考虑打磨作业后天数的影响。

在确定了恶化矩阵Pm后，需要明确其运算方法，形成基于恶化矩阵的轨道几何不平顺的预测，具体计算流程如图2所示。

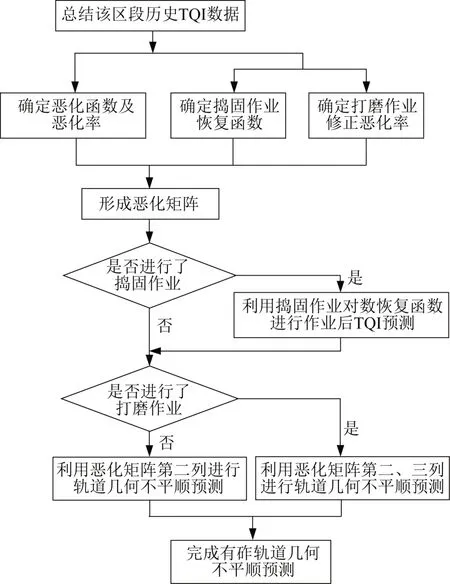
图2 有砟轨道几何不平顺预测流程Fig.2 Flow chart of geometric irregularity prediction of ballasted track

根据图2表述内容，主要运算过程如下：当作业区段m在时间区段l的无轨距不平顺值为σNm，l时，此时对应的恶化矩阵Pm为第行数据，即未经打磨及打磨后的恶化率分别为先不考虑线路捣固作业和钢轨打磨作业对线路恶化的影响。容易得到，该区段在1 d后的无轨距不平顺值为

可将上述操作视为一次函数迭代，为方便表述，将式（16）右侧迭代记为H(σN)。其意义为：区段无轨距不平顺值为σN未经打磨时经过1 d后变化为H(σN)。当迭代j次后有

其中，变量σNm，l的下标既表示为迭代次数，也可理解为恶化天数。那么该区段下一天窗时间的无轨距不平顺值为

根据式（18）就可以得到该区段不经捣固与打磨下一天窗的无轨距的轨道不平顺值。当区段m刚完成线路打磨作业时，恶化率就应采用打磨作业修正后的情况，即恶化矩阵Pm的第三列，那么1 d之后的无轨距不平顺值为

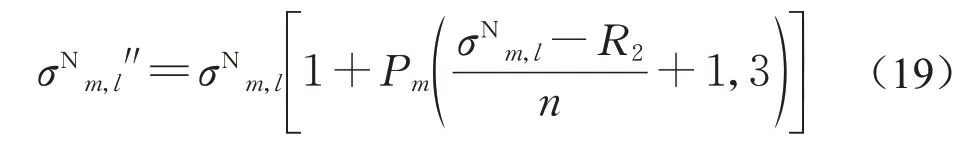
同样参考式（16），将式（19）右侧操作记为L(σN)，其意义为：区段无轨距不平顺值为σN经过打磨1 d后变化为L(σN)，那么该区段在下一天窗时间时轨道不平顺值为

然而式（20）并没有考虑打磨天数对恶化率的影响，为了提高线路打磨作业对线路几何不平顺的影响的预测精度，应对函数H(σN)和函数L(σN)进行修正。由式（14）可知，L(σN)会在一个钢轨打磨周期的时间下衰变为H(σN)，所以修正后的无轨距不平顺值递推公式（不考虑线路捣固作业）如下：

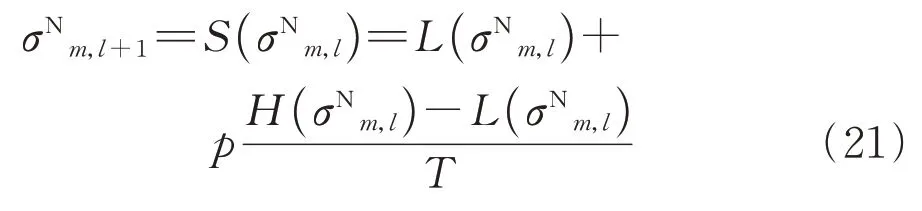
式中：p为作业区段m距离上次钢轨打磨作业的天数；T为作业区段m钢轨打磨作业的周期，d。

为方便说明，将式（21）等式右侧的复合函数视为一个新的函数S(σN)，可以发现，函数S(σN)并未考虑线路捣固作业，参考式（9）捣固作业后的恢复率公式，可得到捣固与打磨复合作业下离散化的无轨距不平顺值递推公式如下：

式中：[x]为高斯向下取整函数，进行取整是为了方便单位统一；Y为mmax×lmax的二维矩阵，Y(i，j)为矩阵Y第i行第j列的取值。矩阵的取值规则如下：

恶化矩阵Pm的取值因仅由此作业区段的恶化函数决定，可作为区段恶化性质作为常数矩阵长期储存，计算时进行调用。

4 实例分析

4.1 恶化函数拟合验证

本节数据来源于京沪铁路上行某里程区段内轨检车数据，对数据进行预处理后，可以得到该里程下TQI随时间变化曲线，如图3所示。

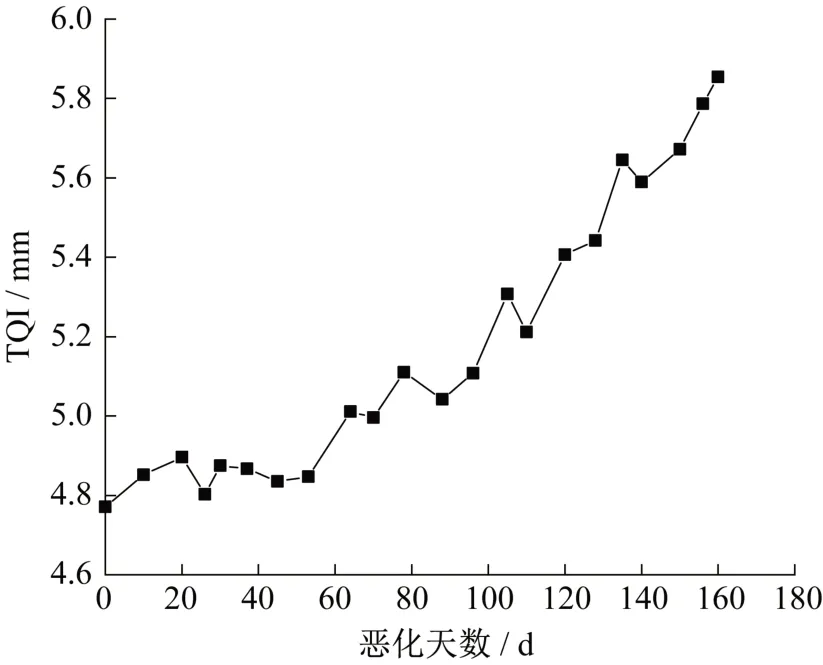
图3 京沪铁路某区段TQI随时间的变化Fig.3 TQI time in a section of Beijing-Shanghai Railway

由图3可知，TQI虽然有一些波动，但整体的趋势是不断变大的，且近乎呈指数函数上涨，TQI的变化率随着TQI的增大而增大。这说明采用指数函数拟合可以较好地反映现场轨道不平顺的变化。拟合得到的TQI变化曲线如图4所示。

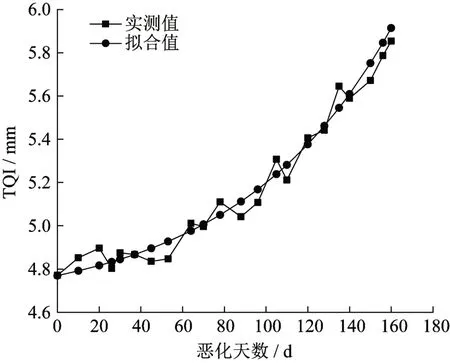
图4 京沪铁路某区段TQI函数拟合Fig.4 TQI function fitting of a section of Beijing Shanghai Railway

拟合函数表达式为

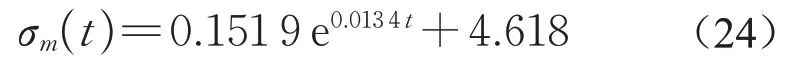
函数表达式与现场数据的相关性为0.974，认为二者高度相关，可以用此函数来描述该区段TQI恶化趋势。说明采用指数函数进行恶化函数的拟合效果较好。

4.2 捣固作业恢复率函数验证

对式（11）建立的捣固作业后的恢复函数进行可靠性验证。本节主要选取了3个有代表性的区段，分别为曲线段、直线段、桥梁段，对模型的预测精度进行验证。数据来源为2015—2019年京沪铁路上行轨检车数据，在进行分析时，去掉了TQI中轨距单项。

以2015—2019年京沪铁路上行直线区段为例，给出这5年中经捣固作业后无轨距TQI变化图，如图5所示。

由图5可以发现，捣固作业后，无轨距TQI有明显的下降，说明捣固作业后恢复函数的假设符合现场实际。为验证捣固作业后对数恢复函数的精度，采用2015—2018年的数据进行拟合，并利用2019年的数据进行预测对比，共选取了曲线段、直线段、桥梁段3个区段。最终的捣固作业前后对比见表1。

图5 2015—2019年某直线区段捣固作业前后无轨距TQI对比Fig.5 Comparison of non-gauge TQI before and after tamping in a straight section from 2015 to 2019

由表1可知，3个区段误差均在7%以内，平均误差为5%，实测值与理论值最大差为0.2 mm，然而对于现场预测轨道不平顺来说，主要需要了解其大致走势及范围，实测值与理论值差距在1.0 mm以内均满足现场要求，这也说明捣固作业后采用对数函数建立恢复率模型可以适用于现场预测。

表1 捣固作业前后无轨距TQI对比Tab.1 Comparison of non-gauge TQI before and after tamping

4.3 复合作业下TQI预测验证

为了更好地验证模型中复合作业下的预测情况，即该区段先进行捣固作业后又进行打磨作业，这里选取2019年京沪铁路某里程区段进行验证。该区段线路在进行捣固作业后全年仅发生了一次打磨作业，没有进行其他大机作业。图6给出该区段进行捣固作业后，打磨作业对无轨距TQI影响走势图。

由图6可知，打磨作业前后无轨距TQI的变化速率出现明显的改变。打磨作业后，TQI变化率较打磨前平缓，说明打磨作业可以降低TQI恶化速率。为验证打磨作业恢复模型的可靠度，以及捣固作业后是否会对打磨作业的预测精度产生影响。需根据第三节所述内容确定恶化矩阵，并根据式（21）进行迭代，得到打磨作业后预测的无轨距TQI。

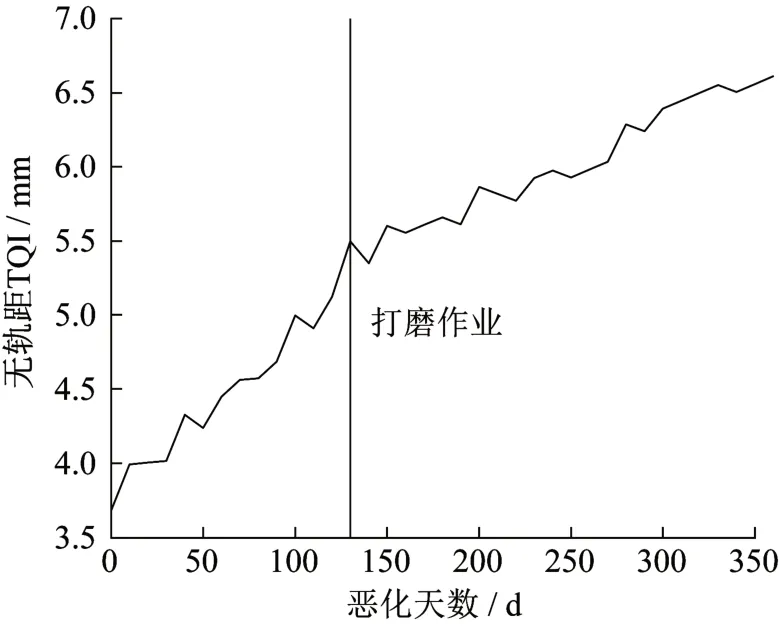
图6 2019年京沪线某区段打磨作业前后无轨距TQI走势Fig.6 Trend of non-gauge TQI before and after grinding operation in a section of Beijing Shanghai Railway in 2019

根据现场实测数据，线路打磨作业前拟合的恶化函数表达式为

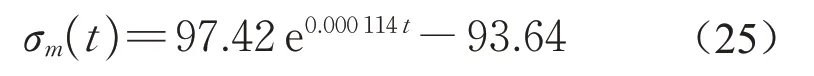
线路打磨作业后拟合的恶化函数表达式为

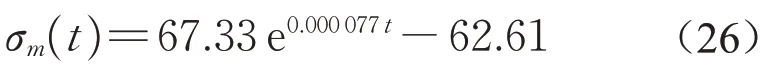
得到了打磨作业前后恶化函数后，即可根据式（7）与式（14）得到恶化矩阵，如表2所示。

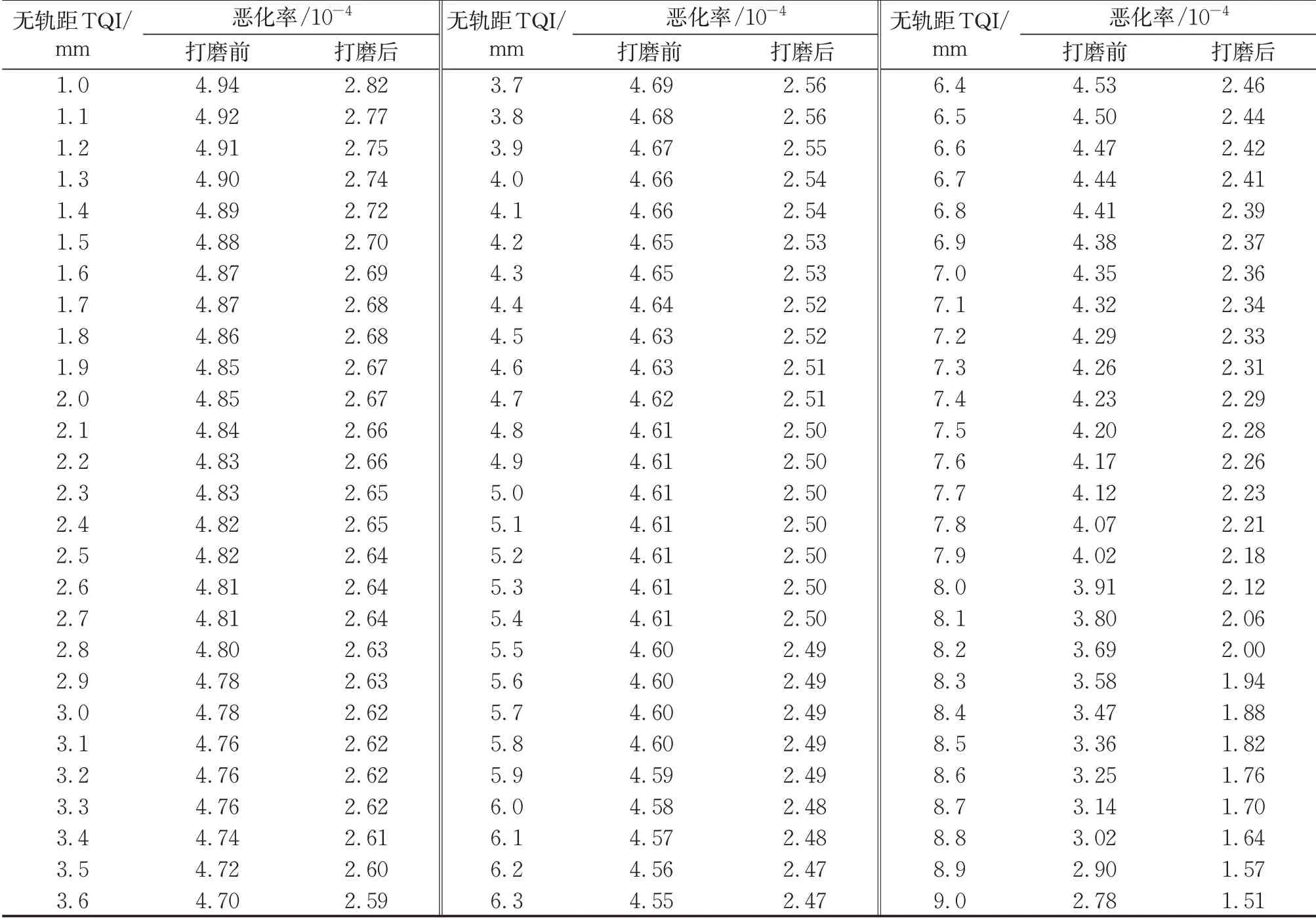
表2 分析区段恶化矩阵Tab.2 Deterioration matrix of analyzed section

在得到了恶化矩阵后，就可以进行打磨作业后无轨距TQI的预测，初始值为进行打磨作业时无轨距TQI，带入式（21）进行迭代，确定打磨后TQI数据。最终得到的打磨后现场实测数据与预测数据对比，如表3所示。

从表3可以看出，打磨作业后的恢复模型可以考虑到恶化速率减缓效果，并能进行合理预测。所建立的有砟轨道几何不平顺预测模型适用性较好、精度较高，平均误差仅为3.1%，实测值与预测值最大差距为0.45 mm，且能够保证一年的有效预测时间，满足现场预测需求；捣固作业后再进行打磨作业对轨道不平顺的预测精度影响较小，模型仍可以进行合理预测。同时现场在对某区段进行捣固作业后，往往会间隔较长时间再进行打磨作业，也确保了在预测时降低两种作业的相互影响。

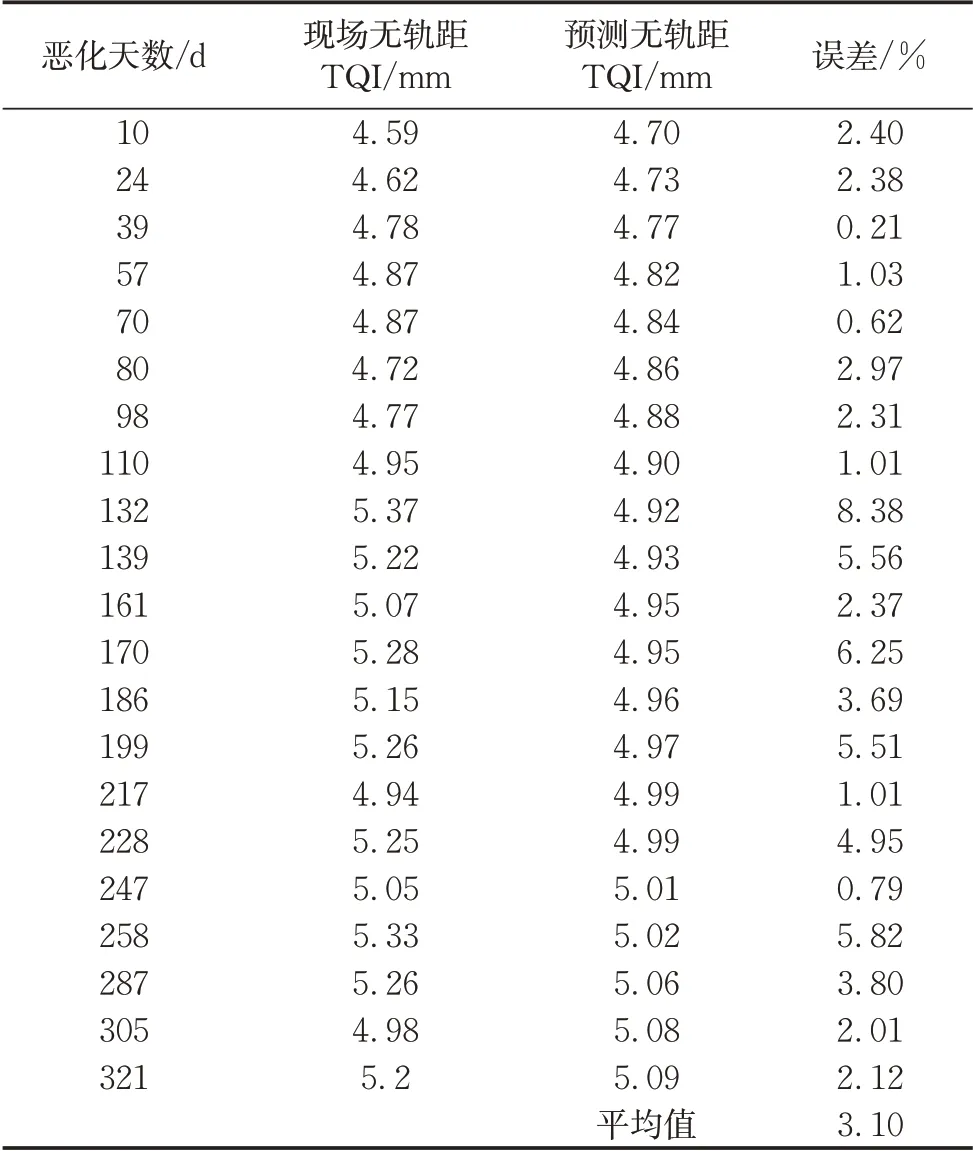
表3 现场数据与预测数据对比Tab.3 Comparison of field data and prediction data

通过上述实例分析说明，建立的恶化模型以及捣固打磨作业后的恢复模型可以很好地适用于现场TQI的预测，预测趋势与实际变化趋势一致，模型可靠度较高；所建立的恶化矩阵方便计算，同时考虑了区段的差异性，预测精度满足需求。

5 结论

本文通过分析轨道几何不平顺变化趋势，建立了有砟轨道几何不平顺恶化模型，定义并推导了适用于现场计算天窗间隔恶化量的恶化率函数；同时考虑捣固与打磨作业对轨道不平顺的影响，建立了捣固与打磨作业下轨道几何不平顺恢复模型；为方便计算，对恶化模型及恢复模型进行整合，建立了恶化矩阵，形成了通过恶化矩阵进行轨道不平顺预测的计算流程；通过京沪线案例分析，说明建立的模型具有适用性，可以较好地预测轨道几何不平顺的变化，精度满足现场预测需求。得到的主要结论如下：

（1）本文在推导恶化函数时，考虑了恶化函数的速率应逐渐增大，最终采用指数函数进行恶化函数拟合；同时推导了以轨道不平顺为自变量的恶化率函数，适用于现场计算天窗间隔内TQI的恶化量。

（2）捣固作业可以降低无轨距的轨道不平顺值，根据捣固作业的特点，为方便计算，最终采用对数函数进行捣固作业前后无轨距的轨道不平顺恢复率的预测；打磨作业可以降低无轨距的轨道不平顺恶化速率，根据打磨作业的特点同时考虑打磨周期的影响，重新修正了打磨作业后的恶化率。

（3）通过恶化函数与恢复函数建立的恶化矩阵方便现场使用，并可进行长期储存调用。利用恶化矩阵的几何不平顺预测模型提高了运算的逻辑性及预测的精度。京沪线的实例分析表明，该模型可以较好地进行现场轨道不平顺值的预测，模型具有一定的可靠性，捣固作业后对打磨作业预测精度的影响较小，复合作业下预测的精度满足现场需求。

本文考虑了捣固与打磨作业对轨道不平顺的影响，针对区段差异性，形成各自独特的恶化矩阵，建立新型有砟轨道几何不平顺预测模型，并与现场实例进行了对比验证。但由于数据有限，没有验证先打磨再捣固对轨道不平顺预测的影响，二者同时作业下式（22）的预测可靠性也需进一步验证。

作者贡献声明：

许玉德：方案制定，资金筹措，过程监督。

吴宣庆：模型确定，数据分析，论文写作。

刘思磊：模型确定，数据分析，论文校正。

薛志强：数据分析，论文校正。

李少铮：数据分析，论文校正。

李长生：资金筹措，论文校正。