考虑到达预测误差的短间距交叉口公交信号优先方法

吴 兵， 王海山， 王艳丽

（同济大学 道路与交通工程教育部重点实验室，上海 201804）

发展公共交通是改善城市交通拥堵的有效途径，但是运行速度较低是近年来地面公交竞争力较低的根本原因之一［1］。高效的公交服务才能提高其竞争力，这需要有效的公交信号优先控制方法［2］。公交信号优先分为被动优先、主动优先和自适应优先3类［3-4］。其中，被动优先虽能适应于流量较大的场景，但是由于其受实时交通状态干扰较大，因此优先成功率低［5-8］；自适应优先虽是理论上最佳的公交信号优先解决办法，但对检测设备以及求解效率的严格要求限制了其广泛投入使用［9-13］；主动优先则在实践中更受欢迎。

主动优先根据公交的实际到达情况，动态地调整信号方案，从而提高优先成功率，以达到降低公交车在信号交叉口延误的目的［14］。主动优先的研究可追溯到1979年［15］，按照优先权强弱可分为无条件的优先和有条件的优先［16］。无条件优先为所有到达的公交车授予优先权，不论公交车辆是否晚点，但未必立即被放行［17］。Ludwick等［18］首次验证了无条件优先的有效性。有条件优先则根据预先设定的阈值条件（如公交车载客人数）判定是否给予公交车优先权［17］。柳祖鹏等［19］提出了基于绿灯需求度的相位切换决策方法。主动优先按照方法复杂度也可分为基于规则的优先和基于模型的优先［16］。Zhou等［20］将公交车到达场景划分为8类，并分别制定优先规则。毋庸置疑，基于规则的优先在相位数量多、关联交叉口多的情况下会非常繁琐，并且不能确保最终执行的信号控制方案是最佳的。Teng等［21］和Liu等［22］提出了考虑多背景协调相位的优先模型和方法。基于模型的优先通过捕捉公交信号优先问题的本质约束，最佳的信号控制方案通过求解所构建的最优化问题得到。

但是，现有方法大多需要提前至少一个信号周期预测［23］公交车到达才能实施优先，此时各个相位的绿灯时长可以以公交信号优先为目标而任意调整。然而，实际中城市道路交叉口间距较短（通常在300～500 m之间），无法满足这一时距要求。特别是对于短间距（＜300 m）交叉口，要实现公交信号优先，就必须在很短的响应时间内（通常不超过30 s）完成对信号方案的调整。目前常用的方法有两种：①信号抢占［23-24］，该方法在交通流较大时负面影响显著，几乎仅用于公交优先级极高，且响应时间极短的场合（如有轨电车轨道与普通道路的交叉口）；②基于规则的公交信号优先，此类方法只能通过同步调整公交到达停止线的时刻及之后的相位的绿灯时间［25-26］，无法考虑调整公交到达停止线的时刻之前的相位的绿灯时间，因而不能充分地均衡分配损失。此外，交通状态和驾驶人个体特征的差异性导致公交车到达停止线的时刻存在预测误差，这进一步限制了当前主动或自适应公交优先的应用与推广［2］。

为了提高公交车的运行速度，进而提高公交竞争力，本文提出了一种可以适用于短间距交叉口、考虑到达预测误差、最大程度地减少对其他车辆影响的主动公交优先控制方法。

1 公交信号优先模型

1.1 模型思路

本文提出的主动公交优先方法以消除公交车在交叉口的停车等候时间为目标，在预测公交车到达停止线的时刻时，以区间估计代替点估计，将短交叉口间距造成的短响应时间问题考虑在模型中。此方法不改变原配时方案的信号周期，以对原配时方案调整幅度最小为准则均衡分配各个相位间的绿灯损失和收益，适用于任意数量相位的原始配时方案。本方法包含公交车到达检测、公交车到达停止线的时刻预测、确定公交相位的候选插入位置、绿灯再分配、方案比选和方案执行6个步骤，如图1所示。

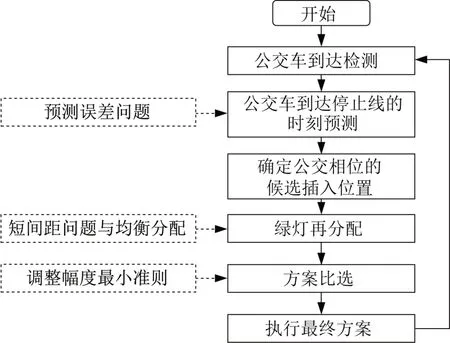
图1 控制方法的流程图Fig.1 Framework of proposed method

1.2 模型假设

本文的模型假设如下：

（1） 公交车运行在公交专用道上。

（2） 公交车到达检测断面与交叉口停止线的距离较短（不超过300 m）。

（3） 在公交车按照期望运行速度运行的条件下，车尾完全进入出口道的时刻之前，公交车享有优先通行权。

（4） 信号周期长度不可改变。

（5） 假设检测断面与停止线之间无公交车站。

1.3 考虑误差的公交车到达时刻预测

路侧传感设施设置在交叉口停止线前一定距离（不超过300 m）处，用来实时获取公交位置、速度以及车身长度等信息。公交车通过检测断面时，路侧传感设施向中央控制单元发起优先通行请求。检测断面与交叉口停止线之间的距离被称为响应距离。图2是交叉口进口道及其检测断面的位置示意图。

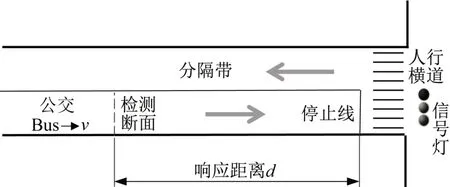
图2 进口道检测断面设置示意图Fig.2 Diagram of road

根据模型假设，公交到达停止线的时刻根据公式（1）计算。

式中：tarrive为预计公交车头不减速抵达停止线的时刻；tdetect为公交车头抵达检测断面的时刻；d为响应距离；v为公交期望运行速度。

为了避免驾驶人在交叉口前因红灯而下意识地减速，考虑到达误差，并结合假设（3），本文认为公交车实际到达停止线的时间区间由tarrive确定，此区间被称为到达窗口，其开始和结束时刻分别用tlower和tupper表示。到达窗口按照公式（2）～（4）确定。显然，在对tarrive的预测误差有充分的了解时，到达窗口的宽度可以设置得更合理。即，当到达窗口过长时，其他方向的车辆的通行效益将受到较大损失；当到达窗口过短时，公交车可能频繁错失优先权。

式中：tlower为到达窗口开始时刻；tupper为到达窗口结束时刻；tpre为前优先持续时间；tpost为后优先持续时间；dcross为公交车来车方向上，交叉口相对的两个进口道停止线间的垂直距离；Lbus为公交车长。

在正态分布假设下，前（后）优先持续时间tpre（tpost）设置为到达时刻估计值tarrive的标准差便可保证公交车以68.27%的概率成功享受优先权。然而，公交车滞后到达停止线的后果更为严重，这意味着公交车需要等候一个周期方可通行，因此tpost可以依据假设（3）设置得更大。显然，tarrive的标准差越小，对社会车辆的影响越小。

1.4 绿灯再分配

绿灯再分配用于均衡分配绿灯增益和损益，可分为预处理、前向分配与后向分配3个子步骤。本文参照分担率γk分配绿灯增益或损益，它是各个相位应承担的绿灯损失或收益之比。分担率可以根据各个相位的绿信比确定，此时绿信比即为分担率。此外，分担率也可以根据关键饱和度或者动态绿灯比确定，此时分担率是关键饱和度或动态绿灯比归一化后的比率。其中动态绿灯比是指到达窗口中，各相位的绿灯时长占到达窗口总时长的比例。

1.4.1 预处理规则

在绿灯再分配之前，为了确保新配时方案与原配时方案的信号周期相同，制定如下5条规则：

（1） 若公交车抵达检测断面时刻tdetect与到达窗口的起止时刻不在同一个信号周期内，且均不在第一相位的绿灯时间内时，将tdetect和第一相位缓冲时间tbuffer，1置为0。

（2）若到达窗口的开始时刻tlower在第一相位的绿灯时间内，则将tlower置为第一相位绿灯阶段的结束时刻tend，1。

（3）若到达窗口始于上一信号周期，终于下一信号周期，则将到达窗口的结束时刻tupper设置为信号周期长度C。

（4）若到达窗口在第一相位绿灯阶段内，则保持原方案不变。

（5）若上述情况均未出现，则直接进入再分配的前向分配和后向分配环节。

预处理场景示意图如图3所示。

图3 预处理场景示意图Fig.3 Schematic diagram of preprocessing scene

1.4.2 前向分配

前向分配是对相序位于公交专用相位之前的相位的绿灯时间的再分配办法，用于解决短交叉口间距造成的短响应时间问题。假设插入的公交相位在调整后的配时方案中为第j个相位，而公交车在第id个相位抵达检测断面，则相位id与相位j之间的各个相位k的可操作时间tavail，k可根据公式（5）计算。

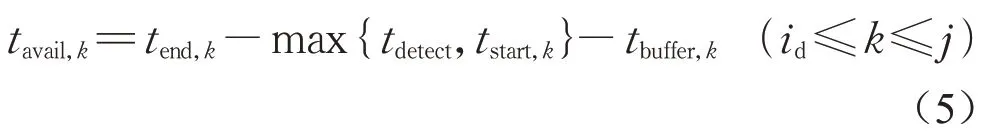
式中：tavail，k为相位k的可操作时间；tstart，k为原方案中相位k的绿初时刻；tend，k为原方案中相位k的绿末时刻；tbuffer，k为相位k的缓冲时间，缓冲时间是出于安全考虑，而在原方案中设定的不可压缩的时间，通常可设置为黄灯时间与全红时间之和。当前在显示的相位至少经过缓冲时间后才可以切换到下一相位，缓冲时间的存在同时也保证了信号灯倒计时的可实施性。

本文假设路侧检测设施的响应距离不超过300 m，因此绿灯再分配时应考虑各相位实际损失承受能力的差异性。调整后的配时方案中各相位绿灯时长按照公式（6）～（8）计算。

当tavail，k小于或等于0时说明相位k已经不能承担损失，否则应尽量足额承担预期损益或增益。

前向分配虽然是为短间距交叉口设计的，但它同样适用于长间距交叉口。适用于长间距交叉口的公交信号优先方法的一个关键假设为各个相位的绿灯时长可以任意调整。当交叉口间距较长时，公交车被检测到的时刻tdetect不会与到达窗口的起止时刻（tlower和tupper）在同一周期内。根据预处理规则（1），tdetect被置为0，此时公式（5）中的第二项总是取值为tstart，k，那么tavail，k取值总是为正，这意味着各个相位的绿灯时长可以任意压缩；此外，由公式（7）可知，恒为正数的tavail，k确保了tdue，k非负，那么t~due，k便可以取值为负数，这意味着所有相位的绿灯时间可以任意延长。而tbuffer，k则可类比为最短绿灯约束。因此本方法适用于长间距交叉口。

此外，在极端情况下（响应时间或距离为0时），本方法仍然适用，此时本方法将退化为信号抢占［23-24］。

1.4.3 后向分配

后向分配是对相序位于公交专用相位之后的相位的绿灯时间的再分配办法，位于公交专用相位后的每一个相位m的绿灯时间按照公式（9）计算。

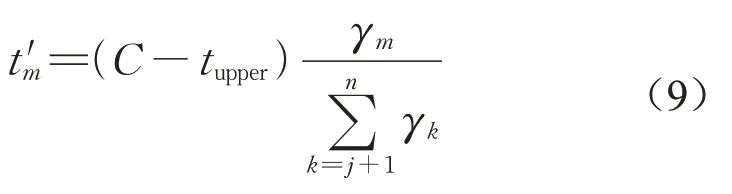
式中：C为信号周期长度；γm为相位m的分担率；γk为相位k的分担率；t′m为调整后相位m的绿灯时长；j为公交相位的插入位置。

黄灯时间和全红时间可以纳入缓冲时间内，并在方案比选完成后，从绿灯时长中剥离。绿灯再分配后，所有候选方案组成的集合S称为候选方案集。

1.5 评价指标与方案比选

1.5.1 评价指标

调整幅度被选作比选方案的评价指标，调整幅度用各个非公交专用相位的绿灯时间的相对变化量的平方和来计算，调整幅度越大表明扰动越大，相关方案越不应该被采用［27-28］。绿灯时长相对变化量与调整幅度按照公式（10）～（11）确定。

式中：dk为相位k的绿灯时长相对变化量；Δ为调整幅度。

1.5.2 方案比选

最终的配时方案按照公式（12）确定。

2 有效性分析

2.1 仿真场景

本文以位于上海市嘉定区的沪宜公路与洪德路交叉口为例搭建仿真场景测试方法的有效性。该交叉口应用了SCATS （Sydney Coordinated Adaptive Traffic System）系统，采用三相位控制模式，未实施公交信号优先。沪宜公路为双向6车道，洪德路东段为双向2车道，西段为双向3车道，如图4所示。沪宜公路两侧均设有公交专用道，上下游交叉口与此交叉口的间距均约为200 m，检测断面距离停止线180 m。仿真基于Python利用VISSIM 7的COM接口实现，VISSIM 7在仿真结束后生成的评价文件将用于后续结果分析。

图4 沪宜公路与洪德路交叉口示意图Fig.4 Schematic diagram of intersection of Huyi Highway and Hongde Road

2.2 数据采集及说明

为了测试方法的有效性，采用现场实地采集的流量、速度以及配时数据进行仿真，数据采集时段为18：00—19：00，如表1所示；现状信号配时方案如表2所示，南北方向关键饱和度约为0.47；上下行的公交车发车间隔均为300 s；公交车的平均运行速度为31 km·h-1。沪宜公路上，此交叉口的两个相邻交叉口的饱和度分别为0.47和0.53，交通条件较好，因此仿真时未考虑二者的影响。

表1 沪宜公路与洪德路交叉口的高峰小时流量Tab.1 Rush hour flow at intersection of Huyi Highway and Hongde Road

表2 沪宜公路与洪德路交叉口的现状信号配时方案Tab.2 Background signal timing plan for intersection of Huyi Highway and Hongde Road

2.3 实验方案

为了通过对比分析本研究方法的有效性，本文额外设计了3种对照控制方法。第一种仅采用常规无公交优先的信号控制，即现状；第二种应用常规信号优先（CTSP）；第三种与本研究方法一样使用绿信比作为分担率，但不考虑预测误差；第四种为本研究方法。基于长预测窗口的信号优先方法在有效性实验中不予考虑，详细实验方案设计如表3所示。VISSIM仿真实验中到达误差的分布信息可通过预实验获取，实际应用中可以根据历史数据估算。

表3 有效性实验设计Tab.3 Design of effectiveness experiment

2.4 实验结果

有效性实验的结果如图5所示。相比于无优先方案，3种优先方法均能一定程度降低人均延误、优先方向车均延误以及公交平均延误，本研究方法几乎消除了公交车延误。相比于常规优先，后两种方法将交叉口人均延误进一步降低了11.4% 和24.3%，并且没有以显著提高非优先方向车均延误为代价。考虑预测误差后，公交平均延误进一步降低了77.9%，这是因为到达预测误差信息能够指定更为精准的到达窗口，公交车成功享受优先权的几率提高了。相比于不考虑预测误差的方法而言，本方法虽然略微提高了优先方向的车均延误，但是非优先方向的车均延误以及整个交叉口的人均延误却呈现下降趋势，表明将预测误差以及均衡分配理念考虑在内是对整个交叉口有益的。

图5 有效性实验结果Fig.5 Results of effectiveness experiment

3 适用性分析

3.1 “恶劣条件”下仿真场景

当各个方向的流量差异悬殊时，人均延误或车均延误并不能公平地评价控制方法的实施效果。当各个方向的流量、饱和度、绿信比均相近时，任何一个方向相对其他方向都不是无足轻重的，即便是十分微小的分配不均都将对方法的实施效果产生显著影响。本文设计了另一测试交叉口用于验证其在“恶劣条件”下的适用性。测试交叉口4个进口道均为双向8车道，如图6所示，采用四位控制模式，东西方向设有公交专用道，在距离停止线240 m处设有路侧传感设施。

图6 适用性实验测试交叉口Fig.6 Schematic diagram of validation intersection

3.2 “恶劣条件”下实验方案

适用性实验将在这种“恶劣条件”下探索信号周期、流量、公交车期望运行速度对实施效果的影响，每组参数重复实验5次，每次仿真持续3 600 s，实验的参数设定如表4所示。其中，饱和度、信号周期长度以及公交期望运行速度均涵盖了各种典型取值，300 s的公交发车间隔则足以消除上一次优先造成的负面影响，tpre采用一倍到达预测标准差（2 s），到达预测标准差根据仿真预实验确定，实际应用中可以根据历史数据估算。其中饱和度、信号周期长度和公交期望运行速度的实验步长分别为0.05，40 s和2.5 km·h-1。

表4 实验参数设置Tab.4 Setting of experimental parameters

适用性实验使用平衡载客比率作为评价准则。载客比率是公交平均载客人数和社会车辆平均载客人数之比。平衡载客比率则是指，当人均延误相等时，待评测方法与无优先方法的载客比率之比。当实际载客比率高于平衡载客比率时，采用待评测方法可降低人均延误。

3.3 “恶劣条件”下实验结果

适用性实验的结果如图7所示。公交车期望运行速度与实际运行速度之间的关系如图7a所示，由于驾驶人在通过交叉口时会下意识地降低车速，因此实际运行速度总是略低于期望运行速度，且期望运行速度越大时差异越显著，表明公交车高速运行时绿灯应提前更久亮起，而在原始配时方案下，由于需要停车等候，实际公交车运行速度几乎与期望运行速度无关。

图7b表明公交车的期望运行速度对人均延误没有显著影响，应用此方法后，公交管理部门可以根据道路实际情况，在保证安全的前提下设定尽可能大的期望运行速度，从而提高公交出行方式的竞争力。

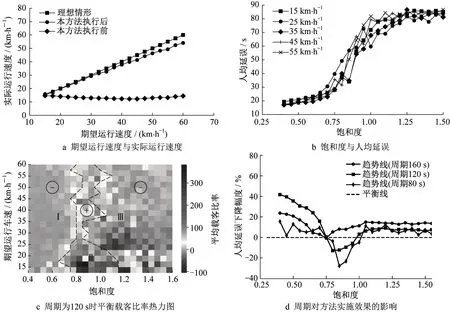
图7 适用性实验结果Fig.7 Results of applicability experiment

图7c是本文所述方法的平衡载客比率的热力图。图中的两条平衡载客比率为40的等高线将热力图划分为3个区域。Ⅰ区表明在交通流量较低时，极易达到平衡条件，此时应大力推广。Ⅱ区表明在近饱和时（饱和度约0.8）需要较高的公交车载客人数才能达到平衡，因此本方法适用于饱和度不超过0.8的信号交叉口。特别地，在公交期望运行速度很低时，平衡载客比率最大值已超过300，考虑到实际载客比率难以高于300，表明此时公交优先权是建立在显著牺牲总通行效率之上的。Ⅲ区平衡载客率大面积表现为负值，且颜色较深，这主要是因为此时产生了严重拥堵，VISSIM只给出了完整通过交叉口的车辆的延误，而大量没有完整通过交叉口的车辆的延误没有被考虑在内，故本文所述方法并不适用。

图7d是期望运行速度为30 km·h-1时，不同周期的原始配时方案条件下，方法实施前后的人均延误下降幅度示意图。从图7d可以看出，实施效果在近饱和区域内会出现明显的下降，而后逐步回升，出于和图7c中Ⅲ区相同的原因，本方法在过饱和场景下并不适用。由于此实验中绿信比不随周期长度变化而变化，当周期较长时，公交信号优先对交叉口通行能力造成的损失更低，因此在交叉口近饱和时应搭配更长的信号周期使用。

4 结论

为了提高公交竞争力，本文以消除公交车在交叉口的停车等候时间为目标，提出了一种面向短间距交叉口，考虑公交车到达停止线的时刻的预测误差，以对原配时方案调整幅度最小为准则，均衡分配各个相位间的绿灯损失和收益的主动优先方法，并设计仿真实验验证了此方法的有效性和适用性。

有效性实验中对比了无信号优先控制和包括本文所述方法在内的3种优先方法的效果，位于上海市嘉定区的沪宜公路与洪德路交叉口被选作仿真分析案例。实验结果表明本文所述方法将公交车在交叉口的等候时间降低了90.8%，大幅度降低人均延误，同时并没有以显著提高非优先方向车均延误为代价。相比常规优先和不考虑预测误差的优先方法，本文所述方法能够进一步降低人均延误、非优先方向的车均延误和公交平均交叉口等候时间，表明在短间距交叉口应用场景下，将预测误差以及均衡分配理念考虑在模型中是全局有益的。

适用性实验分析了本方法在“恶劣条件”下的适用性。实验结果表明，本方法适用于饱和度不超过0.8的信号控制交叉口。此外，公交车的期望运行速度不会显著影响交叉口人均延误，因而公交管理部门可以根据道路实际情况，在保证安全的前提下设定尽可能大的期望运行速度，从而提高公交出行方式的竞争力。

然而，本文没有考虑公交车发车频率较高的情景，当同一周期内有多辆公交车请求优先时，只有先到的公交车能够获得优先通行权，而且本文没有考虑相邻交叉口、公交车站以及实时交通条件演变对公交信号优先造成的影响。本文仅利用到达时刻的预测误差信息提高方法的鲁棒性，如何消除预测误差带来的负面影响有待进一步研究。

作者贡献声明：

吴 兵： 研究概念生成，实验方法设计，论文审阅与修订。

王海山： 研究概念生成，实际调查研究，实验方法设计与结果分析，论文手稿撰写，实验结果可视化。

王艳丽： 研究概念生成，实际调查研究，实验方法设计与结果分析，论文审阅与修订。