一种矩阵块间提前切换的脉动阵列优化策略*
鞠 鑫,曹亚松,文 梅,汪 志,冯 静
(国防科技大学计算机学院,湖南 长沙 410073)
1 引言
最近十多年里,深度学习驱动人工智能经历了一场学术和工业复兴,深度神经网络DNN(Deep Nural Network)极大地推进了计算机视觉、图像处理、语音识别等应用的发展,并交叉融合在众多应用和学科领域中[1,2]。其中,递归神经网络、长期短期记忆和卷积神经网络占据了95%的数据中心需求[3],而这3种类型的神经网络通常都是转化为通用矩阵乘进行运算[4 - 7]。
在提出的所有DNN加速器体系结构中,脉动阵列SA(Systolic Array)因为其操作数的移动仅出现在相邻2个PE(Processing Element)之间,使得其结构规整、控制简单并且可以提供极高的计算密度,从而在工业界(例如Google TPU ASIC[3]、Xilinx FPGA overlays xDNN[8])和学术界[9]被广泛采用。
在脉动阵列执行矩阵乘运算时,片上缓冲通常不足以存放完整的输入矩阵,因此需要在片下对其进行分块。脉动阵列大都会采用片上双缓冲的结构,使脉动阵列的数据准备没有气泡。而对于加载到片上缓冲的矩阵,需要根据脉动阵列的PE行/列数自动分块,并且在运行过程中频繁地进行片上块间矩阵的切换。
传统的脉动阵列单周期输入的数据量通常为2O(O为脉动阵列的PE行/列数),输出的数据量通常为O。数据进入脉动阵列后按照一定的方向流动,因此在填满SA和清空SA的过程中会出现一定的流水线启动和排空开销,且与MAC单元(Multiply ACcumulate unit)延时正相关。对于支持训练的脉动阵列加速器,为了保证精度往往会采用支持浮点运算的MAC单元,其计算延迟通常在4~6个周期[10,11],脉动阵列流水线的启动和排空开销较大。并且现有的脉动阵列总是在完成了当前片上分块矩阵的计算后才切换至下一分块矩阵,在运行过程中会频繁地出现大量PE空闲,导致PE利用率低下。因此,对于支持浮点运算的高性能脉动阵列,如何隐藏脉动阵列的启动和排空开销显得尤为重要。
文献[12]分析了不同映射规则下SA的计算延时,并通过增加PE之间的连线,在一定程度上减少了SA的填充与排空延时,但其控制相当复杂,丢失了脉动阵列结构和控制简单的特性,硬件难以实现。文献[13]在不改变PE间连线的前提下,在PE内部增加了一套缓冲和MAC单元,以提前加载和计算下一个矩阵分块,从而缩短SA计算延时,同时将PE数目减少一半,使总面积几乎不变。这表面上提高了PE利用率,但其缓存和计算资源的浪费并没有得到缓解。
本文针对上述问题,首先分析了一种自然的优化策略:基于双缓冲结构的设计思想,在PE内部设置2套用来存放静态矩阵的寄存器。这种基础双寄存器脉动阵列结构,可以隐藏静态矩阵的加载延时,但在排空脉动阵列时仍然存在大量的PE空闲。
通过对脉动阵列数据流进行建模,本文分析与计算了不同场景下2个分块矩阵间切换的最短时间间隔,提出了一种矩阵块间提前切换的策略,可以减少块间矩阵切换时空闲PE的数量。为了验证该策略,本文实现了一个特定脉动阵列的RTL设计,并在真实的应用负载下进行了测试。测试结果表明,该策略在现有脉动阵列基础上的硬件改动极小,增加的面积开销几乎可以忽略不计,却能在所有场景中得到显著的性能提升。提升的效率与矩阵运算的规模相关,对于典型的AI网络模型(例如AlexNet,ResNet50),一组片下分块矩阵的计算延时可以缩短3 472~29 169个周期,PE利用率可以提升2.56%~33.43%。
2 背景
脉动阵列是一种由O行、O列PE组成的二维阵列,相邻的PE之间相互连接,用于数据传递,如图1中灰色阴影所示。其中,每个PE中又包含1个寄存器,用于存放静态矩阵,和1个计算延时为R的MAC单元,用于乘加运算。
SA执行通用矩阵乘运算Y=AB+C时,共有3种数据流结构[14]:静态矩阵IS(Input Stationary),即A;静态矩阵WS(Weight Stationary),即B;静态矩阵OS(Output Stationary),即C。脉动阵列的性能和能效由数据流结构、脉动阵列的参数(例如PE数量、MAC延时)和输入矩阵规模共同决定[14]。对于MAC延时大于1的脉动阵列,OS的设计复杂且效率低,本文不予讨论。WS因为对B矩阵的高效复用而被现代处理器广泛采用[3],因此本文以WS为例进行分析,但其结论对IS同样适用。
2.1 片下分块
由于片上存储资源有限,需要在片下对输入矩阵进行分块,然后将分块矩阵搬移到片上参与运算,如图1所示。其中,A-offchip规模为M×K,按m行k列进行分块;B-offchip规模为K×N,按k行n列进行分块;C-offchip规模为M×N,按m行n列进行分块。虚线方框表示第1组搬移到片上缓冲参与运算的片下分块矩阵A-onchip、B-onchip和C-onchip,后文分别用A、B、C表示。
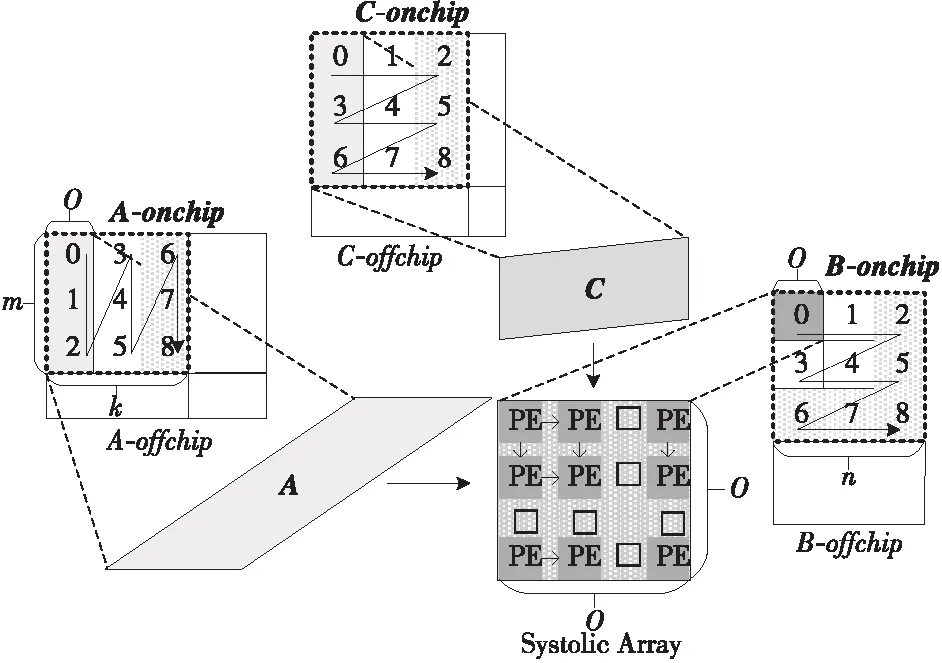
Figure 1 Diagram of block calculation 图1 SA分块计算示意图
2.2 片上分块
以Ai、Bi、Ci和Yi分别表示A、B、C和Y矩阵第i次参与计算的分块,mi×ki和ki×ni分别表示Ai和Bi的规模,mi×ni表示Ci和Yi的规模。Yi的中间结果更新至Ci中,Ci的最后一次计算结果即为Yi的最终结果,运算过程如式(1)所示:
(1)
2.3 PE内部双寄存器基础实现方案
由式(1)可知,在计算片上分块Y=AB+C的过程中,会频繁地进行块间矩阵的切换,从而出现大量的SA填充和排空开销,造成PE资源的浪费。
在块间矩阵的切换过程中,首先加载下一块静态矩阵Bi+1,此时会产生ki+1个周期的静态矩阵加载延时,同时动态矩阵流入必须等待静态矩阵加载完成,所以本文考虑如何提前加载静态矩阵。
原始的PE内部结构如图2a所示,包含1个用于存放矩阵Bi的寄存器和1个MAC单元。基于双缓冲的设计思想,本文在PE内部设置2套寄存器,用于存放Bi和Bi+1,如图2b所示。相比于原始设计,只增加了1个寄存器、 1个多路分配器DMUX(Demultiplexer)和一个数据选择器MUX(Multiplexer),使得每一次分块的切换时刻可以提前Ti+1个周期。

Figure 2 Internal structure of PE图2 PE内部结构
2.4 基础双寄存器脉动阵列中的数据流动分析
m=1,k=3,n=12,O=4,R=2时,SA的数据流动过程如图3所示。0周期开始加载静态矩阵B0到B_REG0;3个周期后B0加载完成,开始加载静态矩阵B1到B_REG1,并分别从左至右和从上至下加载动态矩阵A0和C0;周期6B1加载完成;周期8A0全部进入SA;周期13Y0计算完成并流出SA,然后开始加载静态矩阵B2到B_REG0,并加载动态矩阵A1和C1;周期23Y1计算完成并流出SA,然后加载动态矩阵A2和C2;周期33Y2计算完成并流出SA。其平均PE利用率仅为6.61%。
其计算时空图如图4a所示,横坐标为周期T,纵坐标为行PE,tBi表示静态矩阵Bi的加载周期数,tCi表示动态矩阵Ci第1行的第1个元素完成运算的周期数,tYi表示动态矩阵Ci第1行的第1个元素完成运算到流出SA的周期数,tni表示动态矩阵Ci的最后一行元素完成运算到流出SA的周期数。此例中,各周期数的计算分别如式(2)~式(6)所示:
tB0=tB1=tB2=k=3
(2)
tC0=tC1=tC2=R×k=2×3=6
(3)
tY0=tY1=tY2=O-k=4-3=1
(4)
tn0=tn1=tn2=O-1=3
(5)
t=3×(tC0+tY0+tn0)+tB0=33
(6)
由图4a可知,在矩阵B载入SA和矩阵Y流出SA的过程中,存在大量的空闲PE。基于SA的全流水特性,矩阵B2可以在第10个周期开始进入SA,在第12个周期B0使用完毕,同时B2加载完成;A1和C1可以在B1加载完成后一个周期(第7个周期)流入SA,同理;A2和C2也可以在B2加载完成后一个周期(第13个周期)流入SA,如图4b所示,此种情况下完成计算仅需要24个周期,PE利用率由6.61%提升至9.37%。
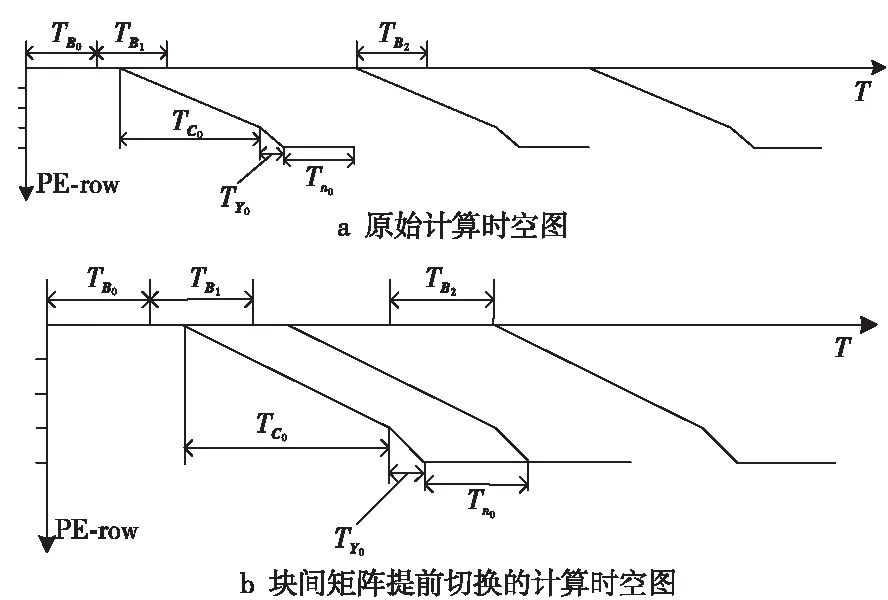
Figure 4 Computational spatiotemporal graph of SA when m=1,k=3,n=12,O=4,R=2图4 m=1,k=3,n=12,O=4,R=2时SA的计算时空图
3 块间矩阵提前切换策略
3.1 静态矩阵提前加载
由于本文在PE中配置了2套寄存器,相邻2个静态矩阵分块Bi和Bi+1会分别加载到2个缓冲中,因此只需要关注Bi和Bi+2之间的切换时机,使得Bi+2加载到SA时不会影响到当前矩阵Yi的计算。
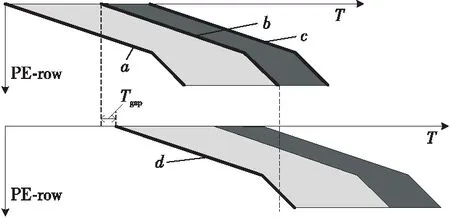
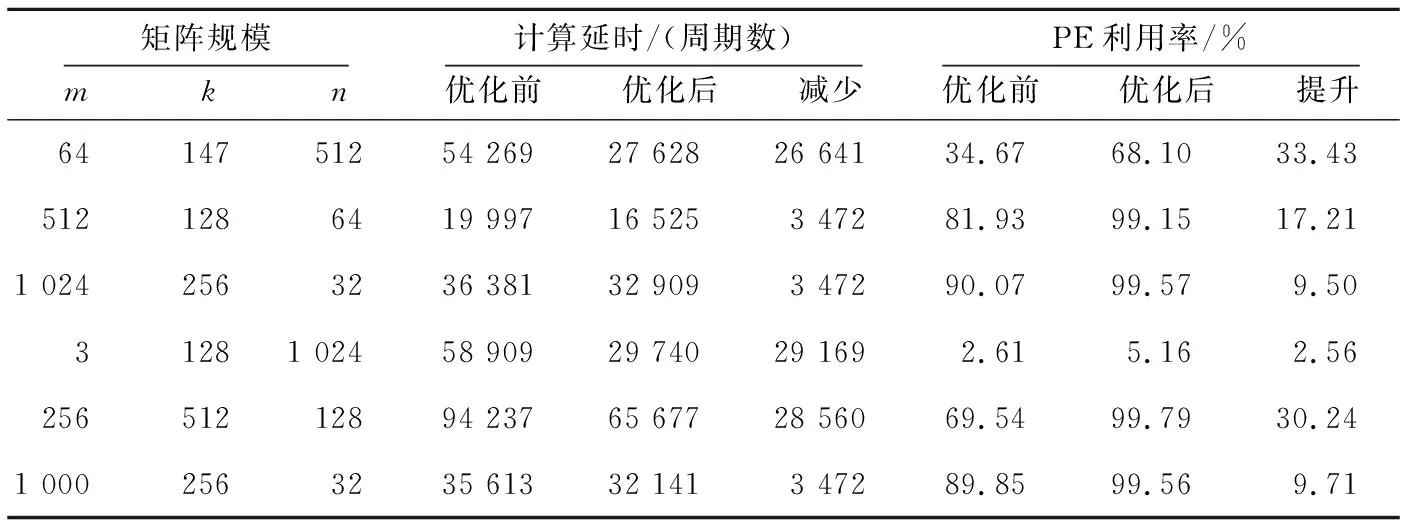
根据ki和ki+2的大小关系可以分3种情况讨论,即ki+2=ki,ki+2>ki和ki+2 Figure 5 Loading timing of static matrix Bi+2图5 静态矩阵Bi+2的加载时机 (1)ki+2=ki。 对于ki+2=ki的情况,如图5a所示,Bi+2在TP之后完成加载则不会影响到Yi的计算,所以Bi+2的加载起始时间为TP-ki+2,等于TP-ki。 (2)ki+2>ki。 对于ki+2>ki的情况,如图5b所示,Bi+2也是在TP后可以完成加载,所以Bi+2的加载起始时间也为TP-ki+2,但小于TP-ki。 (3)ki+2 对于ki+2 综上所述,静态矩阵Bi+2可以开始加载的时刻由式(7)计算: (7) 同时,由于ki+2>ki和ki+2 TBi+2=R×(ki-1)+ni-ki (8) T′Bi+2=R×(ki-1)+ni (9) 基于SA的全流水机制,下一矩阵Yi+1的计算不用等到当前块Yi完全流出SA,而可以在动态矩阵Ai+1和Ci+1准备完成后提前进入SA参与运算,前提是要保证静态矩阵Bi+1加载完毕,并且Yi+1在流出SA的时候不与Yi冲突。类似地,根据ki+1和ki的大小关系,可分为以下3种情况讨论: (1)ki+1=ki。 对于ki+1=ki的情况,Yi+1与Yi的对应元素在SA中流过的周期完全相同,所以只要静态矩阵准备完成后,第i+1块动态矩阵可以紧跟第i块动态矩阵流入SA。如图6所示,图的上、下2部分分别表示Yi和Yi+1的计算过程。其中,折线a表示动态矩阵C第1行的第1个元素流过SA第1列PE的过程,折线b表示动态矩阵C最后1行的第1个元素流过SA第1列PE的过程,折线c表示动态矩阵C最后1行的最后1个元素流过SA第n列PE的过程。第i+1块动态矩阵在第i块动态矩阵的下一个周期流入SA,其计算结果Yi+1也会在Yi后一个周期顺序流出SA,此时第i+1块动态矩阵的末行与第i块动态矩阵的首行流入SA的间隔Tgap=1。 不难发现,只要保证动态矩阵Ci+1第1行的第1个元素流过SA第1列PE的过程中不与动态矩阵Ci最后1行的第1个元素冲突,整个矩阵分块都不会冲突,因此后文只关注动态矩阵Ci最后1行的第1个元素(图6中的折线b,后图用虚线表示)和动态矩阵Ci+1第1行的第1个元素(图6中的折线d,后图用点画线表示)在SA中第1列PE中的使用情况。 Figure 6 Inflow timing of the i+1-th dynamic matrix when ki+1=ki图6 ki+1=ki时第i+1块动态矩阵的流入时机 (2)ki+1>ki。 对于ki+1>ki的情况,Yi+1的计算延时大于Yi的计算延时,所以第i+1块动态矩阵可以紧跟第i块动态矩阵进入SA,此时Tgap=1,如图7所示。 Figure 7 Inflow timing of the i+1-th dynamic matrix when ki+1>ki图7 ki+1>ki时第i+1块动态矩阵的流入时机 (3)ki+1 对于ki+1 所以,第i+1块动态矩阵与第i块动态矩阵的最小加载间隙Tgap由式(10)计算。类似地,对于基础双寄存器脉动阵列,其加载间隙T′gap由式(11)计算。 (10) T′gap=(R-1)×ki+O+ni (11) Figure 8 Inflow timing of the i+1-th dynamic matrix when ki+1 为了评估提出的基于脉动阵列的矩阵块间提前切换策略,本文实现了RTL设计,并与现有的脉动阵列进行了比较。出于实现复杂度考虑,本文实现的脉动阵列PE规模为16×16,每个PE中MAC的计算延时为6,数据流采用WS,A、B、C的片上双缓冲大小分别为2×3 MB、2×1 MB、2×256 KB。同时,为了简化设计,静态矩阵Bi+2与Bi的加载时刻采用式(8)计算获取。 在真实的应用负载下,M并不总是很大,K和N也并非总是O的整数倍。因此,为了涵盖尽可能多的情况,即使评估结果更具有说服力,本节将人为生成一些负载规模,包括各种边界情况,即使真实的应用负载即使没有被完全模拟,也能在其中找到适配的场景。 本文令m取1,16,32,64,128,256和512。k分别取113,127和128:k=113时,B矩阵的最后1个行分块只有1行,SA中有15行PE空闲;k=127时,B矩阵的最后1个行分块有15行,SA中只有最后1行PE空闲;k=128时,没有PE空闲。n固定为64,使每一个矩阵分块都能填满SA的每一列。 图9a~图9c分别为k=113,127,128时SA优化前后的PE利用率与m的关系。其中,横轴为m,主纵轴为PE利用率,次纵轴为优化后提升的PE利用率。 Figure 9 Relationship between PE utilization and m before and after SA optimization图9 SA优化前后的PE利用率与m的关系 由图9可知,在m、n不变的情况下,k越接近O的整数倍,PE利用率越高。在k、n不变的情况下,PE利用率随m单调递增,但优化后提升的PE利用率随m先增后减,并在m=128时达到最大:k=113时为36.54%,k=127时为43.06%,k=128为43.54%。 4.2.1 工作负载 表1为几种常见神经网络的部分层参数,其中i_ch表示输入通道数,o_ch表示输出通道数,img表示输入图像尺寸,ksize表示卷积核尺寸,p表示填充尺寸,s表示滑动步长。 由于片上缓存容量的限制,表1中的真实负载都需要在片下提前分块,然后在片上计算分块结果。只要片下分块的m、k、n不超过片上缓冲大小都是合法的,因此允许的分块规模有M×K×N种,但为了充分利用SA的计算资源,本文给出以下分块建议: (1)分块应该尽量均匀,使负载均衡; (2)m应该尽可能大,以提高B矩阵的复用率; (3)k、n尽量接近O的整数倍,减少块内计算时的PE空闲。 基于上述分块原则,表1最后1列给出网络对应的推荐分块规模。 4.2.2 性能分析 优化前后表1中推荐分块的性能对比如表2所示,包括优化前后的计算延时及优化后减少的计算延时,优化前后的PE利用率及优化后PE利用率的提升。 Table 1 Parameters of common network and size of recommended blocks 由表2可知,在m足够大的情况下,优化减少的延时只与静态矩阵的片上自动分块数相关,继续增加m,优化减少的延时不再变化,提升的PE利用率略有下降,但PE利用率更接近100%。减少的计算延时在3 472~29 169个周期,提升的PE利用率在2.56%~33.43%。 Table 2 Performance comparison under load in table 1 before and after optimization 本文在ASAP7[16]工艺下对RTL进行了逻辑综合和功耗评估,时钟周期为0.35 ns,输入输出延时为0.1 ns,加上预留的30%后端布局布线延时,实现的时钟主频不低于2 GHz。优化前后的面积/功耗如表3所示。 由表3可知,提出的优化设计的面积和功耗与基础双寄存器设计的都非常接近。而相比于原设计,单个PE面积增加了0.6%,功耗增加了2.5%;切换控制面积减少了0.2%,功耗降低了0.9%;整体面积增加了0.4%,功耗增加了1.4%。 Table 3 Area/power comparison before and after optimization 4.4.1 性能提升 虽然本文的实验只评估了一个特定的脉动阵列,但本文提出的策略可以适用于任何参数的脉动阵列。并且根据脉动阵列PE间的数据流动特性,对于规模大、MAC延时长的脉动阵列,其性能提升会更显著。因为随着SA规模的扩大,静态矩阵加载周期变长;MAC延时越大,流水线填充和排空的延时越长。 4.4.2 硬件开销 本文策略涉及的硬件改动包括2个方面:PE外静态矩阵加载和动态矩阵流入时刻的计算;PE内增加了1个寄存器和2个数据控制器。 对于前者,由于提出的策略需要的参数比原设计更少,实现面积略有降低;对于后者,虽然硬件开销和PE的个数线性正相关,但对于单个PE而言增加的面积很小,所以即使对于大规模的脉动阵列,其硬件开销也不会剧烈增加。因此,本文提出的策略具有很好的可扩展性。 本文针对脉动阵列矩阵块间切换不及时导致计算过程中频繁出现大量PE空闲,资源利用率不高的问题,提出了一种矩阵块间提前切换的脉动阵列优化策略。该策略能够最大程度地将下一组分块矩阵的流入延时隐藏在当前组分块矩阵的计算过程中,减少矩阵块间切换时PE空闲的数量,提高脉动阵列性能。实验结果表明,优化后的脉动阵列面积仅增加了0.4%,功耗增加了1.4%,但其性能在所有场景中均得到了显著提升。在测试的规模中,当m=k=128,n=64时提升的PE利用率达到最高,为43.54%。同时需要注意的是,本文提到的脉动阵列虽然是正方形的,但本文提出的策略对于长方形的脉动阵列也同样适用。

3.2 动态矩阵提前加载


4 实验及结果分析
4.1 实验负载下的PE利用率
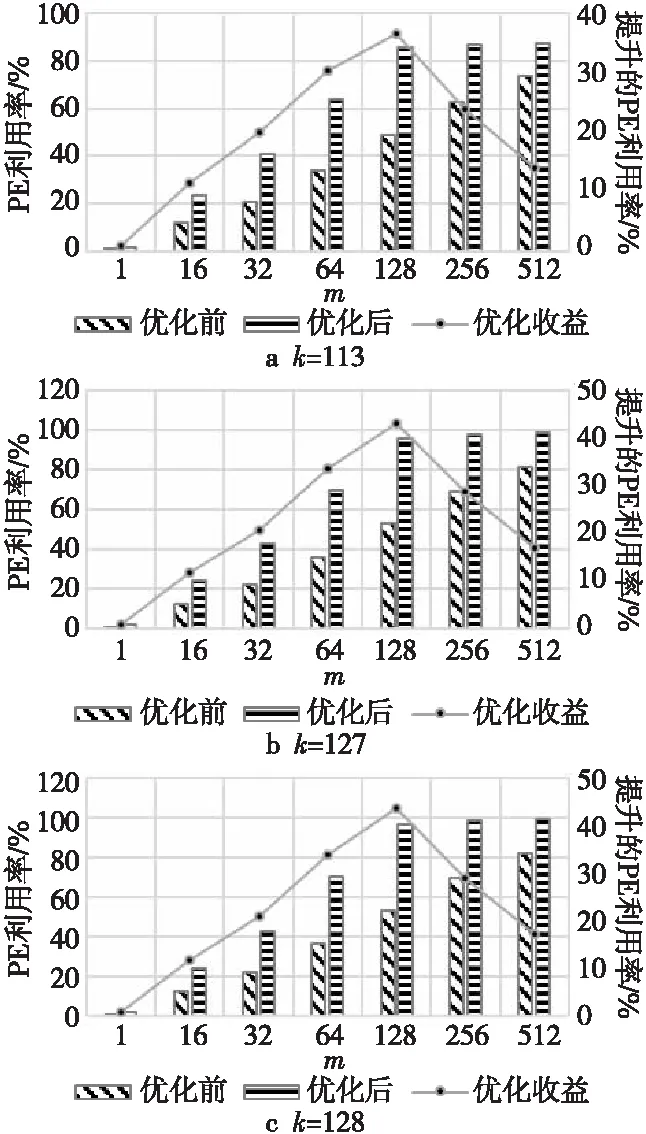
4.2 应用级工作负载及其性能分析

4.3 硬件开销对比

4.4 扩展性讨论
5 结束语

