基于可搜索加密的密态知识图谱存储和检索方案*
林 庆,滕 飞,田 波,赵 越,,祝锦烨,冯 力
(1.西南交通大学计算机与人工智能学院,四川 成都 611756;2.保密通信重点实验室,四川 成都 610041)
1 引言
知识图谱[1]是智能化数据应用的核心,其对抽取后的信息数据进行关联,将信息组织成一个庞大的知识库,从而赋能数据应用。近年来,知识图谱在医疗、金融及生活服务等多个领域得到了广泛的应用,在智能搜索、智能问答和大数据风控等应用中发挥出重要的作用。例如,利用知识图谱技术可以在金融领域实现反洗钱、识别高危用户及团伙等功能。这些知识图谱的构建建立在海量数据的基础之上,而这些数据中往往有着隐私敏感和多模态等特性。
知识图谱的存储与应用需要占用系统大量的存储和计算资源,将知识图谱数据外包到云服务器上,是一种节约资源成本且使资源高效利用的方式。由于云服务商不是完全可信的,其可以透明地窃取、篡改和泄露云服务器上的数据,造成数据机密性和完整性的破坏,所以将知识图谱存储到云服务器上有着隐私泄露等安全风险[2]。
防止数据泄漏的普遍共识是加密,直接对数据进行非确定性加密,如AES-CTR(Advanced Encryption Standard-CounTeR)[3],可以使数据具有很高的安全性,但是这将造成加密后的数据难以高效地进行操作(如检索)。因此,密码学研究人员开始研究如何在保证数据一定安全性的同时使数据可以高效地被使用,现在可搜索加密、同态加密和保序加密等方向有了很大的突破,其中可搜索加密可以使数据在密态条件下被检索[4]。2000年,Song等人[5]提出了第1个可搜索加密方案,该方案通过输入关键字可以在服务器上对密态文件进行检索;2012年,Kamara等人[6]首次提出了动态对称可搜索加密DSSE(Dynamic Symmetric Searchable Encryption)的概念;2014年,Cash等人[7]提出一种满足RCPA(Random-ciphertext- secure against Chosen-Plaintext Attack)安全的动态对称可搜索加密方案,该方案可高效地搜索百亿条记录关键字对,在方案设计上对本文有很大的参考意义。
现在已有较为成熟的关系型数据库加密方案如CryptDB[8]和Blind Seer[9]等,通过使用可搜索加密、同态加密等加密模型,可在密态条件下对关系型数据库进行有限的SQL操作。将知识图谱存储在关系型数据库上也是目前常用的一种方式[10],但是有许多关系型数据库加密方案不支持连接操作,而且密态条件下的连接操作是一个非常耗时的操作。由于知识图谱中有大量的多对多的关系,当使用关系型的数据模型来存储、管理知识图谱时,在查询、检索等操作上将需要大量的连接操作,所以使用关系型数据库加密方案并不适用于知识图谱的加密存储。
针对知识图谱在云服务器上存储所面临的问题,本文提出了一种基于可搜索加密的密态知识图谱EKG(Encrypted Knowledge Graph)存储方案,该方案支持知识图谱实体的一跳子图查询,主要工作如下所示:
(1) 提出了基于可搜索加密的密态知识图谱方案,该方案在不失去知识图谱的检索能力的前提下,为知识图谱提供机密性和完整性保护,通过使用密钥生成陷门的机制,也使得该方案有一定的身份认证能力。
(2) 考虑知识图谱中实体和其关系的关联性,对密态索引进行优化,在索引设计上加强了密态知识图谱在磁盘中存储的局部性,提高了检索效率。
(3) 提供了一种非密态知识图谱方案,该方案是一种知识图谱的非原生属性图存储方式,其图谱上的检索避免了关系型数据库上大量的连接操作,本文在其基础之上引入可搜索加密的设计思想,提出密态知识图谱方案。在真实数据集上对2个方案分别进行性能测试,并对密态方案进行安全分析,表明了所提出的加密方案在效率、有效性及安全性上取得了平衡。
2 预备知识
2.1 知识图谱数据模型
目前,主流的知识图谱数据模型有2种,分别为RDF(Resource Description Framework)图模型和属性图模型[10]。在知识图谱的存储管理中,RDF图模型和属性图模型最主要的区别在于属性的表达。在RDF图中,边可以作为属性谓词指向一个属性值,而所有的属性值都存储为节点,这给知识图谱上的图计算带来了更大的灵活性;在属性图中,属性结构是键-值对结构,这使得属性图在实现上更加简单。根据属性图的存储方式可以将属性图分为原生属性图和非原生属性图,原生属性图(如Neo4J)最大的特点是具有“无索引邻接(Index-free Adjacency)”特性,其底层存储设计是针对图数据库定制和优化的;而非原生属性图(如JanusGraph)使用通用的NoSQL数据库,比如HBase和键-值数据库(如RocksDB[11])等。由于属性图的简单特性,以及其与可搜索加密的适配度更高,本文方案中的知识图谱数据模型将采用属性图模型。
属性图由一组节点、边、属性和标签表示,数据节点和其边都用唯一ID命名,并且可以存储由键-值对表示的属性。属性图的形式化定义[10]如定义1所示:
定义1属性图G是五元组(V,E,ρ,λ,σ),其中,
(1)V是节点的有限集合;
(2)E是边的有限集合;
(3) 函数ρ:E→(V×V)将边关联到节点对,如ρ(e)=(v1,v2)表示e是从节点v1到节点v2的有向边;
(4)设Lab是标签集合,函数λ:(V∪E)→Lab为节点或边赋予标签,如v∈V(或e∈E)且λ(v)=l(或λ(e) =l),则l为节点v(或边e)的标签;
(5)设Prop是属性集合,Val是值集合,函数σ:(V∪E)×Prop→Val为节点或边关联属性,如v∈V(或e∈E),p∈Prop且σ(v,p)=val(或σ(e,p)=val),则节点v(或边e)上属性p的值为val。
如图1所示为病例图谱的属性图示例,其中每个节点和边都有唯一ID(如节点v2和边e3),节点和边都具有标签(如节点v2上的Guardianship和边e3上的suffer_from),节点和边上均可具有一组属性,每个属性由属性名和属性值组成(如节点v2上的属性name=“Bob”)。
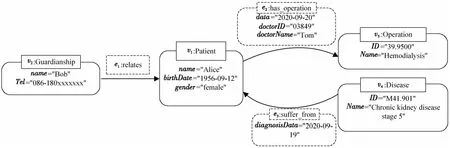
Figure 1 Property graph example:Case knowledge graph图1 属性图示例:病例知识图谱
2.2 可搜索加密
可搜索加密技术是搜索技术和加密技术的结合,其可分为对称可搜索加密SSE(Symmetric Searchable Encryption)和公钥可搜索加密PEKS(Public-key Encryption with Keyword Searching)[12]。SSE的构建方法一般分为基于存储结构和基于索引2种。基于存储结构的SSE方案的效率往往比较低,在搜索时需要服务器对整个加密数据集进行线性扫描并依次进行匹配;基于索引的构建方法的优势在于不需要特定的加密手段和存储结构,并且在搜索时有很高的效率。Curtmola等人[13]第一次正式定义了基于索引的SSE算法框架,具体如定义2所示:
定义2一个单用户的 SSE 方案的参与者包含1个用户和1个服务器,假设Δ是关键字字典,D⊆ 2Δ是文件集合,用户希望将文件集合D存储于服务器上,并且服务器可以提供对字典Δ的搜索服务,基于索引的对称可搜索加密算法SSE=(Gen,Enc,Trpdr,Search,Dec)的定义如下:
(1)K←Gen(1λ):由用户运行的一个密钥生成的概率性算法,以安全参数λ作为输入,输出密钥K。
(2) (I,c)←Enc(K,D):由用户运行的一个概率加密算法,以密钥K和文件集合D=(D1,…,Dn)作为输入,生成一个安全索引I和一系列密文集合c=(c1,…,cn)。
(3)t←Trpdr(K,w):由用户运行的一个确定性算法,输入密钥K和关键字w,输出一个用于检索的陷门t。
(4)X←Search(I,t):由服务器运行的一个确定性算法,通过索引I和陷门t来查找文件集D中是否含有关键字w的文件,并返回文件标识符的集合X。
(5)D←Dec(K,ci):由用户运行的一个确定性算法,根据X中标识符得到对应密文,用密钥K进行解密输出最终明文文件。
3 本文方案
本节将重点介绍密态知识图谱EKG方案的构建和检索过程。在介绍该方案之前将先介绍一种非密态知识图谱NEKG(Non-Encrypted Knowledge Graph)方案,主要阐述了将知识图谱数据编码为键-值存储模型的方式,以及在该方式下如何对知识图谱数据进行检索。该编码方式使得每个实体和其关系编码后的键-值数据有很好的局部性,在一跳子图查询时只需在磁盘中进行顺序读取。EKG方案在NEKG方案的基础上引入可搜索加密方案思想,该方案支持知识图谱数据的密态存储以及一跳子图查询。由于对编码后的键值数据经过加密后,数据原有的局部特性会丧失,所以在EKG方案中也考虑了实体和其关系的存储局部性。EKG方案引入了pos值,使其在检索过程中有更高的缓存命中率,从而减少IO次数。
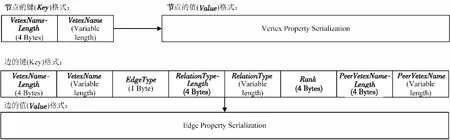
Figure 2 Key-value storage format for property graph图2 属性图的键-值存储格式
在这2个方案中所实现的检索方案为一跳子图查询,在知识图谱中,一跳子图查询是图谱查询的一个核心操作,通过一跳子图查询,可以在知识图谱上进行许多简单的推理[14]。一跳子图查询的定义如定义3所示:
定义3给定一个知识图谱KG和一个实体标识h,在KG中查询实体h以及实体h相关的所有关系Rh,在查询的过程中同时返回了实体和关系的属性,则称这个查询为一跳子图查询。
本节在方案描述过程中所使用的符号如表1所示。

Table 1 Description of main symbols
3.1 NEKG方案
在NEKG方案中,知识图谱通过属性图进行数据管理,该方式与关系型组织方式相比,避免了查询时要用到的大量连接操作。该方案将属性图的数据编码成键值数据并进行持久化存储,持久化后的键值数据存储于键-值数据库中的一个分区中。在属性图的存储中主要的数据是节点和边,其中节点可以用来表示知识图谱上的实体,边可以用来表示知识图谱上的关系。接下来将对NEKG方案中实体/节点和关系/边的键-值存储格式进行介绍。
如图2所示,在实体/节点键值存储格式中,VertexNameLength字段为实体名的长度,VertexName为一个独一无二的实体名称。在关系/边键值存储格式中,键的各个字段的含义如表2所示,EdgeType用来表示边的方向,大于0表示出边,小于0表示入边。关系/边在键值存储中的值(Value)为其属性的序列化。实体可以根据前缀VertexNameLength‖VertexName来匹配与其相关的关系。
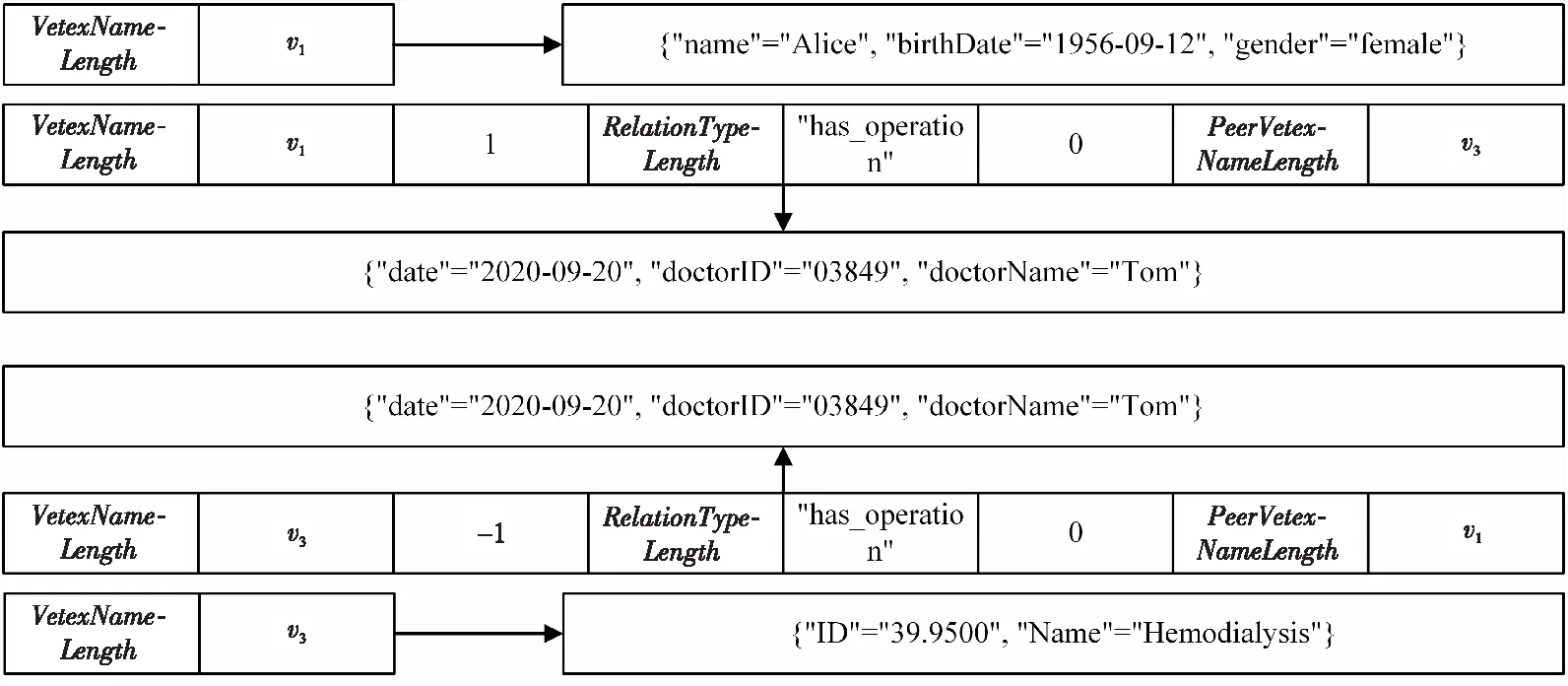
Figure 3 Example of encrypted key-value storage pattern 图3 键-值存储模式示例
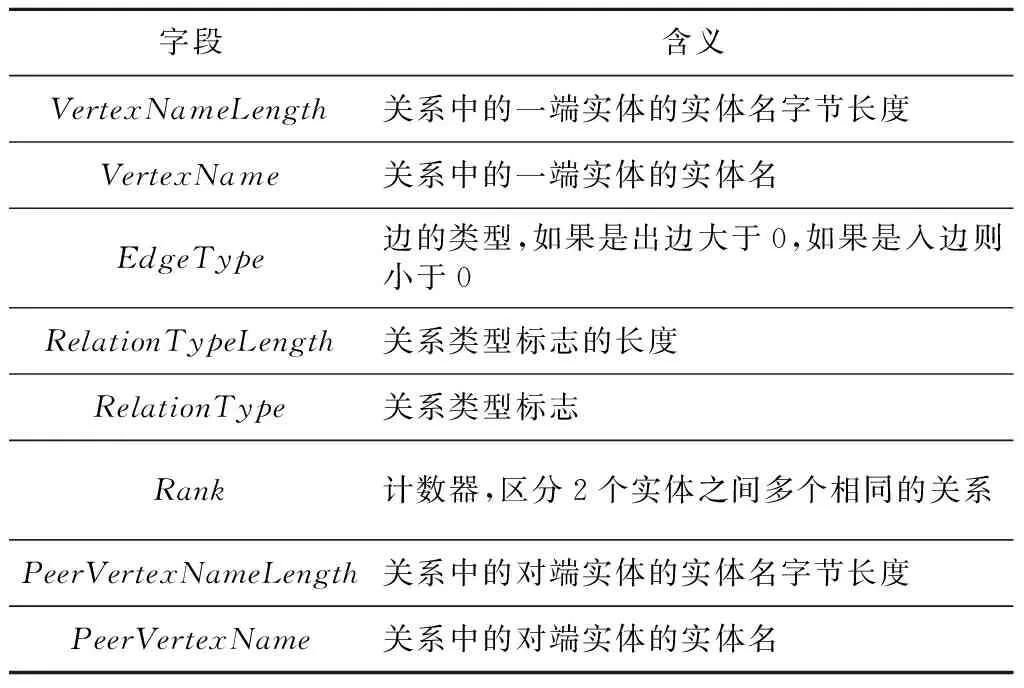
Table 2 Meaning of each field in edge key format
将图1中的节点v1、v3和边e2转化为键-值存储模式,转化后的格式如图 3所示。从图3中可以明显看到,在NEKG方案中,属性图中的每条边在键值存储中被建模为2个独立的键值对,分别表示出边和入边,而这样的设计可以通过前缀匹配,找出与节点相关联的所有边。
在NEKG方案中,构建和检索知识图谱非常简单。在构建中,只需要将实体和关系编码为键-值结构,然后直接存储到键值数据的一个分区中。在一跳子图的检索中,只需要将检索实体的标识(如实体名)编码为键-值结构中的键,之后通过键值数据库提供的前缀匹配功能,可以顺序读取到实体及其所对应的所有关系,由于都有相同的前缀,这个过程中所读取到的数据在磁盘存储中有很好的局部性。
3.2 EKG方案
可搜索加密方案通过对关键字建立密态索引,以支持对密态数据的检索。该思想在密态知识图谱的检索、存储设计中有重大的作用,可以将键-值数据库中的每个键作为关键字建立密态索引,以此来支持属性图模型下的密态操作。因此,在本文的EKG方案中使用基于键-值数据库的非原生属性图数据模型。
EKG方案主要实现了知识图谱数据在云服务器中的加密存储,同时可以支持用户对该加密的知识图谱进行一跳子图的查询。如图4所示,EKG方案中的系统结构可分为可信区域和不可信区域,其中,可信区域为用户和数据拥有者内部的代理服务器,不可信区域为云服务器。在构建过程中,代理服务器将加密后的密态数据和陷门交给云服务器,云服务器对密态数据进行进一步处理后在键-值数据库中进行持久化。在检索过程中,用户向代理服务器发起查询请求,代理服务器通过用户的查询请求,产生查询陷门,在云服务器上进行密态检索,云服务器将密态检索到的密文数据返回给代理服务器,代理服务器将密态数据解密后发送给用户。本节将对EKG方案的构建和检索过程进行详细介绍。
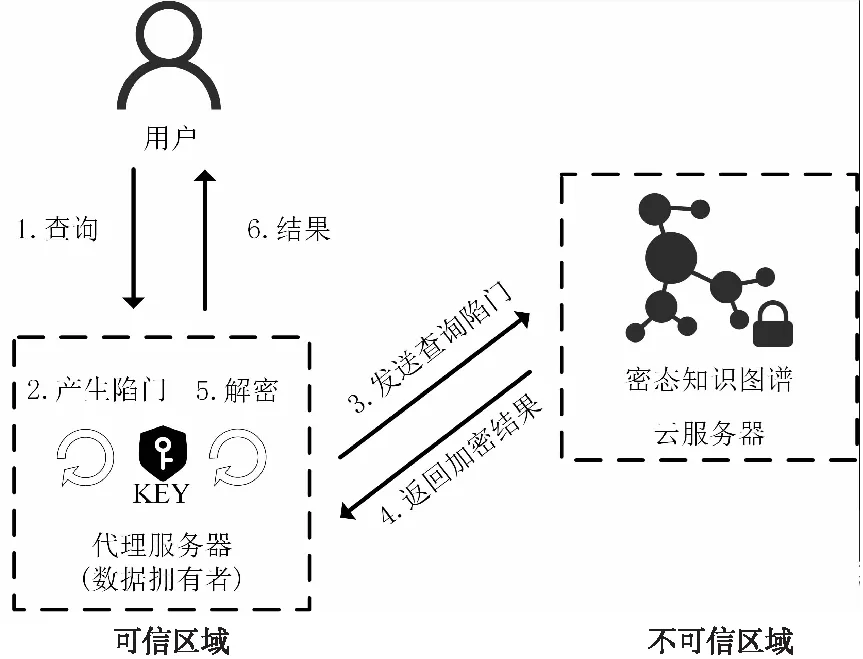
Figure 4 Diagram of system structure图4 系统结构图
3.2.1 构建方法
在构建过程中,代理服务器需要将陷门传递给云服务器,云服务器通过陷门再进行进一步的加密处理,从而构建密态索引。陷门的生成算法如算法1所示。
算法1陷门生成算法(GenTd)
输入:实体或关系编码为键-值模式后的键key;代理服务器上的密钥k。
输出:一对陷门〈tdx,tdy〉。
1.tdx←MAC(k,1‖key);
2.tdy←MAC(k,2‖key);
3.RETURNtdx,tdy
如图5所示,EKG方案的知识图谱构建主要分为以下4个步骤:
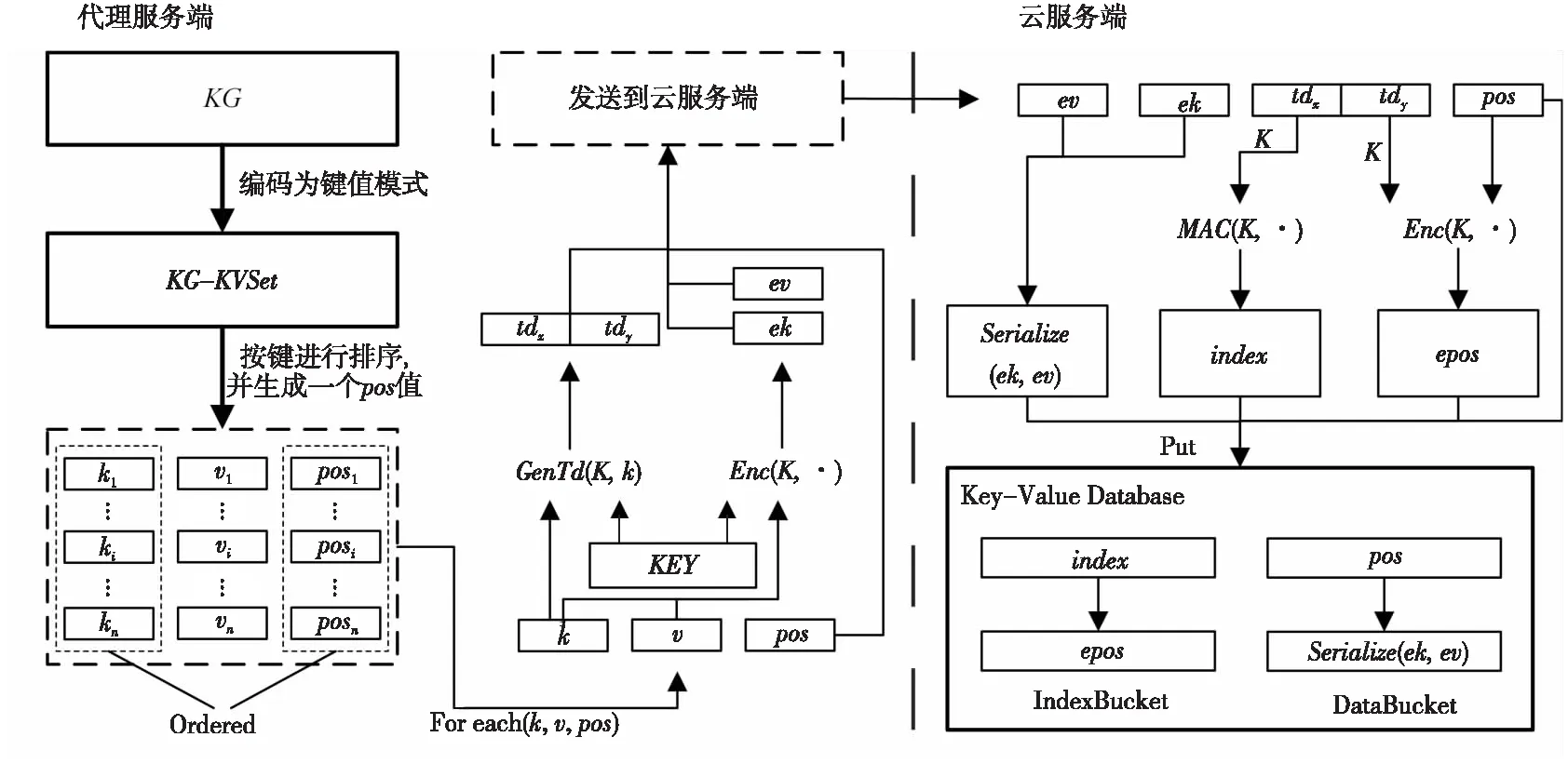
Figure 5 Knowledge graph construction process图5 密态知识图谱构建过程
(1)将知识图谱中的实体和关系编码为键值结构,该步骤与NEKG方案中的编码方案一致。
(2)对编码后的键值数据按键进行排序,并为其产生一个有序的pos值,生成〈ki,vi,posi〉(1≤i≤|E|+|R|×2)元组集合。
(3)对每个〈ki,vi,posi〉中的ki产生一对陷门,并对ki,vi进行加密,生成〈tdxi,tdyi,eki,evi,posi〉元组,并将该元组发送到云服务器中。
(4)云服务器对(eki,evi)进行序列化后,将{posi,Serialize(eki,evi)}存入DataBucket中,持久化密态知识图谱数据。将{MAC(tdxi,1),Enc(tdyi,posi)}存储到IndexBucket中,构建密态索引。
在EKG方案中,加密索引存储于键-值数据库的IndexBucket分区中,加密数据存储于键-值数据库的DataBucket分区中。通过在索引IndexBucket中找到epos,并将该值解密,便可在DataBucket中找到所对应的数据。由于密态知识图谱中有大量的实体和关系,采用内存数据库(如Redis)来存储构建后的密态知识图谱不太现实,所以在设计EKG方案时所考虑的场景是基于磁盘键值数据库存储的,而不是基于内存的。磁盘键值数据库大多数都是基于LSM-Tree(Log Structured Merge Tree)[15]实现的,因此使用有序的pos值可以使实体及其关系在磁盘中存储在同一个或相邻的SSTable段,这样的设计可以让检索过程具有更高的缓存命中率,避免了过多的磁盘IO次数,从而提高了检索效率。
3.2.2 检索方法
在键-值模式中,一跳子图查询需要通过实体标识(键)检索到实体所对应的属性(值),同时检索该实体相关的关系(键)及关系的属性(值)。
如算法2所示,在代理服务端中,一跳子图查询依赖于SecGet和SecNext算法。如算法3所示,SecGet算法用于查询实体的属性值,在查询的过程中,通过将实体在键-值存储模式中的键所产生的陷门发送到云服务器上,云服务器利用陷门在密态索引IndexBucket中得到epos值,通过epos解密得到的pos值检索到存储在DataBucket中的对应的密态数据,并将检索到的密态数据返回给代理服务端。SecNext算法用于检索实体对应的关系和关系属性,其实现借助本方案所设计的pos值,pos值是按明文状态下键的字典序所获得的一个有序值,由于实体和其对应的关系编码为键-值模式后,其键在字典序上是连续的,这意味着对应的加密数据在Databucket中也是连续存储的,所以通过该算法可以获得实体相关的边及其属性。因此,将这2个算法调用所获得的明文数据组织起来,将是一个一跳子图查询的结果。在云服务器的整个查询过程中,所查询的数据始终是加密状态的。这2个算法都需要向云服务端传递陷门。该陷门有2个作用,第1个作用是用于在密态索引中检索到密态知识图谱数据,第2个作用是用于身份认证,只有代理服务端拥有生成陷门的密钥。因此,其他没有密钥的攻击者想伪造陷门进行检索是不可行的,能够成功检索到数据的就只能是安全区域中的代理服务器。
算法2一跳子图查询
输入:在键-值存储模式下实体所对应的键w;代理服务器上的密钥k。
输出:所检索实体的一跳子图SubG。
1.h←SecGet(w);
2.it←w;
3.w*,r*←SecNext(it);
4.WHILEw*≠ ⊥do
5.Add(w*,r*) toRh;
6.it←w*;
7.w*,r*←SecNext(it);
8.ENDWHILE
9.SubG←Build(w,h,Rh);
10.RETURNSubG
算法3实体查询算法(SecGet)
输入:在键-值存储模式下实体所对应的键w;代理服务器上的密钥k。
输出:在键-值存储模式下键w所对应的值ew′,即实体的属性。
1.//run in proxy server
2.tdx,tdy←GenTd(w,k);
3.ed←CloudGet(tdx,tdy)/*remote procedure call,send a pair of trapdoor to cloud server,receive the encrypted data*/
4.ek,ev←Deserialization(ed);
5.w′←Dec(k,ek);
6.ew′← ⊥;
7.IFw′=wTHEN
8.ew′←Dec(ev,k);
9.ENDIF
10.RETURNew′
11.//run in cloud server
12.CloudGet(tdx,tdy)
13.idx←MAC(tdx,1);
14.epos←Get(IndexBucket,idx);
15.pos←Dec(tdy,epos);
16.ed←Get(DataBucket,pos);
17.RETURNed
SecNext算法(如算法4所示)中体现了pos值的设计给方案带来的好处,每次调用SecNext所检索的数据在磁盘中的存放位置总与上一次迭代检索的数据相邻,不仅大幅度减少了磁盘随机读的次数,而且也使得一跳子图查询过程有更高的缓存命中率。
算法4关系查询算法(SecNext)
输入:在键-值存储模式下实体或关系所对应的键w;代理服务器上的密钥k。
输出:在键-值存储模式下与w有相同前缀的关系对应的键值对〈w′,rw′〉。
1.//run in proxy server
2.tdx,tdy←GenTd(w,k);
3.ed←CloudNext();//remote procedure call
4.ek,ev←Deserialization(ed);
5.w′←Dec(k,ek);
6.rw′← ⊥;
7.IFmatchPrefix(w′,w) is trueTHEN
8.rw′←Dec(ev,k);
9.RETURNw′,rw′;
10.ELSE
11.RETURN⊥;
12.ENDIF
13. //run in cloud server
14.CloudNext(tdx,tdy)
15.idx←MAC(tdx,1);
16.epos←Get(IndexBucket,idx);
17.pos←Dec(tdy,epos);
18.ed←Next(DataBucket,pos);
19.RETURNed
4 安全分析
4.1 存储安全性分析
在EKG方案中,加密索引和加密数据分别存储在IndexBucket和DataBucket 2个分区中。在IndexBucket中,{index,epos}分别为ek的消息认证码MAC(Message Authentication Code)和pos经过非确定性加密后形成的密文。在DataBucket中,{pos,Serialize(ek,ev)}分别为有序标识pos值和键值数据经过非确定性加密后所序列化成的二进制串。EKG方案在整个存储过程中需要使用MAC生成算法和非确定性加密算法。
对于涉及的MAC生成算法,本文方案均采用HMAC-SHA256,HMAC的安全性取决于底层哈希函数的安全性。SHA256是一种安全的哈希算法,目前仍未找到有效的攻击算法能在多项式时间内找出SHA256的一对碰撞,所以本文所采用的HMAC-SHA256是安全的,其可以抵抗选择信息攻击,攻击者并不能在多项式有效的时间内找到存在性伪造。
涉及的对称加密算法的设计均采用AES-CTR模式,其满足选择明文攻击下的不可区分性安全IND-CPA(INDistinguishability under Chosen-Plaintext Attack)[16],对比更普遍常用的AES-CBC(Advanced Encryption Standard-Cipher Block Chaining)模式[17],有着可并行、不需要填充以及安全性更高等优势。在同样选用AES-128的情况下,CTR模式在加密264个AES 块后必须更换密钥,而CBC模式则在加密248个AES块后必须更换密钥,相比之下CTR模式的安全性更加优越。CTR模式中对每个分组是可以独立运算的,这也意味着该模式可以通过并行计算来提高系统效率,这一点对于链式结构的CBC模式来说是做不到的。
在整个构建和存储过程中,为了获得更快的检索效率,密态知识图谱会向服务器泄露有序的pos值,但是所泄露的pos值不会向攻击者泄露任何明文信息。综上所述,当本文所设计的密态知识图谱暴露在恶意环境下时,攻击者所能够获取到的只有隐私数据的索引对数,以及有序的pos值。由于知识图谱数据经过满足IND-CPA安全性的非确定性加密算法加密,因此攻击者不会获得有关知识图谱的任意实体/关系的明文信息。
4.2 检索安全性分析
在密态知识图谱的检索过程中,代理服务端通过基于密钥的消息认证码算法HMAC,利用知识图谱键-值存储模式下的键构造一对陷门〈tdx,tdy〉,并将陷门对发送到云服务端。由于本文方案HMAC算法所依赖的散列函数有着可靠的抗碰撞性及不可逆性,所以构造出来的陷门并不会泄露任何明文信息。云服务器收到陷门对后,系统将利用tdx来生成一个MAC值,通过该MAC值在索引分区IndexBucket中找到epos值,再通过tdy将epos解密得到pos值,通过pos值在DataBucket分区中找到对应的加密知识图谱数据返回给代理服务器。在这个过程中,涉及到的被检索数据对敌手来说都是密态的,对应的每个实体和关系的存储都是被满足IND-CPA安全的对称加密算法所加密保护的,因此敌手无法在此过程中获取到用户隐私数据。本文方案的安全索引是基于Cash等人[7]的动态可搜索加密方案所构建的,其整个构建被严格证明为符合Cash等人所提出的RCPA(pseudo Random Ciphertexts under chosen-Plaintext Attack)安全性。
5 实验及其结果
本文在Freebase Film Data数据集上对NEKG方案和EKG方案进行了全面的实验分析。NEKG和EKG方案通过Golang实现,键-值数据库使用Badger DB v3.2。代理服务端和云服务端实验运行环境均为Ubuntu20.04 LTS,处理器的核心数为4,内存容量为4 GB。其中EKG方案系统原型部署在代理服务端和云服务端,而NEKG方案的系统原型部署在云服务端,为了避免网络环境不稳定对实验数据的影响,代理服务端和云服务端均为本机上的2台虚拟机。
为了测试随着数据规模的增加EKG方案和NEKG方案的构建时间和空间的变化情形,以及对比和分析不同数据规模下2个方案在构建时间和空间上的差异,本文分别在不同数据规模下对这2个方案进行性能测试。构建知识图谱的测试规模如表 3所示,其中最大规模的实体数量达到了百万级别。构建时间的实验结果如图 6所示,其中,y轴表示构建时间,x轴表示实体和关系数量的总和。从实验结果可以看出,构建时间与实体和关系数量的总和呈线性关系,并且EKG和NEKG之间的构建时间差异并没有高于一个数量级。
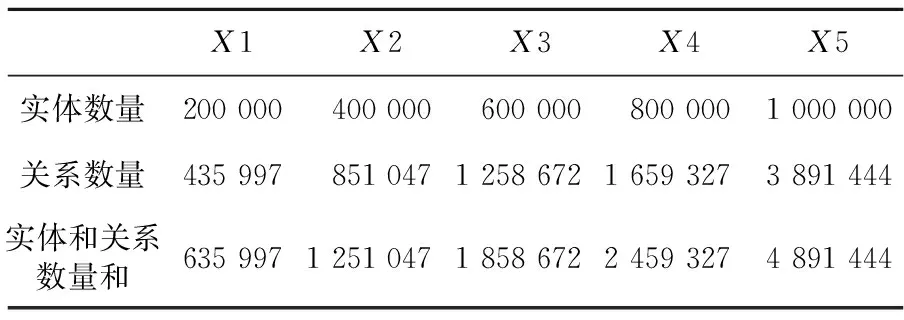
Table 3 Test scales of knowledge graph construction
构建后的知识图谱所占空间如图 7所示,其中,y轴表示图谱所占空间,x轴表示实体和关系数量的总和。从实验结果可以看出,知识图谱的存储空间与实体和关系数量的总和呈线性关系,EKG方案中知识图谱所占空间大小约为NEKG方案的3倍,而这相对于现今的磁盘存储成本是可接受的。下面分析空间膨胀的原因:在EKG方案中,每个实体或关系所编码成的键-值将被加密,加密的填充机制会导致加密后的数据在字节数上膨胀;另一方面,对于每对明文键-值,其密态存储时需要分别在IndexBucket和DataBucket中存储密态索引和密态数据。
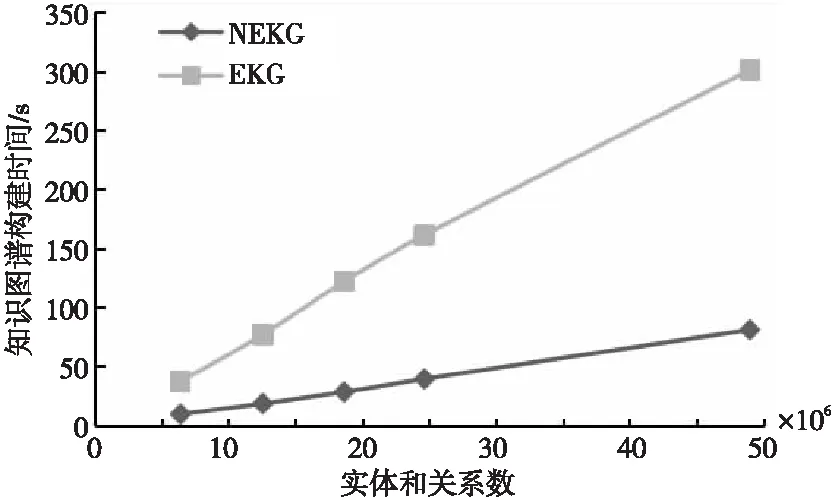
Figure 6 Test results of knowledge graph construction time 图6 知识图谱构建时间测试结果
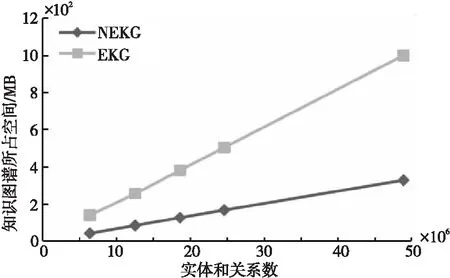
Figure 7 Test results of knowledge graph storage space 图7 知识图谱存储空间测试结果
为了测试EKG方案和NEKG方案的一跳子图平均检索效率以及对比这2个方案的差异,本文在所构建的1 000 000实体规模的知识图谱上进行查询测试,从中随机抽取出100 000个实体标识作为查询集,分别对NEKG和EKG方案进行20 000,40 000,60 000,80 000和100 000次一跳子图查询。查询时间的测试结果如图 8所示,其中,y轴为一跳子图查询时间,x轴为从查询集中顺序读取实体标识进行检索的个数。从实验结果可以看到,在100 000次检索测试中,EKG的检索时间为NEKG的2.09倍,EKG方案中对于每一个实体或关系,其在云服务器中需要2次读数据库操作,而NEKG方案只需要1次读数据库操作,并且在EKG方案中,在代理服务端中需要生成查询陷门,并且对从云服务器中获取到的密文进行解密,在云服务端也需要额外的加解密计算,可见2.09倍是一个可观的实验结果。
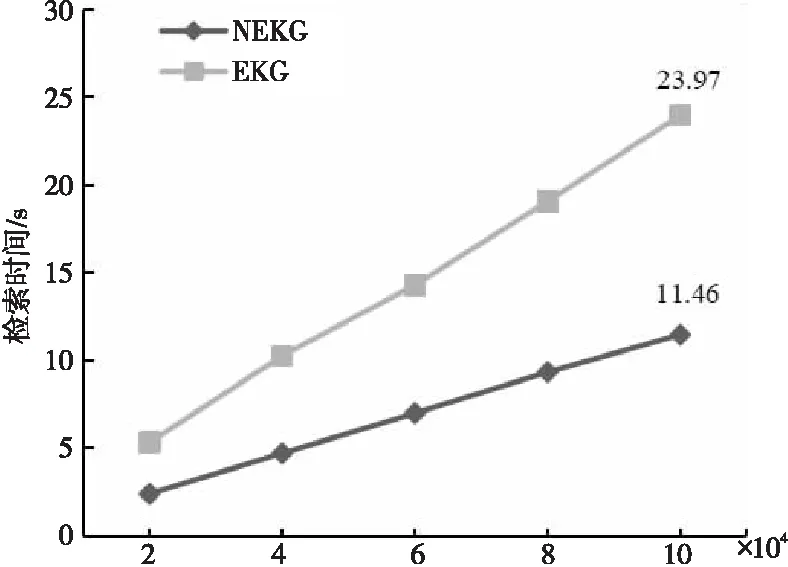
Figure 8 Test results of one-hop subgraph query time 图8 一跳子图查询时间测试结果
为了更好地了解NEKG和EKG方案在查询的各个步骤的耗时,本文将查询划分为4个子步骤,如表 4所示。通过前文的方案介绍可知,对于NEKG方案,一跳子图查询主要为2个步骤,分别为从键值数据库中读取键值数据(T2-NEKG),以及键值模型和图模型之间的转换(T4)。对于EKG方案,一跳子图查询主要有4个步骤,在查询实体/关系所对应的键值之前,需要先生成陷门(T1),将生成后的陷门发送到云服务器中,云服务端将检索到的加密数据返回给代理服务器(T2-NEKG),将加密数据解密为明文的键-值数据(T3),最后再将键值模型数据转化为图模型数据(T4)。本文在100 000次一跳子图查询下对各个子步骤的总耗时进行测试,测试结果如图 9所示。EKG方案和NEKG方案查询过程最大的区别在于T2-EKG和T2-NEKG,其中T2-EKG为T2-NEKG的2.54倍,原因在于EKG每查询一个明文键值需要读取2次键值数据库,并且云服务端在读取完数据之后,需要执行Hash算法和解密算法。

Table 4 Query substep of one-hop subgraph
目前所有实验都是基于多次查询时间的总和所得出的结论,而对于某些热点实体,其可能拥有很多关系也有可能拥有很多属性,这些实体往往在查询时需要更多时间,而对于这些实体恰好是最有可能被用户所检索的实体。所以,本文对100 000次查询测试结果中的百分位数进行了统计,如图 10所示,在P999百分位点中,EKG方案的查询时间为NEKG方案的2.26倍。从实验结果可以得出,热点实体对于EKG方案和NEKG方案之间的查询速度比影响很小,这充分表明EKG方案在安全性和效率上取得了很好的平衡。
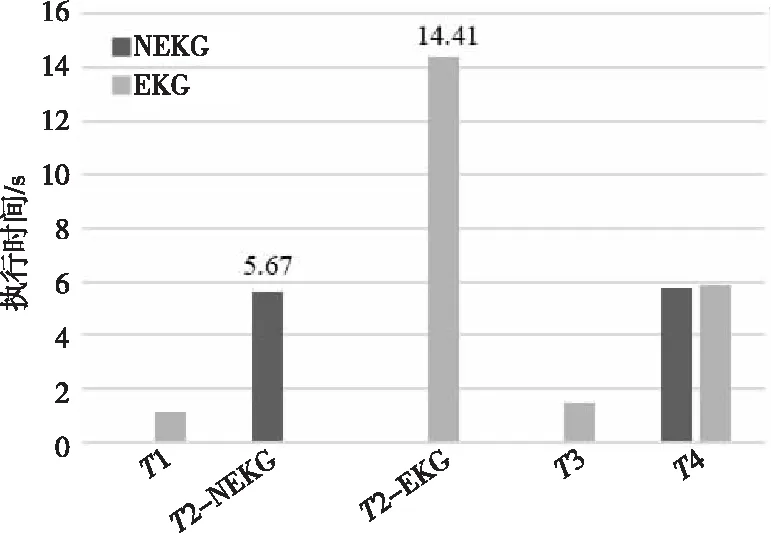
Figure 9 Substep time-consuming of one-hop subgraph query 图9 一跳子图查询子步骤耗时情况

Figure 10 Percentile points among 100 000 queries图10 100 000次查询中的百分位点
6 结束语
本文提出了一种基于可搜索加密的密态知识图谱方案,该方案支持知识图谱的密态存储以及一跳子图查询。为了获得更好的检索性能,该方案引入了一个有序的pos值,使实体及其所对应的关系能在磁盘中局部存储,增加缓存的命中率,减少IO次数。经过与非密态的知识图谱之间的性能对比,证实了该方案在安全性和效率上取得了良好的平衡。后续将在此研究的基础之上,对存储和加密计算进行并行优化,并引入同态加密和保序加密等功能性加密方案,使密态知识图谱方案实现更多的密态知识计算。目前该方案仅支持全密态化的知识图谱存储,而对于知识图谱中的非隐私数据往往可以不需要密态化存储,因此,未来如何设计并实现仅针对隐私数据加密的半密态知识图谱将是研究的一大关键。

