大高差区域最优GNSS高程异常拟合模型的确定

李圣明，史俊波，李 林，董新莹

（1.中交第二公路勘察设计研究院有限公司，湖北 武汉 430050；2.武汉大学 测绘学院，湖北 武汉 430079）

经典GNSS高程拟合基于“移去—拟合—恢复”的思想[1]，引入EGM2008地球重力场模型和DEM格网数据，分别确定长波项和短波项，最后选择合适的拟合模型计算高程异常残余项。多项式拟合法是最常用的高程拟合模型之一，构建多项式拟合模型后，利用已知点真值，基于最小二乘准则确定未知参数，外推得到未知点的高程异常大小。唐诗华[2]等系统地研究了不同估计方法的原理和特点，得出最小二乘估计在高程拟合中精度最高的结论；陈安平[3]等比较分析了二次曲线拟合法和三次曲线拟合法等模型的适用性和可靠性；王雪林[4]和杨坤[5]等通过实际测量数据证明了多项式曲线拟合法可满足四等水准测量要求，但涉及的测区均处于地势平坦的区域，相对高差较小。多项式拟合法模型简单、应用广泛，但不适用于起伏较大的测区。因此，针对大高差区域，本文利用反距离加权法和支持向量机（SVM）模型进行高程异常残余项的拟合；再通过实际算例，比较分析了不同模型的拟合效果，给出大高差区域最优GNSS高程异常拟合模型的建议。

1 研究原理与方法

1.1 多项式拟合模型

多项式拟合模型是将呈带状分布的联测点视为一个曲面，认为曲面上各控制点的高程异常与其坐标xi（或yi）之间存在函数关系。本文以xi为自变量，高程异常模型可表示为：

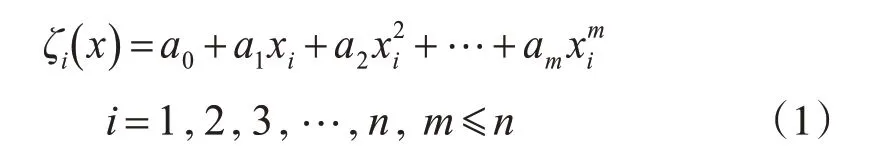
式中，a0,a1,…,a m为待定系数。

对于每个(xi,yi,ζi)，联立上述方程进行拟合后，再利用最小二乘法求解式（1）中的各项系数并代回，即可求出曲面上任意一点的高程异常值。

1.2 反距离加权模型

反距离加权法[6]常见于散点数据的插值应用中，适用于散点分布较均匀的情况。待求点P处的高程异常插值结果ζP，即为测区内所有已知点高程异常值ζi(i=1,2,…,n)的加权和。

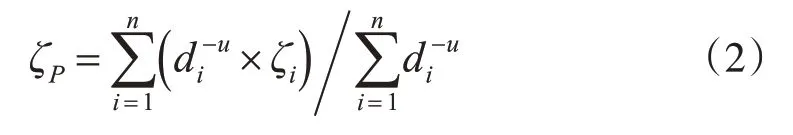
式中，di为第i个已知点到待求点P距离；u决定距离增加时权重减小程度。

1.3 SVM模型

SVM[7]模型，即某区域的N个训练样本点可表示为{(xk,y k)|k=1,2,…,N}，其中xk∈Rn为n维两列输入向量，两列分别为坐标x和y；y k∈R为n维1列输出向量，代表已知点的高程异常残余项。利用非线性映射φ(x k):Rn→Rnk将输入空间的非线性回归问题转换为高维特征空间中的线性回归问题，可表示为求解以下约束优化问题：

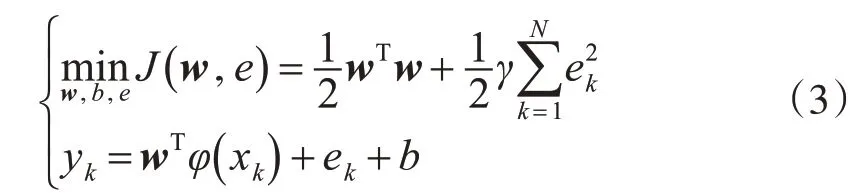
式中，w∈Rnk为权向量；γ为调整参数；b为偏差量；e k∈R为误差变量。

2 研究结果与分析

本文选取两个算例验证上述高程异常拟合模型。算例1：数据点分布在东西5.35 km、南北15.19 km的范围内，最高最低海拔差距约为445.9 m，将其中9个联测点作为已知点，28个联测点作为检核点。算例2：数据点分布在东西20.22 km、南北12.95 km的范围内，最高最低海拔差距约为705.4 m，将其中9个联测点作为已知点，38个联测点作为检核点。算例点位分布情况如图1所示。

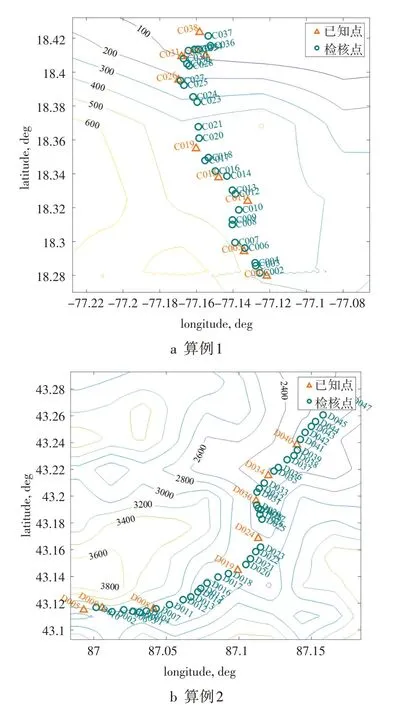
图1 算例1和算例2的点位分布

根据参与建模的已知点的高程异常真值ζi和计算得到的高程异常值ζiY，求得残差Vi Y=ζi-ζiY，作为内符合精度。根据参与检核的各点高程异常真值ζi和计算得到的高程异常值ζiC，求得残差Vi C=ζi-ζiC，作为外符合精度。利用多项式拟合法对算例1和算例2的9个已知点进行高程异常残余项建模，并统计内符合残差，如图2、3所示。

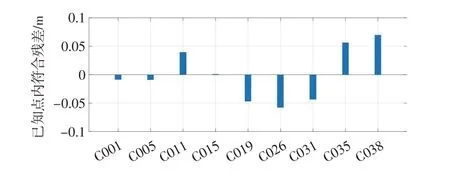
图2 算例1多项式拟合法建模内符合残差

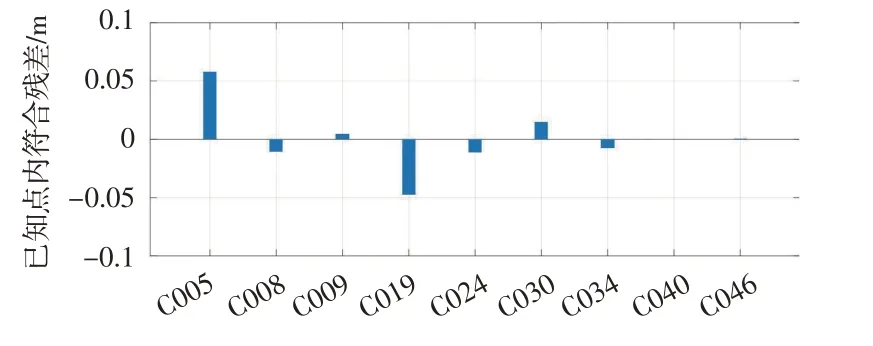
图3 算例2多项式拟合法建模内符合残差

利用多项式拟合法、反距离加权法和SVM模型对算例1的28个检核点和算例2的38个检核点进行检验计算，外符合残差对比如图4、5所示。

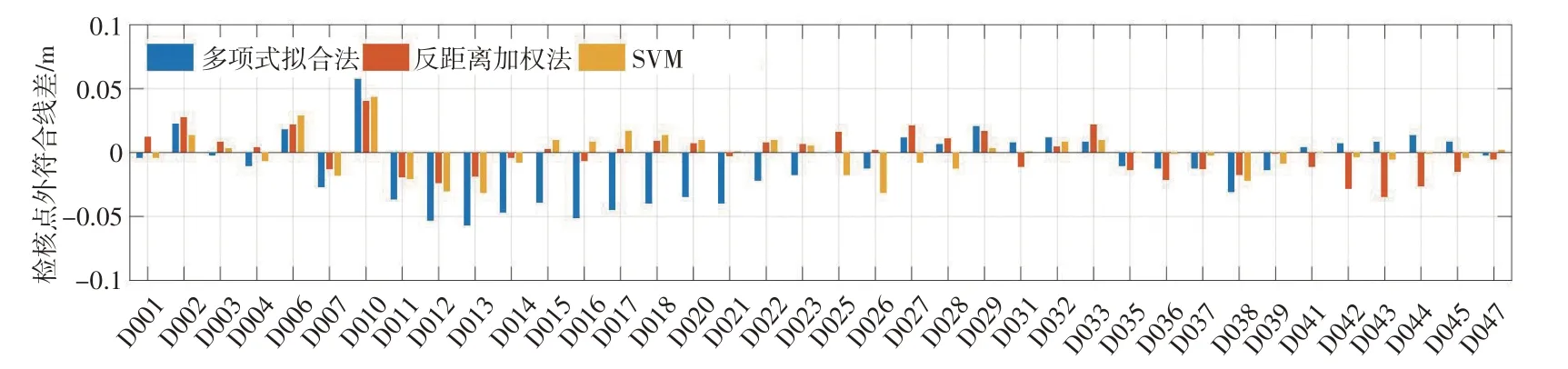
图5 3种模型外符合残差对比（算例2）

两个算例的区域特征以及检核点采用3种模型计算得到的外符合残差平均值如表1所示，绘出的对比图如图6所示，可以看出，多项式拟合法总体上能达到高程拟合的精度要求，但精度略差于另外两种模型；反距离加权法和SVM模型体现出良好的适用性，外符合残差的差距分别为0.52 cm和0.27 cm；综合两个算例结果判断，在地势起伏比较大的崎岖地区，SVM模型精度优于反距离加权法。

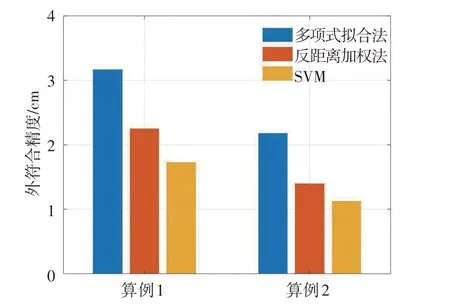
图6 3种模型精度对比图

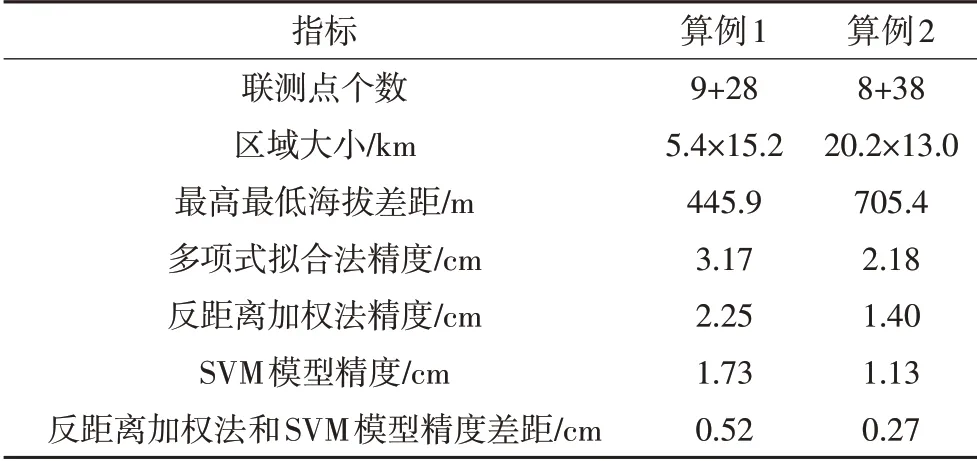
表1 高程拟合算例综合分析

3 结语

针对高程转换时常用的多项式拟合法在大高差区域适用性较差的问题，本文将反距离加权法和SVM模型替代了多项式拟合法；并通过两个最大高差分别为445.9 m和705.4 m的实际算例比较分析了3种模型在大高差区域对于高程异常残差项的拟合效果。结果表明，利用SVM模型的外符合精度分别为1.73 cm和1.13 cm，优于反距离加权法的2.25 cm和1.40 cm和多项式拟合法的3.17 cm和2.18 cm。因此，SVM模型可作为大高差区域GNSS高程异常拟合模型的最优选择。