橡胶复合材料中炭黑微观结构图像的拟合算法

何 红，陈增云，张亚茹，章易慎，张立群，李凡珠*

（1.北京化工大学 有机无机复合材料国家重点实验室，北京 100029；2.北京化工大学 机电工程学院，北京 100029）

作为理想填料，炭黑可以提升橡胶材料的力学性能，广泛应用于轮胎和橡胶制品中[1-2]。炭黑补强橡胶复合材料的微观结构是决定其物理和化学性能的主要因素，研究其微观结构[3]是调控和设计炭黑补强橡胶复合材料性能的重要途径。目前，常用电镜图像分析法[4]，即用扫描电子显微镜获得复合材料截面图像，以分析其微观结构。但在炭黑补强橡胶复合材料的建模和性能仿真中，由于复合材料微观结构图像中炭黑粒子的堆叠存在显示缺陷，无法采用真实结构参数进行计算，导致仿真结果无法预测复合材料的真实性能。因此，开展炭黑补强橡胶复合材料微观结构重构的研究具有十分重要的意义和价值。

炭黑补强橡胶复合材料微观结构重构和性能预测研究现在仍处于初级阶段。国外已开发了OOF2软件[5]图像处理技术和透射薄片3D-TEM[6-8]技术。OOF2软件图像处理技术可以将复合材料二维电镜图像直接导入软件建模，并在软件中对模型直接进行后处理和模拟计算，但是该软件在图像前处理方面存在不足，其图像处理模块及方法简单，无法适用于复杂结构的图片，而且处理精度不足。3D-TEM技术则是通过扫描复合材料薄片得到其三维微观结构并进行仿真，复合材料微观结构三维模型虽与实际微观结构相近，但是由于设备和测试费用昂贵，该技术难以普及。国内基于这2种技术开展了相关的图像与建模研究[9-11]，但对于微观结构图像的建模研究还鲜见报道。

针对上述问题，本工作基于炭黑补强橡胶复合材料微观结构图像，采用3种拟合算法重构炭黑聚集体微观结构，通过拟合算法的精度研究，探索炭黑聚集体结构重构的最佳方法，从而为炭黑补强复合材料性能的预测奠定基础。

1 炭黑补强橡胶复合材料微观结构图像的形态拟合

1.1 炭黑形态

将烃类物质在工业反应炉内进行不完全燃烧，在极短时间内生成炭黑原生粒子，继而再生长形成聚集体，最终成为粉末状炭黑[12]。根据长宽比，炭黑聚集体形态可分为球形、椭圆形、线形和分支类[13-14]。其中分支类聚集体形态最为复杂，可视为其他3种形态的聚合。从炭黑的生成可以得出，炭黑呈聚集体形态，而聚集体由原生粒子构成，为此本工作按照将炭黑原生粒子视为圆形粒子、炭黑聚集体则由多个圆形原生粒子构成的思路进行炭黑微观结构图像的拟合。

1.2 图像背景处理

由于炭黑补强橡胶复合材料微观结构电镜图像存在光照不均匀、炭黑与橡胶基体界限不明显等缺陷，需要对其进行背景处理，处理过程如下。

首先，采用图像分割、滤光算法和高斯滤波器处理电镜图像，以达到光照均匀的效果。图像分割可减少整体光照信息，滤光算法[15]可提取图像中的亮度信息，高斯滤波器可去除光照误差。具体做法为：在识别整张电镜图像尺寸信息后，根据设置的横向与纵向间隔数将图像等分，再将每一部分进行滤光处理，提取光线信息后通过伽马函数与图像像素进行卷积以实现亮度平均，最后再将分割的各部分图像进行合并。

其次，采用阈值迭代方法处理图像中炭黑与橡胶基体界限不明显的问题。由于研究对象为炭黑与橡胶两部分，使用一个初始阈值将图像分为两部分，再令两部分的分界不断逼近真实阈值。求取最佳阈值的流程（见图1）如下：首先定义灰度图的灰度平均值为初始阈值（Zt），通过遍历整个图像像素F（x，y），将每一点的像素与Zt进行比较，大于Zt部分分配给S1（大于Zt的各点像素和），小于Zt部分分配给S0（小于Zt的各点像素和），将S1与S0各自求取平均值，得到灰度值大于Zt的平均值（Zj）与灰度值小于Zt的平均值（Zi），再将Zj与Zi取平均值（Zt1）；比较Zt1与Zt，若二者差值大于0.1，则将Zt1作为新的Zt重新循环计算，直到2次循环的Zt1与Zt差值小于0.1为止；最后的阈值定义为最佳阈值。

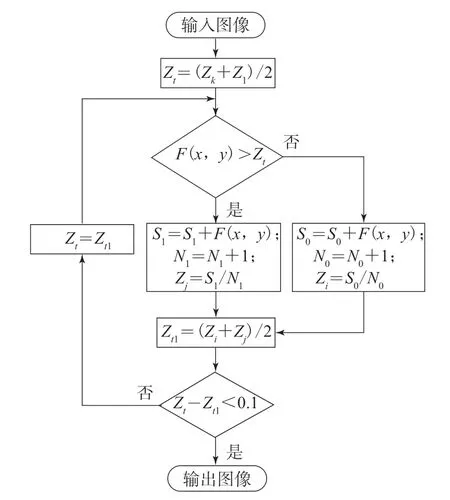
图1 阈值迭代算法流程Fig.1 Flowchart of threshold iteration algorithm

1.3 拟合算法及微观图像的拟合

在炭黑补强橡胶复合材料微观结构的电镜图像中，炭黑聚集体形态多样。根据前述思路，将炭黑原生粒子看作圆形，通过圆心位置的排布来重构原生粒子聚集体形态模型。图像数字化信息包含位置信息与灰度信息。拟合算法有3种：根据图像中炭黑聚集体轮廓位置信息拟合炭黑形态，分为炭黑原生粒子为等径圆拟合的轮廓骨架算法（第1种拟合算法）和非等径圆拟合的最大内切圆算法（第2种拟合算法）；根据灰度信息进行拟合，可采用炭黑原生粒子为非等径圆的K-means聚类算法（第3种拟合算法）。

拟合算法中使用的炭黑原生粒子直径为复合材料电镜图像中原生粒子实际测量直径。采用Nano Measure软件标记复合材料电镜图像炭黑原生粒子直径，测量数据多于50组，根据比例关系换算得到炭黑聚集体粒径及其分布。使用测量的炭黑原生粒子直径的平均值作为等径圆拟合算法中的拟合圆直径，使用测量的炭黑原生粒子直径的范围[（Lmin，Lmax），Lmin和Lmax分别为电镜图像中炭黑原生粒子直径的最小值和最大值]作为非等径圆拟合算法中拟合圆直径的范围。

轮廓骨架算法拟合炭黑聚集体形态过程如下。首先采用Canny算子识别炭黑聚集体形态轮廓，然后使用bwmorph函数对图像进行骨架化，目的是通过对图像进行形态学腐蚀，得到依然保持原本形状的细化像素，最终保留宽度为1像素的骨架图像信息。在原图像/拟合图像面积比保持一致的前提下，调整圆心在骨架上均匀分布，最后可以得到炭黑聚集体的拟合图像。轮廓骨架算法流程如图2所示。

图2 轮廓骨架算法流程Fig.2 Flowchart of contour skeleton algorithm

最大内切圆算法拟合炭黑聚集体形态采用非等径球形粒子填充管道的方法[16]，用符合炭黑原生粒子粒径范围内的圆形来填充已知轮廓。首先采用Canny算子（同轮廓骨架算法）提取图像轮廓信息，然后将轮廓闭合区域进行排序标号，再根据序号依次对于各闭合轮廓分区域进行最大内切圆填充。填充过程中，先根据轮廓信息获得轮廓内部点的范围，设边缘点信息为（xi，yi），依次计算边缘内每一点到最近边缘点的距离（D）：

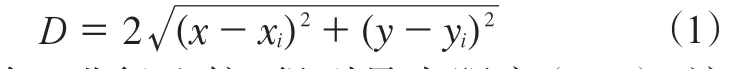
对所有D进行比较，得到最大距离（Dmax），该距离的一半对应的中心点就是最大内切圆的圆心。以该点为圆心，以统计粒径范围内的Dmax为直径画圆，进行分区域填充。之后在闭合轮廓范围中减去这一被填充的圆形区域，在剩余区域内继续重复求取最大内切圆，直至Dmax小于规定粒径为止。最大内切圆算法流程图如图3所示。

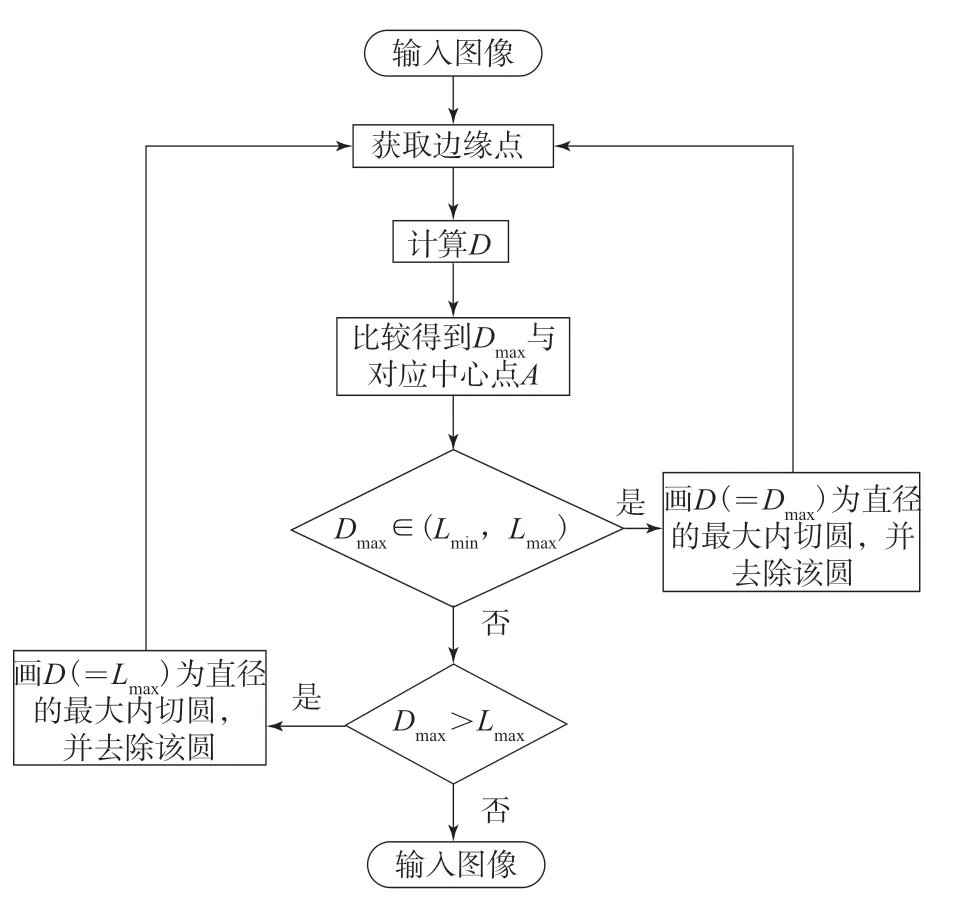
图3 最大内切圆算法流程Fig.3 Flowchart of maximum inscribed circle algorithm

根据灰度信息可采用K-means聚类算法拟合炭黑聚集体形态。先由橡胶复合材料电镜图像灰度直方图选取峰值点作为k个质心点，然后遍历图像中的所有像素点，计算图像中每个像素点（除质心点外）到全部质心点的距离，判断最小距离，将最小距离点归类为距离最小的质心点所在的簇。当2次循环的非质心点移动数量占总移动数量的比例（非质心点移动数量比例）的差值小于设定值时，确定峰值点最优，最后利用最小二乘法将k类像素点拟合为k个圆，再将所有圆进行颜色填充，得到拟合图像。靠近质心的部分重叠越多，颜色越深。K-means聚类算法流程如图4所示。

图4 K-means聚类算法流程Fig.4 Flowchart of K-means clustering algorithm

1.4 图像拟合效果评价

炭黑聚集体微观结构图像拟合效果采用标准峰值信噪比与结构相似度来评价。标准峰值信噪比是由原图像与拟合图像的均方误差而判定的，而结构相似度是由图像结构相似进行判定的，计算公式如下[17]：

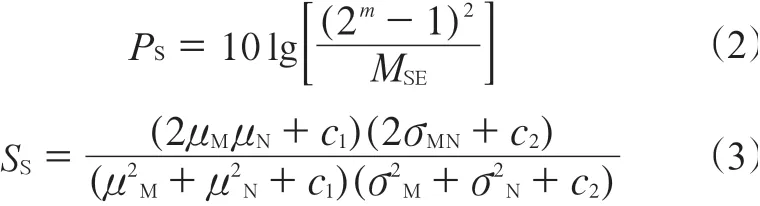
式中：PS为标准峰值信噪比；m为每个像素的比特数；MSE为原图像与拟合后图像的均方误差；SS为结构相似度；μM和μN分别为图像拟合前后的像素平均值；σM2和σN

2分别为图像拟合前后的像素方差；σMN为图像拟合前后的像素协方差；c1和c2为常数，c1＝（k1H）2，c2＝（k2H）2，H为像素的动态值范围（取255），k1和k2远小于1。

标准峰值信噪比越大，图像拟合效果越好，失真越少；结构相似度的取值范围为[0，1]，当图像完全不一致时为0，完全一致为1。

2 模型验证

取文献[18]中样品A和B的形态较复杂的炭黑聚集体电镜图像（见图5）进行3种算法拟合和对比。

图5 炭黑聚集体形态电镜图像Fig.5 Electron micrographs of carbon black aggregate morphologies

对样品A和B进行粒径标注。选取50组粒径数据进行统计，其中样品A的平均粒径为59.63 nm，取整为60 nm，样品B的平均粒径为35.12 nm，取整为35 nm；样品A和B的粒径范围频率分数偏差值分别为0.06和0.07，该值越小则表示粒径分布越均匀。炭黑粒径分布统计结果如图6所示。

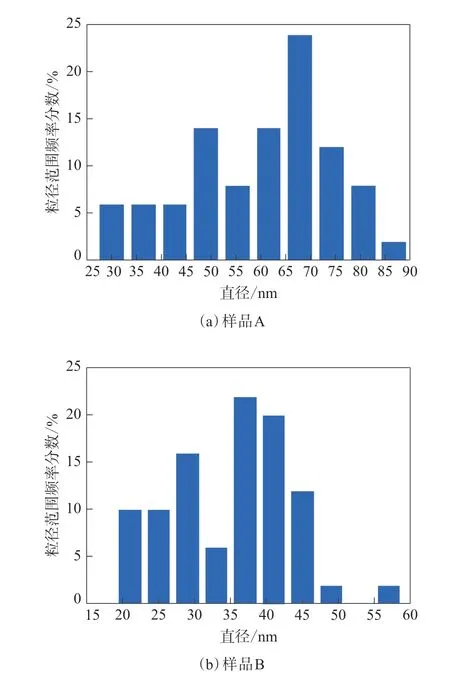
图6 炭黑粒径分布统计结果Fig.6 Statistical results of carbon black particle size distributions

从图6可以看出，样品A粒径约为样品B粒径的2倍，样品A粒径分布更均匀，图像处理结果与实际符合。

处理样品A和B的图像背景后进行阈值分割，并保留炭黑部分灰度值，结果如图7所示。

图7 背景处理后的炭黑聚集体阈值分割图Fig.7 Threshold segmentation graphs of carbon black aggregates after background processing

之后分别用轮廓骨架算法、最大内切圆算法和K-means聚类算法3种方法拟合背景处理后的炭黑聚集体图像。

（1）采用轮廓骨架算法拟合。考虑到灰度差异，将灰度图转化为二值图。用统计得到的炭黑原生粒子等径圆来拟合轮廓。为保证轮廓光滑，先使用粒径为2像素的圆形模板对二值图像进行形态学的膨胀处理；其次提取图像轮廓，再根据轮廓进行骨架化，使用统计原生粒子直径分别对样品A和B的聚集体轮廓画圆。轮廓骨架算法拟合结果如图8所示。

图8 轮廓骨架算法炭黑聚集体拟合图Fig.8 Fitting graphs of carbon black aggregates by contour skeleton algorithm

（2）采用最大内切圆算法拟合。先判定填充轮廓区域的最大内切圆直径以便确定拟合圆直径，当该最大内切圆直径在统计原生粒子直径范围内时，则其选作拟合圆直径；当最大内切圆直径大于统计原生粒子直径范围时，拟合圆直径选取原生粒子直径范围内最大值；当最大内切圆直径小于统计原生粒子直径范围时，忽略该内切圆。在聚集体轮廓内划分的各区域依次进行最大内切圆直径判断和确定填充直径并填充区域，反复重复以上过程进行迭代计算，直至剩余未填充部分的最大内切圆直径小于统计原生粒子直径范围为止。最大内切圆算法拟合结果如图9所示。

图9 最大内切圆算法炭黑聚集体拟合图Fig.9 Fitting graphs of carbon black aggregates by maximum inscribed circle algorithm

（3）采用K-means聚类算法拟合。先选取灰度最大值，然后将整图像素点进行分类，最后根据类别拟合成不同区域的圆形。K-means聚类算法拟合结果如图10所示。

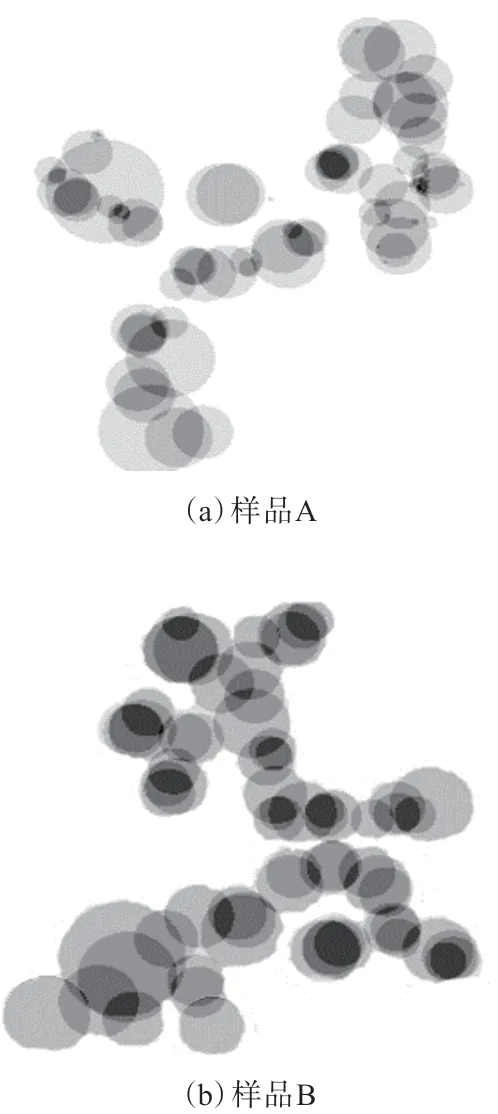
图10 K-means聚类算法炭黑聚集体拟合图Fig.10 Fitting graphs of carbon black aggregates by K-means clustering algorithm

从图10可以看出，炭黑聚集体形态大体如原图形状（存在的差异可能在于轮廓细节方面），其中每个圆的灰度值相同，但多个圆重叠后灰度值相加，就会出现图像中颜色深浅不一的效果，相加后的灰度值对应于原图中的灰度值信息。

为了比较3种拟合算法的效果，计算了标准峰值信噪比和结构相似度2个评价指标。3种拟合算法的评价结果如表1所示。

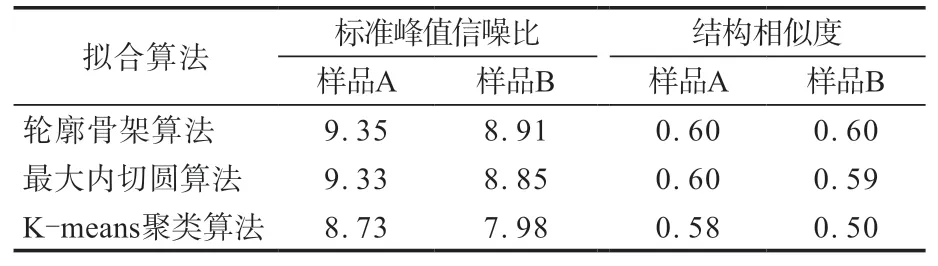
表1 3种拟合算法的评价结果Tab.1 Evaluation results of three fitting algorithms

从表1可以看出：采用标准峰值信噪比指标时，样品A的拟合效果优于样品B，而标准峰值信噪比取值范围比结构相似度更大；3种拟合算法精度从高到低依次为轮廓骨架算法、最大内切圆算法和K-means聚类算法，其中轮廓骨架算法和最大内切圆算法的2个指标值相差不大，考虑到炭黑聚集体由粒子堆叠形成，轮廓骨架算法为拟合炭黑聚集体形态的最佳算法。

3 结论

本工作采用图像背景处理、特征信息提取、粒径统计等方法进行了图像处理，研究了轮廓骨架算法、最大内切圆算法和K-means聚类算法3种图像拟合算法，并采用标准峰值信噪比和结构相似度指标对拟合效果进行评价，验证了炭黑补强橡胶复合材料微观图像重构建模方法的可靠性，结论如下。

（1）可以将原生粒子看作圆形以拟合炭黑聚集体形态，由统计方法得到的炭黑原生粒子直径及其分布范围可分别取为拟合圆直径及拟合圆直径范围。

（2）采用轮廓骨架算法、最大内切圆算法和K-means聚类算法可以拟合炭黑聚集体形态，经标准峰值信噪比和结构相似度指标评价，拟合精度从高到低依次为轮廓骨架算法、最大内切圆算法和K-means聚类算法。选用轮廓骨架算法描述炭黑聚集体形态的效果最好。

（3）标准峰值信噪比取值范围较大，结构相似度取值范围较小，2个指标对3种拟合算法的评价结果趋势较为一致。在图像拟合精度评价方面，结构相似度指标评判精度更高。