基于LTTB-KSC算法的网络舆情事件热度高峰研究
高 烨 李 松 郭海玲 李紫萱
(河北大学 管理学院 保定 071002)
0 引 言
互联网技术的飞速发展,使得越来越多的人通过网络来发表见解、公布消息以及获得热度,互联网上的信息呈现爆炸式增长,互联网迅速发展成为资源共享的平台。现实生活中的某些事件发生后,随着该事件在网络上发酵,会引起民众激烈的讨论,引发网络舆情。民众在关注该事件的同时,也会产生一些新的衍生话题,如果无法进行及时的处理,随着进一步的传播讨论,将会影响到民众的认知和社会的稳定。因此,研究网络舆情事件热度高峰将有助于相关部门预估民众对网络舆情事件关注程度的高峰期,及时监测可能出现的衍生话题,抑制负面言论,正确引导社会的舆论方向。
由于旧话题的消失或新话题的产生,网络舆情事件的发展在时间维度上是稳定的[1]。目前大多数的研究集中于热度的整体趋势,很少关注网络舆情事件热度曲线的峰值数据和特征,缺乏预测热度高峰期时间范围的科学方法。对热度趋势相关研究进行梳理,发现网络舆情事件的热度时间序列蕴含着丰富的时态信息,民众对相同类别事件的关注程度及其发展趋势在很大程度上具有相似性[2]。基于此,本文从聚类入手对热度高峰展开研究。K-Means算法和KSC算法是对时间序列聚类的主要算法,其中KSC算法根据时序的趋势特征进行聚类,能够刻画出时间序列之间的内在规律特征,对时间序列聚类效果更好。但是KSC算法也存在着一些缺陷:a.KSC算法的时间复杂度很高;b.初始类别中心选择很敏感,初始类别中心选择的好坏影响聚类的收敛速度;c.无法自动设定与调整聚类个数。
LTTB(Largest Triangle Three Buckets)算法是一种能够保持原始时间序列趋势特征的降维算法,将LTTB算法与KSC算法组合,使用LTTB算法对时间序列进行降维,然后使用KSC算法对降维后的数据聚类,能够改善KSC算法时间复杂度高和初始类别中心选择敏感性的问题。基于上述思想,本文提出了LTTB-KSC算法,据此构建出网络舆情事件热度高峰变化模式,并对网络舆情事件热度高峰期时间范围预测展开进一步研究。
1 相关研究
1.1 热度序列聚类研究
热度序列聚类是一种根据热度时间序列所呈现出的趋势和特征进行聚类的一种方法,它将具有相似趋势形状的热度时间序列聚集在一起,其聚类结果能够刻画出用户对某种话题或者某类事件关注程度的共同变化趋势,为网络话题或事件的热度预测奠定了基础。Yang等人[3]提出KSC算法对话题的热度时间序列进行聚类,定义了新的时间序列差异度公式和更新矩阵中心公式,以便刻画热度发展趋势的内在规律特征,但KSC算法在初始类别中心选择上非常敏感,且有高时间复杂度,不可直接将其应用于高维数据。韩忠明等人[4]针对KSC算法存在的缺陷选择用Haar小波变换对高维时间序列降维,然后在低维数据上进行聚类,虽有效解决了KSC算法初始类矩阵中心高敏感性、高时间复杂度的问题,但是每一层的降维是采用两个相邻值取平均值的方法,降维后的时间序列趋势特征丢失严重,低维度聚类结果较差,以此为依据确定出的高维初始矩阵中心会存在偏差,使得最终聚类结果存在一定误差。张茂元等人[5]使用集合经验模态分解(EEMD)对序列进行平稳化处理,得到具有物理意义的各个IMF分量,然后从低频分量开始聚类,将低频分量的聚类结果作为高频分量聚类的初始矩阵中心,有效地减少了非平稳特性对算法准确性的影响,但是在分解过程中会存在残余的白噪声,同时低频分量相较于原始时序也存在趋势特征缺失的问题,从而影响聚类结果。学者们对于KSC算法的改进取得了明显成效,但对原始时间序列的处理会使其丢失部分趋势特征,得到的聚类结果从波峰变化趋势来看具有一定的重合性,而且目前没有一个科学的方法能够自动设定与调整聚类的个数。
1.2 热度趋势研究
在热度趋势的研究中,学者们多通过挖掘自身历史数据对事件未来热度趋势进行预测。卢珺珈等人[6]通过发帖量衡量事件热度,采用高斯模型对帖子的发展态势进行拟合,在此基础上对帖子的热度在未来某时间段处于上升或下降作出预测。周西平等人[7]选取新浪微博上的热点事件,运用马尔可夫分析方法建立网络舆情热度趋势模型,预测事件所处的发展阶段。杨茂青等人[8]基于随机森林(RF)算法建立突发事件网络舆情演化预测模型,通过高效的定量预测模型预测未来某时间点的全网发帖量。学者们采用不同方法进行事件热度趋势的预测研究,但很少将目光集中于事件热度曲线的峰值数据和特征,缺乏预测事件热度高峰期时间范围的科学方法。
2 基于LTTB-KSC算法构建热度高峰变化模式
2.1 KSC算法
KSC(K_Spectral Centroid Clustering)算法是一种类似于经典K-Means聚类算法的迭代算法,它将时间序列的趋势特征作为聚类的依据,不考虑时间序列的具体幅值[9]。
KSC算法可分为类别划分和更新聚类中心两个步骤。首先,随机对所有时间序列进行分类,使用矩阵中心计算公式计算出每个类别的矩阵中心,使用差异度计算公式计算所有时间序列与每个类别矩阵中心的差异度,将时间序列归到差异度最小的类中;其次,根据划分到每个类的时间序列更新类别的矩阵中心。通过不断迭代,最终得到k个聚类结果。KSC算法是一个迭代的过程,迭代停止的条件是:每个类别的成员不再发生变化或者达到预定的迭代次数。
a.差异度公式。
(1)
式中,x和y表示两个时间序列,时间序列是按照一定的时间间隔排列的一组数据,时间间隔可以是任意的时间单位。每个时间序列表示{t1,t2,…,tL},L为时间序列的维度,ti可以表示事件每小时的热度值。yq是时间序列y移动q个时间单位的结果,平移后的时间序列y与x的峰值处于同一时间点。‖·‖表示向量范数,α为缩放系数,用α来匹配两个时间序列的形状。式(1)表明任意两个时间序列的相似性只与它们的趋势走向有关,而和它们的峰值数值以及在何时达到峰值无关[5]。
b.更新矩阵中心公式。
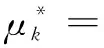

(2)
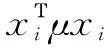
(3)
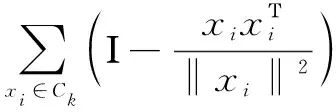
(4)
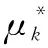
2.2 基于LTTB-KSC算法聚类
KSC算法将时间序列的趋势特征作为聚类依据,不考虑时序的具体幅值,能够挖掘出类似事件发展趋势中蕴含的规律,其聚类结果能够直接反映同类舆情事件的传播状态。但KSC算法也存在着一些问题:a.KSC算法的时间复杂度很高。对于N个L维的时间序列,算法迭代过程中每次需要进行N×L3次的差异度计算。b.初始类别中心选择很敏感。初始类别中心选取的优劣关系着聚类的收敛速率,如果初始类别中心选择不恰当,聚类的收敛速率将很低。c.无法自动设定与调整聚类个数。现如今聚类个数通常是根据历史经验获得或者利用仿真实验不断调整,而在海量数据下使用KSC算法时,如何针对时间序列的数据特点,自动选择并调节聚类个数,是亟待解决的问题。本文基于KSC算法存在的问题提出了LTTB-KSC(Largest Triangle Three Buckets-based KSC Algorithm)算法。LTTB-KSC算法聚类分为两个步骤:使用LTTB算法对原始时间序列降维;对降维后的时间序列聚类。
LTTB算法是在2013年由冰岛大学的Sveinn提出,主要用来对大数据集,特别是时间序列进行降采样以实现可视化,可应用于数据简化和计算机视觉领域,具有极高的数据预处理价值[10]。例如,现在许多网站为用户提供查看交互式折线图的功能,互联网数据广泛,用户的计算机绘制折线图需要一些时间,如果数据在绘制前被合理地降采样,用户等待时间减少,且不会对折线图产生任何可观察的影响,节省带宽和时间,使用LTTB算法对数据降采样可满足这一要求。
研究表明,LTTB算法对时序数据的降维拟合效果显著,能够使用较少的点充分描绘原始时序数据形态的外轮廓特征,具有非常好的视觉表现,因此本文选择使用该算法对高维度的时间序列降维,LTTB算法基于最大有效面积对时序数据降维与拟合,具体过程:
a.按照阈值(返回数据点的个数)将原始时序数据划分为大小近似的段,第一段和最后一段只包含原始数据第一个和最后一个数据点。
b.遍历所有段,从第一段到最后一段,并从每个段中利用算法选择出最重要的F点。
如图1所示,该算法一次使用三段,从左向右进行,形成三角形左角的第一段的点始终固定为先前选定的点,形成三角形右角的点是第三段中的临时点,B点为当前段中存在的点。若B点与固定点A(先前选择的)和临时点C形成三角形的有效面积最大,选择B点作为当前段的F点,代表当前段内的所有点。
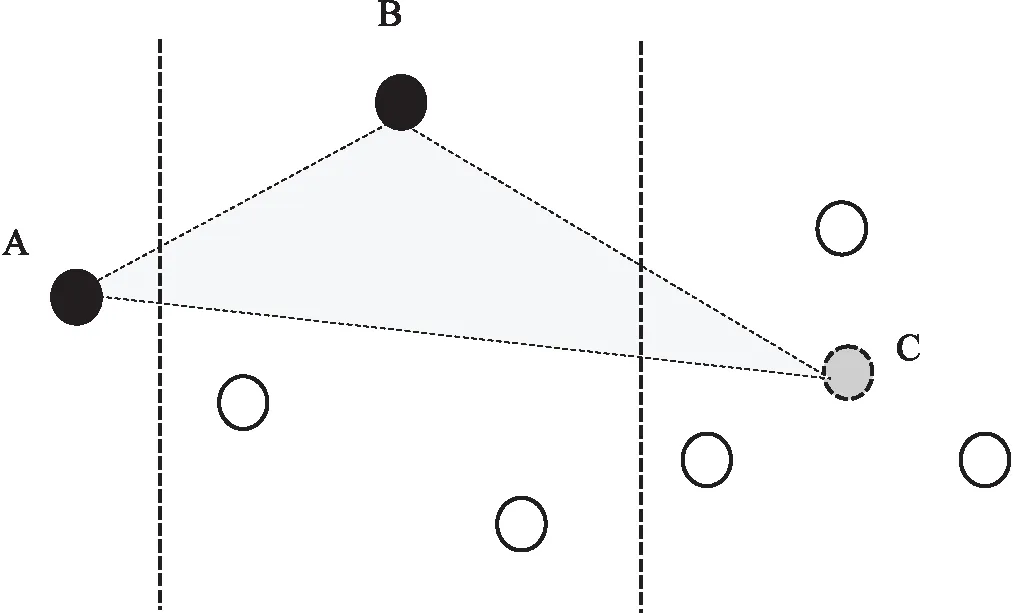
图1 LTTB算法F点的选择
临时点C的选择主要采用一种平均近似的虚拟固定点方法,假设某一段中有点集P={p1,…,pm}及虚拟固定点pv,每一点对应的值用val(pj)表示,则有
(5)
c.遍历完成后,将每一段中确定的F点组合成一个新的时间序列,即为降维后的结果。
利用LTTB算法对原始时间序列进行降维,能够保证降维后的时间序列仍完美保留着原始时间序列的趋势特征。对降维后的时间序列进行聚类,降低了时间复杂度,提高了聚类的速率。同时,对降维后数据进行初始类别的选择,计算初始类别矩阵中心,并以此为基础进行迭代,更新类别矩阵中心,也有效改善了KSC算法初始类别中心选择敏感性问题,LTTB-KSC算法具体构建流程如图2所示。
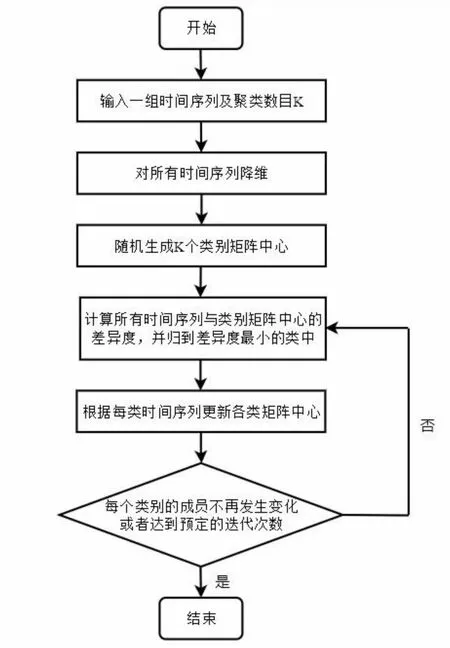
图2 LTTB-KSC算法构建流程
2.3 确定降维维度和聚类个数
2.3.1确定降维维度
构建网络舆情事件热度序列数据集通常需要收集长达一年甚至几个月的热度值,但热度时间序列所形成的热度曲线的体积往往集中在峰值附近,人们对于某个热门内容的关注程度仅维持一段时间,而在其它的时间里很少或者不会在提及,因此形成很长的时间序列是不合理的,需要对其进行截断。为了设定截断的长度,Yang等学者观测了事件流行程度扩散情况并进行了相应实验,实验结果表明可将热度序列的长度截断为128小时[3]。
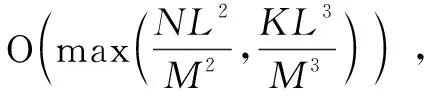
2.3.2确定聚类个数
已有文献多通过借鉴历史经验或者利用仿真实验不断调整聚类个数,直到聚类结果基本稳定,找到最佳聚类数。本文将聚类结果类间评价和类内评价相结合来确定最优的聚类个数。
采用F-Value(F值)刻画每个类内部成员的差异度,该值越小表示类内的元素越紧凑,聚类效果越好。使用KSC算法中的差异度公式来计算F值,具体公式为
(6)
采用D-value(D值)来衡量类别之间的差异性,类别之间差异越大,表明聚类效果越好,计算公式为
(7)
式中,μi代表类别i的矩阵中心,μj代表类别j的矩阵中心。
将F值和D值结合,寻找F/D的最优值。F值衡量类内成员聚类效果,越小越好,D值衡量类间聚类效果,越大越好,因此,希望找到最小比值对应的聚类数作为最佳聚类数。
(8)
2.4 矩阵中心曲线拟合
为精准拟合矩阵中心曲线,保证矩阵中心对应的时间序列维度与单位小时的一一对应,首先采用三次样条插值法将矩阵中心的维度扩展为原始时间序列的维度。三次样条插值是基于分段低次插值思想进行数据插值,目的是求出穿过原本给定的一系列点的分段三次多项式函数,并使得所有的点都保证至少二阶连续可导。得到全段的三次多项式函数后,就能计算出原数据点间的插值结果。
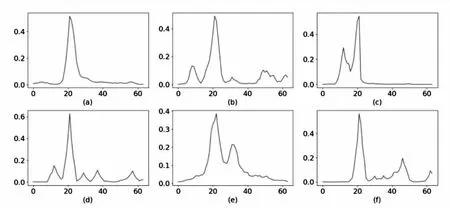
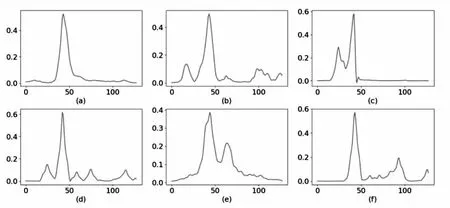
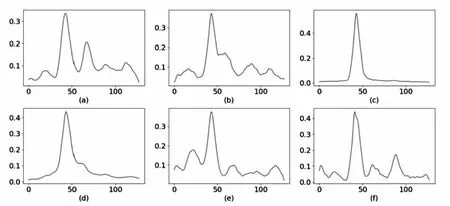
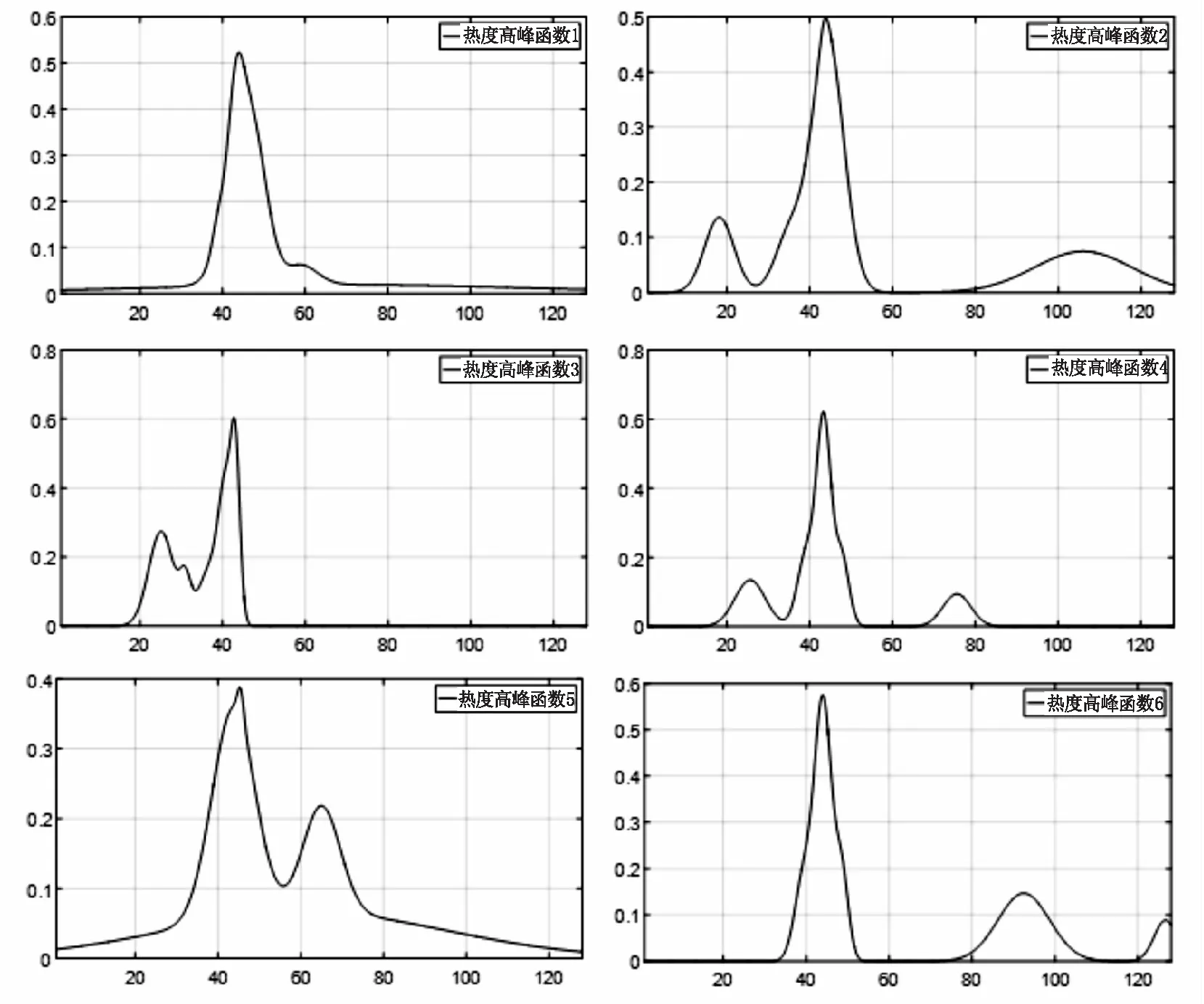
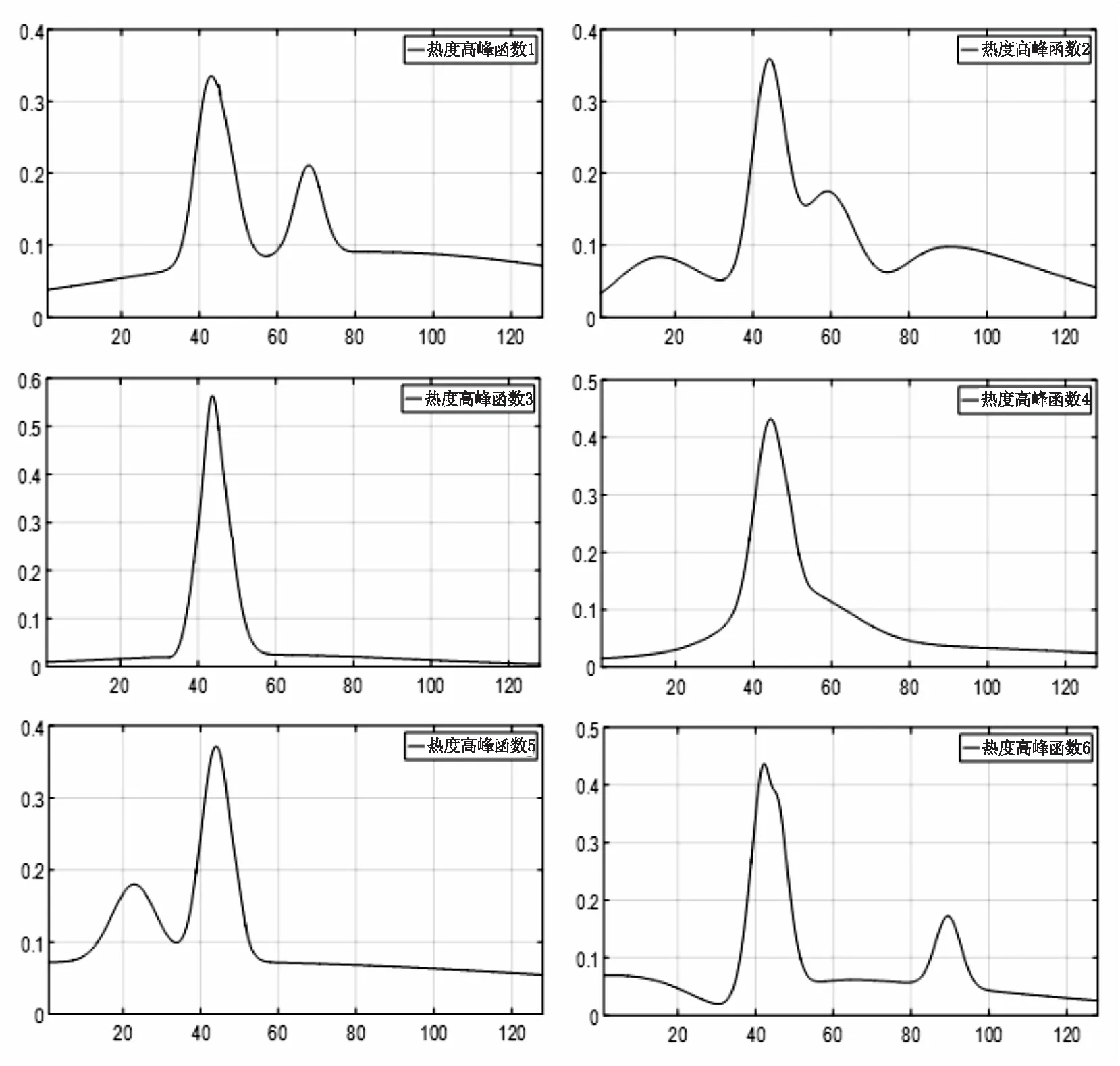
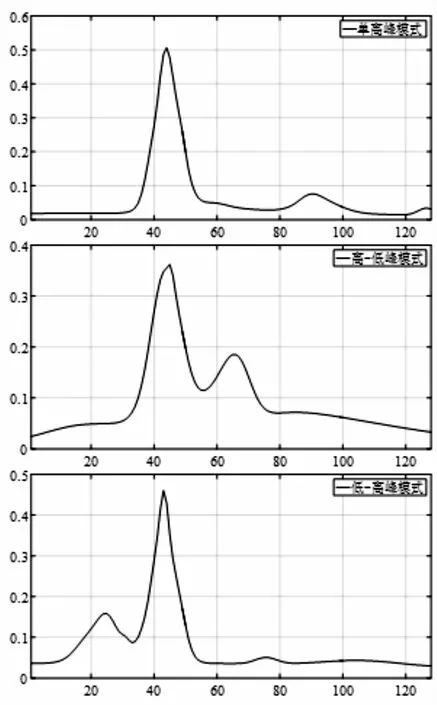
假设有节点x:a=x0 (1)在每个分段小区间上[xi,xi+1]上,S(x)=Si(x)都是一个三次多项式; (2)满足插值条件,S(xi)=yi; (3)曲线光滑,S(x),导数S′(x),二阶导数S″(x)连续。 n个分段三次多项式的形式为 Si(x)=ai+bi(x-xi)+ci(x-xi)2+di(x-xi)3,i=0,1,…,n-1 (9) 式中,Si(x)是第i+1个区间对应的三次方程;ai、bi、ci和di是三次样条方程的4n个未知系数。 采用三次样条插值法对聚类结果中每一类的矩阵中心建立分段三次多项式函数,并在原数据点间进行插值,将矩阵中心的维度扩展到原始时间序列相同维度,通过三次样条插值得到的插值点非常符合原数据点的变化特征,能够保证维度扩展后的矩阵中心曲线完整保留着原始曲线的变化趋势。 高斯混合模型是多个单高斯概率密度函数的线性组合,通过调整高斯混合模型的各个组成参数,包括成分数、权重系数、均值和每个成分的协方差矩阵,来精确描述各种概率密度分布[11]。通俗来说,无论观测数据集如何分布以及呈现何种规律,都可以通过多个单一高斯模型的混合进行拟合[12]。因此本文选择使用高斯混合模型拟合扩展维度后的矩阵中心曲线,得出每一类的热度高峰函数。 高斯混合模型通常被用来对多维随机变量的联合概率密度函数建模[11],可表示为 (10) 式中,φ(x|θk)表示高斯分布的概率密度函数,其表达式为 (11) 设需要n个高斯分布拟合聚类结果的矩阵中心曲线,则每一类的热度高峰函数为 (12) 构建热度高峰变化模式分为五个步骤。 a.按一定的时间间隔从网络平台上爬取网络舆情事件热度序列数据集,数据集中包含N个热度序列。 b.将N个热度序列使用LTTB-KSC算法进行聚类。首先使用LTTB算法降维,然后使用KSC算法对降维后的时间序列聚类,最终得到聚类结果{C1,…,Ck},每一类别Ci由热度序列{y1,…,ym}组成,m代表该类别中包含的热度序列的个数。 c.采用三次样条插值法将每一类矩阵中心扩展到原始维度(L维)。聚类结果中每一类别的矩阵中心表示该类成员的共同形状特征,类别Ci的矩阵中心表示为{Z1,…,ZH},其维度为H维(H d.根据维度扩展后的矩阵中心曲线特征选择合适的高斯混合模型对扩维后的矩阵中心进行曲线拟合,得到每一类的热度高峰函数及函数曲线。 e.观察每一类热度高峰函数曲线,根据曲线的波形特征进行模式划分。将每类模式中所属的矩阵中心拟合值采用算数平均法求得热度高峰模式值,最终得到热度高峰变化模式曲线。 时间序列的相似性属于曲线相似性/曲线匹配领域的内容,判断时间序列相似性需要从距离和形状两方面考虑。要衡量距离和形状,欧式距离有着广泛的应用,但用欧式距离衡量时间序列的相似性存在着致命的缺陷:a.忽略序列的波动形态,不能辨别形状和反映趋势动态变化幅度的相似性[13];b.由于复杂时间序列的不确定性与突变性,易将其误判与简单的时间序列更相似,而不是同类复杂时间序列[14]。因此,引入动态时间规整算法(Dynamic Time Warping, DTW),DTW算法采用动态寻优的方法求解最小累计欧式距离,通过路径回溯寻找两个序列点间的最佳匹配,使用最小累计欧式距离(DTW距离)衡量两个时间序列的相似度。DTW算法弥补了欧式距离所有点直接对应计算的缺陷,而是寻找序列之间逻辑上正确对应的点进行距离的计算,有效地解决时间序列时间轴上的偏移和伸缩后相似性度量的问题[15]。 给定时间序列x={x1,x2,…,xm}和y={y1,y2,…,yn},x为参考序列,y为测试序列,使用DTW算法衡量时间序列相似性的具体过程如下: a.计算序列点之间的欧式距离,构成m×n的距离矩阵。 c(m,n)=‖xi-yj‖2 (13) b.构造累计距离矩阵D={r(i,j)}m,n (14) c.基于累计距离矩阵D,采用路径回溯方法,从矩阵右上角开始,向左下寻找一条弯曲路径W=(w1,w2,…,wk)使得路径经过的元素之和最小,x和y匹配度最大。 d.弯曲路径对应的值即为时间序列x和y的DTW距离,DTW值越大,距离越远,时间序列的相似度越小,反之亦然。 当新的网络舆情事件发生时,首先按照一定的时间间隔采集该事件的热度,获得该事件的热度时间序列;然后利用DTW距离计算新事件热度序列与每一类热度高峰变化模式值的相似度,将其划分到相似度最大的热度高峰变化模式中;最后将该热度高峰变化模式曲线对应数值按照已知实际热度值进行一定比例缩放,得到热度高峰趋势预测曲线,预测出网络舆情事件热度高峰对应的时间范围,具体步骤如下: a.按一定时间间隔采集新事件发生初期的热度,获得初期热度序列x,长度为len(x)。设每一类的热度高峰变化模式对应的热度序列为yi,长度为128,i的大小取决于热度高峰变化模式的数目。 b.使用DTW距离计算x与yi的相似度,将x划分到相似度最大(DTW距离最小)的热度高峰变化模式中,将该模式作为事件热度高峰趋势的预测模型。通常选取yi中前len(x)个数值参与距离的计算,但为保证结果的准确性,需考虑现实时序曲线与模式曲线之间可能存在的偏移误差,选取的yi的数值长度相较于len(x)需进行一定程度的延长,延长距离由模式曲线的趋势决定,设延长距离为d,最终选取yi中(len(x)+d)个数值计算DTW距离。 c.将选定的热度高峰变化模式曲线对应数值按照已知实际热度值进行一定比例缩放,得到网络舆情事件热度高峰趋势预测曲线。观察曲线趋势,定位曲线波峰位置,将每一维度转换为与之相对应的具体时间,最终获取网络舆情事件热度高峰对应的时间范围。 实验共使用三个数据集,前两个数据集来自Stanford大学的MemePhr和Twhtag数据集。MemePhr数据集选自博客和网站上的1 000个热门帖子和新闻,以每小时的评论数作为热度,维度为128;Twhtag数据集选自twitter上的1 000热门帖子,以每小时该话题被提到的次数作为热度,维度为128;第三个数据集是从新浪微博平台采集的2021年11月30日3时到12月5日10时网友关于“失联摄影师鹿道森确认死亡事件”所发表的博文内容,共计3 714条,统计每小时网友发表的博文数量作为该事件每小时的热度。本文基于前两个标准热度时间序列数据集和“鹿道森事件”相关数据进行实验研究。 通过进行对比实验,不断调整降维维数,结果表明当热度序列降到一半维度(64维)时,降维后的热度序列比较完整的保留着原始热度序列的趋势和特征。部分对比结果如图3所示。 图3 不同维度时间序列曲线图 通过实验寻找最佳聚类数,选取F值与D值的最小比值,实验发现结果不停下降,从k=6开始导数趋于0,F/D最小且不再改变,则确定最佳的聚类数(k=6),结果如图4所示。 图4 F与D的比值结果 为验证提出的LTTB-KSC聚类算法的有效性,对KSC和LTTB-KSC算法从聚类效率和聚类效果两方面进行比较。 a.效率比较。对比KSC和LTTB-KSC算法在MemePhr和Twhtag数据集上进行聚类所消耗的时间,结果如图5所示,时间单位为s。 图5 两个算法在不同数据集下的消耗时间结果 从图5中可以看出LTTB-KSC算法在聚类时间上相较于KSC算法有了明显的改进,LTTB-KSC算法在MemePhr数据集上进行聚类的时间相较于KSC算法减少了将近35%,在Twhtag数据集聚类的时间减少了将近21.5%。 b.效果比较。衡量一个聚类算法的优劣,不仅要考虑使用该算法进行聚类的效率,还要考虑聚类结果是否合理,本文用F值(公式6)和D值(公式7)从类内和类间两方面评价聚类结果的合理性。表1给出了KSC算法及其组合算法在两个数据集上聚类结果的F值和D值,对比表内数值可以看出LTTB-KSC算法的聚类结果在类内成员紧凑程度和类间差异性上都要优于KSC算法,原因在于LTTB-KSC算法对原始热度时间序列进行了降维,降维后的热度序列比较完整的保留着原始热度序列的趋势和特征,然后在低维数据上计算出每个类的初始矩阵中心,则优化了初始类别矩阵中心的计算结果,并以此为基础进行迭代,更新每个类别矩阵中心,能有效改善KSC算法初始类别中心的敏感性问题。 表1 两个算法在不同数据集下的F值和D值 以MemePhr和Twhtag数据集中的热度时间序列为基础构建热度高峰变化模式。首先对数据集中的热度序列进行聚类,将热度序列按照变化趋势聚为6类,结果如图6和图7所示;然后采用三次样条插值法将每一类的矩阵中心维度从64维扩展到128维,结果如图8和图9所示。 图6 MemePhr数据集聚类结果的矩阵中心曲线 图7 Twhtag数据集聚类结果的矩阵中心曲线 图8 MemePhr数据集扩展维度后的矩阵中心曲线 图9 Twhtag数据集扩展维度后的矩阵中心曲线 观察每一类扩维后的矩阵中心曲线,根据曲线的趋势特征选择高斯混合模型来对其进行曲线拟合,得出热度高峰函数。每一类的热度高峰函数曲线如图10和图11所示。 图10 MemePhr数据集下每一类热度高峰函数曲线 图11 Twhtag数据集下每一类热度高峰函数曲线 根据每一类矩阵中心曲线特征,选择使用5个高斯分布对其进行曲线拟合,得到的热度高峰函数具体公式为 (15) 观察每一类热度高峰函数曲线图,曲线多呈现单峰和双峰特征,结合曲线趋势可将人们对网络舆情事件关注程度的曲线高峰划分为三大变化模式,如表2所示。 表2 热度高峰变化模式 a.单高峰模式。事件一经发生迅速引起广泛关注,热度达到最高峰,当公众事件得到处理或者满足人们的好奇心后,互联网出现的海量新话题转移了人们的注意力,人们对该事件的关注程度迅速衰减。 b.高-低峰模式。事件一经发生引起广泛关注,热度急剧上升达到最高峰,事件进入衰退期后,当与事件相关联的消息发布时,会再次引起人们对该事件的关注,引发热度波动。 c.低-高峰模式。事件发生初期并没有引起广泛关注,热度呈现小幅度波动,随着事件发酵到一定程度,人们对事件的关注程度急剧攀升,热度达到最高峰。当事件进入衰退期后,会出现两种情况,一是热度衰减为0,人们不再关注该事件;二是当相关联事件或话题出现后,再次引发该事件的热度波动。 在热度高峰时间范围的预测中,主要关注的是峰值数据和特征以及对应的时间范围,因此根据每一类热度高峰函数曲线的波形特征将其划分到相应的热度高峰变化模式中,划分结果如表3和表4所示。 表3 MemePhr数据集热度高峰模式划分 表4 Twhtag数据集热度高峰模式划分 根据两个数据集的模式划分结果,使用算数平均法整合热度高峰函数曲线具体数值,最终得到热度高峰变化模式曲线如图12所示。 图12 热度高峰变化模式曲线 根据网络舆情事件热度高峰变化模式,预测新舆情事件热度高峰变化趋势。根据采集的“鹿道森事件”的数据,将媒体通报失联摄影师鹿道森确认死亡前32小时内(11月30日3时到12月1日10时)每小时事件的热度作为训练数据,构建初期热度时间序列。然后利用DTW距离计算“鹿道森事件”初期热度序列与每一类热度高峰变化模式值的相似度,通过对比事件初期热度序列与每一类热度高峰变化模式曲线趋势,确定参与计算的热度高峰变化模式数值相较于初期热度序列延长5个单位,最终计算结果显示与高-低峰模式的相似度最大,将高-低峰热度高峰变化模式作为“鹿道森事件”的预测模型,根据训练数据将预测模型的数值放大500倍,得到“鹿道森事件”热度高峰趋势预测曲线,结果如图13所示。 图13 “鹿道森事件”热度高峰趋势预测对比 根据“鹿道森事件”热度高峰趋势预测曲线,捕捉峰值特征,将小时数转换为具体时间,转换结果如图14所示,精确定位事件热度高峰对应的时间范围。图中矩形虚线框部分对应的时间范围为12月1日中午12点到12月3日上午7点,这段时间即为预测的“鹿道森事件”热度最高的时间范围。 图14 “鹿道森事件”热度高峰时间范围 从图13和图14对比结果可知,“鹿道森事件”热度高峰趋势真实曲线与预测曲线外轮廓大体相似,虽然预测热度值和真实热度值存在一定偏差,但预测曲线能够反映出真实曲线趋势变化,突出波峰特征,根据预测曲线定位的“鹿道森事件”热度高峰时间范围与真实热度高峰时间范围大致重合,结果理想。 本文为进行网络舆情事件热度高峰时间范围的预测展开了一系列研究和实验,首先对热度序列聚类方法和热度趋势研究进行了梳理和总结,针对KSC算法的优缺点,提出了LTTB-KSC算法以及科学合理的聚类数目确定方法。在MemePhr和Twhtag数据集上进行实验,实验结果表明LTTB-KSC算法在聚类效率和效果上都优于KSC算法。然后借助三次样条插值法和高斯混合模型构建每一类的热度高峰函数,通过分析热度高峰函数曲线将热度高峰的变化情况分为单高峰、高-低峰和低-高峰三种模式。最后使用DTW距离判断网络舆情事件所属的热度高峰变化模式,得出热度高峰趋势曲线,定位热度高峰对应的时间范围。本文所构建的热度高峰变化模式将有利于相关部门及时采取不同措施控制舆论导向,维护社会和谐稳定。 本研究在构建热度高峰变化模式时还存在一些问题,每个热度高峰变化模式对应数值采用算数平均法求得,最终结果会弱化曲线部分趋势特征,后续会考虑采用更为合适的方法求解热度高峰变化模式值,使热度高峰变化模式曲线更具有代表性。此外,在未来的研究中将根据本文所提出的方法及时定位网络舆情事件热度高峰时间范围,采集民众在该时间段内对事件的讨论内容,监测网络舆情事件可能产生的衍生话题。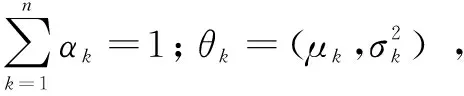
2.5 热度高峰变化模式构建流程
3 网络舆情事件热度高峰时间范围预测
3.1 DTW距离衡量时间序列相似度
3.2 高峰时间预测
4 实验与分析
4.1 实验数据
4.2 确定维度和聚类数目
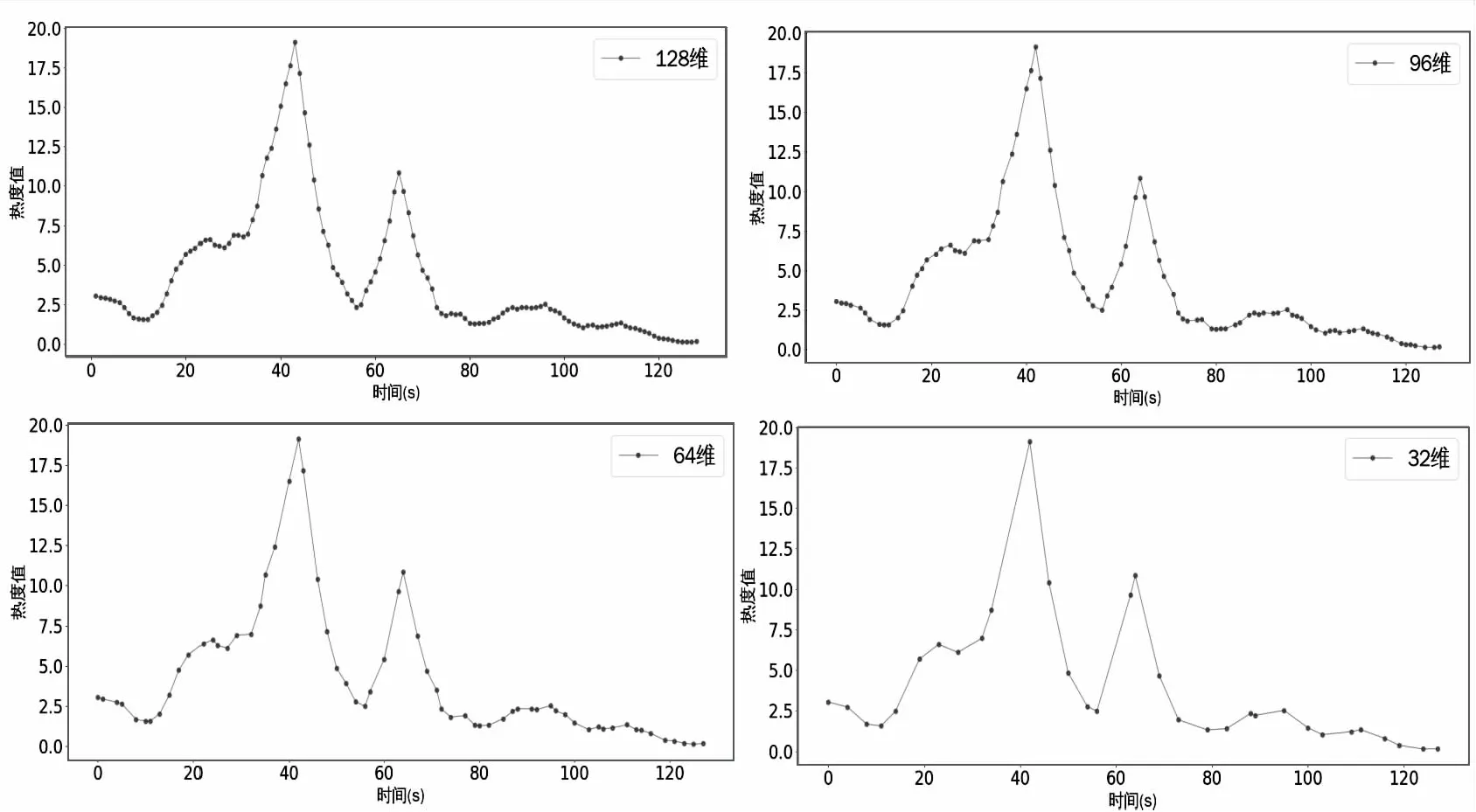
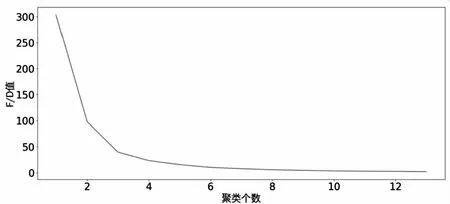
4.3 算法聚类结果比较
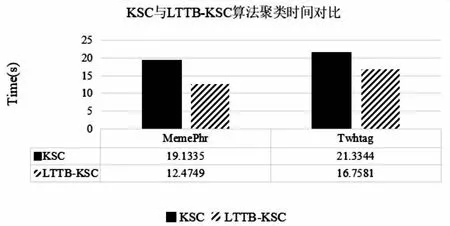
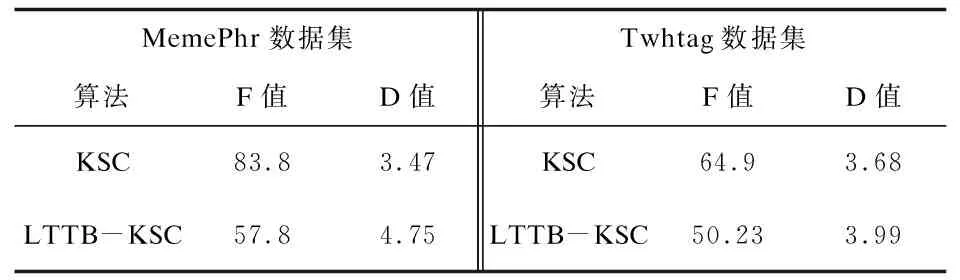
4.4 构建热度高峰变化模式




4.5 热度高峰时间范围预测
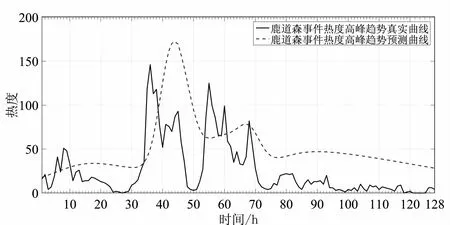
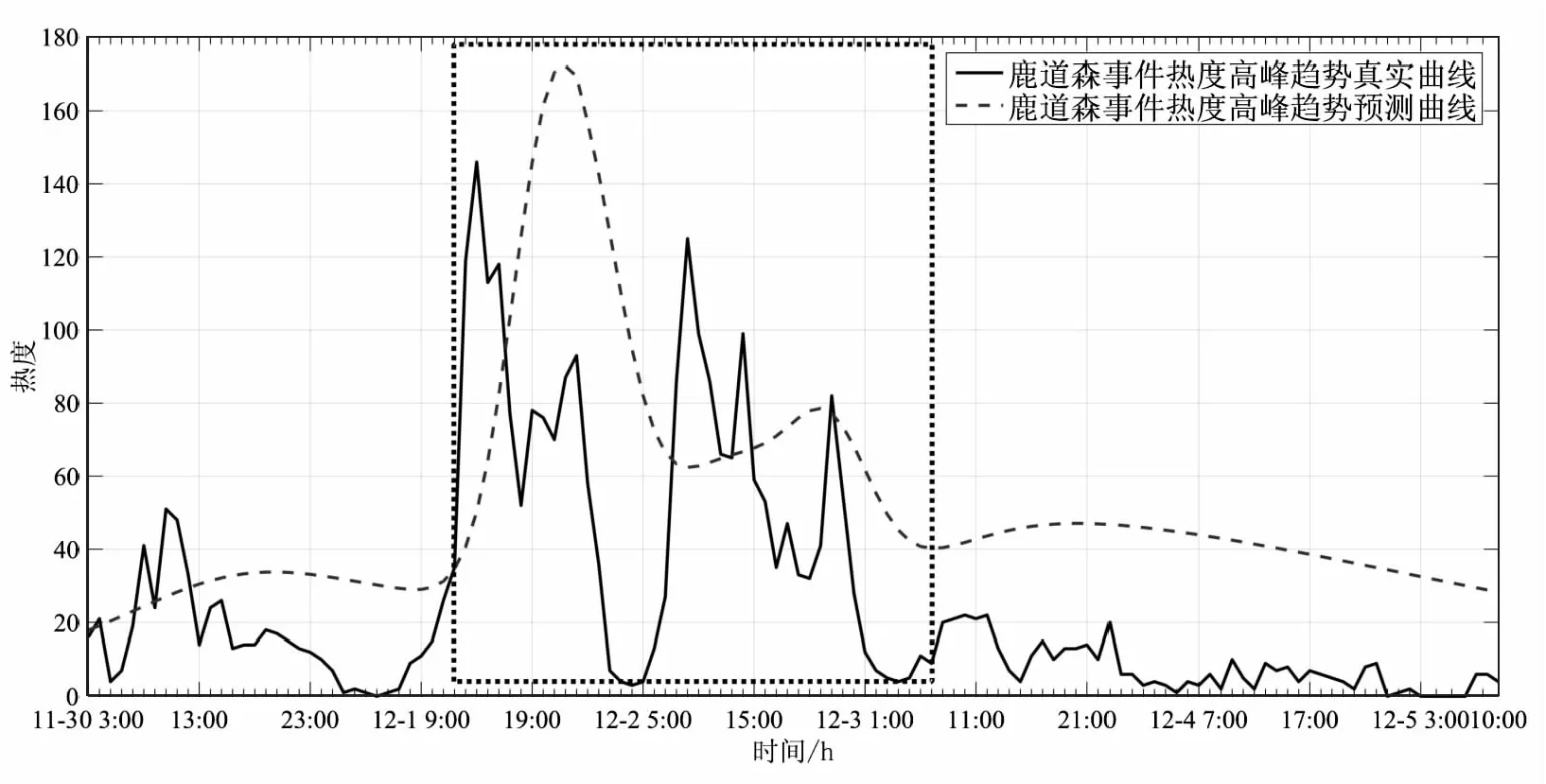
5 结 论

