初中数学教学中数形结合思想的应用

山东省淄博市桓台县实验学校 于国丽

山东省淄博市桓台县实验中学 刘 妍

一、初中数学教学中数形结合思想的应用价值

第一，可以助力学生更好地理解数学知识。数学知识抽象性强，尤其是一些数学概念，不仅抽象而且有很强的概括性，学生理解起来吃力。教师在课上若是渗透数形结合思想，以直观形象的图形将其表现出来，可以明显降低学生理解难度，还能加深学生对这些基础知识的理解与记忆，有利于后面学习中的迁移应用。

第二，可以提升学生的思维能力。数形结合思想的应用涉及“数”与“形”的转化，学生在面对几何图形时要深入挖掘其中隐藏的数量关系。同样，在面对代数知识时思考如何通过几何图形使其直观呈现。这个过程需要空间想象、逻辑思维、发散思维、创新思维的参与，所以有助于提升学生思维能力。

第三，可以增强学生问题解决能力。在数学中，“数”与“形”是两个重要元素，学生若是能巧妙地处理这两者之间的关系，灵活转化，就能轻松解决数学中的大多数问题。此外，数学思想方法从本质上来说就是解题思路、方法的凝练，数形结合思想也是如此。学生在数学学习中会用数形结合思想，就可以触类旁通、举一反三，解决数学问题会更加轻松，正确率也会更高。

二、初中数学教学中数形结合思想的应用策略

（一）数形结合思想的应用形式

1.以形促数

顾名思义，“以形促数”是指通过几何图形促进学生对代数知识的理解，这是数形结合的常见形式之一。初中数学中包含很多复杂的内容，如抽象的数量关系，教师可以通过图形直观地呈现出来，从而降低学生理解难度。

以“一次函数”教学为例，一次函数的方程式是“y＝ax+b（a≠0）”，a、b均是常数。如果教师直接解释数量关系，学生难以理解，若是教师用直观的图形呈现这个函数中的数量关系，学生就能轻松且深入地理解。在教学实践中，教师可以通过板书或者多媒体的形式给学生展示以下图形，结合直观图形去解释一次函数中的数量关系（如图1所示）。

有了这样的图形作支撑，教师就能轻松给学生讲解一次函数的知识。在教学实践中，教师将主动权交给学生，让学生阐述自己从这些图形中获得的信息。

学生1：我发现a的正负决定了直线的倾斜方向。

学生2：我发现a的大小决定了直线的倾斜程度。

学生3：我发现b的正负决定了直线与y轴交点的位置。

……

原本抽象且复杂的一次函数知识，经过图形直观化处理后，学生轻松理解，不仅知道了一次函数是什么，对一次函数的性质也有了深刻、全面的认识。

2.以数解形

顾名思义，“以数解形”是指通过数量关系解析图形内容，是“以形促数”的对立面，通常运用在对复杂图形的认知与解析上。具体来说，当讲解复杂的图形或者当学生在学习中遇到复杂的图形时，教师可以引导学生用定量计算的方式处理，巧妙地论述题型中所隐藏的条件，以此计算图中相关内容。

通常来说，在几何图形解析中，教师可以尝试运用“以形促数”思想。如图2所示，图形是由四个全等的长方形构成，中间空白区域利用已知条件列出等式。

图2 几何图形例题图

已知图2中的四个长方形全等，所以中间区域是边长相等的正方形，可以用数量关系表示该正方形的边长为a-b。由正方形面积公式可知，该图形的中间面积是（a-b）2。再从另一个视角解析这其中的数量关系，整个大的图形是边长为a+b的正方形，其面积是（a+b）2，而中间区域的小正方形面积是大正方形面积减去四个全等长方形，即（a+b）2-4ab。这样就可以得到恒等式（ab）2＝（a+b）2-4ab。

（二）数形结合思想的应用途径

1.应用数形结合思想讲解基础知识，加深学生的理解与记忆

基础性知识尤为重要，只有当学生对这些数学概念、公式、规律、定理等知识形成深入、全面的认识时，才能奠定牢固的基础。而巧妙地运用数形结合思想，可以解决学生学习难、理解不透彻等问题。换言之，教师在讲解数学概念、公式、定理等基础知识时，若能运用数形结合思想，对其直观化处理，可以化难为易，将晦涩难懂的知识变得通俗易懂，还能加深学生的理解与记忆。

例如，很多学生不理解“绝对值”的概念，所以在做题时经常出错。如面对“求a（a＜0）的绝对值”这道题时，很多学生直接得出答案“a”。为了让学生充分理解，教师可以利用数轴去讲解（如图3所示）。

图3 数轴

通过数轴的直观呈现，学生深刻地理解绝对值表示的是数轴上某个点到原点的距离。数轴上原点右边1.5的点到原点距离是1.5，原点左边-1.5的点到原点距离也是1.5。同样，原点右边4的点到原点距离是4，原点左边-4的点到原点距离也是4，即绝对值不会是负数，而是一个正数。清楚地理解并掌握绝对值概念后，学生在面对“求a（a＜0）的绝对值”这道题时就能轻松地得到答案“｜a｜＝-a”。

2.应用数形结合思想优化解题方法，提升学生问题解决能力

在初中数学教学中，解题教学是核心内容，占据重要位置，也是学生学习数学的难点所在。尤其在面对复杂的数学问题时，很多学生往往束手无策，不知道从哪里着手。教师可以渗透数形结合思想，这不仅可以让学生学会解当前的数学问题，更重要的是，学生可以通过数形结合思想学会解决这一类题。

例如，初中数学的“最值”问题让很多学生在处理时束手无策，很多学生缺乏科学、有效的方法，不仅解题效率低，而且解题正确率也非常低。为了提升学生解决这类题的能力，教师可以渗透数形结合思想。如这样一道题：已知x+y＝6，x、y均大于0，问的最小值。很多学生面对这道题时往往找不到突破口，若是按部就班地用代数方法求解，不仅烦琐复杂而且正确率低。这种情况下，教师可以引导学生运用数形结合法，将抽象的代数问题转化为形象的几何问题。通过勾股定理，可以将看成两个直角三角形的斜边，而且这两个直角三角形在一条线上，如图4所示。

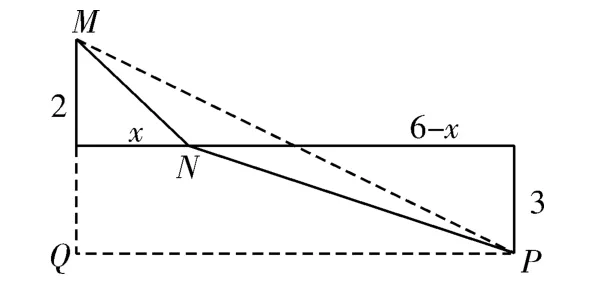
图4 根据勾股定理绘制的直角三角形

通过图形可以直观看出，只要求出大三角形MPQ的斜边，这个代数问题就能迎刃而解。而根据勾股定理可以轻易得到。由此可见，原本复杂难解的问题经过转化后变成难度系数较小的求勾股定理斜边问题，教师在解题时应给学生强调这一点，以此培养学生的数形结合意识，让学生认识到数形结合思想的力量并养成运用数形结合方式解题的良好习惯。

三、结语

综上所述，在初中数学教学中应用数形结合思想可以让学生更加直观、清晰地了解并掌握数学知识，从而减少学生在数学理解与认知上的困难。同时，合理地渗透数学思想方法可以拓宽学生思维空间，在提升学生解题能力的同时使其养成良好的学习习惯。在教学实践中，教师应在基础知识讲解、数学问题讲解这两个主要环节中有效渗透“以形促数”与“以数解形”思想，切实有效地提升学生的数学学习水平，同时达到减轻学生负担的目的，贯彻落实“双减”政策。