绝缘子智能水冲洗装置伺服驱动系统动态性能研究

曾鑫鹏， 吴文海， 廖国庆， 程渊海， 毛定邦

(1.西南交通大学机械工程学院， 四川成都 610030；2.中国铁路济南局集团有限公司青岛供电段， 山东青岛 266071)

0 前言

轨道交通中的绝缘子是隔绝载流导体与地面、保证铁路系统用电安全的重要部件，由于环境的影响，绝缘子表面时常会附着污渍。MAOWED和MOUSSA[1]曾研究过不同污染条件下，绝缘子的性能变化，污渍的积累会导致绝缘子发生污闪事故，这已成为电气化铁路中的危害之一。为了避免污闪事故的发生，需要定时对它进行清洗工作。

在工业控制中，随着自动化技术的发展，智能设备逐步代替了人工，但在一些对装置精度及稳定性具有较高要求的场合，却仍在使用人工操作。例如轨道交通中绝缘子的冲洗工作，由于冲洗流程较严格，国内外仍以手动控制冲洗为主[2]，这不仅降低了冲洗效率，还存在一些安全隐患，因此，展开对绝缘子智能水冲洗装置的研究具有工程应用价值。

为了提高绝缘子水冲洗装置的精确性与稳定性，可从机械结构与伺服控制2个方面分析其中的影响因素。对于机械结构，YAN等[3]完成了立式绝缘子清洗机器人的构型设计，并检测了运行效果，但缺少实物模型的搭建与验证；在智能控制方面，王奇等人[4]提出了一种基于图像伺服的绝缘子自动水冲洗车，并通过仿真模型验证了视觉伺服的可行性；对于振动特性的分析，张洪等人[5]提出了一种设计和优化油罐喷涂机器人振动特性的方法，对于绝缘子冲洗装置的平稳性优化具有一定参考价值，但其振动优化仅局限于结构；刘洋等人[6]对柱塞泵的振动机制进行了研究与分析，提出了对于径向柱塞泵的力学优化方案；黄海鹏等[7]还通过将高压喷水技术与无人机结合，研发了一种可远程控制的冲洗无人机，但因储水量受到限制，仅适合小型化清洗。钱博[8]对于机械装置中非线性动力学问题的研究为文中的结构动力学分析提供了简化力学模型的思路。

在现代智能控制中，以永磁同步电机(PMSM)为控制对象的交流伺服系统正被广泛地应用[9-11]，许多场合对其系统的响应性以及稳定性有着很高的要求。赵云等人[12]所提出的一种通过内模控制(IMC)观测器来补偿振动速度信号的方法为优化文中的伺服控制提供了新的借鉴方法，但却仅限于理论与仿真研究。

文中研究以PMSM为对象的交流伺服控制系统，将它应用在绝缘子水冲洗工作中，从而设计并分析绝缘子智能水冲洗装置的机械性能，并运用时变速度环增益系数的优化方案；通过结构建模与实验仿真，验证优化方案的有效性；最后，在实体装置实验中，检测此方案对系统振动特性的影响。

1 绝缘子智能水冲洗装置

根据国内外已有的冲洗设备，引入伺服驱动系统以及伺服电机，通过上位计算机的智能算法以及双目摄像头的图像采集，可完成轨道交通中绝缘子的智能识别与定位工作，文中对冲洗装置的传动结构进行了设计，并结合高压水冲洗的射流技术，在已成熟的液压冲洗系统的配合下，设计出了一种绝缘子智能水冲洗装置。

图1所示为智能绝缘子水冲洗系统的组成原理，该系统由机械传动模块、伺服控制动力模块以及液压冲洗模块三部分组成。机械传动模块包含回转模组与俯仰模组，分别控制水炮的回转与俯仰，完成定位绝缘子方向的工作；伺服控制动力模块为机械传动模块提供动力与反馈信号，包含2个永磁同步电机、伺服驱动模组以及传感器组，电机为系统运行提供动力源，伺服驱动模组保证绝缘子定位精度，传感器组实时反馈位置信息，起到限位和复位的作用；液压冲洗模块包括液压动力模组和液压传动元件，为水冲洗装置提供高压射流。

现简单介绍机械传动机构的组成与工作流程。如图2所示：俯仰电机通过圆锥齿轮减速器连接角通轴，控制角通轴的回转，通过俯仰角度定位绝缘子高度；回转电机连接圆锥齿轮减速器，减速器输出轴连接小齿轮，以外啮合方式驱动回转支承做回转运动，从而定位绝缘子方向；待定位完成后，启动高压水枪开关，高压水通过水管由下方旋转接头送入，再通过T形旋转接头进入空心角通轴，经炮管后，从炮嘴处射出，冲洗绝缘子。

图2 绝缘子冲洗装置机械结构Fig.2 Mechanical structure of insulator flushing device

在轨道交通清洗工作中，由于绝缘子位置的离散性，导致在连续冲洗多个绝缘子时需要频繁启停设备。在实际工况中，由于伺服系统设定为通用模式，系统各参数设为定值，对于冲洗系统并不是最优方案，每次启停设备时，整个系统将会产生较为明显的振动，在开关高压水枪时，高压水的瞬时反冲力也会冲击整个结构，影响系统稳定性，降低定位精度。在智能装置定位过程中，机械传动系统的质量、惯量、刚度、阻尼等参数均会影响系统的稳定性以及定位的精度。为了合理地设置控制参数，分析伺服驱动控制系统的动态特性，建立动力学模型，通过调节电流环与速度环，在转矩限制下使伺服系统保持稳定性，使其不超过设定的稳态阈值，从而保证水冲洗系统具备良好的动态性能。作者从机械结构模型入手，结合系统控制模型，分析整个系统的响应；再运用MATLAB仿真软件进行仿真模拟，最后在现场实验中验证优化方案。

2 系统数学模型的建立

2.1 机械传动系统动力学模型

由于冲洗装置伺服控制系统的设置参数直接影响结构响应与定位精度，为了更好地确定系统的控制参数，文中首先对此冲洗装置的机械传动系统动力学模型进行分析。智能水冲洗装置的机械传动系统分为两部分，回转模组与俯仰模组，回转模组由炮体、回转支承、齿轮以及圆锥齿轮减速器等组成；俯仰模组由炮杆连接角通轴、T形旋转接头和俯仰减速器等组成。2个电机的角位移作为机械传动系统的输入，炮体的水平转角与炮杆的俯仰角度作为系统的输出。在建模过程中，将机械传动部件的刚度、阻尼、惯量和作用在传动部件上的干扰转矩、圆锥齿轮减速器的传动效率都折算到输出的转动轴上[13]。以回转模组为例，文中建立的机械传动系统动力学模型如图3所示，其中θIN为回转轴的输入端转角，其值为i·θM，i为电机输出轴与回转轴的传动比，θM为电机的输出转角，KL、JL、fL分别为折算到回转轴上的扭转总刚度、转动总惯量和总的黏性阻尼系数。

图3 机械传动系统动力学模型Fig.3 Dynamic model of mechanical transmission system

通过对以上系统的机械传动结构分析，可得其动力学方程组为

(1)

ML(t·i=KL[θIN(t-θL(t]

(2)

θIN(t=i·θM(t

(3)

式中：ML(t)为伺服电机的输出转矩；θL(t)和θM(t)分别为回转轴输出端的等效转角和伺服电机输出转角；Mr(t)为机械传动部件折算到回转轴上的干扰阻力；i为电机输出轴与回转轴之间的传动比。

对式(1)(2)进行拉普拉斯变换，并赋初值0时，得到：

ML(s·i=(JLs2+fLsθL(s+Mr(s

(4)

ML(s·i=KL[i·θM(s-θL(s]

(5)

整理合并式(4)、式(5)后可得：

(6)

若将θM(s)作为系统的输入，θL(s)作为系统的输出，当机械结构的干扰阻尼Mr(s)为0时，θM(s)与θL(s)之间的传递函数为

(7)

以伺服电机输出轴的角位移作为系统的输入，以炮体的回转角位移作为系统的输出，则机械传动系统的系统框图如图4所示。

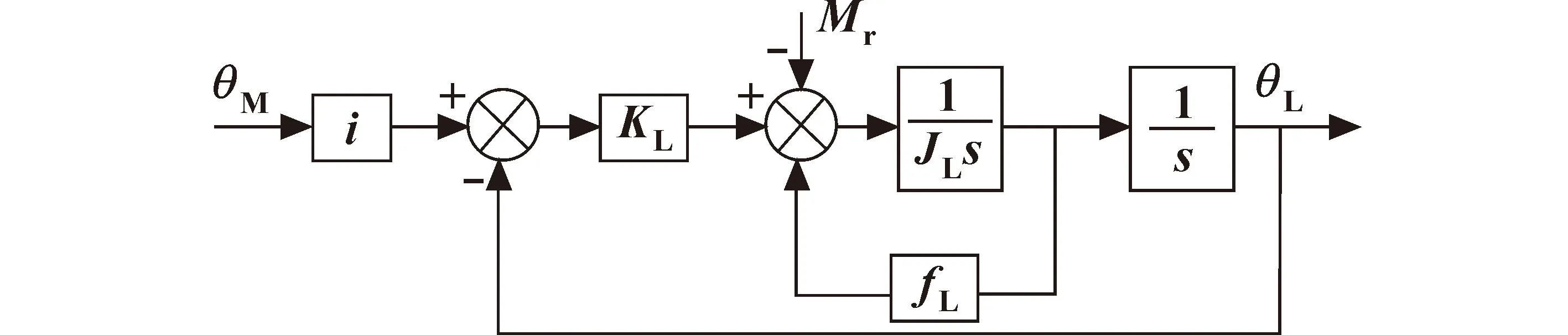
图4 机械传动系统框图Fig.4 Block diagram of mechanical transmission system

基于传动结构的系统传递函数G(s)，将实际结构参数、扭转刚度、转动惯量以及黏性阻尼系数、系统延迟间隙等参数代入后，如表1所示，便可得到此系统的实际传递函数。

表1 俯仰与回转参数Tab.1 Pitch and rotation parameter

根据表1可知，由于传动结构的外部转动惯量已远远超过了电机转子的转动惯量，其数值超过了百倍，而能够正常发挥电机最佳性能的外部转动惯量应在20倍以内。通过分析传递函数，在大惯量结构中，系统对于信号的响应会存在较大振动与延迟，因此，传统的电机控制方法将很难满足对于冲洗精度及稳定性要求较高的绝缘子冲洗装置。在外在条件已经固定的情况下，可以通过改变控制参数，优化电机对于信号的响应，以此来弥补传动结构对于电机的响应延迟与振动带来的影响。表2所示为机械结构中与系统振动有直接关系的影响因素。

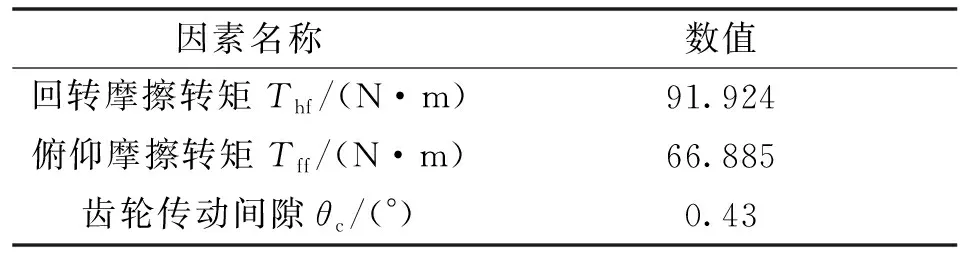
表2 机械结构影响因素Tab.2 Influencing factors of mechanical structure

2.2 伺服驱动系统控制模型

图5 伺服控制系统框图Fig.5 Block diagram of servo control system

修正电流环闭环传递函数，由于伺服系统的速度环带宽远远低于电流环带宽，可简化电流环的闭环传递函数，将高阶项省略[14]，系统电流环传递函数则可表示为

(8)

Tc=Tcf+Tsf

(9)

其中:Tc为电流环的周期时间函数；Tcf为电流环反馈滤波时间常数；Tsf为伺服逆变器的开关时间周期。

于是根据控制结构框图以及电流环闭环传递函数，可以推算出从电机的实际输出速度ωm到速度反馈值ωre的闭环传递函数Gme为

(10)

其中：Kp为系统的比例增益系数；Ki为积分增益系数。

则ωm到Mr的闭环传递函数Gmr可表示为

(11)

2.3 谐振频率分析

根据实际输出速度到速度反馈值的传递函数Gme可以发现，式(10)中的电流环时间常数Tc以及速度反馈时间滤波常数相对很小，当将其化简后，可进一步得到化简后的Gme如下：

(12)

其中：ωn为自然谐振频率；ξ为系统阻尼系数。当系统传递函数Gme简化后，可看作一个标准的二阶响应系统，其中：

(13)

系统谐振频率：

(14)

根据标准二阶系统的频率响应特性，由传递函数可以得出其谐振频率为

(15)

因此，可通过控制系统传递函数以及频率响应特性分析出与电机输出轴振动的有关因素[15]，其中可调节的Kp、Kt、Ki值均会影响谐振频率的大小，对于不同传动结构的系统来说，结构参数Jm也是不同的，因此不仅要分析电气化参数，还要分析负载情况以及结构特性，在实验中才能验证出最优的方案。

3 优化策略与仿真分析

在MATLAB/Simulink仿真软件中建立电气化模型，对系统振动及优化策略进行仿真。以俯仰模组为例，电机参数如表1所示。搭建系统仿真模型如图6所示。

图6 伺服系统电气化仿真模型Fig.6 Servo system electrification simulation model

其中，矢量控制转矩限幅180%，编码器反馈速度滤波时间2 ms，电流环比例系数100，电流环积分系数100，积分时间常数Ti为10 ms，位置环滤波频率fp为40 Hz，速度环滤波频率fv为25 Hz，通过设置不同的参数值，分别在电机刚启动以及加入瞬时负载2个时间点下，观察电机输出轴的响应情况。首先设定初始转速目标值为2 000 r/min，观察系统启动时的响应曲线；然后设定目标值逐步增加至3 000 r/min，观察随着速度变化时系统的振动响应情况。

结果如图7所示，Kp值设定为50，刚启动时，目标转速设定值为2 000 r/min，电机输出轴转矩及转速能够在0.026 s内达到稳定值，但转矩振幅与转速波动却很大，转矩变化频率很高而且Te最大振幅值达到了442.6 N·m，电机输出转速ωn的最大超调量达到了278.2 rad/s。在0.2 s时，开启高压水枪，由于瞬时的反冲力，相当于施加了一个阶跃信号的负载，使系统发生了振动响应，可以看出：在Kp较大时，对于负载的变化，系统的振动响应也较为明显。在伺服控制系统中，较大的速度环增益系数有助于系统的快速响应，能够降低冲洗装置的反应时间。但对于绝缘子智能水冲洗装置，由于实际工况中绝缘子的离散性与随机性，会存在频繁的电机换向启停操作，还存在开关高压射流时的反冲力，较大的Kp不仅会导致驱动系统发生振动，还会放大反冲力对系统的破坏。因此，对于Kp的值应做及时调整，否则会影响冲洗装置的性能。

图7 系统的输出曲线(Kp=50)Fig.7 Output curve of system (Kp=50) : (a)torque Te; (b) speed ωm

通过图7可以观察到：在高速状态下，由于Kp值较大，系统的转矩振动特性与转速振动特性较为明显。但如若将Kp值调小，可以降低振动特性，减小系统冲击，但对于整个系统而言，Kp过低则会降低系统的响应速率，易出现延迟，在绝缘子冲洗过程中，系统的延迟要尽量缩短，否则会大大影响追踪精度。

文中引入了一种时变Kp的控制方法，回转与俯仰过程中的负载速度ωm作为自变量，Kp作为因变量，根据实时速度调节。换言之，就是在速度低的情况下设置较高的速度环增益系数，使系统做出快速响应；在系统速度较高时，降低Kp，从而减缓振动特性。将Kp设置为随速度负相关变化的值，从而在尽量不影响系统响应速度的前提下，提高系统稳定性，降低高速时系统的振动。

Kp=-aωm+b

(16)

根据系统转速要求，在绝缘子智能冲洗过程中，设置a为0.016，b为51.6，则可得到Kp关于ωm的对应曲线，如图8所示。

图8 时变Kp与ωm的关系曲线Fig.8 The relationship curve between Kp and ωm

将其应用于仿真系统中，验证此方法对于系统的振动特性是否具有优化效果。如图9所示，建立自定义模块，将外部转速ωm的值作为PI模块的另一输入端口，并使其作为Kp值的自变量，改变逻辑关系，便可得到优化后的时变PI模块。

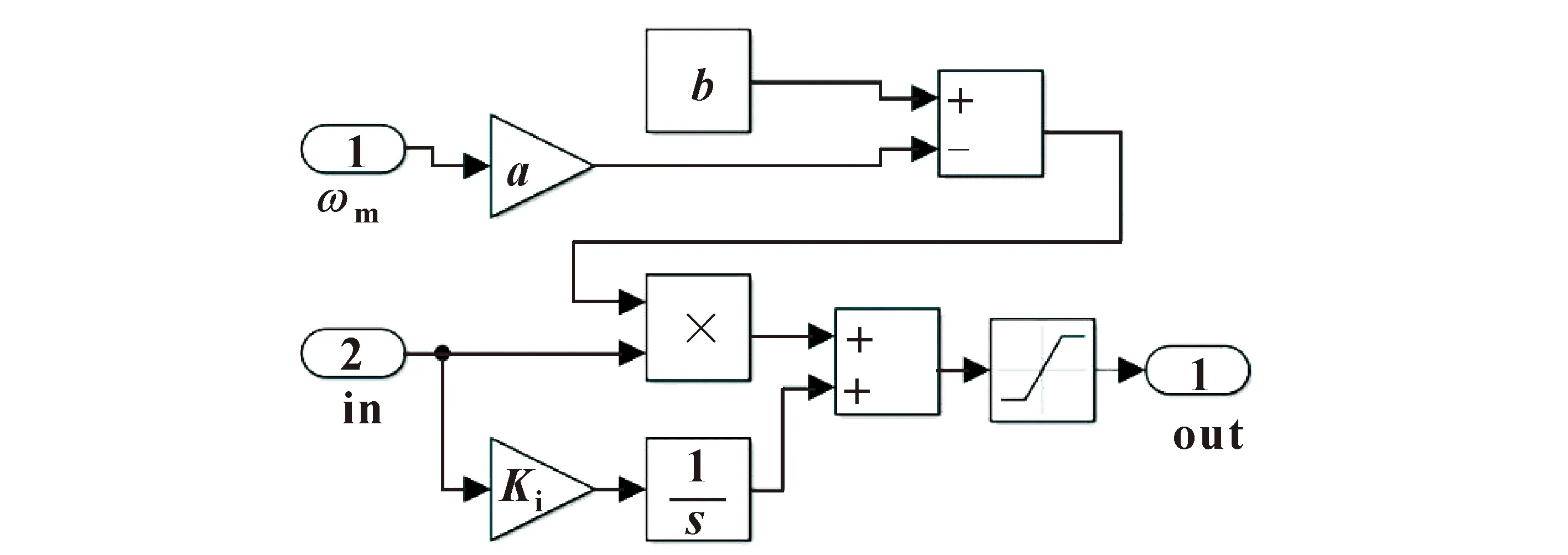
图9 加入速度调节后的PI模块Fig.9 PI module with speed adjustment added

设定相对应的Ki、Ti、fp、fv以及目标转速，便可得到优化后的系统输出曲线前后对比图，如图10所示。

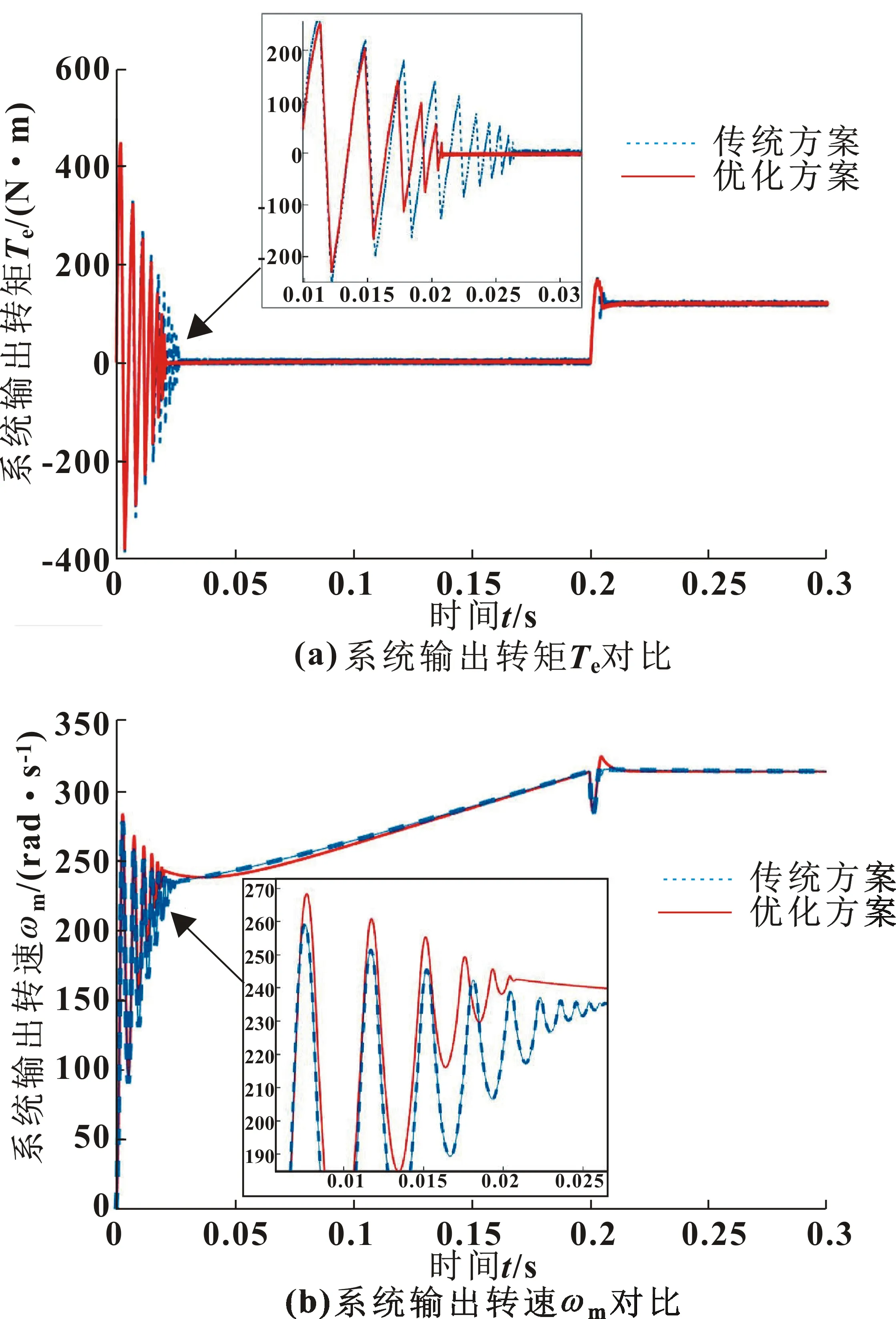
图10 系统响应前后对比曲线

由图10(a)可以看出：使用时变Kp值的优化方案后，系统的转矩响应相较于传统系统，转矩波动得到了有效的抑制，且与传统方案相比，响应时间也有明显缩短，提高了系统19.76 %的响应速度。由图10(b)可知：虽然在负载突变时，优化后的方案对于速度响应没有特别明显的改善，但在系统启动初期，系统的速度响应有较明显的提高，速度波动也有改善。至此，仿真结果表明：文中所使用的时变Kp值的优化方案在仿真实验中能够有效抑制系统由于速度环增益过大而引起的系统振动。

接下来，将在实体机器上通过实验来验证此方案的可行性。

4 实验与验证

图11所示为绝缘子智能水冲洗装置实体，将装置按其功能划分，可分为五部分：追踪定位模块、液压冲洗模块、伺服驱动模块、计算机模块以及限位传感模块。追踪定位模块完成追踪瞄准绝缘子的工作，包含回转模块与俯仰模块，通过伺服电机提供动力分别精确控制回转角度与俯仰角度；液压冲洗模块完成绝缘子冲洗工作，包含高压泵、水箱、换向阀、旋转接头、溢流阀等液压器件，通过运用高压水冲洗射流技术，完成绝缘子的带电水冲洗工作；伺服驱动模块接收计算机发送的绝缘子实时位置信号，通过控制器处理后计算偏转角度，控制回转电机与俯仰电机做出对应转动；计算机模块包括显示器、主机与双目摄像头，运用视觉伺服算法与深度学习网络，对绝缘子进行识别，将位置信号传输给驱动器；限位传感模块包括4个限位传感器以及一个复位传感器，防止炮嘴旋转角度过大而导致内部线路破坏，复位传感器帮助炮嘴复位到初始位置。

图11 绝缘子智能水冲洗装置实体Fig.11 Material object of insulator smartwater-flushing device

电气控制箱如图12(a)所示，包含伺服控制模块、PLC控制器、离心泵控制器、电磁继电器以及传感器模块等。将设计好的硬件板与高速传感器回路封装至控制模块中，加入反馈调节的输入信号，结合PID调节，便可构成伺服控制模块。图12(b)所示为控制炮体回转与俯仰的传动结构，包含两部伺服电机、圆锥齿轮减速器、回转支承、旋转接头以及回转角通轴等构件。

图12 冲洗装置部分关键模块实体

将所有部件安装在平板推车上，如图11所示，在实验阶段，采取移动推车冲洗绝缘子来模拟实际轨道上的实时冲洗情况。

通过示波器，检测电机编码器反馈脉冲数，电机每转动一周，编码器会自动生成一个脉冲，便可通过脉冲数得到实际转速曲线。设定初始目标转速为2 000 r/min，即210 rad/s；待系统响应平稳后，再将目标转速逐步提升至3 000 r/min，即307 rad/s，观测系统攀升曲线；为了与仿真曲线形成对比，实验时在75 ms时间点开启电磁阀，启动水冲洗，此时系统会受到瞬时的反冲力，系统将产生振动响应。

采用控制变量的方法，进行了10次实验，通过10次回转运动的转速输出曲线，取与平均值最接近的曲线，得到了优化前后实际输出转速曲线的对比，如图13所示。可以看出：在优化前，系统初始响应延迟至21.2 ms后振动才相对平稳，而优化后，在17.8 ms后，振动振幅就大致平稳了,响应时间提前了16.1%；但在22～35 ms时间段内，系统转速相较于传统方案数值偏低，经分析，可能是由于Kp值较低，转速回升有所延迟；在75 ms处，由于高压水的瞬时反冲力，系统有明显的振幅变大响应，时变Kp值优化方案相较于传统方案，最大振幅降低了8.6%，波动时间缩短了10.2%，仍具有不小的优化作用。

图13 电机输出转速曲线Fig.13 Motor output speed curves

由图13还能看出，在实际实验中，就算达到目标转速后，系统仍存在转速波动，一直延续到系统关闭。这可能是由于机械结构间存在的传动间隙、回转刚度以及延迟阻尼等现实影响，系统对于振动的响应也相对放大了，导致最后的输出曲线一直呈现出小范围的波动。图14为绝缘子冲洗现场图片。

图14 绝缘子冲洗Fig.14 Insulator flushing

5 结论

通过对绝缘子冲洗原理进行分析，设计了一种绝缘子智能水冲洗装置，并分析了冲洗装置产生振动的原因，列举出了影响因素；根据对具体工况的控制系统的分析，提出了优化的控制方案，以降低电机控制过程对系统振动的影响。

(1)建立了系统仿真控制模型，结果表明：在装置冲洗绝缘子过程中，时变Kp值的优化方案能够有效降低系统的振动响应，缩短了19.76%的响应时间。

(2)将优化方案应用于现场装置，检测其优化性能，通过对实际反馈的转速曲线图进行分析，系统初始响应时间提前了16.1%，在开启高压水枪时的振动振幅降低了8.6%，波动时间也缩短了10.2%，证实了时变速度环增益的优化控制方案的有效性。

后续可对机械结构进行进一步优化，降低结构带来的冲击与延迟；还可对上位机的视觉伺服控制算法进行优化，以适应不同的工况要求，降低振动响应。