PMSM的新型趋近律滑模调速控制器设计*
谭舒丹 马家庆
(贵州大学电气工程学院,贵州 贵阳 550025)
永磁同步电机(permanent magnet synchronous motor, PMSM)具有结构简单、运行可靠、体积小和效率高[1-2]等优良性能,因而被广泛地应用在各种工业场合及生活生产领域中。然而,PMSM在采用数字处理器(DSP)驱动时存在着时滞现象,从而导致驱动器输出电压相位滞后大,电流震荡,系统性能恶化,严重时会使电机失步停机。汪石川[3]等基于PMSM时滞动力学模型展开系统调速鲁棒控制器设计,仿真证明该方案能够有效降低时滞对控制系统稳定性造成的影响,降低电机转速和电流的脉动。朱超威[4]等利用Smith预估器将时滞环节移到闭环之外,在仿真中获得了较好的转速控制效果。
PMSM是一个多变量、强耦合以及非线性的复杂对象,其系统控制一直都是研究热点,因而一些非线性控制方法被不断提出。其中滑模控制(sliding mode control, SMC)理论早已被胡军[5]等成功应用在PMSM控制系统中,并取得了一定的控制效果。SMC不依赖物理模型的精确性,鲁棒性强,因此自提出以来在电机控制领域已经广泛使用[6-9],Xu W[6]等提出一种基于滑模的扩展状态观测器(SMESO),提高了系统的抗扰能力和动态性能。王方凯文[7]等设计了一种基于趋近律的滑模观测器系统,仿真实验证明该方法能够减小转子位置估计误差,提高转子速度估算精度。
基于上述分析,设计了一种SMC速度控制器,提出在实验中进行相图绘制来作为辅助验证。在PMSM的数学模型基础上,引入系统状态变量,提出一种新型幂次趋近律,并使用Lyapunov理论证明该算法的稳定性。仿真和实验结果表明,基于该算法设计的SMC速度控制器和传统SMC速度控制器相比,系统超调小、响应快以及电流脉动小等,增强了系统的稳定性和抗干扰能力,可有效抑制系统抖振。
1 PMSM的数学模型
1.1 时滞现象简单介绍
时滞现象即PMSM在采用数字处理器(DSP)时,当前周期输出的PWM波是上一周期计算得出的,下一周期输出的PWM波是当前周期计算得出的,导致输出电压总是滞后一个周期。驱动器输出电压相位滞后,从而引起电流环震荡、d-q电流脉动变大、系统电流的谐波畸变率(total harmonic distortion ,THD)变大等,使得PMSM调速系统变得不稳定。
1.2 PMSM的数学模型
为便于对PMSM进行研究分析,作如下假设:忽略漏磁通、不考虑磁饱和、不计涡流损耗及磁滞损耗、假设定子绕组三相对称、气隙均匀和忽略转子轴的摩擦[10-11],则在d-q轴坐标系下,PMSM的数学模型如下。

式中:ud、uq表示定子电压的d-q轴分量;id、iq表示定子电流的d-q轴分量;Ld、Lq表示定子电感的d-q轴分量;Rs表示定子电阻;ω表示转子电角速度;β表示黏滞摩擦系数;J表示转动惯量;Ψr表示永磁磁链;TL表示负载转矩;np表示电机极对数。
2 速度环控制器设计
2.1 滑模控制(SMC)
滑模控制也称滑模变结构控制,具有不连续性,即系统结构随时间变化的开关特性,并且系统状态被约束为遵循所需的轨迹,这些轨迹位于状态空间中的合适表面(开关表面或滑动表面)上,对于一般非线性控制系统,则

式中:x为状态变量;u为控制变量。设滑模面函数为s(x),则控制律ui(x)如下。

其中:ui+(x)≠ui-(x)。
SMC控制器的设计就是为了使滑模面s=0以外的任意初始位置在有限时间内趋近和到达滑模面,并沿着预先设定的滑模面运动到平衡点。
2.2 速度控制器设计
趋近律的控制方法是SMC中常用的一种控制策略,设计一个合适的趋近律可以在系统状态离滑模面较近时,速度很小趋近于零,有效减弱抖振;在系统状态离滑模面较远时,趋近速度大,从而加快系统响应。常用的趋近律有等速趋近律、指数趋近律[12]、幂次趋近律等[13]。传统的幂次趋近律如下。
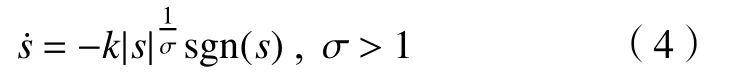
本文基于幂次趋近律,并引入系统状态变量提出一种新型幂次趋近律,其具体形式为

式中:k1、k2、α、β及ε为设计参数,且k1>0、k2>0、α>1、ε>1、β>1和x1为系统状态变量。根据式(1)定义PMSM系统的状态变量为

式中:ω表示给定转速;ω*表示实际转速。对式(6)进行求导可得
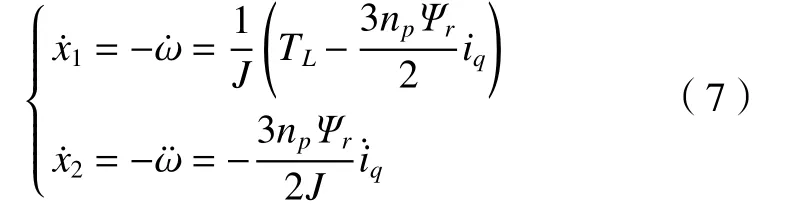

滑模面函数设计为
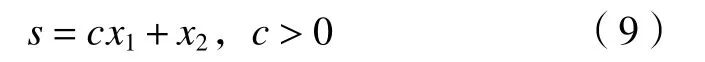
式中:c表示滑模面参数。对式(9)求导,并代入式(8)得:

结合式(5)可以得到提出的新型幂次趋近律SMC速度控制器为

可以看出,控制器式(11)经过了积分器滤波,有利于削弱控制系统中的抖振现象。
2.3 稳定性分析
为了验证本文所设计的滑模速度控制器能否使状态变量在有限时间内到达滑模面,选取Lyapunov函数如下

根据滑模控制理论的基本原理,若要保证所设计的控制器是稳定的,则需满足滑模到达条件

将式(5)代入式(13),可得
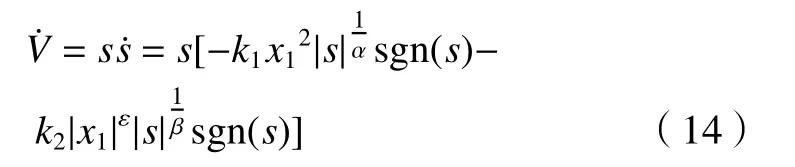
根据设计参数要求,k1、k2、α、ε和β均大于0,可知,该趋近律是满足到达条件的,此时控制系统是趋于稳定状态的。
3 仿真及实验分析
3.1 仿真及结果分析
系统速度环为SMC速度控制器时的系统结构框图如图1 所示。根据结构框图在MATLAB/Simulink中搭建系统的仿真模型,仿真中的电机模型参数与实物平台的电机参数相同。仿真中采用id=0 的控制策略驱动电机,速度控制器中的各个参数为:k1=80、k2=250、α=10、ε=1.6、β=1.23、c=35。

图1 PMSM系统的结构框图
对比实验在相同的仿真环境中进行,并设置相同的指令转速,设置为1 000 r/min,并在0.2 s时突加8 N·m的负载。图2表示PMSM系统的速度环分别为传统SMC速度控制器和本文提出的SMC速度控制器时的速度响应曲线,图3表示d-q轴电流图。

图2 速度响应曲线
由图3可知,本文提出的SMC速度控制器下的系统性能优于传统SMC速度控制器,体现在系统超调小、响应速度快,突加负载后也表现出了更好的抗干扰能力。从图4可较明显看出:提出的SMC速度控制器下加入负载前后的电流脉动均小于传统SMC速度控制器。

图3 d-q轴电流图

图4 PMSM的相电流FFT分析
数值仿真中取载波频率为1 000 Hz和基频为50 Hz时,对C相电流进行FFT分析,选取0.3 s后的一个周期,结果如图4所示。传统SMC速度控制器和提出的SMC速度控制器下的THD分别为19.09%和14.19%,后者的THD较低。
3.2 实验及结果分析
为了进一步验证控制器的有效性,搭建了如图5所示的 PMSM 实验平台, 实验平台的控制芯片选用 TMS320F28335。突加负载是利用 DSP 控制磁粉制动器实现的,实验中所用到的PMSM的具体参数为:定子电阻2.875 Ω,定子电感0.008 5 H,转子转动惯量0.008 kg·m2,永磁磁链0.175 Wb,极对数4。

图5 PMSM系统的实验平台
图6表示突加负载时的速度响应曲线,传统SMC速度控制器和提出的SMC速度控制器下的速度超调分别为90 r/min和25 r/min,响应时间分别为 1 400 ms和 1 000 ms。

图6 速度响应曲线
图7表示d-q轴电流图,为了更直观地了解此处的实验结果,提出从微观角度进行分析,绘制了如图8所示的电流和电机速度的三维相图,从相图中可以看到8b图下的相图轨迹范围明显小于8a图,说明后者较稳定。以上结果表明提出的SMC速度控制器能够有效抑制系统抖振,减小电流脉动,且在突加负载扰动时,速度受到的影响更小,鲁棒性更强。

图7 d-q轴电流图

图8 三维相图
4 结语
针对PMSM矢量控制系统中存在电流脉动大、系统性能差的问题,在系统速度环上,设计了一个积分型的新型幂次趋近律SMC速度控制器。仿真和实验表明,与传统SMC速度控制器比较,突加负载后的系统响应速度快、超调小以及调节时间短,并且削弱了d-q电流脉动。同时,在实验中提出从微观角度分析,绘制电流和电机速度的三维轨迹相图,验证了实验结果和控制器的有效性。

