光学驻波腔实验系统的设计与实现

李林帆，王 菁，李雨阳，周宇奇，牛宇钒，周海涛

(山西大学 物理电子工程学院，山西 太原 030006)

基于法布里-珀罗(Fabry-Perot，F-P)干涉原理[1]的光学驻波腔，可以使注入腔内的相干激光往复传播而发生共振增强. 目前，光学驻波腔已被广泛应用于现代光学的诸多领域，例如在激光光学中应用于激光器的设计[2-4]、激光模式分析和稳频[5-6]，在量子通讯中应用于激光倍频、参量下转换等非经典光场的制备[7-9]和光学精密测量[10]，在腔量子电动力学中应用于光与物质的强耦合作用[11-13]，等等.

根据谐振腔理论可知，腔内光场的本征模由麦克斯韦方程组和腔的边界条件决定. 因此，不同结构和类型的谐振腔，其本征模式也各不相同. 按共振频率区分称为纵模，按传播方向及光强分布区分称为横模. 驻波腔的调节涵盖了光的干涉、腰斑变换和模式匹配等物理知识，是综合程度高、动手能力强、具有较强应用和拓展性的实验，因此，掌握驻波腔的工作原理及调节技术非常重要. 而现有的绝大多数涉及谐振腔的仪器，例如激光器、模清洁器等都是封闭式设计，还没有针对大学本科生或相关技术人员系统学习和训练的开放式驻波腔实验设备. 因而开发适合高年级本科生或低年级研究生学习和训练的光学谐振腔调节系统尤为必要.

本文以对称驻波腔为研究对象，结合F-P干涉仪及模式匹配等理论，以实现驻波腔单模运转为目的，设计了腔长连续可调的开放式光学驻波腔实验系统. 利用该系统不但可以使学生掌握驻波腔调节的全部过程，而且通过调节腔长，学生还可以观察分析腔透射谱随腔长的变化，加深对光学谐振腔工作原理及腔调节技术的认识和理解，为进一步开展有关光学谐振腔的科学研究及应用实践打下坚实的基础.

1 理论基础

2个平行放置的反射镜可组成结构简单的驻波腔，根据反射镜的曲率不同，可分为平面腔、平凹腔和凹面腔. 如果2个球面凹面镜的焦点重合，为共焦腔；如果2个球面凹面镜的球心重合，为共心腔；如果2个球面凹面镜的曲率半径相同，为对称驻波腔. 球面的曲率半径和间距(腔长)是驻波腔的重要参量，能够决定腔内光场的本征模[14]. 本文以2个球面凹面反射镜组成的驻波腔为研究对象，分析驻波腔的工作原理及特点.

1.1 驻波腔纵模共振原理

当光射向驻波腔时，无论是共焦腔还是共心腔，其腔透射和反射都遵从F-P干涉原理，即多光束干涉叠加的结果. 以平面平行腔为例分析驻波腔干涉特点，如图1所示.

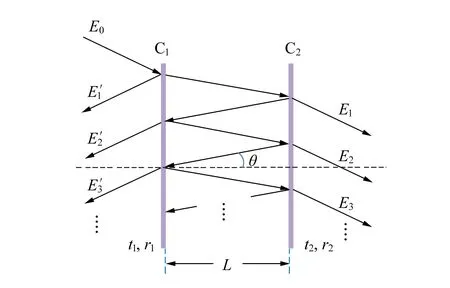
图1 F-P腔干涉示意图

频率为ν0、振幅为E0的相干光入射至由平面镜C1和C2组成的平面平行腔中(腔长为L)，射入腔内的光经过一系列反射后(忽略腔镜的吸收损耗)，利用多光束干涉原理[5]，可推导出腔的归一化透射和反射函数，分别为

(1)

(2)

其中，I0，IT和IR分别为入射光强、腔透射光强和反射光强；r为腔镜总的反射率；δ为相邻2个分振幅之间的相位差.当光波波面垂直于腔光轴时(或在傍轴条件下，即θ≈0)，有

(3)

根据光的干涉原理可知，光在驻波腔内干涉相长的条件是腔长满足入射光半波长的整数倍，即L=qλ0/2，其中λ0=c/ν0为入射光的波长，q为腔的纵模序数(光在腔内沿腔轴向形成的驻波节数).根据式(1)和式(2)，计算r=0.98时，腔的归一化透射强度和反射强度随相位差的变化，如图2所示.可以发现：当δ≠2qπ时，没有谐振产生，入射腔的光能量几乎全部被反射；当δ=2qπ时，入射驻波腔的能量全部被透射.

图2中，腔的相邻2个透(反)射峰(纵模)之间的频率间隔称为光学腔的自由光谱区(Free spectral range,FSR)，其大小为

(4)

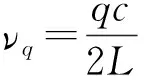
(5)

其中，t为腔镜总的透射率.而腔的自由光谱区与腔模线宽的比值称为腔精细度F，用于度量驻波腔的损耗大小及腔分辨本领的量，表示为

(6)

由式(4)～式(6)可知，当L一定时，腔镜的透射率决定腔的线宽及精细度.图3所示为腔的线宽和精细度随腔总反射率的变化趋势(L=50 mm),可以看出：反射率越大，腔的线宽越窄，其精细度越高，即光分辨本领越大，反映腔的品质因数越高.另外，高精细度的驻波腔在压窄激光线宽的同时也起到滤噪的作用，因此也被称为模清洁器.

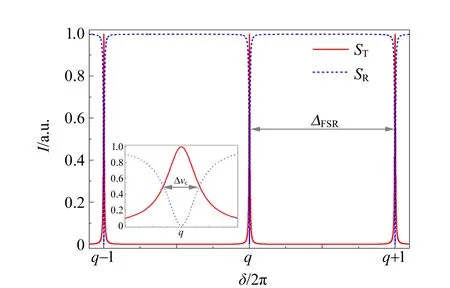
图2 归一化腔透射强度和反射强度随相位差的变化

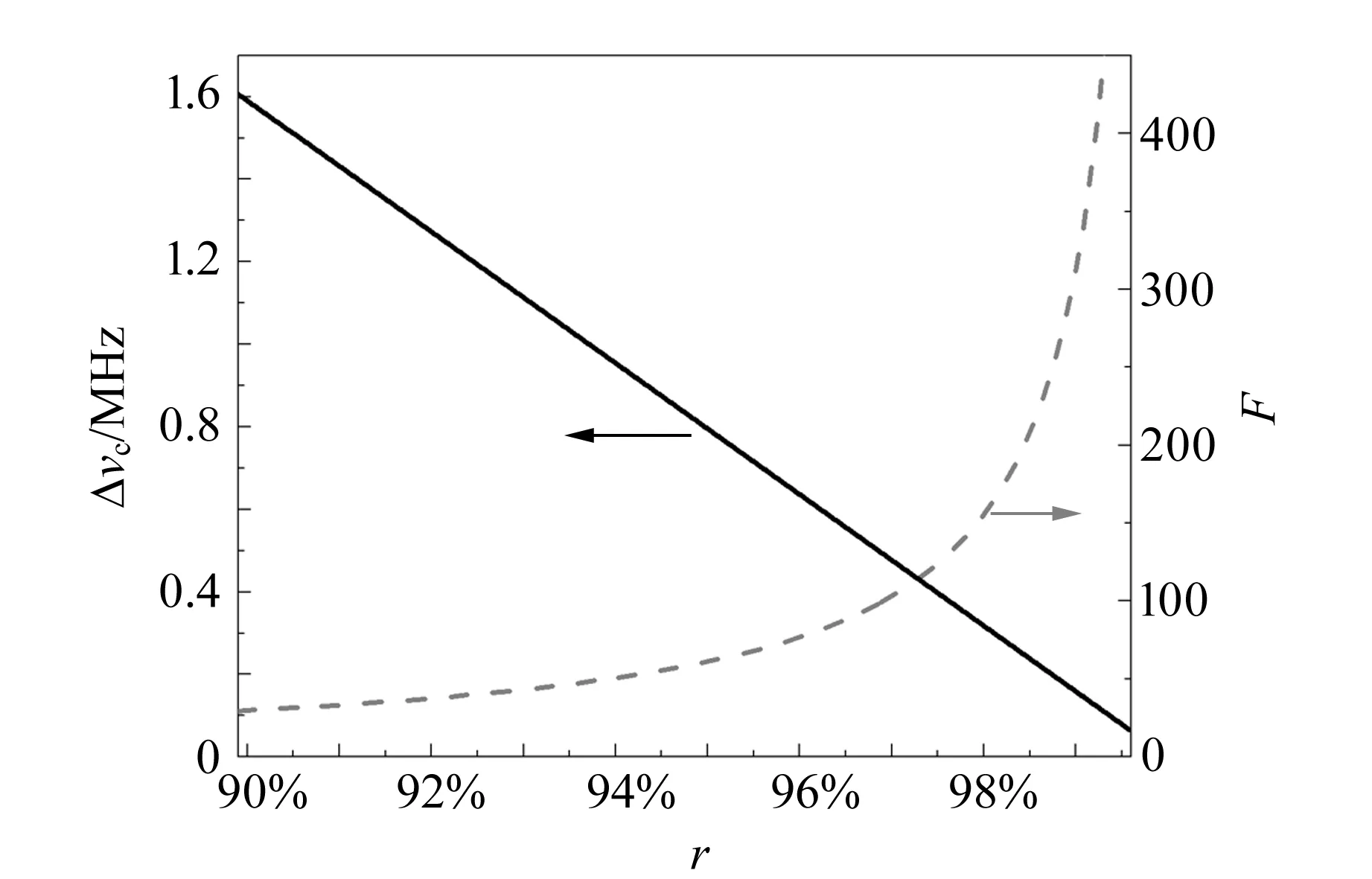
图3 腔的线宽与精细度随腔总反射率的变化

1.2 驻波腔横模模式匹配

垂直于腔轴横截面内的稳定光场分布被称为谐振腔的横模，用TEMmn表示，其中TEM表示纵向电场(z轴)为0的横向电磁波，且m，n≥0称为横模序数，分别表示光场在腔横截面上沿x轴和y轴的节线数.光场满足稳定场分布的条件为在腔内往返传播1次时能实现自再现，所以腔的本征横模也称为自再现模.根据菲涅耳-基尔霍夫衍射积分理论[14]可知，不同形状的球面镜会导致不同的高阶横模模式.例如，方形球面镜产生厄密特-高斯模，圆形球面镜产生拉盖尔-高斯模.但无论哪种球面镜，其基模(m=n=0)均呈现圆形的高斯函数分布，也称作基模高斯光，用TEM00表示.下面重点讨论驻波腔下，基模高斯光束的模式匹配.

如图4所示，假设驻波腔腔镜的光轴沿z轴方向，由于高斯光束在空间呈双曲线型传播，必然存在1个光斑极小值点，称为高斯光束的腰斑位置，其半径(径向方向上由轴心到电场下降到总电场的1/e处的间隔)称为腰斑半径，用w0表示，而其沿轴向传输至任意一点z处的半径(有效束宽)用wz表示.在自由空间下，二者满足

(7)

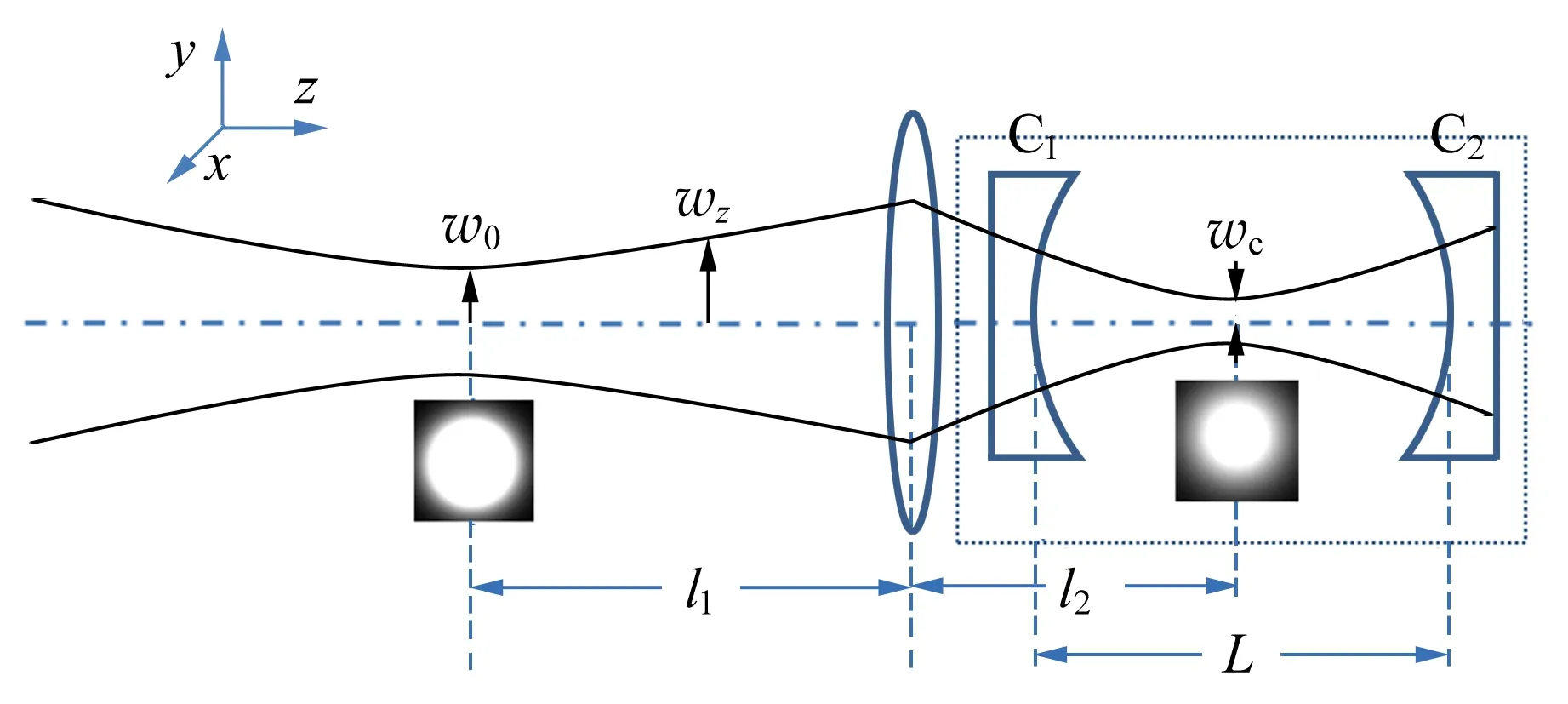
图4 模式匹配光路示意图

当z=0时，wz=w0.对于由2块平凹腔镜C1和C2组成的驻波腔(见图4)，其本征腰斑半径用wc表示.在满足腔的稳定性条件下，wc的大小为

(8)

其中，ρ1和ρ2分别表示C1和C2的曲率半径.当ρ1=ρ2=ρ时，构成对称驻波腔，而腰斑刚好处于腔中心.当腔长L=ρ时，驻波腔为对称共焦腔；当L=2ρ时，则为对称共心腔.实验上通常利用焦距为f的凸透镜(或透镜组)，在有限距离内把自由空间下高斯光束的腰斑w0刚好变换至与驻波腔的本征腰斑wc相同.根据高斯光束在自由空间的传播规律及薄透镜在傍轴条件下的变换矩阵，可推得w0，wc和f三者之间的距离关系为

(9)

(10)

其中，l1和l2分别为透镜距w0和wc的距离.利用式(8)模拟对称驻波腔条件下wc随L的变化趋势，如图5所示.实验中参量设置为:ρ=50 mm，f=150 mm，λ0=852.3 nm.在腔镜曲率半径固定的条件下，当L=ρ时，腔本征腰斑wc最大，且其大小随腔长变化不敏感；而当L逐渐接近2ρ(近共心)时，wc逐渐变小且随腔长变化非常敏感.利用式(9)～式(10)，模拟匹配透镜(f不变)距w0和wc的距离随L的变化趋势，如图6所示.在共焦腔附近时，随L增大，透镜位置变化不明显；当接近近共心腔时，随着L增大，l1显著增加，l2呈减小趋势，但l=l1+l2有增大趋势.

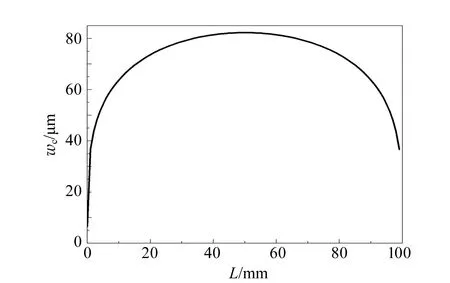
图5 对称驻波腔时wc随L的变化趋势

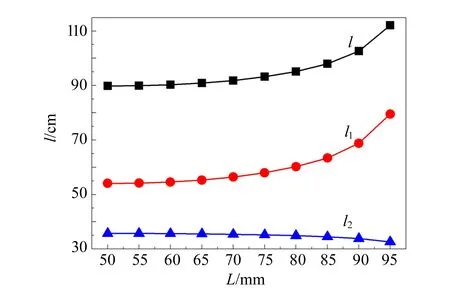
图6 l1,l2和l随L的变化趋势

2 实验过程及结果分析

基于F-P腔干涉理论及腰斑模式匹配方法，设计并制作了腔长可调的驻波腔实验系统. 系统的设计在保证其工作稳定性基础上，以锻炼学生的动手能力为目标. 下面从系统设计、操作步骤和结果分析3个方面进行介绍.

2.1 系统设计

系统的光路部分采用开放式集成化设计，所有光学器件固定于带有等间距螺孔的铝板底座上. 实验装置示意图如图7所示. 实验采用中心波长为852 nm的光栅反馈半导体激光器(最大输出功率为50 mW,自由运转线宽为500 kHz，图中未展示激光器)，激光器输出的光经光纤整形后，通过光纤耦合头FC输出，然后经半波片HWP后被偏振分光棱镜PBS分成2束：反射的光用于测量入射光的腰斑大小及位置；透射的光经4个平面反射镜M2～M5后入射到驻波腔中. 在反射镜M5和驻波腔之间放置可调光阑AD和匹配透镜CL. 经驻波腔透射的光被反射率为10%的分束镜BS分成2束：透射光被光电探测器PD1探测，测量腔透射信号；反射光经衰减片A后进入CCD摄像头，用于监视腔透射信号的光斑模式.

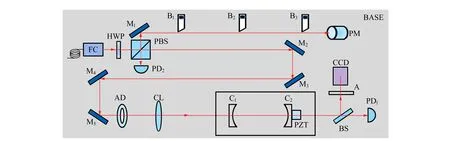
FC.光纤耦合头 M1～M5.45°平面反射镜 B1～B5.刀片挡光器 PM.功率计探头 HWP.半波片 PBS.偏振分光棱镜 AD.可调光阑 CL.平凸透镜(f=150 mm) C1～C2.平凹腔镜(ρ1=ρ2=50 mm) PZT.压电陶瓷BS.分束棱镜 PD1～PD2.光电探测器 A.衰减片 CCD.监视摄像头 BASE.平台底座图7 驻波腔实验系统示意图

驻波腔由2个曲率半径相同的平凹腔镜C1和C2组成，C1作为输入镜，C2作为输出镜并固定在压电陶瓷PZT上，PZT用于扫描和锁定驻波腔的共振频率. 为了实现腔长连续可调，将C1和C2通过3根钢质圆轴相连，并固定于铝制腔底座上，如图8所示. 这样既可以保证腔整体的稳定性，又可以在改变腔长时，保证腔本征腰斑与CL的距离满足匹配条件. 为了避免空气扰动对腔的影响，驻波腔整体罩于有机玻璃外壳中.

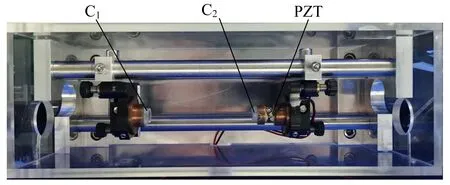
图8 驻波腔实物图

2.2 操作步骤

为实现不同腔长下驻波腔的单横模运转，驻波腔系统的实验过程流程如图9所示.

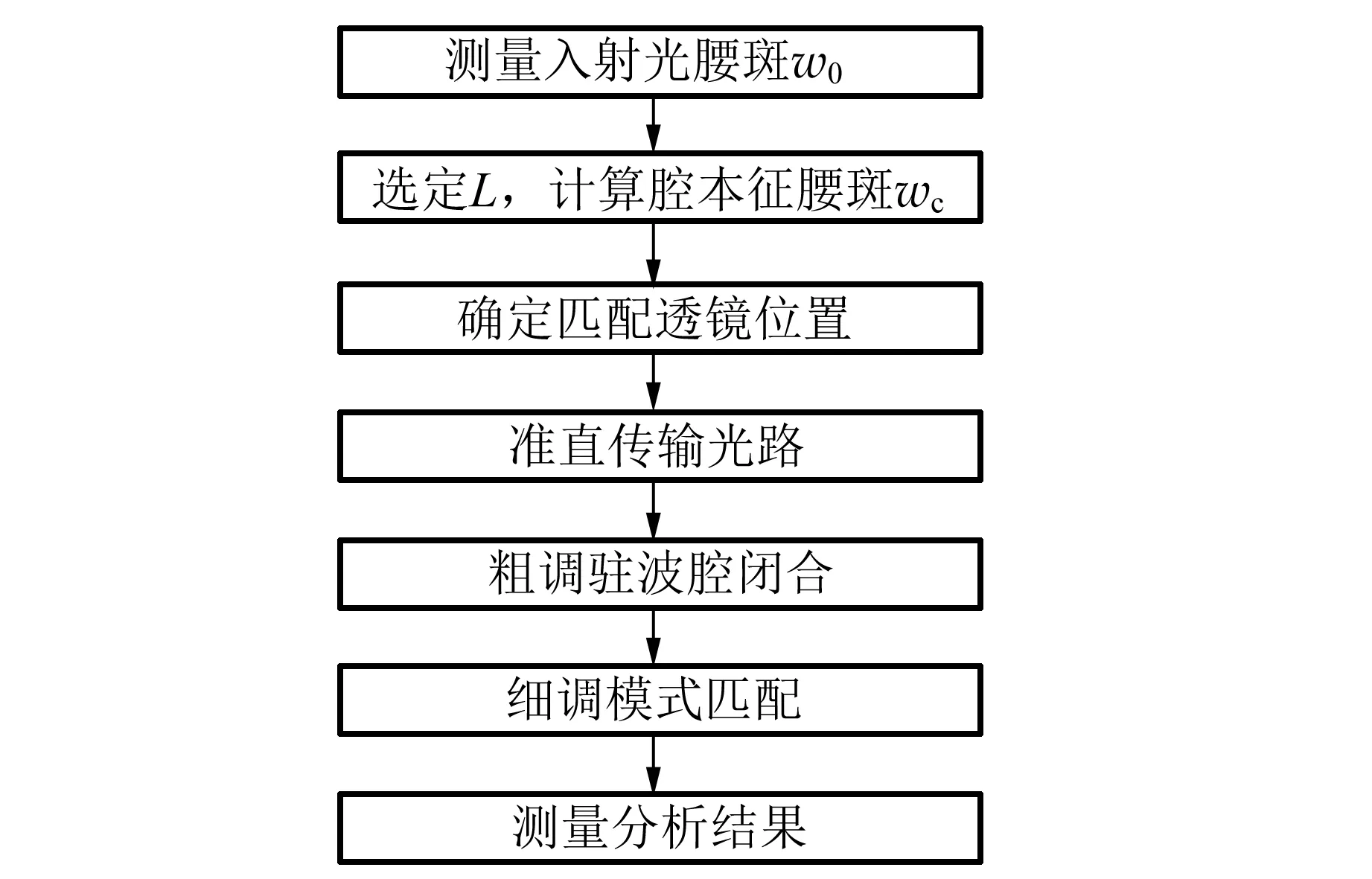
图9 实验过程流程图

系统的操作步骤为：

1)测量入射光的腰斑w0，经FC输出的入射激光可看作圆形基模高斯光束，实验中可利用“刀片法”测量其腰斑w0的大小和位置：以M1的位置为原点，在其反射光线的末端，利用功率计PM测量无任何遮挡时反射光的总功率P0；然后利用刀片挡光器B1～B3等间隔测量3点处的束宽和距M1的距离；再利用式(7)计算求解. 实验中为了减小激光功率不稳定及人为因素，可以采用多次测量求平均值的方法减小误差.

2)选定L，计算驻波腔本征腰斑wc.以L=50 mm为例，由式(9)可知，腔本征腰斑wc大小取决于腔镜的曲率半径、腔长及入射光波长. 本实验系统中，入射光波长λ0=852.3 nm，驻波腔为对称驻波腔，且ρ1=ρ2=ρ=50 mm，因此wc仅与腔长L有关，且其位置刚好处于驻波腔中心.

3)确定匹配透镜位置. 根据实验系统的空间大小及腔镜参量，匹配透镜CL的焦距设置为f=150 mm. 利用式(10)，结合步骤1)和2)计算测得的数据，可以确定透镜分别距离w0和wc的距离l1和l2.

4)准直传输光路. 整个系统的光路要求 “横平竖直”，这主要由4个平面反射镜M2～M5来实现. 根据步骤3)确定CL的位置. CL为平凸透镜，且安装在一维平移台上，使CL可以沿光的传播方向做微小平移. 实验中利用光阑AD辅助调节CL的光轴与入射光重合.

5)粗调驻波腔闭合. 将穿过CL的准直光束作为参考光，将驻波腔底座固定在合适位置，使其满足：a.C1和C2沿圆轨在腔底座上滑动时，入射光始终照射在腔镜的中心；b.腔长L由共焦连续变化至近共心时，腔本征腰斑中心与CL之间的距离l2刚好满足模式匹配条件. 首次安装驻波腔腔镜时，可按照“先输出镜，后输入镜”的顺序放置，并且借助AD调节C1和C2，使其反射的光斑中心恰好处于AD的中心，使得C1和C2的光轴与入射光基本重合.

6)细调模式匹配. 利用信号发生器输出频率约几十Hz的三角波信号，通过带增益放大的高压放大器(型号为YG2013A-500V)放大后加载至C2的PZT上，用于扫描腔长. 此时用示波器监测PD1探测的信号，会看到很多腔透射峰输出，说明模式还没完全匹配，需进一步细调：a.微调C1和C2，使腔透射峰中只有1个主峰的强度明显增加，而其他小峰被显著抑制，直至消失；若微调腔镜至最佳状态后依然还有小模，则可以沿光轴前后微调CL的位置，使小模继续减小至消失，这时腔达到单模运转状态. b.调节高压放大器偏压和增益输出在(300±25) V，保证PZT在三角波扫描1个上升沿(下降沿)范围内，腔透射谱覆盖2个自由光谱区.

7)测量分析结果. 分别利用光电探测器PD1和PD2测量腔的透射信号和反射信号，并记录数据. 利用Origin软件对数据进行处理：分析腔的自由光谱区、腔的线宽及精细度等实验参量，并与理论值进行比较. 若将高压放大器的增益降为0，并调节直流偏压至腔长刚好处于单模共振位置时，通过CCD可观察到腔透射信号呈现的光斑样式是理想的圆形TEM00模.

改变腔长L的大小，重复步骤2)～7)，完成腔的调节和数据测量.

2.3 测量结果及分析

通过步骤1)测得入射光经FC输出的腰斑为w0≈248.3 μm，距M1的距离为z0=24.7 cm. 利用式(9)和式(10)，计算5个腔长下的本征腰斑wc，以及CL分别距w0和wc的距离l1和l2，如表1所示.

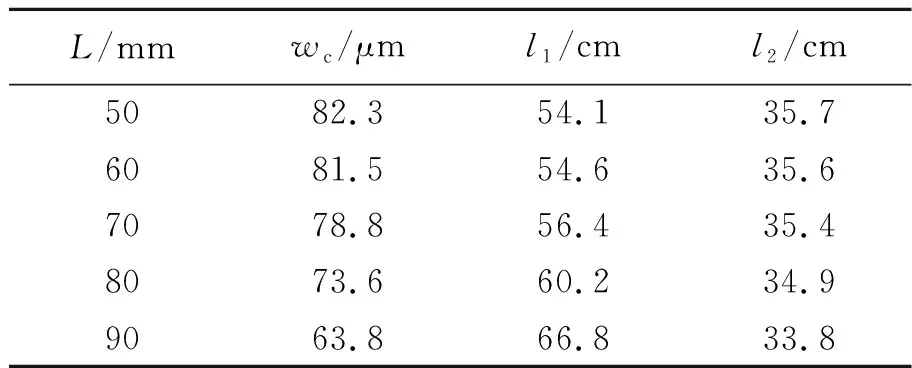
表1 不同腔长对应的测量结果

根据表1数据，首先选择共焦腔(L=50 mm)进行调节，并测量不同状态下的腔透射谱，如图10所示. 固定光频率ν0不变，通过改变腔长L来改变相位差. 图10中的灰色曲线为三角波扫描信号，红色曲线为PD1探测的腔透射信号，蓝色曲线为PD2探测的腔反射信号.

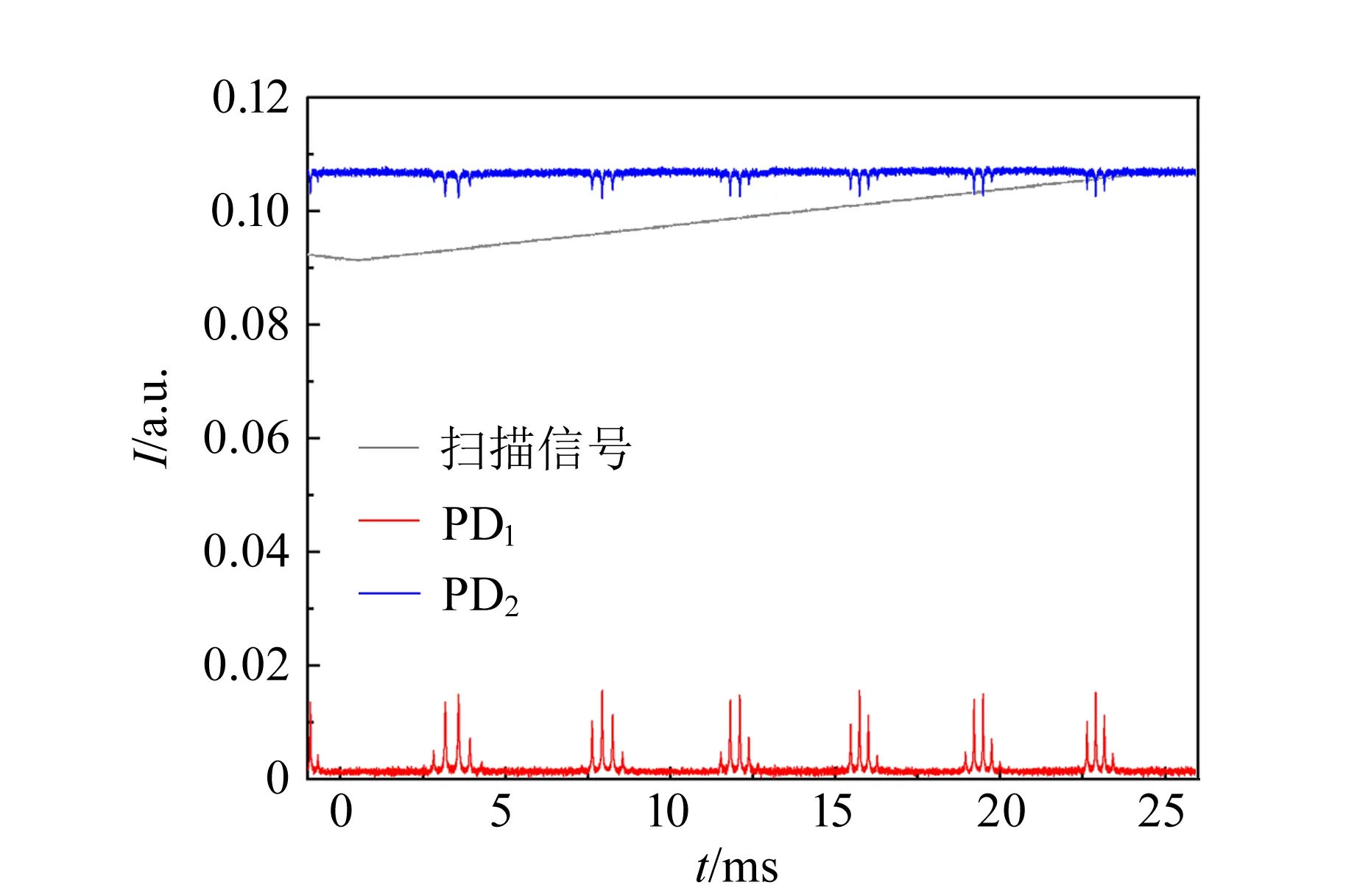
(a)粗调腔闭合

根据步骤5)粗调腔闭合后，腔已有共振峰输出，如图10(a)所示，但此时腔模还未完全匹配，所以激发出很多杂模；在此基础上，通过步骤6)细调模式匹配，最终可实现腔的单模运转，如图10(b)所示. 从图10(b)中蓝色曲线看到，当在单模共振时腔反射峰没达到0，这是由于腔镜参量不满足阻抗匹配所致，即在共振条件下，入射光能量并没有完全耦合至驻波腔中. 根据表1数据，调节并比较了不同腔长下，腔透射谱的变化，如图11(a)所示.

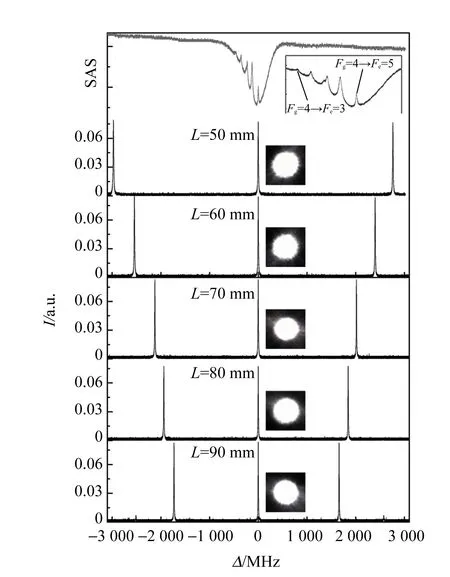
(a)不同腔长下的腔透射谱

与图10不同的是，在每改变1次腔长时，通过固定腔长L和扫描入射光频率ν0来改变相位差. 由于入射光中心频率刚好激发碱金属133Cs原子的D2线跃迁，因此利用饱和吸收光谱(Saturated absorption spectroscopy,SAS)技术来鉴别不同腔长下透射谱的变化[15-16],详细说明可参阅文献[15]. 图11(a)中的灰色曲线显示的是Cs原子基态Fg=4对应的饱和吸收光谱，共有6个饱和吸收峰. 假定原子能级跃迁Fg=4→Fe=5为共振中心，其跃迁频率为ν45，定义入射光的频率失谐为Δ=ν0-ν45，则根据饱和吸收光谱之间的频率间隔，可以将透射光谱的横坐标转化为频率.

从图11(a)可以看出，当L由共焦腔变换至近共心腔时，驻波腔均实现了单横模运转，且ΔFSR随L增加而减小. 图11(b)中黑色方块表示ΔFSR的实验测量值，与式(4)的理论值基本吻合. 腔模线宽Δνc和精细度F随L的变化趋势与理论一致，只是Δνc的实验值整体高于理论值，见图11(c)；而腔精细度F基本保持在237左右，低于理论值314，见图11(d). 误差主要来自腔镜的透射损耗：C1和C2的透射率出厂标定为t1=t2=1.0%±0.2%，λ=800～900 nm，理论计算是按腔总的透射率t=2.0%计算，若只考虑透射损耗，则根据式(6)可推算出该腔镜的实测透射率为t1=t2≈1.4%,λ=852 nm. 当高压放大器增益降为0，且调节PZT偏压和激光器频率ν0至腔共振增强处时，通过CCD监测到腔透射信号的光斑为明显的TEM00模，如图11(a)插图所示，证实了该驻波腔由共焦腔变换至近共心腔过程中，均实现了单横模运转. 另外在不同腔长下，通过连续调谐激光器频率在30 GHz范围内无跳模，驻波腔均能保持稳定的单横模运转输出.

3 结束语

以增强学生实践动手能力及科学创新能力为出发点，设计了适合物理学类及光电信息类专业学生学习和实验训练的开放式光学驻波腔实验系统. 在利用该系统搭建光路、调节驻波腔的实验过程中，学生可以深刻认识F-P腔的物理原理、光学谐振腔模式匹配的基本理论. 通过对驻波腔由共焦腔变换至近共心腔的单模调节及腔透射信号的测量分析，学生还可以进一步熟练掌握光学谐振腔的工作特点. 该系统具有驻波腔模块可以重复拆解安装的优点，能够充分锻炼学生搭建和调节光路的能力. 若结合电光调制器及PID控制器，该系统还可拓展为谐振腔锁频及高阶横模光场制备等光学实验项目，为学生从事有关光学谐振腔方面的科学研究及应用创新提供实践支撑.