利用图像相关性搜寻运动目标

潘祖恒，彭青玉，陆 星,3，陈 筱，李 丹

(1. 暨南大学计算机科学系，广东 广州 510632；2. 暨南大学中法天体测量、动力学与空间科学联合实验室，广东 广州 510632；3. 暨南大学物理学系，广东 广州 510632)

图像减法在探测未知星源、寻找超新星和研究微引力透镜现象方面具有重要意义。文[1]首次在频率域求解卷积核做图像减法，应用图像减法监测微引力透镜现象，并处理了M31星系的数据。最优的图像减法由文[2]提出，这种方法是一种非线性最小二乘拟合过程，即使对于稀疏的视场，并且只拟合一小部分像素时，计算时间也很长。文[3]提出了一种图像减法算法，该算法在图像空间域直接求解卷积核，实质是基于标准线性最小二乘法求解卷积核。这种方法将卷积核分解为多个高斯函数乘以多项式的形式。文[4]使用空间变化卷积核并优化了这种方法的计算策略。文[5]使用文[4]的算法处理了380 GB的OGLE-II bulge微引力透镜数据。

在以上方法中，文[3]提出的方法最为经典。但是，文[3]的方法要求使用者定义高斯基函数的数量、它们相关的sigma值和多项式的阶数，这一系列参数的选择无疑使用户感到困惑，且需要进行大量试验才能获得特定数据集的最优参数[6]。后来，基于文[3]的思想，人们研究了多个类似的图像减法技术。例如，文[6]将卷积核视为离散像素阵列，并直接使用线性最小二乘法求解卷积核的像素值，卷积核的大小成为唯一需要调整的参数。文[7]使用交叉卷积避免对高质量参考图像进行比较的要求。这两种方法都称为去卷积方法，是在文[3]方法的基础上发展起来的。这些方法的缺点是需要调整参数[8]。文[6]方法的计算速度非常依赖于卷积核的大小，随着卷积核增大，计算时间变得难以忍受。此外，这些算法不是局部独立的，处理大图像存在困难，通常需要将图像分成几个较小的部分分别进行处理[5]，而且它们在数值计算上是不稳定的[8]。输入图像或参考图像上的坏像素或饱和像素会对一组在卷积核区域内的像素造成污染。因此，这些方法通常在做图像减法之前需要剔除坏像素和饱和像素，并且应避免使用过大的卷积核[6]。在某种程度上，这些操作增加了图像减法的复杂性，并可能忽略一些有意义的像素。直到文[8]提出了一种基于基本统计原理的算法，该算法颠覆了传统的基于去卷积的图像减法算法的原理，是局部独立且数值稳定的。

本文基于统计原理提出一种较少参数的可替代方法，依据输入图像和参考图像之间的流量分布情况做图像减法。即利用两幅图像同一位置两个小区域之间流量分布的相关性消除两幅图像间相似的部分并保留不相似的部分。基于本文算法，开发了一套以Python语言为接口，C语言为底层实现的图像减法代码。该算法能在极短的时间内搜索运动目标，从而克服人眼搜索运动目标的困难，本文称之为消除相似和保留差异，简称esapd(eliminate similarity and preserve difference)。

1 方 法

为了搜寻运动天体，本文提出了一种基于相关性的图像减法技术，其核心在于使用皮尔逊相关系数求出两幅图像的两个相对应小区域的相关性强弱，当相关性较强时，缩小两幅图像之间的差异；当相关性较弱时，保留两幅图像之间的差异。

如图1，图(c)是图(a)和(b)的差异图，即两幅图像对齐，分别减去自己的背景和归一化后直接相减得到的图像。图(d)是图(a)和(b)的相关图。实验发现，在共同背景区域，相关图的系数主要分布在-0.2到0.2之间(相关图的灰色区域)；在共同非背景区域，相关图的系数主要分布在0.8到1.0之间(相关图的白色区域)；运动目标所在区域的相关性较弱。根据这一发现，缩小相关性较强区域的像素灰度值的差异，保留相关性较弱区域的像素灰度值的差异，即可突出运动目标。运动目标如图(c)的红色圆圈位置，白色区域是图(a)中的运动目标，黑色区域是图(b)中的运动目标。

图1 (a)输入图像；(b)参考图像；(c)差异图；(d)相关图；(e)使用修改过的sigmoid函数后的相关图；(f)阈值图

为获得相关图，我们使用皮尔逊相关系数，其计算公式为

(1)

(2)

其中，i和r分别为在输入图像和参考图像相同位置小区域内的像素灰度值，这两个区域的形状称为p-kernel，它是一个正方形；ui和ur分别为各自小区域内所有像素灰度值的均值；σi和σr分别为各自小区域内所有像素灰度值的标准差；cov为计算协方差；E为计算数学期望；n为p-kernel的像素数量。我们使用(2)式计算皮尔逊相关系数，使用这些小区域内像素的灰度值计算中心像素位置(ic,rc)的皮尔逊相关系数Pic,rc(值为-1到1)。对于边界情况，采用截断处理，即忽略边界以外的像素，减少p-kernel内的像素数量。最后得到一个与原始图像尺寸大小相同的皮尔逊相关系数矩阵P0，简称相关图。一般情况下，皮尔逊相关系数小于0表示负相关，大于0表示正相关。皮尔逊相关系数的绝对值越大，相关性越强，反之越弱。

由于要尽可能地消除两幅图像间相似的部分，并保留不相似的部分，本文使用一个修改过的sigmoid函数修正皮尔逊相关系数值。具体操作方式为

(3)

(4)

(3)式是sigmoid函数，(4)式是修改后的sigmoid函数，其函数图像如图2红色实线，横轴为原始的皮尔逊相关系数值，纵轴为修改后的皮尔逊相关系数值，黑色虚线为没有修改的皮尔逊相关系数的转换关系。皮尔逊相关系数经过修正后的相关图如图1(e)，此时相关图的对比度变得更大，有利于消除两幅图像间流量分布相似的部分，并保留流量分布不相似的部分。需要注意的是，原始的皮尔逊相关系数可能为负值，但其绝对值不会很大，因为对于两幅已经对齐、分别减去自己背景和归一化的图像来说，基本上没有强负相关。使用这种修改过的sigmoid函数可以有效地消除负值的影响。

图2 修改后的sigmoid函数图象Fig.2 Modified sigmoid function

当运动目标与其他天体重叠时，相关性也会出现较强的情况，这不利于保留差异。为了解决这一问题，本文引入差分流量系数。其工作原理为

(5)

(6)

其中，i和r分别为输入图像和参考图像相同位置的小区域内像素的灰度值，这两个区域的形状被称为d-kernel，它也是一个正方形。对于边界处理，采用与求皮尔逊相关系数一样的原则。显然，可以用(5)式得到两个小区域内流量变化的百分比diffic,rc。例如，当一个d-kernel内所有像素灰度值的总和为13，另一个d-kernel内所有像素灰度值的总和为10时，这两个小区域内流量变化的百分比为30%。在(6)式中设置一个阈值T(阈值T的设置详见3.2节)，当diffic,rc≥T时，Fic,rc为0，否则Fic,rc为1。利用这些小区域内像素的灰度值计算其中心像素位置(ic,rc)的差分流量系数Fic,rc。最后，将得到一个与原始图像尺寸大小相同的差分流量系数矩阵F0，简称阈值图，其图像如图1(f)，红色圆圈(即运动目标)内的数值为0。当运动目标重叠区域的流量变化百分比大于等于T时，阈值图可以用来使运动目标在重叠区域的强相关失效，即削弱相关性，以便突出运动天体。

基于以上所得的相关图和阈值图，假设有剔除了坏像素和饱和像素的输入图像I和参考图像R。本文算法的步骤如下：

(1)I和R分别减去自己的背景值，然后归一化得到I0和R0。相关的表达式为

Inb=I-bkg(I) ，

(7)

SI=abs[sum(Inb)] ，

(8)

(9)

Rnb=R-bkg(R) ，

(10)

SR=abs[sum(Rnb)] ，

(11)

(12)

其中，bkg表示求图像的背景值，本文使用文[9]开发的Photutils软件求图像的背景值，其他的方法也可以尝试用来获取图像的背景；下标nb表示去除背景；SI和SR表示归一化的缩放比例；abs表示求绝对值；sum表示求图像所有像素的像素值的总和。去除坏像素和饱和像素是为了确保归一化过程的正确性。

(2)找出I0和R0之间像素灰度值的差异D0。计算公式为

D0=I0-R0.

(13)

(3)消除两幅图像间流量分布相似的部分，并保留流量分布不相似的部分。具体操作为

P0=pearson(I0,R0) ，

(14)

F0=diff(I0,R0) ，

(15)

D1=D0(1-P0F0) ，

(16)

D=D1SI.

(17)

其中，pearson表示计算两幅图像的相关图P0，且P0已经过(4)式修改；diff表示计算两幅图像的阈值图F0。(16)式用来消除两幅图像之间流量分布相似的部分，并保留流量分布不相似的部分，且用阈值图使运动目标在重叠区域的强相关失效。由于在第1步中对I0进行了归一化，需要对它进行恢复，即乘以系数SI得到D(见(17)式)，D就是本文算法得到的加工后的减法图像，简称esapd减法图像。

2 算法性能

为了验证本文算法的性能，我们选择了3份代码与本文算法进行比较。基于Alard方法的代码有ISIS2.2(http://www2.iap.fr/users/alard/package.html)，diapl(https://users.camk.edu.pl/pych/DIAPL/)和HOTPANTS(https://github.com/acbecker/hotpants)，本文选择HOTPANTS作为Alard算法的代表，因为它的接口使用比较方便。OIS(https://github.com/quatrope/ois)中提供了基于Bramich方法的代码，而基于文[8]方法的代码是properimage(https://github.com/quatrope/ProperImage)。本文将这3种算法称为Alard, Bramich和properimage。需要指出的是，esapd, Bramich和Alard都运行在2020 MacBook Pro M1上。由于安装环境的原因，properimage算法运行在台式计算机(Intel(R)核心(TM)i7-10700CPU@2.90 GHz)上，其运行时间约为2020 MacBook Pro M1的1.25倍。在比较4种算法的运行时间时，properimage算法的运行时间乘以0.8，从而可以相对准确地比较4种算法的运行时间。接下来通过试验比较验证本文算法的性能。

2.1 对运动目标的检测

我们测试了2013年2月5日云南天文台丽江2.4 m望远镜拍摄的Apophis图像。由于Apophis的运动速度非常快，我们可以用esapd图像减法技术清楚地看到Apophis的移动情况。本文使用裁剪后的900 × 900的图像进行试验，对于properimage和HOTPANTS，使用默认参数，Bramich使用(21, 21)的卷积核，esapd使用p-kernel大小为7 × 7，d-kernel大小为15 × 15。因为本文的目的是寻找运动目标Apophis，所以设置T为一个较大的值0.5，以确保尽可能地消除较大的残差和去除伪对象。

如图3，esapd算法的减法图像非常干净。在esapd减法图像中，白点是输入图像中的运动目标Apophis，黑点是参考图像中的运动目标Apophis，我们可以很容易地找到运动目标。然而，由算法properimage, Bramich和Alard产生的3幅减法图像并不干净，给寻找运动目标带来困难。通过SAOImageDS9软件[10]观察减法图像的像素值发现，esapd算法可以减得非常干净，而其他方法不能做到这一点，大振幅的残差干扰了对目标Apophis的检测。Bramich和Alard引起的减法伪影使得很难确定一个瞬变源是否真实，根据文[8]的研究，这是由Alard 与Lupton系列方法的不对称性导致的。在本文算法中，我们只需要使用DAOFIND程序[11]搜索运动目标Apophis，而其他3种算法很难用该程序搜索运动目标Apophis。

找到的运动目标Apophis的位置显示在esapd减法图像中的红色圆圈中。值得注意的是，在参考图像的右侧有一个小黑点(绿色圆圈内)，这是由于望远镜的CCD存在缺陷造成的。事实上，黑点的值只比图像背景值9 850小200左右。

图3 2013年2月5日拍摄的Apophis图像的图像减法测试结果。从左到右(顶部)：输入图像、参考图像和esapd减法图像；(底部)properimage减法图像、Bramich减法图像和Alard减法图像

通过人眼观察发现，只有properimage算法才能检测到黑点，因此值得肯定的是，properimage算法在某些方面优于本文算法，特别是在细节检测方面。但总的来说，本文算法具有良好的鲁棒性，而且本文算法运行速度最快。当我们调整卷积核的大小为(31, 31)时，本文算法需要运行191.744 s。

为了验证本文的算法得到的运动目标位置的准确性，我们通过测量减法图像中的目标和输入图像的目标之间位置偏差来进行试验。例如，测量图3中esapd减法图像红色圆圈中的白点位置及其在输入图像中的对应位置，然后计算它们的位置偏差，得到本文算法的位置偏差，同理可得到其他算法的位置偏差。本文使用2013年2月4日云南天文台丽江2.4 m望远镜拍摄的74幅Apophis图像进行试验，它们分别来自5个视场。我们按视场将它们分为5组，然后选取每一组的最后一幅图像作为参考图像，其余的作为输入图像，用输入图像减去参考图像，得到减法图像，使用二维高斯拟合算法[12]测量运动目标Apophis的像素位置。图4显示了本文得到的结果，每种算法都有69个位置偏差。令人惊讶的是，这4种算法得出的位置偏差在均值、标准差和偏移量上基本一致。esapd算法的位置偏差在x轴和y轴都有最小的标准差。在x轴，本文esapd算法得到的均值为0.057 2，标准差为0.181 1；在y轴，esapd算法得到的均值为0.049 8，标准差为0.179 4。可以看出，本文esapd算法得到的目标具有相对稳定的位置。

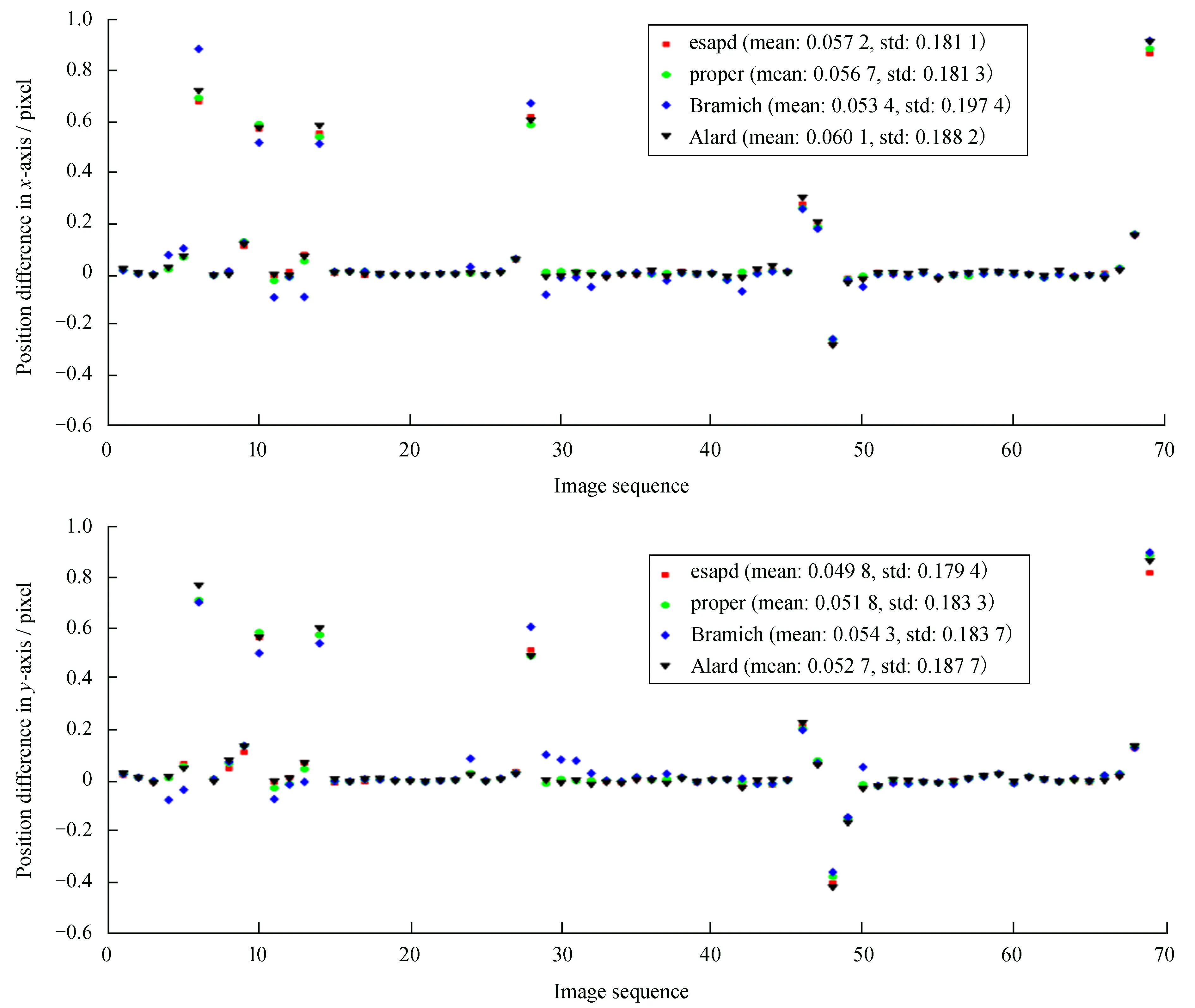
图4 运动目标Apophis在减法图像和输入图像之间的位置偏差,每种算法共有69个位置偏差，平均值和标准差显示在子图的右上角。(a)x轴；(b)y轴

2.2 运行时间对比

我们将从ZTF(Zwicky Transient Facility)下载的M35星团图像的大小裁剪为256 × 256, 512 × 512, ..., 3 072 × 3 072进行计算，然后得到算法的运行时间，单位为s。从图5可以看出，esapd算法的运行时间最快，Bramich算法最慢。当图像过大时，Bramich算法甚至出现无解的情况。

图5 不同尺寸大小的图像在每个算法的运行时间(单位： s)Fig.5 Overview of running time (unit: s) of each algorithm for images of different size

3 解释与讨论

3.1 背景、归一化和对齐

背景去除和归一化是两个重要的步骤，如果没有这两个步骤，本文算法就无法实现。归一化主要用于解决不同曝光时间的问题。需要注意的是，我们的代码并没有提供图像配准算法和背景估计算法。本文使用文[13]开发的图像对齐算法astroalign进行图像的配准工作，使用文[9]开发的Photutils软件进行一维或二维背景估计，其他的图像配准算法和背景估计算法也可以尝试使用。

对齐精度对相关系数具有一定影响。本文使用Photutils生成一幅大小为14 × 14，只含有一颗星且其中心在图像中心的模拟星象图(简称基准图)，然后生成大量类似14 × 14，但包含的星的中心相对于图像中心发生偏移的图像，偏移步长(x和y方向均可偏移)为0.1个像素(简称目标图)。最后利用这些目标图依次与基准图求相关图，并对每个相关图的所有像素求平均值，将此平均值作为偏移后的相关系数。如图6，例如，当x轴和y轴的偏移量为(0, 0)时，相关系数最大值为1；当x轴和y轴的偏移量为(2.5, 2.5)时，相关系数约为0.85。实验发现，偏移量越大，即对齐精度越低，相关系数(未使用sigmoid函数修改)越小；反之，相关系数越大。若把相关系数视为因变量，偏移量视为自变量，因变量与自变量之间类似高斯分布。这一结论说明，对齐精度越高，得到的相关系数越准确。

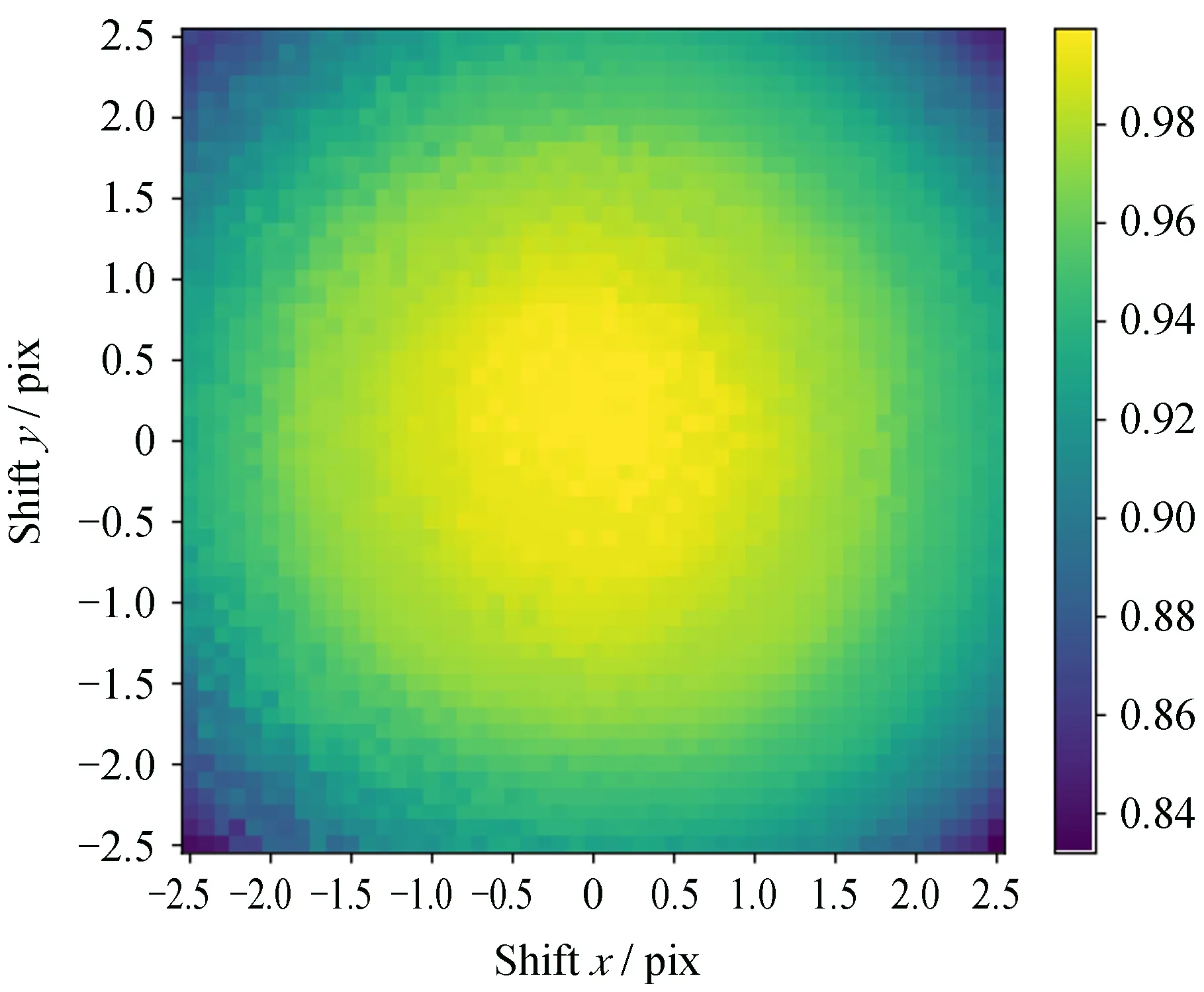
图6 相关系数与偏移量的关系Fig.6 Relationship between correlation coefficient and shift

3.2 kernel与阈值T的设置及算法的适用性

p-kernel的大小与两幅图像的半高全宽(Full Width at Half Maxima, FWHM)之差有关，差越大，p-kernel越大；反之，p-kernel越小。例如，在同一晚上拍摄的图像中，半高全宽相差不大时，可以设置p-kernel为最小值3 × 3。d-kernel与两幅图像的平均半高全宽有关：平均半高全宽越大，d-kernel越大；反之，d-kernel越小。

经实践发现，p-kernel以2～3倍半高全宽之差，d-kernel以2～3倍平均半高全宽来设置效果最佳，即在突出运动目标的前提下减得干净。例如，当半高全宽之差为2.36 pixel时，可以设置p-kernel大小为5 × 5，当平均半高全宽为7.08 pixel时，可以设置d-kernel为15 × 15。当然，此结论仅在处理模拟图像下得出，在处理真实图像时，还需配合阈值T找到合适的参数。

阈值T越小，突出两幅图像差异的能力越强。然而，它并不是越小越好，如果T的值太小，减法图像会出现较大振幅的残差，甚至是伪对象，因为此时相关性容易失效，算法退化为两幅图像直接相减。通常，T值设置为0.1。如果两幅图像差异较大，又想在减得干净的前提下找到运动目标，可以将T设大一点，比如0.5，这里的0.5也可以理解为某一区域的流量变化超过50%且无论相关性强弱如何，两幅图像的差异都会显示出来。

由于本文算法的特殊性，当两幅图像的点扩散函数(Point Spread Function, PSF)差异过大时，例如，一个是圆形的高斯分布点扩散函数，另一个是倾斜的椭圆高斯分布点扩散函数时，本文算法的处理效果并不理想。但是，如果两幅图像都是倾斜角度一样的椭圆高斯分布，本文算法处理效果几乎不受影响。本文算法处理半高全宽相差太大的图像效果也不是很理想，建议使用半高全宽之差在2个像素之内的图像。

3.3 积分图

为了加快皮尔逊相关系数和差分流量系数的计算速度，参考文[14]提出的一种利用积分图快速计算Haar-like特征的方法。从(2)式和(5)式我们可以看到有许多连加运算，本文用这种方法来加快连加运算。积分图的使用不仅提高了皮尔逊相关系数和差分流量系数的计算速度，而且一旦生成积分图，当p-kernel或d-kernel的大小变化时，运行时间不会因此改变，即本文算法的时间复杂度与参数无关。

3.4 噪声估计

(18)

该公式仅适用于Fic,rc=0或相关强度很弱(皮尔逊相关系数的值小于0.2)的情况。

4 总结与展望

本文提出了一种可供选择的图像减法算法esapd，期望将其应用于搜索运动目标。该算法旨在利用相关性消除两幅图像间具有相似流量分布的部分，保留具有不同流量分布的部分。试验表明，该算法可以在短时间内找出两幅图像之间的差异，并搜索运动目标。同时，该算法存在一些不足，如果两幅图像的点扩散函数分布差异过大，本文算法处理的效果有待提高，因此，后续工作将结合使用点扩散函数来进一步研究天文图像减法技术。

致谢：感谢云南天文台丽江观测站2.4 m望远镜工作人员的支持，感谢郭碧峰在论文写作过程中给予的帮助。