基于改进Shapley值的全过程工程咨询联合体收益分配研究

桑培东 秦丽君

(山东建筑大学管理工程学院，山东 济南 250101)

0 引言

在“供给侧改革”和“一带一路”倡议的大背景下，传统的工程咨询模式存在咨询团队整体水平不高、低价竞争明显等诸多问题，阻碍了建筑业的绿色健康发展。2017年2月，国务院办公厅印发《关于促进建筑业持续健康发展的意见》(国办发〔2017〕19号)，提出要培育一批具有国际水平的全过程工程咨询企业[1]。目前，我国能够提供全过程工程咨询服务的独立咨询企业较少，大部分咨询企业只有以联合体的方式发挥各方优势，才能高质量、低成本地完成全过程工程咨询项目。作为追求收益最大化的理性人，联合体中的任何一方对分配方式不满都会影响服务质量。因此，公平合理地进行收益分配成为全过程工程咨询项目联合体成员合作共赢的关键所在。

我国全过程工程咨询模式起步较晚，目前大部分研究主要集中于全工程工程咨询发展困境分析及建议、组织模式、服务模式等方面，针对收益分配的研究较少。崔淑梅等[2]基于对资源投入、风险分担、合同执行度、创新能力4种因素的综合分析，对传统的Shapley值进行改进，使得全过程工程咨询联合体收益分配更加公平合理，为今后的相关研究奠定了坚实基础。

Shapley值法主要应用于多人合作博弈分析和求和问题[3]。在实际项目中，由于联合体各成员的风险分担能力和风险偏好不同，联合体各方承担的风险存在一定差异。因此，运用云重心法确定联合体各成员的风险因子，对传统的Shapley值法进行改进，建立全过程工程咨询联合体收益分配模型，能够使分配方案更加公平，从而激发联合体成员参与项目的热情，促进全过程工程咨询模式的推广。

1 全过程工程咨询联合体收益分配模型构建

1.1 识别收益分配影响因素

在经济活动中，联合体中的各成员被视为理性经济人，其行为以利益最大化为基础，其活动主要是对所面临的风险进行评估[4]。根据全过程工程咨询风险因素研究成果，将全过程工程咨询联合体成员收益分配影响因素分为市场风险、政治及自然风险、技术风险、运营风险和管理风险。

1.2 基于Shapley值法的收益分配模型

将全过程工程咨询联合体收益分配问题看作各成员之间的合作博弈问题，假设联合体中有n个成员，则联合体成员合集N={1，2，…，n}。在本研究中，N={1，2，3}表示全过程工程咨询联合体项目中设计单位A、监理单位B、咨询单位C的集合。

用函数(v)表示在协作过程中联合体成员获得的最大收益；用v(S)表示联合体成员之间不同合作方式而产生的不同收益。v(S)满足以下约束条件，即

V(∅)=0，∅为空集

(1)

V(S1∪S2)≥v(S1)+v(S2) ，S1∩S2=0

(2)

式(1)表示当联合体各方均不参与此项目时，收益值为0。式(2)表示当联合体成立后，整体产生的收益应不小于各成员独立行动时获得的收益之和，即Shapley值的超加性条件[5]。因此，合作是全过程工程咨询联合体各方实现自身收益最大化的最优选择。

φi(v)表示企业i从全过程工程咨询项目联合体收益分配方案中分配到的Shapley值，当φi(v)同时满足可加性、对称性和有效性三个条件时，该收益分配方案有且仅有一个Shapley值，即

φi(v)=∑S⊂Nw(|s|)[v(S)-v(S-{i})] (i=1,2,…,n)

(3)

(4)

式中，v(S-{i})表示去掉成员i后子集S的收益；w(|s|)表示加权因子；|s|表示子集S中的元素个数。

Shapley值体现了联合体成员在联盟中的贡献，贡献越多，收益分配越多；反之，亦然。该方法符合按贡献分配的原则，具有一定的合理性。

1.3 基于云重心法改进Shapley值的收益分配模型

云重心法主要解决定性概念与定量数值相互转换过程中的模糊问题，用期望值(Ex)、熵(En)、超熵(He)表示。公式为G=L×H，其中，L为云重心的位置，即期望值Ex；H为云重心的高度。随着L、H的不断变化，G也会不断变化。当L相同时，可通过H判断各云的重要程度。计算过程如下。

1.3.1 构建综合评价指标体系

设指标体系中指标集合为y={y1,y2,…,y5}，其中，yi表示所有评价指标中的第i个指标，即全过程工程咨询联合体项目中影响收益分配的第i个指标。

1.3.2 建立指标评语集并计算权重

通过专家访谈法确定评价指标体系中各指标权重，并将各指标权重集合记为ω={ω1,ω2,…,ω5}。通过建立三级评语集P3={一等，二等，三等}，对各指标权重进行定性评价，用云模型进行表达。指标权重评语集及云表达模型见表1[6]。

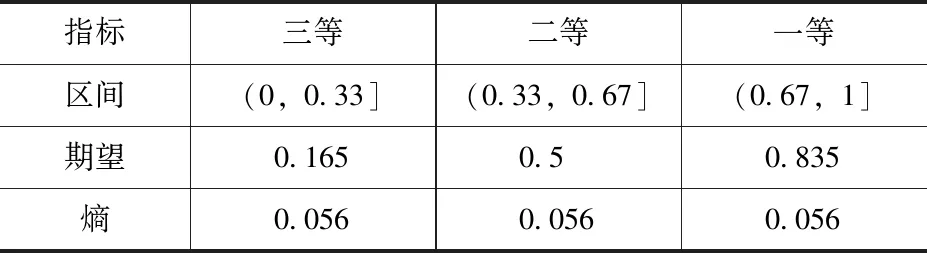
表1 指标权重评语集及云表达模型

针对评价对象设计评语集，采用双边评语表达。公式如下

(5)

式中，Cmax和Cmin分别表示评语取值的上限和下限；Exi和Eni分别表示第i个指标对云模型的期望值和熵值；He表示云模型的超熵，用常数k表示。

假设邀请m名专家参与项目风险影响因素评估，将定量指标的数值转化为云模型，公式如下

(6)

将各指标对应的期望值Exi进行归一化处理，得到各指标权重ωi，表示各指标的相对重要程度。

1.3.3 建立优化收益分配影响因素评语集及云模型

全过程工程咨询联合体优化收益影响因素的综合评价结果用5级评语集P5={极小，小，一般，大，极大}表示，将5个评语放置于连续数值区间[0,1]的子区域。优化收益影响因素评语集表达及云模型见表2[6]。

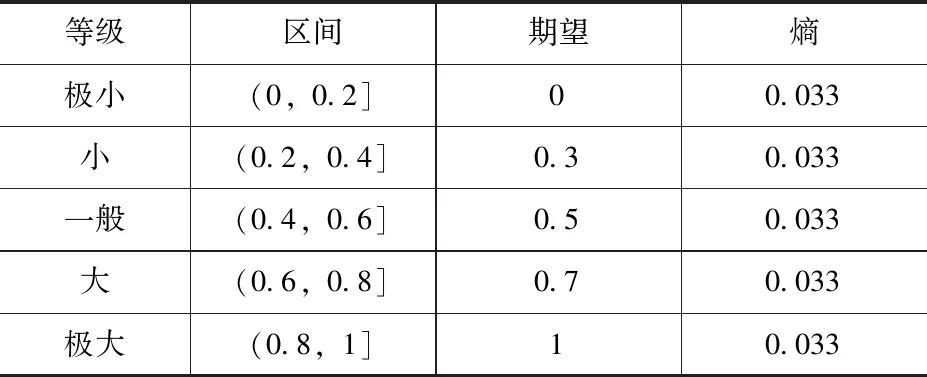
表2 优化收益影响因素评语集表达及云模型

通过专家访谈法收集访谈结果数据，整理后得到综合决策矩阵G={G1,G2,…,Gn}，进而根据式(5)转换成云模型。

1.3.4 计算加权偏离度

由上文可知，n维综合云的云重心可以用式(7)表示，理想状态下的云重心用式(8)表示。但是，在实际情况中，n维综合云重心会偏离理想状态，偏差可用加权偏离度Ω进行衡量。公式如下

(7)

(8)

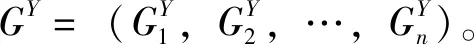
(9)

(10)

1.3.5 计算最终收益值

将各加权偏离度Ω进行归一化处理，得到联合体各成员的权重值；联合体各成员的收益修正值Δφi(v)可用式(11)求得。即

(11)

全过程工程咨询联合体成员在考虑各自风险因素的条件下，最终的收益分配可用式(12)表示，即

φi(v)*=φi(v)+Δφi(v)

(12)

基于上述分析发现，利用云重心法修正Shapley值，既能考虑到全过程工程咨询联合体成员各自的风险因素对收益分配的影响，又能克服定性指标量化转化时存在的模糊性、随机性等问题，使收益分配更为合理，从而有效调动联合体各成员的参与积极性。

2 数值模拟

假设由设计单位A、监理单位B和咨询单位C三家企业组成联合体，记为N={ 1，2，3}。该联合体共同为某大型项目提供全过程供咨询服务。若A独立完成此项目，可获得收益1300万元；若B独立完成，可获得收益1100万元；若C独立完成，可获得收益750万元；若A和B合作完成此项目，可获得收益2900万元；若A和C合作，可获得收益2400万元；若B和C合作，可获得收益2100万元；若A、B、C合作，可获得收益4600万元，即全过程工程咨询合同总额为4600万元。

2.1 基于Shapley值法的初始收益分配值求解

由上述分析可知，三者合作时的收益最大，为4600万元。根据式(3)和式(4)，计算各单位的初始收益分配值。以设计单位A为例，其在不同合作方式下的收益分配值见表3。

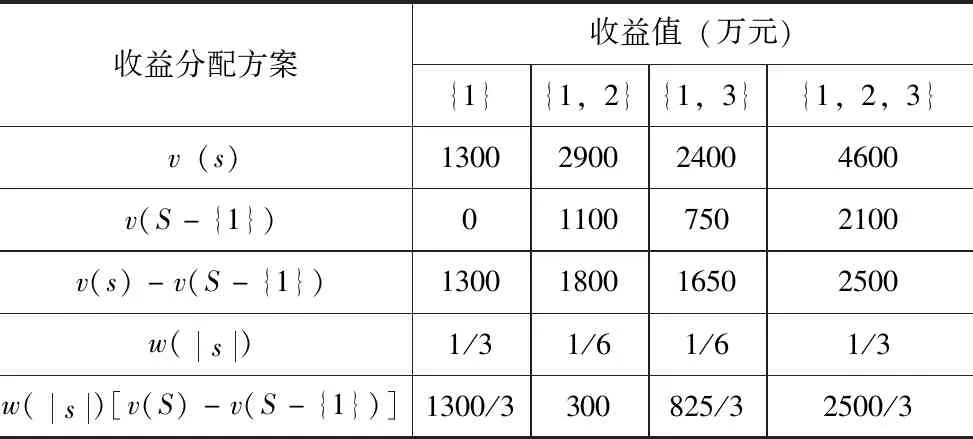
表3 联合体成员A在不同合作方式下的收益分配值

经计算可得，φ1(v)=1300/3+300+825/3+2500/3=1842(万元)。同理，可得φ2(v)=1592(万元)，φ3(v)=1167(万元)。

以上分析表明，在全过程工程咨询项目中，各联合体成员的收益均比他们单独参与此项目时的收益大，有利于提高各参与单位的积极性。

2.2 云重心法改进Shapley值模型求解

2.2.1 建立指标评语集并计算相应权重

邀请6名全过程工程咨询领域专家对5个风险指标进行评判，根据专家评判的原始数据(表4)，计算各风险权重值。

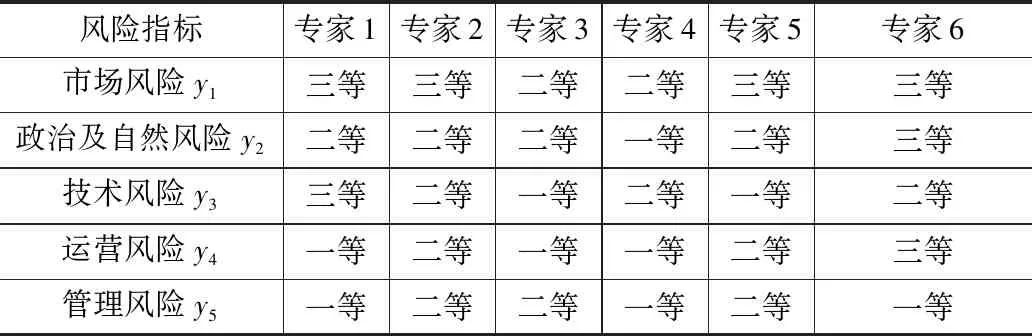
表4 各风险指标评判结果

将表4中的数据进行转换，构建云模型，公式如下

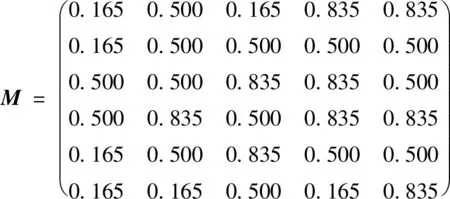
根据式(5)和式(6)计算得到各影响因素对应的期望值、熵及权重值，结果见表5。

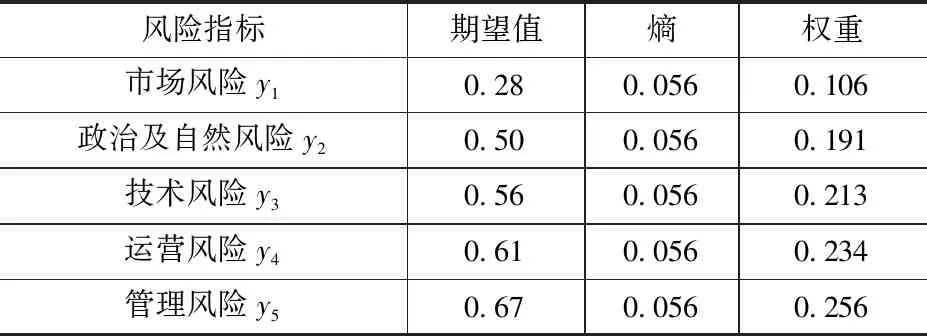
表5 各风险指标期望值、熵及权重值

2.2.2 统计各因素状态值并用云模型表示

根据5级评语集，邀请6名专家对风险指标进行打分。以设计单位A为例，各因素对设计单位A的优化收益分配影响程度见表6。

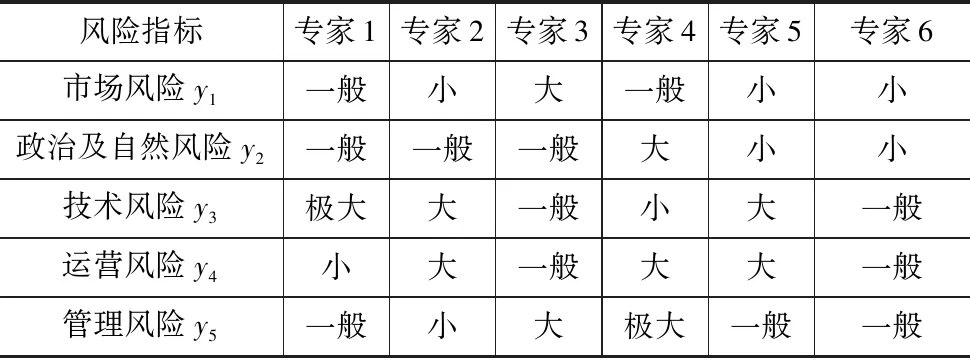
表6 各因素对设计单位A的优化收益分配影响程度

将设计企业A的状态值转换为云模型表达，得到综合决策矩阵，如下

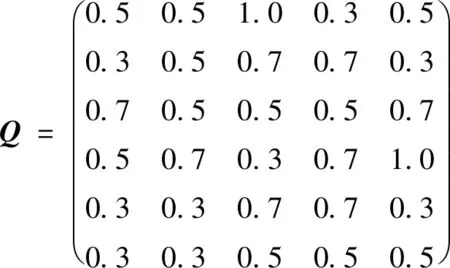
根据式(5)和式(6)，得到设计单位A的各风险指标期望值、熵及权重值，见表7。

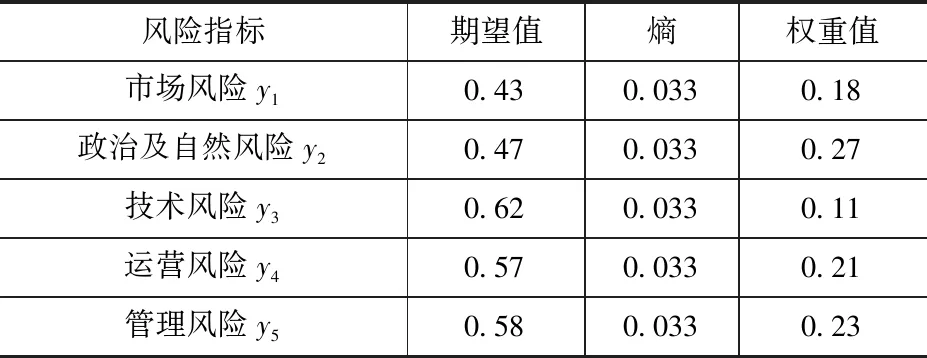
表7 设计单位A的各风险指标期望值、熵及权重值

2.2.3 计算综合云模型的加权偏离度

根据上文公式，得到设计单位A的5维综合云的云重心为G1=L×H=(0.046,0.089,0.131,0.133,0.149)

由式(10)可得设计单位A的加权偏离度为

同理，可求得监理单位B、咨询单位C的加权偏离度分别为Ω2=0.320,Ω3=0.296。

2.2.4 修正初始Shapley值

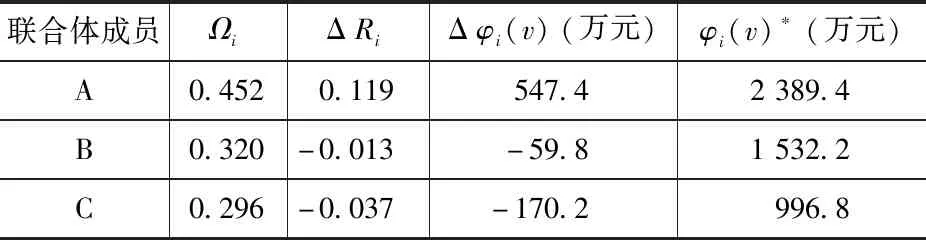
表8 根据云重心法修正Shapley值的收益分配值

2.3 综合收益分配结果分析

将初始和改进后的联合体收益分配值进行汇总，结果见表9。将三种收益分配结果用柱状图表示，如图1所示。

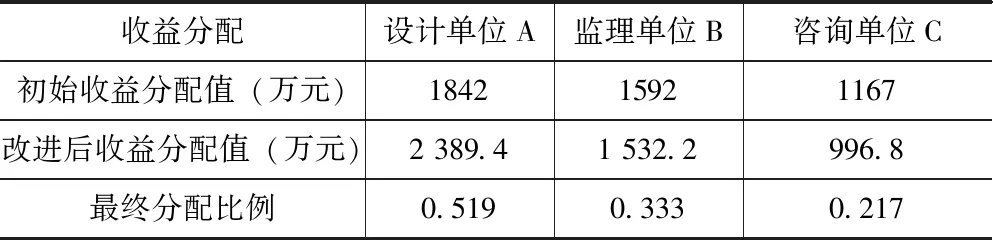
表9 联合体收益分配结果

(1)在改进后的收益分配方案中，三方组成的联合体收益大于各方单独完成此项目的收益，证明全过程工程咨询项目组建联合体的重要性和必要性。

(2)在初始分配方案中，设计单位A、监理单位B和咨询单位C的收益分配值分别为1842万元、1592万元和1167万元；在改进后的收益分配方案中，三方的收益分配值分别为2 389.4万元、1 532.2万元、996.8万元；三方收益分配比例约为5 ∶3 ∶2。在考虑了风险因素的条件下，设计单位的收益有所增加，而监理单位和咨询单位的收益有所减少，这样的分配结果更为合理，更容易被联合体成员所接受，更好地实现了全过程工程咨询项目的增值。

3 结语

建立全过程工程咨询联合体是未来建筑工程咨询行业改革发展的新趋势。本文将风险因子引入传统的Shapley值法，采用云重心法对其进行改进，得到最终收益分配模型，并通过算例验证该模型的可行性。研究结果显示：联合体各成员修正后的收益增长分别为547.4万元、-59.8万元、-170.2万元。这是由于设计单位作为全过程工程咨询项目的牵头方，承担的风险大，获得的收益高，符合“高风险、高回报”的原则。因此，考虑风险因素的收益分配模型既能保证联合体各方收益分配的公平性和合理性，又能调动联合体各方参与项目的积极性，具有积极的激励作用。