8m中国巨型太阳望远镜偏振光学设计*

付玉 袁沭 金振宇 刘忠

(1 中国科学院云南天文台 昆明 650011)

(2 中国科学院大学 北京 100049)

1 引言

中国巨型太阳望远镜(Chinese Giant Solar Telescope,CGST),是中国下一代大口径地基太阳望远镜[1-3].8 m环形太阳望远镜是该计划的主要技术方案[4-5].其重要的科学目标是观测太阳大气中最细微的磁流体动力学结构.这要求望远镜同时具备高精度与高空间分辨的磁场观测能力.在光学波段,太阳大气中的磁场表现为谱线的偏振轮廓,即Zeeman效应或Hanle效应.根据磁场测量精度的要求,CGST的偏振测量精度要求优于2×10-4,即由望远镜测得的相对Stokes参数的不确定度不能超过该值.

仪器偏振是大型太阳望远镜偏振测量的主要误差源,它主要由折轴光路引起,是望远镜光学结构、观测波长以及镜面镀膜材料的函数.偏振定标能够降低仪器偏振对测量精度的影响[6-7],一般情况下,其绝对精度能达到望远镜固有偏振的1%[8].云南抚仙湖一米新真空望远镜(New Vacuum Solar Telescope,NVST)的折轴光学系统具有很强的仪器偏振[9].通过使用基于望远镜偏振模型的定标方法,我们将仪器偏振的影响控制到了5×10-3以下[10-12].要进一步提高望远镜的偏振测量精度就要在设计之初考虑系统的偏振优化,以降低其固有仪器偏振的程度.在折轴系统中采用偏振补偿设计是降低望远镜仪器偏振的有效手段[13-15].例如,4 m European Solar Telescope (EST)太阳望远镜使用了多组交叉折轴镜(Crossed folding mirrors)解决了系统偏振特性随传导光路(transfer optics)指向运动的矛盾[16-17].CGST的折轴光路将采用独特的偏振补偿方案,以保证其在任意指向下都具有极低的仪器偏振.但由于在各补偿镜上入射角不一致、入射面不正交,偏振补偿设计并不能完全消除轴外光线的偏振效应.而基于轴上光线的偏振模拟方法不能分析轴外光线的仪器偏振问题.在4 m Daniel K.Inouye Solar Telescope (DKIST)太阳望远镜的设计与建造过程中,偏振光线追迹方法被用于模拟分析各种仪器偏振效应[18-25].在CGST的设计中,我们使用自主开发的偏振光线追迹程序研究了拼接主镜的综合仪器偏振[26]以及库德焦点的偏振成像特性[27].该程序还被用于分析39 m欧洲极大望远镜(European-Extremely Large Telescope,E-ELT)的偏振特性[28-30].

本文将给出CGST的偏振光学设计,并利用偏振光线追迹方法分析仪器偏振的孔径效应、视场效应及视场效应随望远镜运动和观测波长的变化.在第2节,我们首先详细定义CGST偏振光学的设计要求; 然后,在第3节描述CGST的光学结构,及其偏振补偿的基本原理; 研究中使用的光线追迹算法将在第4节详细介绍; 偏振模拟的结果将在第5节给出; 最后是结论.

2 CGST的偏振光学设计要求

太阳磁场的偏振信号由Stokes向量Sin=(I,Q,U,V)T描述,其中I表示光强,Q代表垂直与水平偏振分量,U代表45°和135°偏振分量,V代表左旋和右旋圆偏振分量,T表示矩阵转置.望远镜对入射偏振信号的变换可表示为Sout=MSin,其中M为望远镜的缪勒矩阵.缪勒矩阵的数学形式如下所示

根据不同的物理意义,缪勒矩阵各元素可以分成以下3类:

• I →X,X ∈(Q,U,V): 仪器起偏(instrumentally induced polarization);

• X →Y,(X,Y)∈(Q,U,V),X /=Y: 仪器引起的偏振交扰(cross-talk);

• X →X,X ∈(Q,U,V): 仪器引起的消偏(depolarization).

其中仪器起偏对应于系统的二向衰减(diattenuation),它增加了入射信号的偏振度,导致伪偏振信号的出现; 偏振交扰表示由系统引起的偏振信号间的相互耦合,它不增加入射信号的偏振度; 消偏表示由系统引起的偏振度降低.

望远镜偏振测量的绝对精度由光子噪声、大气湍流噪声以及仪器偏振效应的不确定性决定.其中仪器偏振的不确定性可由误差矩阵ΔX表征,该矩阵定义了满足偏振测量精度时,望远镜缪勒矩阵各元素的最大不确定性,其表达式为[7]

式中ε为由随机噪声引起的偏振测量误差,a为Stokes参数的比例误差(scale error),Pl与Pc分别为观测目标的最大线偏振和圆偏振信号.根据CGST观测目标可能的磁场特性,我们将以上参数设定为:ε=0.0002,a=0.01,Pl=0.1,Pc=0.1.此时,误差矩阵的数值表达式为

CGST偏振光学的设计目标是: 通过偏振补偿保证望远镜在1µm观测波段,在任意观测方向1＇视场内固有仪器偏振缪勒矩阵的各元素都不超过(3)式所定义的最大误差.

3 CGST的初步光学设计

CGST的光学系统采用三镜对称格里高利设计,如图1所示.望远镜的主镜(M1)和副镜(M2)均采用环形对称结构,其中主镜外径8 m、内径4 m.该对称性保证了主光学系统的偏振中性(polarization neutrality),奠定了CGST高精度偏振测量的基础.热光阑位于主镜焦点处(F1),视场为3＇.望远镜的高度轴位于主镜之后,主光轴向高度轴的转折由一个四镜折轴系统(M4-M7)完成.望远镜的格里高利焦点(F2)位于四镜系统之后.该焦点经中继镜(M3)放大,形成库德焦点(F3).望远镜的出瞳位于中继镜后方,其外径226 mm、内径113 mm,位置刚好与格里高利焦点在空间上重合.在该位置设置有一组中空的交叉折轴镜(M8与M9),它将光束折向望远镜下方的库德房.表1给出了CGST的几何光学设计参数,其中主镜采用抛物面,焦比f/1.46; 副镜为椭球面,放大倍率9.45,出射焦比f/13.8; 中继镜为椭球面,出射焦比f/65.表2展示了当前光学设计在可见光波段(0.5µm)波前像差的Peak-Valley值(PV)和Root-Mean-Square值(RMS).如果以波前像差RMS小于1/14波长作为衍射极限成像质量的判据,那么当前光学设计的理论像质能够满足望远镜在3＇内可见光波段衍射极限成像的像质要求,而图2所示的点列图也证明了这一点.表3列出了望远镜在可见光波段衍射极限成像(1/14波长)的光学容差,这里仅列出了曲面镜的部分(M1、M2、M3).表3中各误差量的方向采用了光学设计软件Zemax的坐标定义惯例.由于该光学容差以主镜坐标系为基准,因此M1无对准误差.

图1 CGST光学结构Fig.1 Optical layout of CGST

图2 CGST库德焦点3＇视场内的点列图,其中圆圈代表波长0.5 µm的艾里斑直径,在每个子图上方标有物方视场坐标(objective coordinates,OBJ),单位为度.Fig.2 The spot diagram of CGST in 3 arc-mins FOV (Field Of View) at the Coud´e focus,where the circle represents the Airy disk for the wavelength of 0.5 µm,while there are OBJ in unit of degree above each subplot.

表1 CGST光学设计参数Table 1 Optical prescription of the CGST

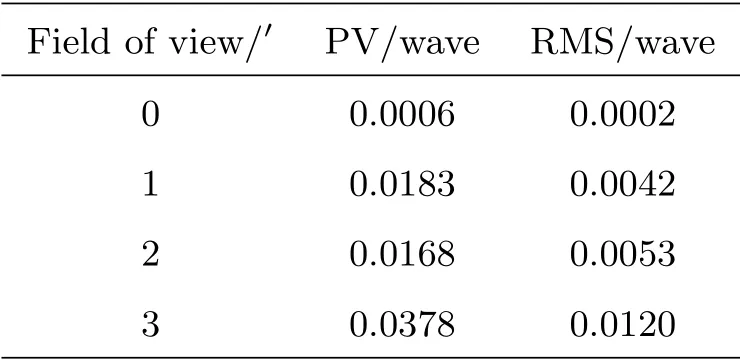
表2 波长0.5µm时,CGST库德焦点波前像差Table 2 Wavefront error at Coud´e focus for the wavelength of 0.5 µm

表3 CGST的光学容差Table 3 The optical tolerance of CGST

CGST的传导光学系统(transfer optics)采用了两组偏振补偿机构,它们分别是由M4至M7构成的四镜折轴系统以及由M8和M9构成的二镜折轴系统,如图3所示.其中的二镜系统是一种经典的偏振补偿机构,它由两块45°入射且方位正交的反射镜构成.第1面镜子的垂直偏振分量(spolarized light)是第2面镜子的平行偏振分量(ppolarized light),它们各自的二向损耗和延迟效应彼此对消,达到偏振补偿的目的.四镜系统是一种新型的偏振补偿光学结构,它由两组相互垂直的五角反射镜(penta mirrors)组成,光束在镜面上的入射角均为22.5°.其偏振补偿原理与二镜系统相同,差别在于五角镜代替了45°反射镜.在望远镜高度角变化时,四镜系统与主光学系统一绕高度轴旋转,其偏振补偿特性不变.与二镜系统相比,四镜系统的一个突出特点是入射光轴与出射光轴在空间相交.该特点避免了二镜系统的光轴平移,保证了镜筒重心与高度轴的重合,降低了望远镜指向结构设计与驱动设计的难度.

图3 CGST传导光路的偏振补偿结构Fig.3 The polarization compensation configuration of transfer optics of CGST

4 偏振模拟方法

4.1 偏振光线追迹

本研究使用的偏振光线追迹程序为一款自主开发的,基于Matlab与Zemax动态数据交换(Dynamic Data Exchange,DDE)的望远镜偏振光学模拟程序,其具有以下3个特点:

•望远镜的几何光学模型在Zemax中定义,金属反射膜的光学模型在Matlab中定义;

•Zemax仅执行几何光线追迹,光线的偏振传递特性由Matlab计算;

•光线的偏振传递特性由琼斯矩阵和缪勒矩阵表征,偏振坐标系被定义在光线上.

望远镜的输入与输出偏振坐标是偏振光线追迹的必要输入,它们由用户自定义.在此,我们要求CGST输入与输出偏振坐标系的+Q方向始终与望远镜高度轴方向平行,-Q方向由+Q与光束传播方向根据右手定则确定.

(4)式展示了偏振光线追迹算法的琼斯矩阵传递方程

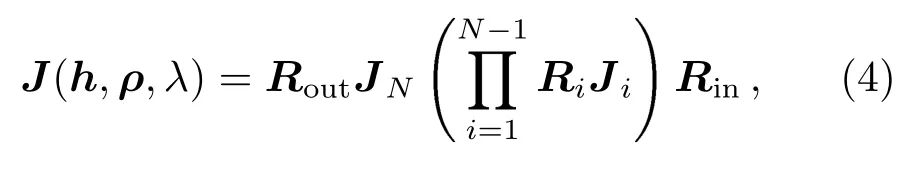
式中左边的J为给定光线的琼斯矩阵,它是光线的像面坐标h=(hx,hy),瞳面坐标ρ=(ρx,ρy)以及波长λ的函数; 式中右边的Ji为光线第i次反射的琼斯矩阵,Ri为第i次反射后的坐标旋转;Rin表示入射偏振坐标向第1次反射的入射面的旋转;Rout表示最后一次反射的入射面向出射偏振坐标系的旋转;N为光线在系统中经过的反射次数.由于镀膜材料的光学特性是波长的函数,因此Ji是波长λ的函数.琼斯矩阵与缪勒矩阵的变换关系[31]如下所示

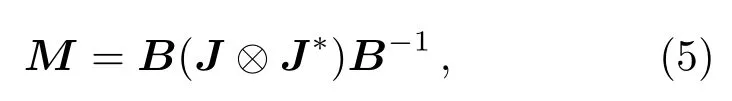
其中⊗为张量积,*为复数共轭,B为常数矩阵

式中j为虚数单位.

4.2 金属膜偏振模型

CGST镜面可能采用的金属反射膜包括: 自然氧化铝膜(Al+Al2O3)、保护铝膜(Al+SiO2或Al+MgF2)或增强金膜.其中前两种膜是主要的考虑对象,它们的膜系结构如图4所示.图中的θi为光线的入射角,h为电介质层(氧化膜或保护膜)厚度,n1、n2、n3分别为空气、电介质层以及金属膜的折射率.由于光学波段电磁波在金属表面下的渗透深度远小于金属镀膜厚度,因此该模型不考虑基底的影响.

图4 金属反射膜的膜系结构Fig.4 The film structure of metallic reflective coating

在金属偏振本征坐标下的琼斯反射矩阵为

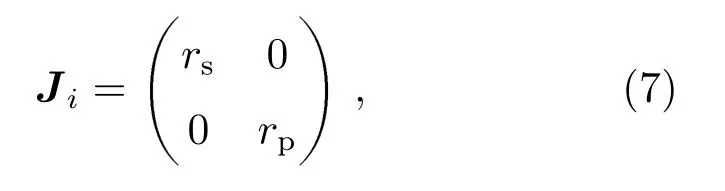
其中rs和rp分别为垂直和平行偏振分量的费涅尔振幅反射系数.利用薄膜光学中的导纳理论[31],我们可以通过入射角、镀膜材料光学常数以及厚度h计算该金属膜的振幅反射系数.铝膜的复折射率是制备工艺、使用环境以及材料老化的函数,在不同的文献和书籍中具有不同的测量和理论值[32-34].此外,铝表面氧化层的厚度目前也没有定论[35-37].为此,我们在实验室使用椭偏仪对铝膜陪镀片的光学常数和氧化层厚度进行了测量,得到氧化层厚度为6.3 nm.表4展示了铝膜和氧化层的光学常数在5条典型太阳大气磁敏谱线波长位置上的测量结果,其中nr和κ分别为铝膜复折射率的实部(实折射率)和虚部(消光系数),nf和κf分别为铝氧化层的折射率实部和虚部.在椭偏测量中,我们同样使用如图4所示的膜系结构进行数据拟合.该模型不考虑氧化层的导电性,因此表4中氧化层消光系数均为零.

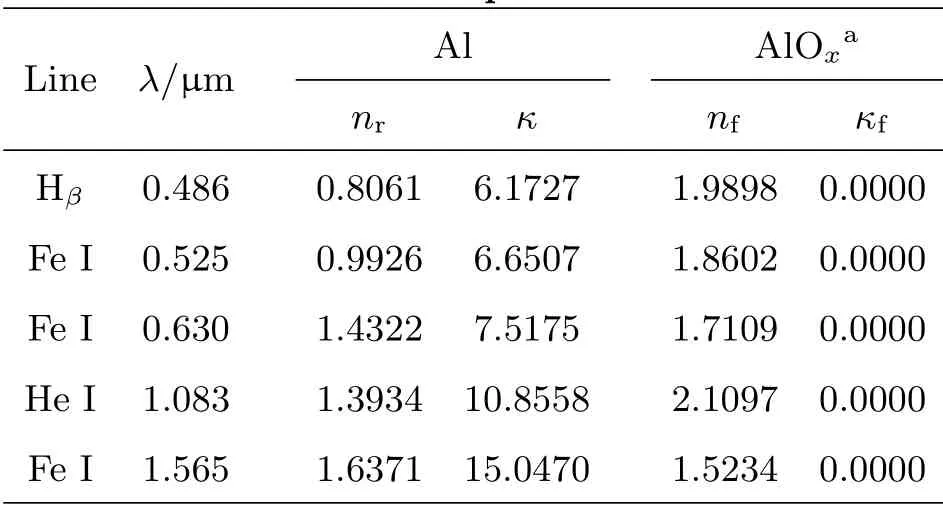
表4 典型太阳大气磁敏谱线波长上铝膜及表面氧化层的光学常数Table 4 Optical constants of the aluminum coating and the aluminum oxide layer for typical magnetic sensitive spectral lines in solar atmosphere

5 偏振模拟结果

5.1 综合仪器矩阵

太阳磁场信号的偏振分析在望远镜像面进行,给定像点上的仪器偏振特性是汇聚于此全部光线的综合效果.在光线非相干叠加的假设下,该点的综合仪器偏振等于全部光线缪勒矩阵的平均,我们定义该平均矩阵为望远镜的“综合仪器矩阵”.望远镜是小像差系统,汇聚于像面一点的光线均来自望远镜光瞳内相同方向的入射光.因此,综合仪器矩阵可由相应视场坐标下的缪勒瞳函数(Muller pupil)积分获得.图5展示了望远镜高度角为90°、方位角0°、观测波长1.083µm时中心视场(hx=0,hy=0)的缪勒瞳函数,其相应的综合仪器矩阵为

图5 CGST中心视场的缪勒瞳,λ=1.083 µm.Fig.5 Muller pupil of CGST in the central FOV,λ=1.083 µm.

该矩阵接近理想的反射单位矩阵,其中最大的非对角矩阵元素为3.02×10-6,远小于(3)式定义的设计要求.进一步的模拟表明,在其他波段中心视场的综合仪器矩阵也都接近于反射单位矩阵.因此,环形孔径并不会影响偏振补偿设计的效果,在整个工作波段CGST库德焦点中心视场都具有偏振中性的特征.

5.2 仪器偏振的视场效应

逐点计算观测视场内的综合仪器矩阵,得到了其在库德焦面上的分布函数.我们将其称之为“视场矩阵”(field of view matrix),F.为突出其是高度角(el)和方位角(az)的函数,在随后的分析中我们将用F(el,az)表示视场矩阵.下面以波长1.083µm为例,讨论CGST全部镜面均为自然氧化铝膜时,视场矩阵的分布特征和指向运动特性.图6展示了望远镜高度角el=90°(指向天顶),方位角az=0°(指向正南)时,3＇视场矩阵的模拟结果.从图中等高线的分布情况来看,其非对角矩阵元素都近于线性函数,而对角元素表现为二次函数的特征.由于对角元素的取值范围远低于0.01的设计要求,因此其视场效应可忽略不计.

图6 CGST指向天顶时,波长1.083 µm的视场矩阵.Fig.6 Field of view matrix for CGST pointing to the zenith at the wavelength of 1.083 µm.

为了方便描述仪器偏振视场效应的强弱程度,我们进一步引入“视场强度矩阵” (Field intensity matrix)的概念.它是一个4×4矩阵,由给定范围内视场矩阵各元素的均方根组成,由字母F表示.(9)式展示了F矩阵元素的形式定义FX→X(X=I,Q,U,V)及其在波长1.083µm,el=90°、az=0°情况下1＇视场内的计算结果.

可以发现,式中除矩阵元素FI↔Q和FV↔U略超过设计要求外,其他矩阵元素均在(3)式所定义的设计要求内.

高度角与方位角是望远镜的运动变量,其中高度角变化引起望远镜内镜子间的相对旋转,而方位角变化则引起整个望远镜光学系统与仪器终端系统的相对旋转.如果把终端系统整体视作一个“偏振分析器”,并已知它的偏振响应矩阵,那么望远镜方位运动仅引起偏振测量坐标系的变化,该效应可通过偏振数据的后处理进行准确的校正.因此,下面仅以高度角为例讨论望远镜运动对视场效应的影响.

模拟指出,高度角变化并不改变视场矩阵的线性分布特征,且视场中心的仪器偏振始终为零.但各矩阵元素的斜率方向会随高度角的变化而旋转,同时部分矩阵元素的斜率也会随之变化.图7展示了不同视场范围内视场强度矩阵的高度角函数,其中虚线表示各矩阵元素的设计要求.从图中可以看出,仪器起偏(I →Q,U,V)和圆偏振向线偏振的串扰(V →Q,U)均不随望远镜的高度角变化.但Q、U向I、Q、U、V的交扰会随高度的增加而先变大后变小或先减小后增大,极值都在高度角45°处出现.为使望远镜能在任意角度下满足仪器偏振的设计要求,我们以视场强度矩阵各元素的最大值作为CGST仪器偏振强度的指标.由这些指标构成的矩阵被称为“最大视场强度矩阵”,其数学形式为

式中max()表示对括号内的矩阵元素求极大值.表5展示了图7中不同视场最大视场强度矩阵的模拟结果,其中那些值远小于设计要求的矩阵元素被略去.从该表可以看出,最大视场强度与视场大小基本符合线性关系,利用该性质可以计算符合偏振设计要求的最大视场.例如,表5中1＇视场上的最强的视场效应来自Q、U与V的交扰,其值为2.2×10-3.根据Q、U、V间偏振交扰不超过2×10-3的设计要求,利用2×10-3/2.2×10-3=0.91,我们得知在波长1.083µm处满足设计要求的最大视场为0.91＇.由于在该视场范围内仪器偏振的视场效应可以忽略,因此我们将该视场称为给定波长的最大无偏振视场(maximum polarization-free field size).表6展示了在1＇视场内5条典型磁敏谱线的最大视场强度矩阵元素.可以发现,一方面,与仪器起偏有关的元素在波长增大的过程中,其视场效应存在先增强后减弱的趋势.另一方面,与偏振交扰有关的元素会一直随波长的增加而降低.这一变化趋势与铝膜复折射率在可见光与近红外波段内的色散轮廓相关.利用表6中的数据,我们进一步计算了CGST在不同波长上的最大无偏振视场,其结果在表7中给出.据此我们得出结论,在可见波段当前偏振光学设计的无偏振视场在0.5＇左右,而在近红外波段CGST无偏振视场增大到了1＇左右.

表5 波长1.083µm时不同视场上视场强度矩阵元素的最大值Table 5 The maximum value of field intensity matrix element at the wavelength of 1.083 µm for different FOV

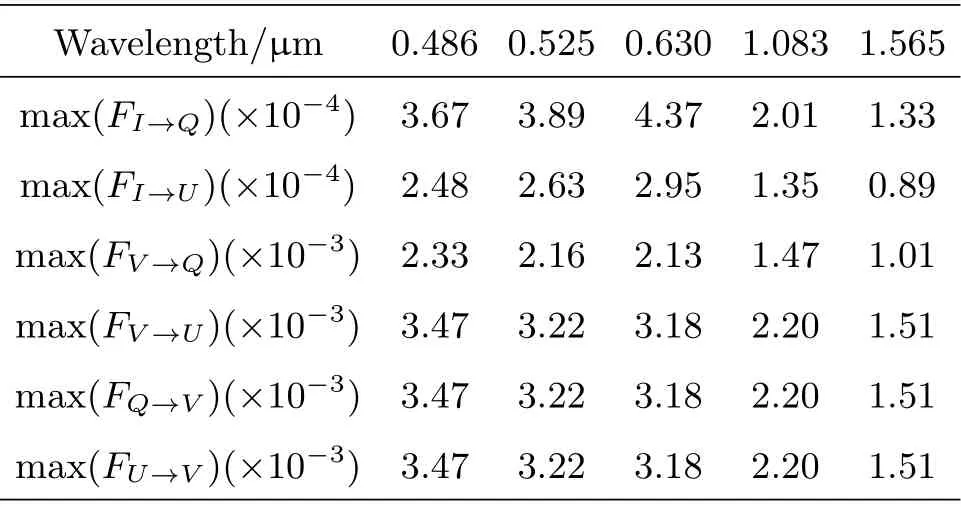
表6 1＇视场内不同波长强度矩阵元素的最大值Table 6 The maximum value of intensity matrix element in an FOV of 1＇ for different wavelengths

表7 CGST不同波长的无偏振视场大小Table 7 The polarization-free field size of CGST in different wavelengths

图7 波长1.083 µm时不同视场范围内的视场强度矩阵元素随望远镜高度角的变化Fig.7 The field intensity matrix for different FOV changes with the elevation angle when the observation wavelength is 1.083 µm

6 结论

CGST偏振光学设计的目标是在近红外波段1＇的观测视场内,任意观测方向上的望远镜固有仪器起偏不超过2×10-4、仪器交扰不超过2×10-3.为此,我们提出了一种基于偏振补偿的光学系统设计方案.该方案具有望远镜的中心视场仪器偏振在任意观测方向和任意波长均为零的特点.该方案中包含了一个独特的四镜偏振补偿结构,与传统的交叉折轴的偏振补偿结构相比,四镜结构实现了主光轴和高度轴的空间相交,解决了折轴系统偏振补偿设计与镜筒结构设计的矛盾.

利用自主开发的偏振光线追迹程序对CGST的光学设计方案进行了建模分析,可知视场效应是CGST仪器偏振的主要问题,它是望远镜角度、波长以及金属薄膜光学特性的函数.仪器偏振在视场上具有线性分布的函数特征,我们将该函数的均方根作为衡量望远镜综合偏振效应的强度指标,并将该强度小于设计要求的视场范围定义为望远镜的最大无偏振视场.结果表明,在He I 1.083µm波段CGST的无偏振视场接近1＇; 在Fe I 1.565µm波段该视场为1.31＇; 而在可见光波段该视场在0.5＇左右.因此,当前的偏振光学设计方案达到了CGST的偏振光学设计要求.

实际望远镜光学系统存在镜面的加工误差、镜面间的对准误差以及金属反射膜光学特性的差异等问题,这些因素都会引起不同程度的偏振效应.作为一台追求衍射极限成像的高分辨望远镜,CGST的光学容差相当严格,即使配备有主动光学和自适应光学系统,其固有的静态像差也被要求在1/10波长以内.对于这样的系统,实际光线与设计的偏离主要表现为光程变化,而非路径与入射角度的变化,因此望远镜的光学误差不会引起明显的仪器偏振变化.我们认为相对于成像质量,仪器偏振对望远镜的镜面加工误差和安装误差并不敏感,其影响可忽略不计.相反,仪器偏振对镜面镀膜的物理特性非常敏感,例如薄膜材料光学特性的均匀性、表面粗糙度甚至灰尘都会产生一定程度的偏振效应.为分析以上问题,我们要在未来的偏振模拟中增加材料光学特性的空间分布特性以及偏振散射的模拟.

目前,CGST的偏振光学设计仍然存在改进和进一步优化的空间.例如,在镜面上可以使用如保护铝膜、增强铝膜这样更为复杂的金属膜系,以提高系统的偏振稳定性和使用寿命.同时,利用材料的选择和膜厚设计可以在特定波长上进一步降低轴外光线的偏振效应,从而扩大无偏振视场的范围.此外,完整的CGST偏振光学设计还应该包含自适应光学系统和终端仪器的偏振设计,进而实现整个偏振测量光学链路的全局优化.本研究使用的偏振光学模拟与分析方法同样可用于其他反射望远镜光学系统的偏振优化设计.

致谢感谢审稿人对文章提出的宝贵建议,使文章的质量有了显著的提高.