生物医学期刊论著中重复测量设计计量资料统计分析和结果表达
李运明,路 强,向雪梅,裴家兴,3,周鹏飞,3,郭 望,2,张瀚博,杨孝光
1.西部战区总医院医疗保障中心信息科,成都 610083; 2.西南交通大学数学学院统计系,成都 611756; 3.西南医科大学公共卫生学院,四川 泸州 646000; 4.西部战区总医院医疗保障中心基础医学实验室,成都 610083
重复测量设计资料,又称为纵向观测资料,是生物医学研究领域中一类重要的研究设计数据,常见于动物行为学实验、人群队列研究、患者随访研究等生物医学研究,包括计量资料、计数资料和等级资料三种类型[1]。各种类型的重复测量设计资料统计分析理论和软件操作方法在医学教材、专著和论文已有阐述[2-4],但在生物医学期刊论著,尤其是国内期刊中,经常发生统计学方法和结果表达上的错误[5-6]。笔者从2019年底开始承担《创伤外科杂志》稿件统计学审稿,也发现类似问题。为提高生物医学期刊论文统计分析质量,本文选取生物医学研究生教材实例,介绍重复测量设计计量资料统计分析和结果表达,以期为该类论著相关内容的撰写提供参考。
1 实例数据
选取人民卫生出版社《医学统计学》第5版[1]第十二章重复测量设计资料的方差分析,例12-3作为本文实例。实例为:某研究者欲比较治疗厌食症的三种不同成分药物的效果,在已构建的厌食症模型大鼠中抽取15只成年雌性大鼠,随机分为3组,每组饲料中添加1种药物,药物有效成分含量相同,连续记录药物治疗前(T0)和治疗后1、3、5、7d的大鼠体重,原始数据见表1。该实例为随机对照实验研究,干预因素为3种不同成分的厌食症治疗药物(A、B、C);重复测量因素为时间,共5个时间点,且相邻时间间隔不全相同;测量指标为计量资料(大鼠体重),因此该研究属于不等距重复测量设计计量资料[2]。
2 统计方法选择
该实例的研究目的(科学问题)是分析干预因素(药物)和重复测量因素(时间)对于大鼠体重的影响,转换为具体研究假设见表2。

表1 不同药物治疗后大鼠体重(单位:g)

表2 不同药物和时间对大鼠体重影响的研究假设
针对表2中具体研究假设,同时考虑该研究不存在缺失数据,选择采用重复测量设计资料方差分析构建相应的检验统计量(F值),并计算P值。根据药物和时间是否存在交互作用,下一步统计分析路径为:
(1)当两者交互作用不具有统计学意义时,只需进行药物和时间的主效应分析。①不考虑测量时间点,直接推断药物对大鼠体重的影响;若药物主效应具有统计学意义时,继续进行两两组间比较。②不考虑药物分组,直接推断时间对大鼠体重的影响;若时间主效应具有统计学意义时,继续进行两两组间比较。
(2)当两者交互作用具有统计学意义时,药物和时间的主效应没有意义,需要进行单独效应分析。①固定重复测量因素水平,开展干预因素单独效应分析,即固定测量时间点,比较3种药物分组大鼠体重均数的差异,并进行两两组间比较。②固定干预因素水平,开展重复测量因素单独效应分析,即固定药物分组,比较5个时间分组大鼠体重均数的差异,并进行两两组间比较。
3 SPSS软件操作
采用SPSS 25.0建立例12-03数据文档,共15行7例数据,见图1。

图1 例12-03 SPSS数据文档
在SPSS Analyze菜单中General Linear Model,调取Repeated Measures…分析窗口,并依次在图2~5中完成变量选择和选项设置,两两组间比较采用Bonferroni方法。

图2 设置重复测量因素和研究指标

图3 选择研究指标和分组因素

图4 选择两两组间比较的因素和方法

图5 设置描述统计和方差齐性检验选项
由于SPSS软件默认结果中不输出单独效应分析结果,需要在程序(Syntax)窗口中修改程序[7]。在图3中,单击Paste按钮,将分析程序输出到程序窗口,按照图6修改“/EMMEANS=TABLES(药物*时间)”语句,以进行药物和时间的单独效应分析。

图6 程序(Syntax)窗口修改“/EMMEANS”语句
4 SPSS输出结果及解释
4.1球对称检验 Mauchly’s检验结果(χ2=6.983,P=0.643),表明不同时间点大鼠体重方差协方差矩阵满足球对称性,不需要对检验统计量进行校正,见表3。

表3 球对称检验结果(Mauchly’s Test of Sphericity)
4.2时间主效应、时间和药物交互作用方差分析结果 因本例数据满足球对称性,时间的主效应、时间和药物交互作用方差分析结果看“Sphericity Assumed”行对应结果,否则需要看校正结果,其中Lower-bound方法校正结果最保守,见表4。时间和药物交互作用检验结果(F=18.105,P<0.001),表明两者交互作用具有统计学意义。因此,时间和药物的主效应无意义,需要进行单独效应分析。假定本例交互作用无统计学意义,时间因素主效应检验结果(F=344.299,P<0.001),表明5个时间点大鼠平均体重不全相等,需要进行两两组间比较。

表4 时间主效应、时间和药物交互作用方差分析表(Tests of Within-Subjects Effects)
4.3药物主效应方差分析结果 药物主效应检验结果(F=5.527,P=0.020),表明3种药物分组大鼠平均体重不全相等,需要进行两两组间比较,见表5。但表4中,时间和药物交互作用存在统计学意义,因此药物主效应无意义,需要进行单独效应分析。

表5 药物主效应方差分析结果(Tests of Between-Subjects Effects)
4.4不考虑测量时间点,药物分组两两组间比较结果 药物主效应具有统计学意义,表明3种药物分组大鼠体重均数不全相等,具体哪两组间存在差异,需要进行两两组间比较。为控制两两组间比较Ⅰ型错误膨胀问题,采用Bonferroni方法对P值校正。A组与C组大鼠体重均数差异具有统计学意义(P=0.018),见表6。但表4中,时间和药物交互作用存在统计学意义,进行药物分组两两组间比较时,需考虑时间因素的影响,因此表6统计结果无意义。

表6 不考虑时间因素,药物分组两两组间比较结果(Pairwise Comparisons)
4.5不考虑药物因素,时间分组两两组间比较结果 时间主效应具有统计学意义,表明5个时间分组大鼠体重均数不全相等,具体哪两组间存在差异,需要进行两两组间比较。治疗后3、5、7d的大鼠体重均数,与治疗前(T0)比较,差异均具有统计学意义(P<0.001)。另外,表7给出了5个时间分组,全部两两组间比较结果。但表4中,时间和药物交互作用存在统计学意义,进行时间分组两两组间比较时,需考虑药物因素的影响,因此表7统计结果也无意义。
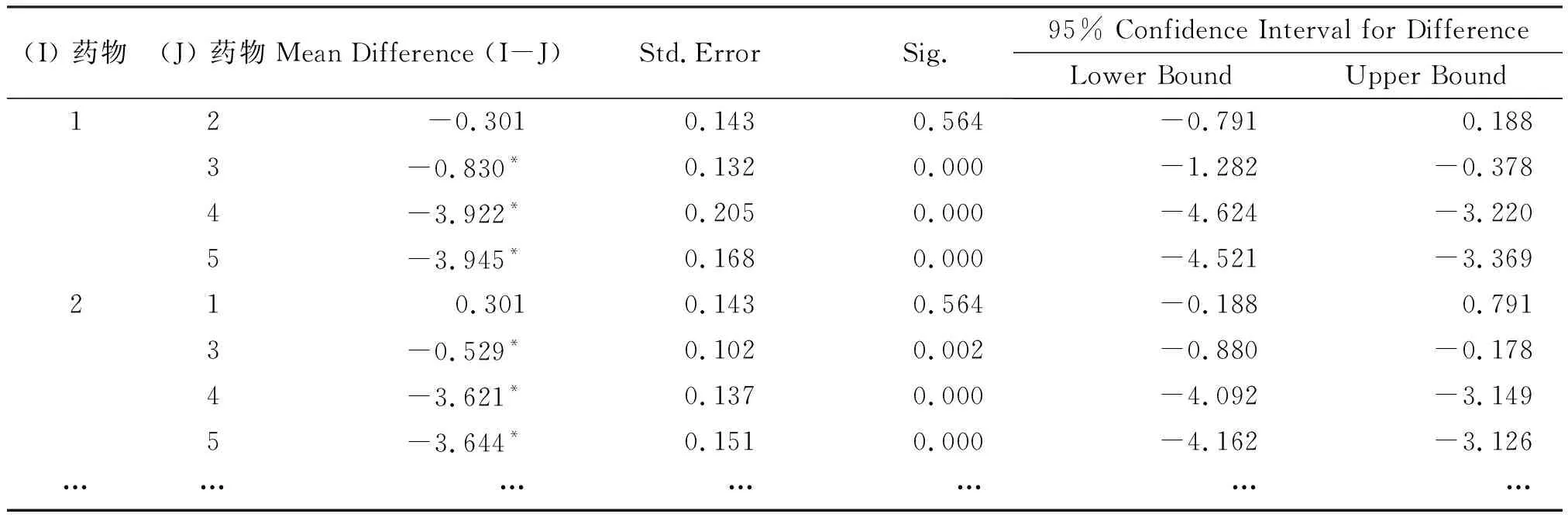
表7 不考虑药物因素,时间分组两两组间比较结果(Pairwise Comparisons)
4.6药物因素单独效应分析 时间和药物交互作用存在统计学意义(表4),需进行药物因素单独效应分析,即:固定测量时间点,比较不同药物分组大鼠体重均数的差异,见表8。治疗前和治疗后3d,3种药物分组大鼠平均体重差异无统计学意义(P>0.05);其他时间点,3种药物分组大鼠体重均数均不全相等(P<0.05),需进行组间两两比较。

表8 药物因素单独效应分析结果(Univariate Tests)
治疗后1d,A组和C组大鼠体重均数差异具有统计学意义(P=0.035);治疗后5d,A组与C组,B组与C组大鼠体重均数差异具有统计学意义(P<0.05);治疗后7d,A组与B组、A组与C组大鼠体重均数差异具有统计学意义(P<0.05),见表9。

表9 固定测量时间点,药物分组两两组间比较结果(Pairwise Comparisons)
4.7时间因素单独效应分析 与表8中药物因素单独效应分析假设检验方法不同,SPSS软件采用多元方差分析进行时间因素单独效应分析,即固定药物分组,比较不同时间分组大鼠体重均数的差异,见表10。分别固定药物分组A、B、C,5个测量时间点上大鼠体重均数均不全相等(P<0.05),需进行两两组间比较。
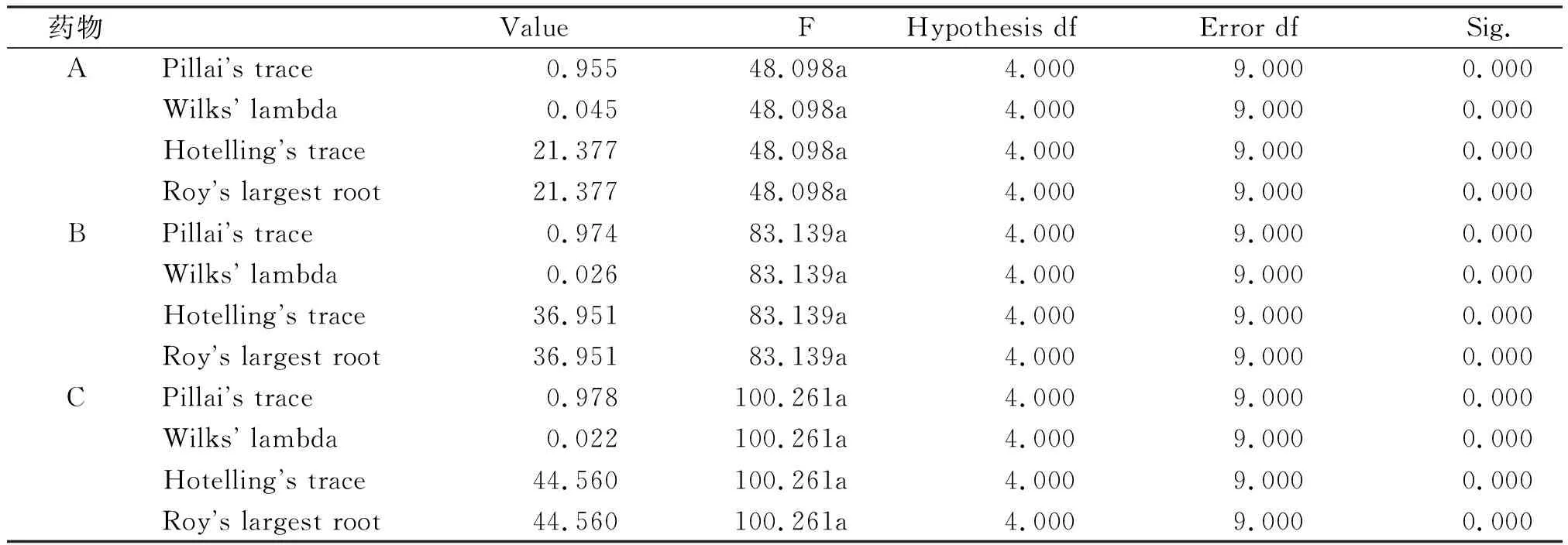
表10 时间因素单独效应分析结果(Multivariate Tests)
药物A分组和药物B分组,治疗后3、5、7d大鼠体重均数,与治疗前比较差异均具有统计学意义(P<0.05);药物C分组,治疗后5、7d大鼠体重均数,与治疗前比较差异均具有统计学意义(P<0.05),见表11。

表11 固定药物分组,时间分组两两组间比较结果(Pairwise Comparisons)
除以上结果外,重复测量设计资料统计分析,SPSS软件输出结果中还包含多元方差分析(Multivariate Tests)、对比检验(Tests of Within-Subjects Contrasts)等其他结果,本文不再赘述,可参考其他文献资料[2-4]。
5 期刊论著中统计学方法表述
论著中资料与方法部分需要描述统计学方法,包含:统计分析软件、统计描述和假设检验方法、检验水准、样本量估计等内容。本实例统计学方法表述如下:采用IBM SPSS Statistics 25.0和Microsoft Office Excel 2016进行统计分析。大鼠体重采用均数±标准差(mean±SD),边际估计均数采用均数±标准误(mean±SE)进行统计学描述。因本研究为重复测量设计,不同药物和时间分组大鼠体重均数组间比较采用重复测量设计资料方差分析,两两组间比较采用Bonferroni方法。采用Mauchly’s方法进行球对称检验,如不满足球对称性,则采用Lower-bound校正。P≤0.05认为差异具有统计学意义。
6 期刊论著中统计分析结果表述
结果部分是期刊论著的主要内容,需要采用精炼的文字、简明的统计表和直观的统计图,反映研究发现的主要结果。重复测量设计计量资料方差分析结果,根据干预因素和重复测量因素是否存在交互作用,结果表述存在较大区别。
6.1干预因素和重复测量因素存在交互作用 经Mauchly’s检验,不同时间点大鼠体重方差协方差矩阵满足球对称性(χ2=6.983,P=0.643)。采用重复测量设计资料方差分析,发现药物分组和时间存在交互作用(F=18.105,P<0.001),需进行药物和时间因素的单独效应分析。治疗前和治疗后3d,3种药物分组大鼠体重均数差异无统计学意义(P>0.05);其他时间点,3种药物分组大鼠体重均数不全相等(P<0.05),两两组间比较结果见表12和图7。治疗后1d,药物C组大鼠体重均数(22.14±0.35)g高于药物A组(20.61±0.79)g;治疗后5d,药物C组大鼠体重均数(26.89±0.83)g高于药物A组(23.99±0.81)g和B组(24.41±0.90)g;治疗后7d,药物B组和C组大鼠体重均数(26.21±0.75g,25.42±0.64g)高于药物A组(23.73±0.64)g,以上组间差异均具有统计学意义(P<0.05)。相同药物分组内,5个时间分组大鼠体重均数均不全相等(P<0.05),与治疗前比较结果见表12和图7。药物A组和B组,治疗后3、5、7d大鼠体重均数均高于治疗前;药物C组,治疗后5、7d大鼠体重均数均高于治疗前;以上组间差异均具有统计学意义(P<0.05)。

表12 不同药物治疗后大鼠体重(g,mean±SD)
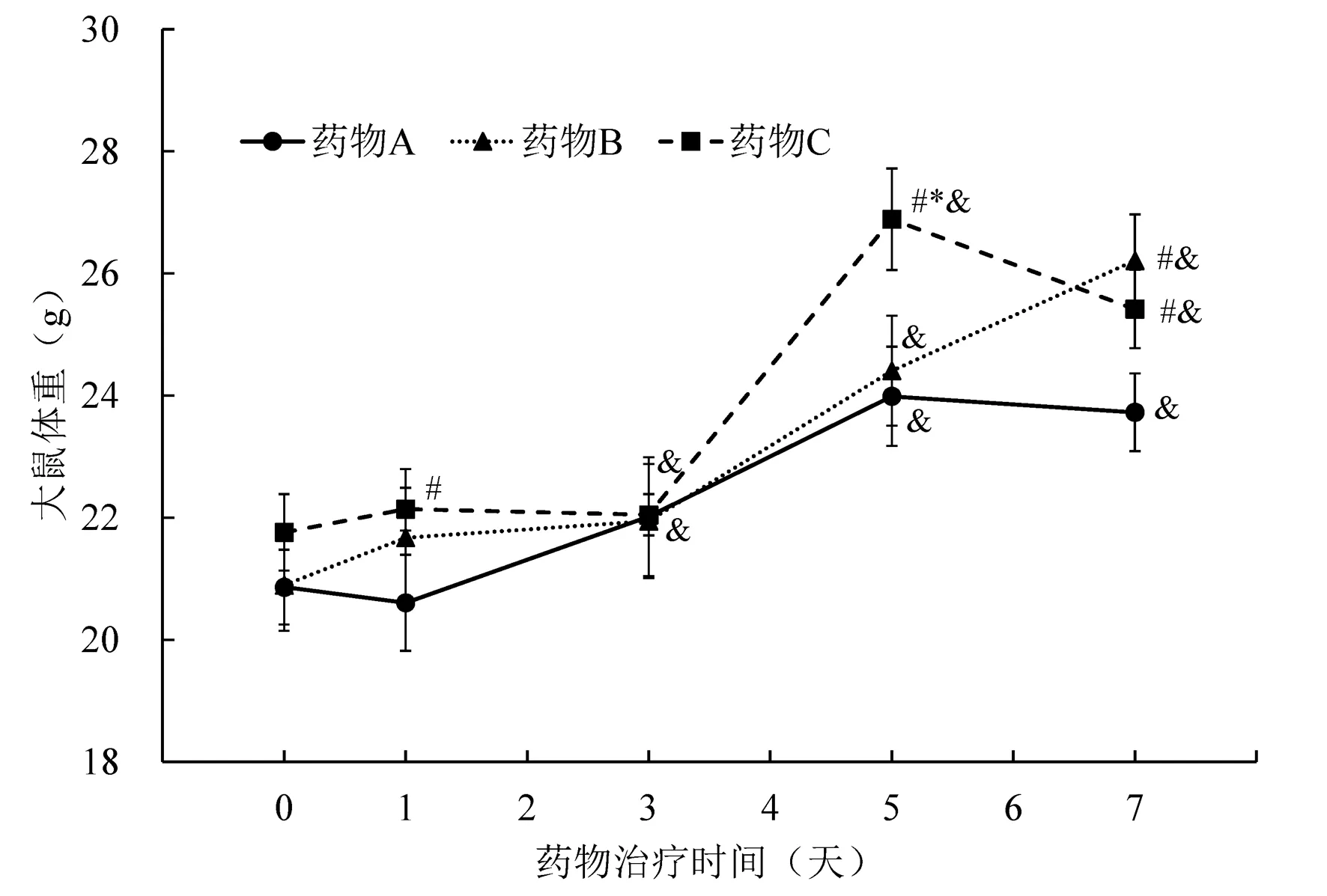
图7 不同药物治疗后大鼠平均体重变化线图
6.2干预因素和重复测量因素不存在交互作用
假定例12-3中,药物和时间不存在交互作用,结果表述如下:经Mauchly’s检验,不同时间点大鼠体重方差协方差矩阵满足球对称性(χ2=6.983,P=0.643)。采用重复测量设计资料方差分析,发现药物分组和时间不存在交互作用(F=X.XXX,P>0.05),不同药物分组大鼠体重均数不全相等(F=5.527,P=0.020),不同时间分组大鼠体重均数也不全相等(F=344.299,P<0.001)。药物C组大鼠体重均数(23.65±0.30)g,高于药物A组(22.24±0.30)g,差异具有统计学意义(P=0.018);药物B组与药物A组、药物C组大鼠体重均数差异无统计学意义(P>0.05),见表13和图8。治疗后3、5、7d大鼠体重均数均高于治疗前,且差异具有统计学意义(P<0.05),见表13和图9。

图8 不同药物治疗后大鼠平均体重
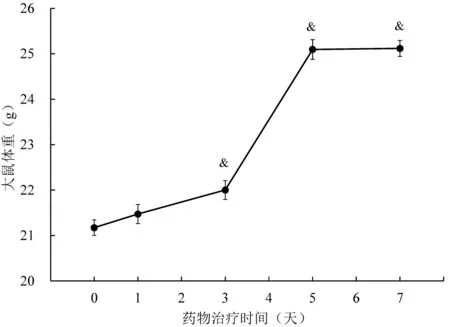
图9 药物治疗后大鼠平均体重变化线图

表13 不同药物治疗后大鼠体重(g)
7 其他类型重复测量设计资料统计分析
7.1其他类型重复测量设计计量资料统计分析 为便于介绍统计方法和结果表达,本文选取了包含3个水平的干预因素和5个水平的重复测量因素实例。除此之外,重复测量设计计量资料还包括:(1)无干预因素,只有重复测量因素;(2)重复测量因素只有2水平,两种常见类型。只有重复测量因素的资料,仍需采用Mauchly’s方法检验球对称性,再采用重复测量设计资料方差分析,然后考察时间因素的主效应,如主效应具有统计学意义,再进行两两组间比较。重复测量因素只有2水平的资料,除不需检验球对称性外,仍需按照重复测量设计计量资料方差分析方法进行统计分析,不能采用配对(伍)设计方差分析。另外,重复测量设计计量资料统计分析还需注意两个问题:(1)绘制统计图时需注意重复测量时间间隔是否相同,SPSS软件“Profile Plots”是按照“观测顺序”输出的统计图,若时间间隔不相等,不能采用该统计图;(2)当部分样本某些时间点存在缺失数据时,可以填补缺失数据后,再采用重复测量设计资料方差分析[8],或采用线性混合效应模型(linear mixed model)[9]。
7.2重复测量设计计数资料和等级资料统计分析 与计量资料相比,重复测量设计计数资料和等级资料在生物医学期刊论著中统计分析方法误用更为严重。首要原因是医学院校本科生和研究生《医学统计学》或《卫生统计学》教材中无相关内容,生物医学研究者不考虑研究设计,遇有计数资料便采用卡方检验,等级资料便采用秩转换的非参数检验。研究设计和资料类型,同时决定统计分析方法。重复测量设计计数资料和等级资料常用统计分析方法包括广义估计方程(generalized estimating equation,GEE)和广义混合效应模型(generalized linear mixed models),具体方法介绍可参考相关专著[9],以及SPSS、SAS等统计软件帮助文件和操作手册。
7.3生物医学研究者应联合医学(生物、卫生)统计学者开展研究 早在1966年,美国医学会杂志(JAMA)编辑部撰文《医学的支柱(A Pillar Of Medicine)》指出:生物统计学家不是令人生畏的检查官,而是生物医学研究者可贵的盟友;生物统计学远非一门无关紧要的数学科学,而是现代医学的一门至关重要的学科,是医学大厦的支柱[10]。在研究设计阶段,生物医学研究者就应该邀请医学统计学者参与,协助根据研究目的明确设计类型、纳入/排除标准、主要/次要研究指标、样本量估计、随机分组/抽样方法、统计分析方法和计划等内容;医学统计学者应全程参与研究过程,检查采集研究数据质量,完成数据统计分析,制作相关统计表和统计图,撰写主要研究结果报告。重复测量设计资料统计分析属于较为复杂的统计分析,需要具备较高的统计学理论和软件操作技能,因此生物医学研究者应积极寻求医学统计学者的帮助。
作者贡献声明:李运明:研究设计、统计分析、论文撰写;路强、向学梅、张瀚博:论文修改、文献检索;裴家兴、周鹏飞、郭望:统计分析、论文修改;杨孝光:研究指导、论文修改、经费支持;