硅钢片固结方式对新能源汽车电机模态特性影响的研究
宋金元,蒋伟康
(上海交通大学 机械与动力工程学院,上海 200240)
电机是新能源汽车的主要噪声源之一,近年来成为电机研究的热点。定子铁芯是电机噪声的主要噪声源,而定子的辐射噪声主要是由于激励力频率与定子固有频率相同而引起的共振[1-2]。定子铁心叠片结构的常见固结方式包括粘接和焊接两种,均可能影响定子的固有频率与模态振型。因此,可以通过优化定子的固结工艺,改善定子的振动特性,以达到电机减振降噪的目的。
针对定子铁芯粘接的固结方式,Kaimori等[3]基于有限元开发的均质化方法模拟叠层,实验与仿真的结果表明,该均质化技术可以应用于铁芯低频磁场的计算问题。Luchscheider等[4-5]通过准静态测试识别了定子叠片结构的接触刚度,基于实验提出了不同的接触模型,并对电动机的准静态行为进行改进的仿真。在接触模型的帮助下,可以使用多尺度方法创建材料模型。Baloglu等[6]提出了一种均质化技术,将定子叠片等效成线性化的横向各向同性模型,保证了计算效率。Pupadubsin等[7]将铁芯视为层叠结构,介绍了用于定子叠片铁芯和线圈绕组的杨氏模量估计的技术。开发了一种半有限元方法技术,用于计算层压芯材的杨氏模量。邓文哲等[8]通过模态实验识别出定子铁芯的各向异性参数,基此建立的定子有限元模型与实验结果误差在3%以内。
定子铁芯焊接的固结方式的既有研究主要关注强度,已有的研究内容包括:顾磊等[9]建立了一个跨度为6 m的包含焊接空心球节点的精细化网壳模型,研究了网壳的频谱特性、水平和三向地震作用下的承载力,以及节点壁厚变化对动力极限承载力的影响。Nielsen等[10]从电-热-机械耦合的基础出发,介绍了电阻焊接的有限元实现和三维建模的方法。Wang等[11]实验探究了一种电工钢的焊接性能,结果表明焊接叠片的抗扭强度与焊缝面积呈线性关系。
上述研究中,对粘接铁芯的研究主要集中在对叠层结构的建模分析,主要探究焊接工艺对铁芯的静态机械性能影响,而铁芯固结方式对其动力学特性的影响还未可知。因此,本文提出了粘接和焊接两种连结工艺的动力学建模方式,设计了定子铁芯的模态实验,验证本文这两种连结工艺的定子动力学建模的准确性,分析了焊缝数量对定子固有频率影响规律,提出了定子的降噪设计建议。
1 两种固结工艺定子的动力学建模方法
1.1 粘接定子的建模方法
粘接是电机定子的常用固结工艺,定子硅钢片分组,组内硅钢片之间用粘接剂粘合,并用液压机组装,叠片叠层在压力下烘烤、冷却,即可成型。
定子铁芯可以视为由硅钢片和绝缘粘接剂组成的复合材料,结构如图1所示。其中z方向表示定子铁芯的轴向,x,y方向为铁芯的面内方向。

图1 叠片结构模型Fig.1 Model of bonded stator
受到粘接剂的影响,定子铁芯不是各向同性的连续均质体,本文对粘接定子动力学建模的假设为:(1) 定子铁芯中的硅钢材料与粘接剂都是各向同性的连续体。(2) 定子整体表现出明显的正交各向异性[12]。(3) 硅钢片与粘接剂相连节点处位移相同。定子叠片的等效材料参数计算基于经典叠片理论[13]。假设粘接剂的体积分数为δ。则定子铁芯的密度可以表示为
ρ=ρs(1-δ)+ρgδ
(1)
式中:ρ表示质量密度;下标s表示硅钢材料;g表示粘接剂。
面内方向(xy方向)上的杨氏模量为
Ex=Ey=Es(1-δ)+Egδ≈Es
(2)
轴向(z方向)上的弹性模量为
(3)
xy方向上的泊松比为
νxy=νs(1-δ)+νgδ
(4)
z方向上的泊松比为
(5)
根据材料的弹性模量与泊松比可以计算其剪切模量,剪切模量包括Gxy,Gxz,Gyz面内方向的弹性模量(Gxy)即硅钢材料的剪切模量。由于定子的结构对称性,对于定子铁芯:Gxz=Gyz,但受到固结工艺的影响,该数值会明显小于硅钢材料的剪切模量。
本文所分析的粘接定子的叠片铁芯型号为某牌号高磁感应强度的各向同性电工钢,主要用于生产定子铁芯。硅钢片和粘接剂的材料特性数据如表1所示。
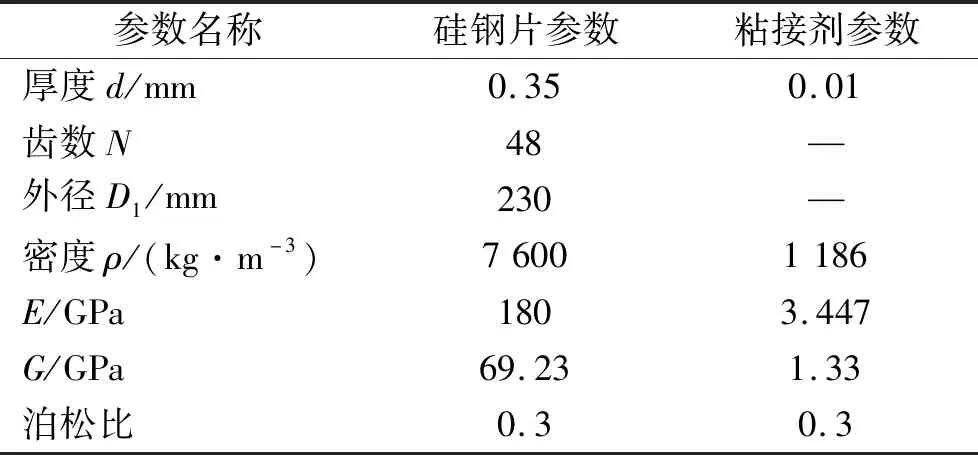
表1 硅钢片与粘接剂材料参数Tab.1 Material property of silicon steel and its adhesive
本文用连续定子模型的正交各向异性来表征定子层叠方向的机械性能,将定子铁芯等效为正交各向异性连续实体结构。通过硅钢片数目与单片厚度的乘积可以获得硅钢片总厚度,然后测量粘接实验定子的总厚度,二者的比值为硅钢材料的体积分数。根据式(1)~(5)与表1的数据,可以计算得粘接定子正交各向异性等效机械性能参数,如表2所示。
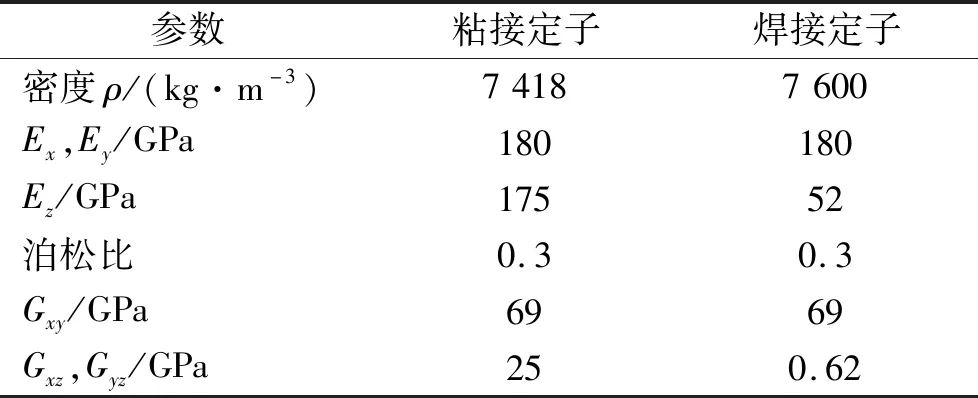
表2 定子铁芯正交各向异性参数Tab.2 Orthotropic parameters of the stator
1.2 焊接定子的建模方法
焊接也是定子常用固结工艺,首先将硅钢片堆叠成型,用液压机固定,再用连续激光焊接的方式沿铁芯的焊缝,从上至下将硅钢片焊接在一起[14]。定子焊接模型如图2所示。
焊接定子简化为激光焊缝的连续梁与硅钢片的组合,硅钢片与焊缝在连接处节点的位移相同。

图2 焊接定子叠片模型Fig.2 Model of welded stator
由于不同硅钢片之间、焊缝与硅钢片之间接触数量庞大,直接对定子焊接模型进行动力学求解将耗费大量内存资源与时间成本。而硅钢片之间仅有焊缝连接,因此假设焊接的定子铁芯也呈现出正交各向异性。与粘接定子的处理方式相同,同样将焊接定子等效为正交各向异性的连续实体结构。假设硅钢片和焊接梁都是各向同性材料。xy方向上的材料参数与硅钢片相同。z方向上的材料参数通过半有限元的方法,基于静力学方法求解焊接定子模型各个方向的弹性模量。
图3是计算z方向杨氏模量力学模型。焊接定子一端固定,另一端施加均匀拉伸应力。根据软件计算出的轴向拉伸应变,基于广义胡克定律即可求解出焊接定子轴向的杨氏模量。焊接定子剪切模量的计算方法与拉伸模量相似,只是将拉伸应力修改为剪切应力,计算出焊接定子整体的剪切变形,进而求出定子xz与yz方向的剪切模量。
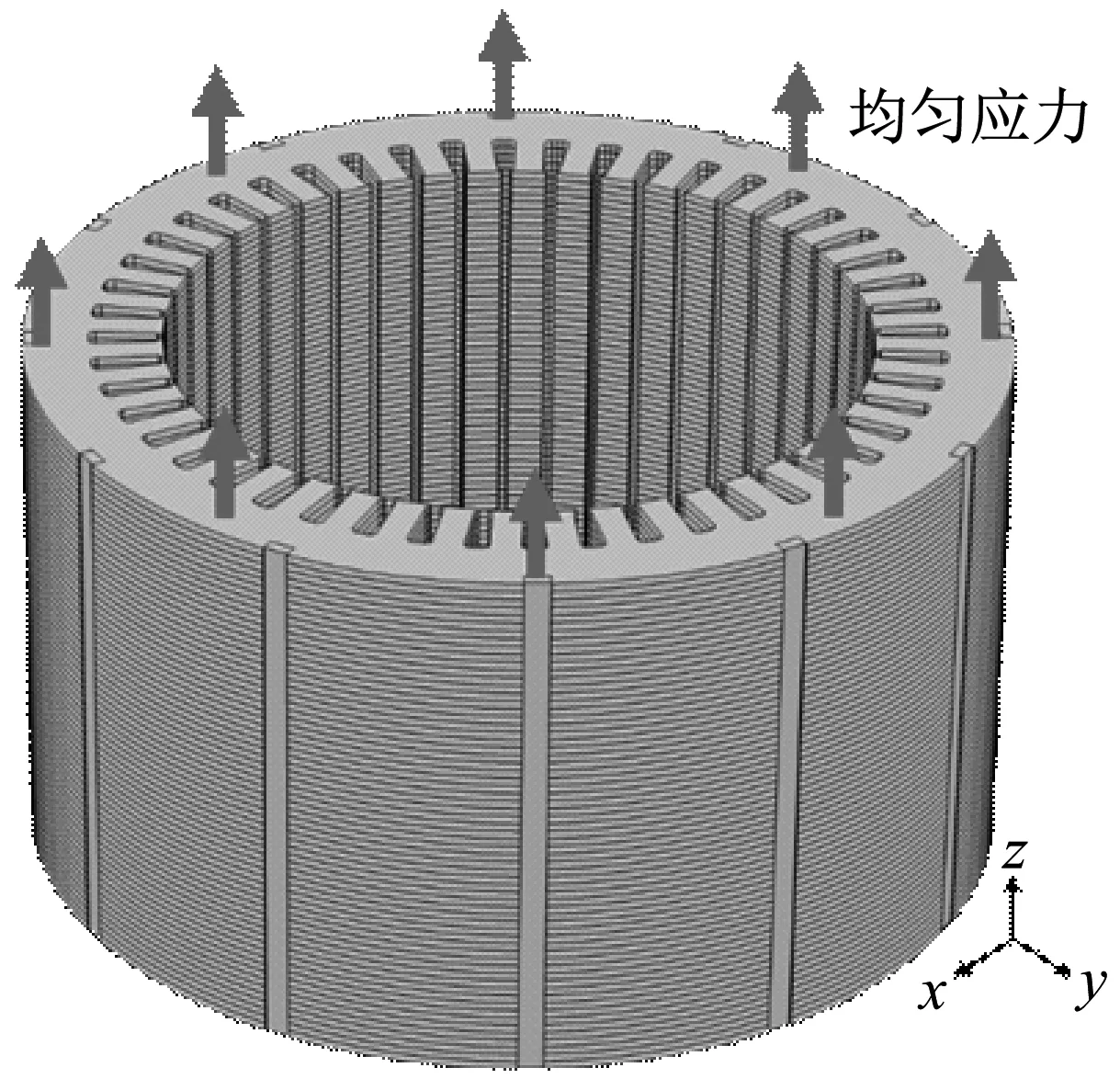
图3 等效轴向杨氏模量的计算Fig.3 The model for calculation of equivalent Young’s modulus on z direction
仍采用与上节粘接定子相同的硅钢片。定子的焊缝数量为12条,焊缝尺寸通过测量实验定子获得。钢片之间的间隙可以忽略,钢片之间光滑无摩擦,可以发生横向滑移。焊缝与硅钢片的材料特性相同。所以焊接定子的表观密度等于硅钢材料密度,其面内方向的杨氏模量与硅钢材料相同。其余模量通过半有限元方法求解,最终计算出的焊接定子正交各向异性参数见表2。
由表2可知,不同固结方式主要影响定子铁芯的轴向弹性模量与xz、yz方向的剪切模量。数值上硅钢片的模量大于粘接定子的模量,而焊接定子的模量最小。
2 两种固结工艺定子的模态分析
2.1 定子振动模态的数值分析
本文对铁芯的层叠属性通过材料的各向异性来表征,将定子铁芯等效成连续的实体结构。其有限元模型如图4所示。

图4 定子铁芯等效有限元模型Fig.4 The homogeneity finite element model of stator core
将表2的等效各向异性参数赋予有限元模型,模型是自由的边界条件,有限元计算出的粘接与焊接定子的固有频率与模态振型如表3所示。
由表3可知,受固结方式影响,粘接定子的固有频率要大于焊接定子的固有频率,同时粘接定子与焊接定子的模态振型也有所区别。对节径数m=0的模态影响较小,因为粘接定子与焊接定子在x与y方向上的等效刚度一致。但是由于焊接定子的在xz与yz方向的弯曲刚度远远小于焊接定子,因此节径数m=2的粘接定子模态频率要大于焊接定子m=2的模态频率,这也就导致了焊接定子的第一阶模态的节径数为1。受固结方式影响最大的是扭转模态,数值上粘接定子固有频率远远大于焊接定子。
2.2 定子的实验模态分析
为了验证定子建模的准确性,对由上一章的硅钢材料构成的粘接定子和焊接定子进行了模态实验。硅钢片的材料参数见表1,两种不同固结工艺的定子实物图如图5所示。
本文定子模态实验的分析方法是锤击法,采用单点激励多点拾取(SIMO)的方法。为了充分激发定子的高频模态而选用钢头力锤,定子铁芯的模态测试现场如图6所示。

表3 有限元计算结果Tab.3 Finite element results

(a) 粘接定子铁芯

图6 定子铁芯模态测试现场图Fig.6 Modal test site of stator core
实验测量获得电机外壳表面测点的传递函数,并经过模态识别获得定子的前几阶结构模态的固有频率和振型。最终实验获取了两种不同定子的前5阶固有频率,结果如表4所示,定子的模态振型与仿真结果一致,见表2。
为了得到固结工艺对定子铁芯动力学的影响规律。本文除了对表2中的两种定子铁芯进行有限元计算,作为对照,对各向同性的定子连续体也进行了模态计算。有限元计算的结果与实验结果的对比如表4所示。
由表4可知,固结工艺对定子固有频率影响巨大。实际定子铁芯的固有频率远小于各向同性连续定子模型的计算结果。对比两种固结方式的定子模态仿真值与实测值,除了焊接定子第五阶模态误差达到4.5%以外,其余误差均控制在2%以内。说明本文提出的定子铁芯的正交各向异性连续体模型可以准确估算定子铁芯的动力学特性。但是由于本文的有限元计算没有考虑阻尼,仿真结果应稍高与实验结果,但是表4中部分实验结果却大于有限元结果,本文认为可能是模态实验期间,力锤的激励点与幅值无法保证相同,且根据频率响应函数选择固有频率也容易产生误差,最终导致这种情况的产生,但由于误差很小,在工程可接受范围内。因此本模型计算快捷,修改方便,在定子设计之初即可准确估计定子的动力学特性。可用于指导电机定子设计。

表4 定子模态有限元与实验结果对比Tab.4 Comparative results of the resonant frequency between numerical and Experimental results
当节径m=0时,两种定子的模态频率与对照的仿真结果相差最大为3%,可见固结工艺对定子周向模态影响很小。但当m=1时,各向同性定子铁芯的仿真结果要大于粘接定子固有频率实测值,焊接定子固有频率实测值数值最小。因此,定子的固结工艺主要影响定子铁芯节径数目不同的模态。固结方式影响定子的动力学特性,若需研究定子的振动响应,固结方式是必须考虑的工艺因素。
3 焊接定子的低噪声工艺设计
降低电机振动噪声的两个主要措施为:①将定子结构设计成具有尽可能高的固有频率,避免与低频的电磁激励力共振[15];②控制励磁力以减小力谐波的幅度。这里讨论如何通过优化焊缝布置,降低电机噪声的方法。
对于焊接定子,从以上章节分析,可以看到焊缝的数量直接影响定子的刚度,进而影响定子的固有频率。为了探究焊缝数量对定子动力学特性的影响,用本文提出的建模方法,研究焊缝数量对定子固有频率的影响规律。其中,焊缝数量为4、8、12、16、20的定子正交各向异性参数如表5所示,固有频率如图7所示。

表5 不同焊缝数目定子正交各向异性参数Tab.5 Orthotropy parameters of welded stators with different welds
由表5可知,焊缝的数目主要影响定子轴向的杨氏模量与和轴向相关的剪切模量的数值,进而影响到定子的动力学特性。由图7可知,焊缝数目主要影响m=1与扭转的模态频率,焊缝数目与模态频率呈正相关。
在电机的低噪声设计上,电机一般不会超过额定转速。当激励主频低于固有频率时,根据振动系统的频响特性,转速降低后,激励频率随之降低,激励幅值一般变小,振动响应就更小了。所以,额定转速是匀速运行时,振动噪声最严重的工况。而瞬态加速时,噪声比匀速行驶时高,但乘员对加速噪声不敏感,甚至还追求“动力感”。因此本文主要针对实验电机额定转速工况展开分析。

(a) 径向模态
由实验定子组成的电机额定转速为n=6 000 r/min,电机的极对数p=3,对应的绕组基频为f=pn/60=300 Hz。则电磁激励力主要包含绕组基频300 Hz以及基频整数倍的谐波信号。16、20条焊缝的定子的(1,2)、(0,3)、扭转模态的固有频率分别接近600 Hz、1 800 Hz。那么,实验定子的焊缝数目设计成8或者12条是合理的。由于本文分析的实验定子实际具有12条焊缝,符合本文的分析结论,而由于焊缝数目不变,电机的电磁性能与机械性能基本没有改变。所以,为了设计低噪声电机,焊接定子的焊缝数目是必须考虑在内的。
4 结 论
本文对两种不同固结工艺定子铁芯进行了研究。提出了两种定子铁芯的建模方式,通过实验修正了有限元模型,最终有限元结果与实验结果相吻合。可以得出如下结论:
(1) 粘接定子的材料特性可以根据经典叠片理论进行计算,表现出明显的正交各向异性。
(2) 焊接定子同样表现出正交各向异性。本文提出的半有限元方法可以对焊接定子进行准确的动力学建模。
(3) 定子的固结方式主要影响定子铁芯节径数目不同的模态,对节圆数目不同的模态影响很小,对焊接定子扭转模态影响很大。焊接定子的固有频率要小于粘接定子的固有频率。
(4) 以实验定子组成的电机为例,基于本文提出的方法推断出定子的最佳焊缝数目为8条或者12条。本文提出的焊接定子建模技术可用于指导电机设计。

