球缺型EFP毁伤混凝土墙试验与数值仿真研究
郝礼楷,顾文彬,张亚栋,原 奇,邹绍昕,刘明君,刘森琪
(1.陆军工程大学 野战工程学院,南京 210000;2.31539部队,北京 100000;3.东南大学 爆炸安全防护教育部工程研究中心,南京 210000;4.西南科技大学,四川 绵阳 621000;5.陆军工程大学 国防工程学院,南京 210000)
混凝土在军事设施中广泛使用,对混凝土类目标的毁伤破坏在装备研制和工程防护等领域是长期受关注的热点问题。聚能装药主要包括聚能射流(shaped charge jet,JET)、聚能杆式弹丸(jetting projectile charge,JPC)和爆炸成型弹丸(explosively formed projectile,EFP),能够在混凝土靶表面形成具有较大直径和一定深度的漏斗坑,并在混凝土内部形成侵彻孔洞[1],是毁伤混凝土类目标的常用方法。聚能装药打击混凝土类目标所产生的漏斗坑大小、侵彻孔径及侵彻深度都是毁伤效果的重要评价指标,众多学者对侵彻深度和侵彻孔径给予重点关注,一些研究工作的重点同样是在保证侵彻深度的基础上提高侵彻孔径[2-4]。与聚能射流(JET)和聚能杆式弹丸(JPC)相比,爆炸成型弹丸(EFP) 具有稳定性好、速度梯度小和后效作用大等优点,其产生的漏斗坑相对而言具有较高深度和较大直径[5]。同时,EFP能够在较小炸高处形成有效侵彻体,加以利用可对混凝土结构造成高速侵彻及爆炸冲击波的耦合毁伤。深入研究EFP装药作用下混凝土结构的毁伤机理,对于聚能装药结构优化、防护结构设计等均具有重要意义。
EFP通常可以由大锥角、球缺罩等药型罩经过翻转闭合形成[6],众多研究人员已经开展EFP装药侵彻混凝土靶的研究。许香照等[7]开展大锥角EFP侵彻混凝土靶的数值仿真研究,结果表明随着锥角增大,侵彻深度减小,侵彻孔径增大。Hu等[8]研究炸药类型、药型罩结构和靶板结构等因素对EFP侵彻效果的影响,表明紫铜药型罩在开坑、侵彻孔径和侵彻深度等方面均优于硬铝罩,锥形和截顶罩EFP开孔深度较大但直径较小。段建等[9]开展大锥角和球缺型EFP侵彻混凝土靶试验,分析了侵彻孔径与深度的关系。在漏斗坑研究方面,Wang等[10]开展了多组大锥角EFP侵彻混凝土靶试验,获得不同药型罩材料及结构、不同装药直径和不同炸高下的侵彻试验数据,总结了漏斗坑直径和深度的变化规律。
目前关于EFP侵彻混凝土的研究工作大多关注于侵彻深度和侵彻孔径,对漏斗坑的研究较少,缺乏对漏斗坑毁伤机理的深入认识,且有关球缺型EFP装药形成漏斗坑研究方面的公开报道更加有限。同时,现有EFP装药侵彻混凝土靶大多开展的是缩比试验,靶体尺寸较小[11]。由于混凝土材料具有显著的结构特征,不同缩比尺寸混凝土靶的试验数据之间存在明显尺寸效应,开展大尺寸混凝土靶侵彻研究,对于理论研究和实际应用都是很有必要的。此外,已有聚能装药侵彻混凝土靶的研究以炸高较大的情况为主,重点关注聚能侵彻体的侵彻破坏效应,装药近炸时爆炸冲击波与聚能体侵彻对目标的联合毁伤问题研究尚未见公开报道,但在工程实际中却是不可忽视的一项重要内容。
本文设计一种Φ120 mm口径的球缺型EFP装药,分析了不同炸高下EFP成型规律,确定了装药侵彻混凝土墙试验的有效炸高。基于修正参数的RHT模型进行侵彻数值仿真,分析炸高对漏斗坑直径和深度的影响规律。在此基础上,对EFP近炸作用下侵彻和爆炸冲击波对混凝土墙的联合毁伤效应进行初步探讨。
1 EFP装药及其成型仿真
EFP不同炸高下的成型形态是确定试验炸高的重要依据,同时准确模拟EFP成型是开展混凝土墙侵彻毁伤仿真分析的基础,首先对EFP成型过程进行仿真模拟。
1.1 EFP装药结构
设计了一种Φ120 mm口径球缺型EFP聚能装药。如图1所示,主装药为压装JH-2炸药,使用船尾形装药结构;药型罩材料为紫铜,使用球缺型变壁厚结构。药型罩整体厚度由罩顶厚δ确定,壁厚变化梯度由内曲率半径r1和外曲率半径r2确定。加工2枚无壳体EFP聚能装药进行试验。
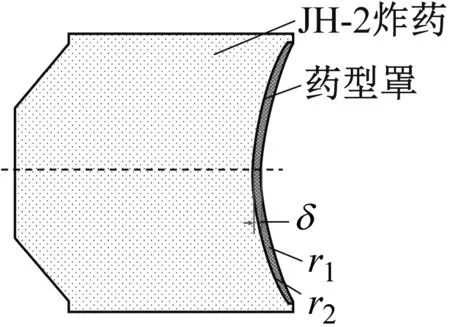
(a) EFP装药结构剖面
1.2 EFP成型数值仿真
1.2.1 数值模型
EFP数值仿真模型由药型罩、炸药和空气三部分构成。考虑到模型的对称性和减小计算量,在LS-DYNA软件中建立二维轴对称有限元模型,在模型的对称面上设置对称约束,对空气域外围边界施加透射边界条件。起爆点位于主装药上端面中心处,计算采用cm-g-μs单位制。药型罩、炸药、空气均采用多物质ALE算法描述。
药型罩材料为紫铜,采用MAT_JOHNSON-COOK模型和EOS_Gruneisen状态方程描述;炸药为JH-2炸药,采用MAT_HIGH_EXPLOSIVE_BURN模型和EOS_JWL状态方程描述;空气采用MAT_NULL模型和EOS_LINEAR_POLYNOMIAL状态方程描述。各材料参数取值如表1~表3所示。

表1 空气材料参数[12]Tab.1 Material parameters of air
数值仿真结果的准确性不仅取决于材料模型参数,对网格尺寸也十分敏感。经过大量网格敏感性分析工作,对于上述模型及算法,网格尺寸需控制在1 mm以内,药型罩至少划分4层网格。

表2 JH-2炸药材料参数[13]Tab.2 Material parameters of JH-2 explosive

表3 紫铜材料参数[14]Tab.3 Material parameters of red copper
1.2.2 模型校核
为校核本文数值仿真模型的正确性,采用相同的建模方法和材料模型,对按图1中装药结构进行局部等比例缩小的Φ65 mm EFP装药[15]的试验结果进行分析验证。
将数值仿真得到的EFP外形与试验X光照片进行对比,如图2所示。由图2可知,除EFP尾部外,数值仿真和试验得到的EFP形状及尺寸均吻合良好,试验结果中EFP的马鞍形收缩在数值仿真中得到很好体现,表明所建立的数值模型能够有效模拟EFP速度的变化过程和速度梯度。Φ65 mm EFP的速度v、长度L、前部最大直径D1、中部最大直径D2和长径比L/D2的数值仿真结果与X光试验结果对比如表4所示。由表4可知,两者最大误差6.69 %,表明数值仿真模型和材料参数合理,仿真结果可信。

图2 Φ65 mm EFP成型数值仿真与X光试验对比Fig.2 Comparison of the simulated shape with and X-ray test ones of the Φ65 mm EFP
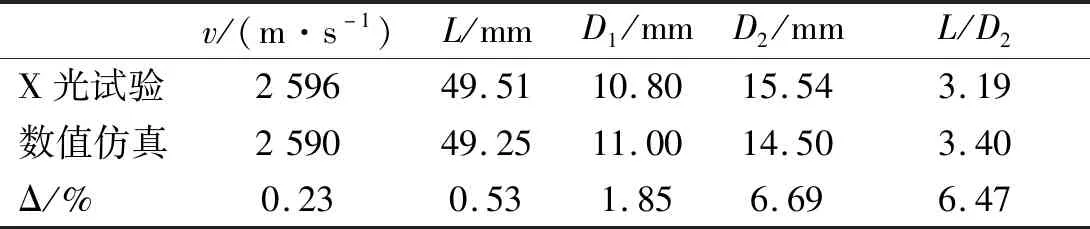
表4 Φ65 mm EFP数值仿真结果与试验结果对比Tab.4 Comparison of numerical results with test of the Φ65 mm EFP
1.2.3 不同炸高下EFP成型形态
图3是不同炸高下Φ120 mm EFP成型的数值仿真结果,表5、图4和图5分别给出相应的EFP特征参数及曲线,其中H代表炸高、v1代表EFP头部速度、v2代表EFP尾部速度,v3代表头尾速度差,L代表EFP长度,D代表EFP中部最大直径,L/D代表EFP长径比。
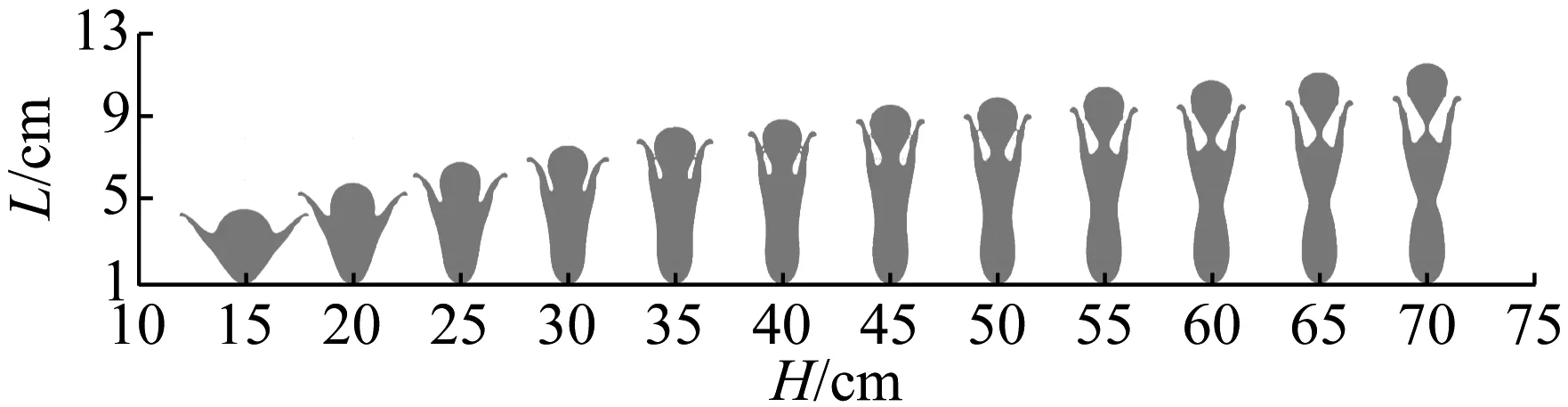
图3 Φ120 mm EFP不同炸高下的成型变化Fig.3 Morphological changes of the Φ120 mm EFP under different standoff distances
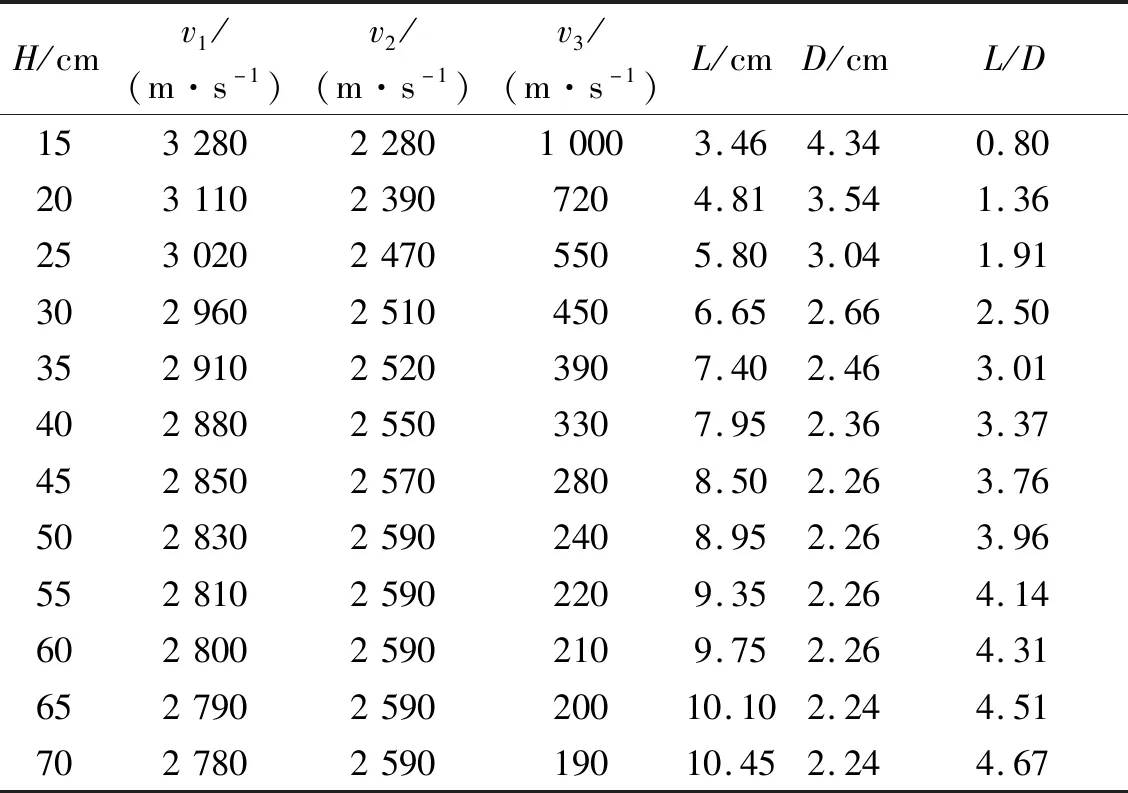
表5 Φ120 mm EFP成型数值仿真结果Tab.5 Numerical simulation results of the Φ120 mm EFP

图4 Φ120 mm EFP头部、尾部速度和速度差随炸高变化Fig.4 Head velocity,tail velocity,and their difference of the Φ120 mm EFP with standoff distances

图5 Φ120 mm EFP长度、中部直径和长径比随炸高变化Fig.5 Length,middle diameter,and length-diameter ratio of the Φ120 mm EFP with standoff distances
如图3首先可以看到,本文EFP装药在比较大的炸高范围内均能获得稳定、连续的EFP侵彻体,表明本文设计的EFP装药结构非常有效。表5、图4和图5的定量分析表明,随着炸高的增大,EFP头部速度、头尾速度差和EFP中部直径逐渐减小,EFP尾部速度和长径比逐渐增大,以上变化趋势随炸高增大逐渐减小并最后趋于稳定。
为获得较大直径和深度的漏斗坑,EFP撞击混凝土墙体时的最佳形态应该是头部速度较大且头尾速度差较小,长径比适中,头部直径较大且形态密实。分析表明,本文设计的EFP在炸高增大到30 cm时,头部开始出现径缩,且随着炸高的增大径缩越来越明显;当炸高达到55 cm时,EFP尾部开始产生断裂,且头部的径缩也愈加增大,头部也将开始产生断裂,这些径缩和断裂将导致EFP的不稳定侵彻,使侵彻效果降低。根据上述不同炸高下的EFP成型形态分析,试验炸高确定为30 cm和45 cm。其中,炸高为30 cm时,EFP呈现短粗的形态,密实度较好且头部速度较大;炸高为45 cm时,EFP头部速度和头尾速度差已经趋于稳定,且长径比适中,形态稳定。
2 侵彻试验
2.1 混凝土墙结构与试验布置
试验靶体混凝土墙体结构,如图6所示。该墙体由上、下两个部分组成,采用C35混凝土浇筑,内部配有构造钢筋。其中下半部分墙体结构长400 cm,高130 cm,宽80 cm,为本次试验对象。

图6 钢筋混凝土墙结构图Fig.6 Structural drawing of the reinforced concrete wall
试验时将EFP装药置于木质支撑架上,装药中心距地面高50 cm,如图7所示。药型罩口部垂直正对混凝土墙,保证EFP垂直侵入墙体内部。试验中炸高设置为30 cm、45 cm,分别为 2.50倍和3.75倍的装药直径。试验过程中,距混凝土墙侧面20 m处架设高速摄像机,记录EFP装药爆炸以及侵彻混凝土墙的过程。试验设置校准完毕后,使用制式电雷管起爆EFP装药。
2.2 试验结果及分析
高速摄像机记录混凝土墙在EFP聚能装药作用下的毁伤过程,如图8所示。以装药起爆时刻作为0时刻点,装药爆炸后,发出巨大的火焰和强光,由于强光、火焰和墙体崩落烟尘的影响,墙体正面混凝土碎块的崩落并不能直接从高速摄像机记录照片中观察到。试验结束后在墙体背面没有观察到明显破坏,但是从高速摄像机记录照片看到,墙体背面在侵彻过程中产生了细微烟尘,这是EFP侵彻过程中墙体内部冲击波向空气中传播引起的。炸高为30 cm时,墙体背面烟尘出现在2.0 ms;炸高为45 cm时,墙体背面烟尘出现在2.8 ms。
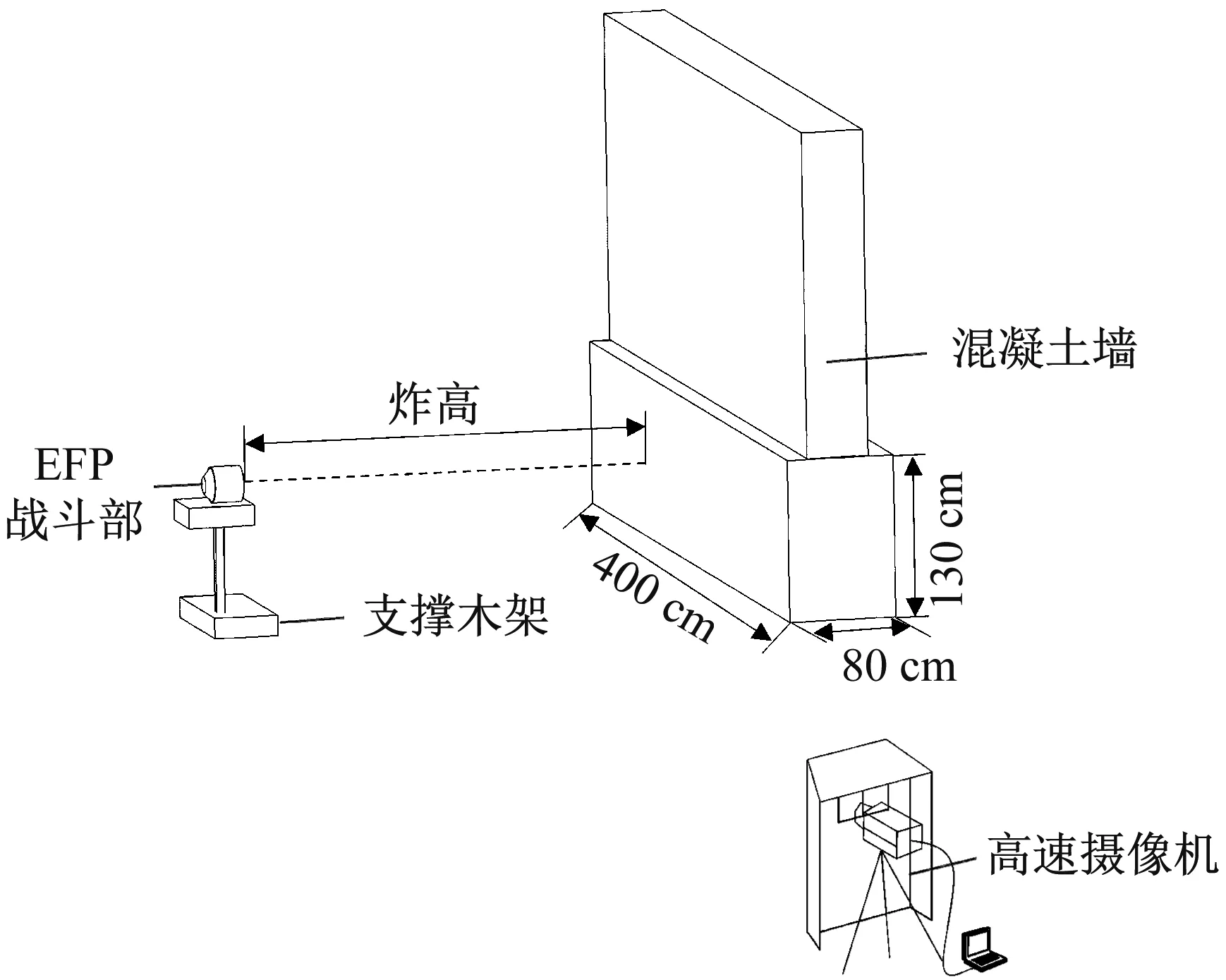
图7 EFP侵彻混凝土墙试验现场布置示意图Fig.7 Schematic diagram of field layout of penetration test

(a) 炸高为30 cm时高速摄像机记录墙体毁伤过程


(a)
图10给出了30 cm炸高下混凝土墙的毁伤情况。可以看到墙体正面严重破损,大量混凝土碎块剥落,形成深度为24.6 cm的漏斗坑,内部壁面比较粗糙,墙体背面没有观察到明显损伤。漏斗坑相对于聚能侵彻体的弹着点基本对称,坑口形状近似为圆形,直径约为 71.0 cm。墙体正面左上角的混凝土碎块因为钢筋的约束并没有完全崩落。由于混凝土墙体尺寸比漏斗坑大得多以及墙内钢筋的约束,漏斗坑以外无明显的裂纹扩展,损伤被限制在局部的范围内。以上结果表明,本次试验墙体可按无限大靶进行分析。
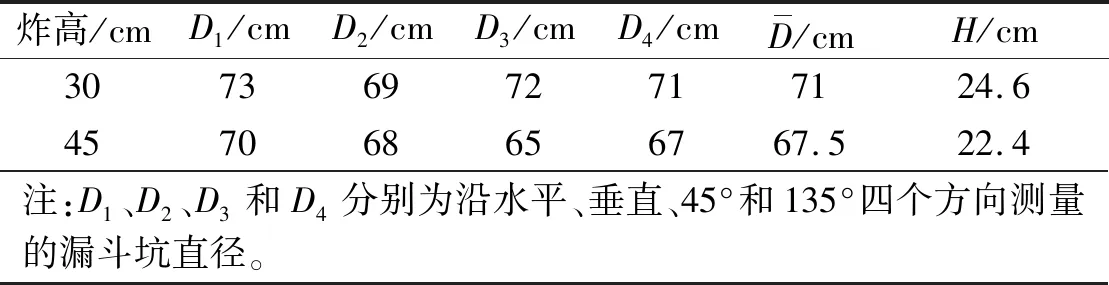
表6 混凝土墙侵彻毁伤试验结果Tab.6 Results of penetration of concrete wall

(a)
如图11所示,炸高增加到45 cm时,墙体破坏情况与炸高30 cm相比无明显变化,墙体正面依旧呈现为一个较大的漏斗坑,墙体背面没有肉眼可见损伤,漏斗坑的直径和深度均略有减小,此时漏斗坑深度为22.4 cm,直径约为67.5 cm。

(a)
观察漏斗坑的内部毁伤情况可以看到,不同炸高下混凝土墙内部第一层钢筋均被EFP打断,出现剪切断裂并向内侧弯曲。周围其他钢筋由于受到冲击、压缩和拉伸等复杂作用,同样存在弯曲变形,断裂钢筋均位于漏斗坑的中心位置处。
3 侵彻混凝土墙的数值仿真
3.1 侵彻数值仿真模型
本文研究球缺型EFP装药近炸对大尺寸混凝土墙的毁伤,关注的重点是漏斗坑直径和深度,需要考虑聚能侵彻体的侵彻破坏以及爆炸冲击波的毁伤效应,因此数值建模时构建了较大范围的空气域。如果采用三维建模仿真,常规工作站根本无法支撑此计算量或将导致计算时间太过漫长,以致没有实际意义。
已有研究结果表明,混凝土靶内部钢筋对聚能侵彻体的侵彻深度影响较小[16],并且当聚能侵彻体的初速大于1 800 m/s时,在钢筋混凝土靶板中可以获得理想侵彻深度[17]。另外一些研究指出,素混凝土的破碎脱落现象与钢筋混凝土靶相比略微明显[18],用素混凝土靶板来代替钢筋混凝土靶板[19],或者通过复合材料理论确定钢筋混凝土的等效弹性模量和等效屈服强度,可以近似代替钢筋在侵彻过程中的作用[20]。鉴于此并考虑到本文试验混凝土墙内部钢筋的横向和纵向间距较大,墙体内部整体配筋率不高,可以认为墙体内部钢筋对毁伤结果影响有限,数值仿真建模时可以忽略钢筋。基于以上分析,本文采用二维轴对称建模进行仿真分析。
如图12所示,在前文EFP成型数值仿真模型的基础上添加混凝土墙模型。混凝土墙采用Lagrange网格建模,药型罩、炸药、空气和混凝土墙之间的相互作用采用流固耦合算法。模型中,EFP侵彻路径上的空气和混凝土墙采用局部网格加密的方法,单元尺寸均为1 mm,侵彻路径以外区域的空气和混凝土墙的网格尺寸均为2 mm。

图12 EFP装药毁伤混凝土墙的数值仿真模型Fig.12 Numerical simulation model of EFP penetrating the concrete wall
3.2 混凝土材料模型及参数确定
混凝土采用MAT_RHT模型描述,该模型是由Riedel等[21]在HJC模型的基础上加以改进得到的,引入偏应力张量第三不变量对破坏面的影响。LS-DYNA程序中的RHT模型可以仅输入混凝土的抗压强度,而后模型内置的参数生成算法将在抗压强度为35 MPa和140 MPa的标准参数集之间进行插值,根据输入的抗压强度数值,自动生成剩余参数。

(1)
(2)
Af=1.6×(35/fcu)1/2
(3)
RHT模型损伤参数D1和D2主要控制累积损坏的速率,其中参数D1主要控制压缩状态下峰值强度后软化分支的形状,Hu等[27]对此进行修正,分别建议采用0.020和0.015。本文通过多次试算,发现D1由默认值0.040调整为0.020、D2保持默认值1.000时的仿真结果与试验结果更加吻合,这与Hu等得出的结论相一致。
经过上述参数修正后,混凝土材料的RHT模型参数取值如表7所示。

表7 混凝土材料参数Tab.7 Material parameters of concrete
3.3 侵彻试验的数值仿真
分别使用修正参数和默认参数的RHT 模型对试验工况进行数值仿真,结果对比如图13和图14所示,图中计算结果为靶体材料损伤分布云图。本文采用Nyström等[28]测量RHT模型预测漏斗坑直径D和深度H的建议,认为数值仿真结果中完全损伤的区域将发生抛掷或剥落,该区域即对应试验结果的漏斗坑,对应于图13和图14中损伤范围为0.99~1.00的区域。
如表8和表9所示,炸高为30 cm和45 cm时默认参数的RHT模型预测漏斗坑直径分别为56.2 cm和54.7 cm,远远小于试验结果的71.0 cm和67.5 cm,漏斗坑直径被严重低估。与预测漏斗坑直径相反,默认参数的RHT模型严重高估漏斗坑深度,预测结果分别为30.1 cm和32.1 cm,明显大于试验结果的24.6 cm和22.4 cm。当采用修正参数的RHT模型时,仿真结果整体明显改善。修正参数的RHT模型预测漏斗坑直径分别为77.0 cm和73.8 cm,预测漏斗坑深度分别为25.8 cm和24.6 cm,数值仿真结果与试验结果吻合较好,最大误差为9.8%。

(a)

(a)
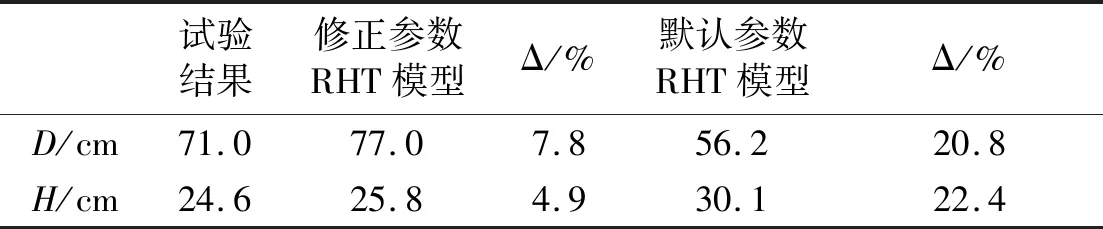
表8 30 cm炸高下修正参数、默认参数的RHT模型的仿真结果与试验结果对比Tab.8 Comparison between simulation results and test results of RHT model with modified parameters and default parameters when standoff distance is 30 cm
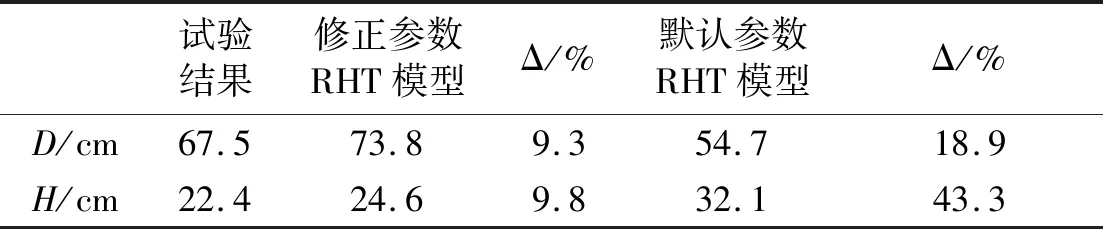
表9 45 cm炸高下修正参数、默认参数的RHT模型的仿真结果与试验结果对比Tab.9 Comparison between simulation results and test results of RHT model with modified parameters and default parameters when standoff distance is 45 cm
如图10和图11所示,试验所用混凝土墙内部钢筋的横向和纵向间距较大,墙体内部整体配筋率不高,但是仍存在一定的约束作用,因此修正参数的RHT模型预测漏斗坑直径均大于试验结果,误差分别为7.8%和9.3%,在可以接受的范围之内。这表明修正参数的RHT模型表现良好,本文建立的数值计算模型对于漏斗坑直径和深度的预测合理可信,可以基于以上数值仿真模型开展进一步的研究。
4 EFP对混凝土墙的毁伤性能
4.1 炸高影响
基于上述已经验证的数值模型和材料参数,进一步开展不同炸高下的数值仿真,研究炸高对于漏斗坑直径和深度的影响,仿真结果如表10所示。表10中:D1为漏斗坑直径;D2为装药直径;H1为漏斗坑深度;H2为炸高;H2/D2为炸高与装药直径比。

表10 不同炸高下漏斗坑直径和深度变化Tab.10 Variation of diameter and depth of funnel pit under different standoff distances
如图15所示,对于本文装药直径为120 mm的球缺型EFP,当炸高在20 cm(1.67倍装药直径)~60 cm(5.00倍装药直径)范围内变化时,随着炸高的增大,漏斗坑直径逐渐由82.0 cm减小至70.6 cm。漏斗坑深度随炸高的变化较为复杂,总体呈先减小再增大再减小的趋势:当炸高由20 cm增加至40 cm(3.33倍装药直径)时,漏斗坑深度由27.6 cm先减小至25.8 cm,而后增大至最大的27.8 cm;当炸高由40 cm增加至60 cm时,漏斗坑深度呈减小趋势并趋于稳定,由27.8 cm减小至最小的24.1 cm。总体上,炸高40 cm时的漏斗坑深度最大,炸高60 cm时的漏斗坑深度最小。
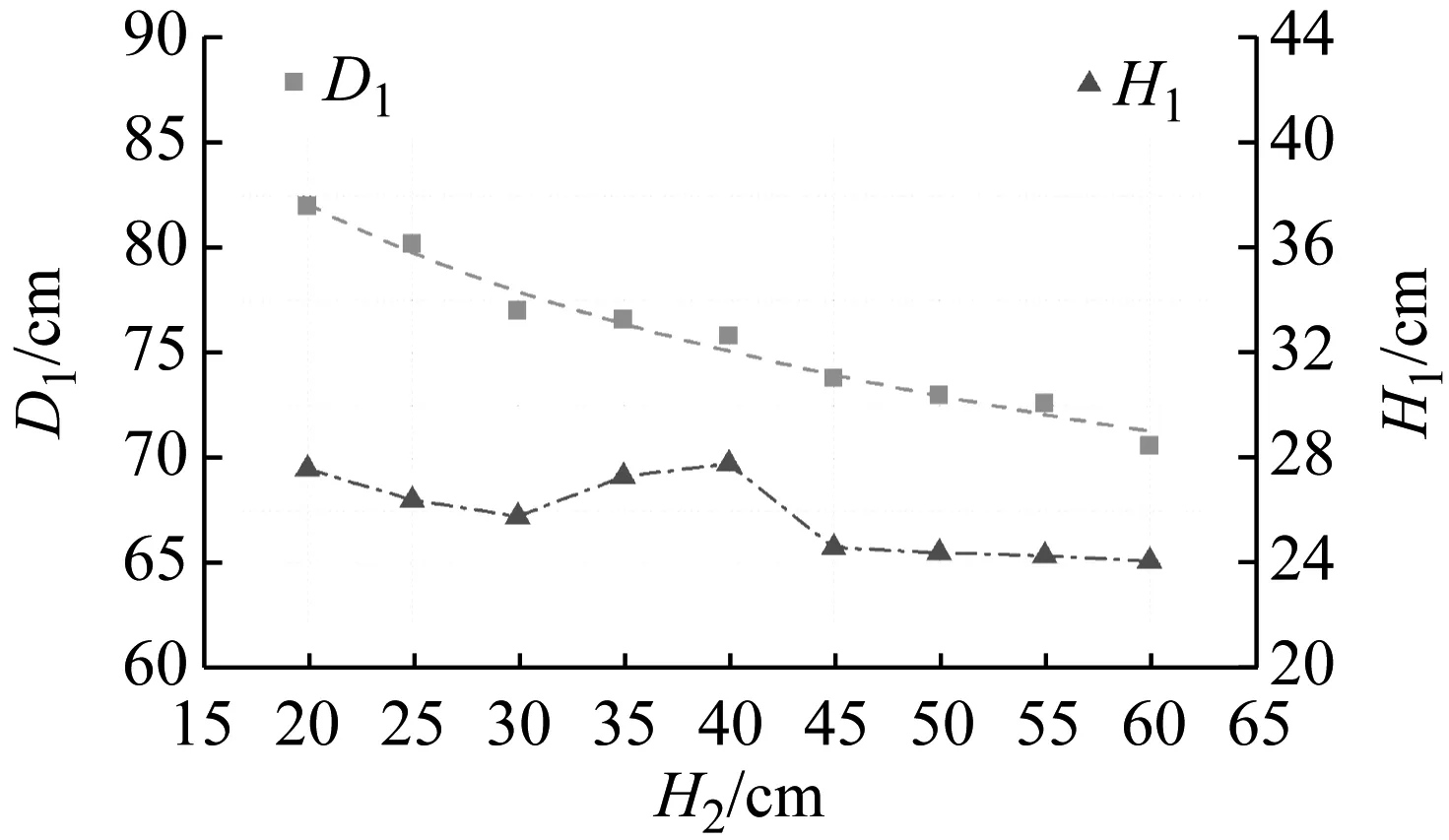
图15 漏斗坑直径和深度随炸高变化Fig.15 Diameter and depth of funnel pit with standoff distances
在侵彻能力方面,通过数值仿真可以发现,对于漏斗坑深度而言,本文设计的Φ120 mm球缺型EFP装药的最佳炸高为40 cm(3.33倍装药直径),此时漏斗坑深度最大。如果综合考虑漏斗坑直径和深度,该EFP装药的最佳炸高为20 cm(1.67倍装药直径),此时漏斗坑直径和深度均较大。下面对此进行分析。
4.2 冲击波与侵彻的联合毁伤效应
前已述及,在近炸作用下EFP装药的爆炸冲击波可对靶体毁伤产生影响。对图12所示的数值模型进行修改,将EFP侵彻作用和爆炸冲击波毁伤作用分开进行研究。为剔除爆轰冲击波的影响仅分析EFP侵彻造成的混凝土墙损伤,建立如图16所示的模型,采取减小空气域的方法进行数值仿真。混凝土墙上方的空气域用于EFP稳定成型,其余空气域用于EFP侵彻混凝土墙的流固耦合作用。
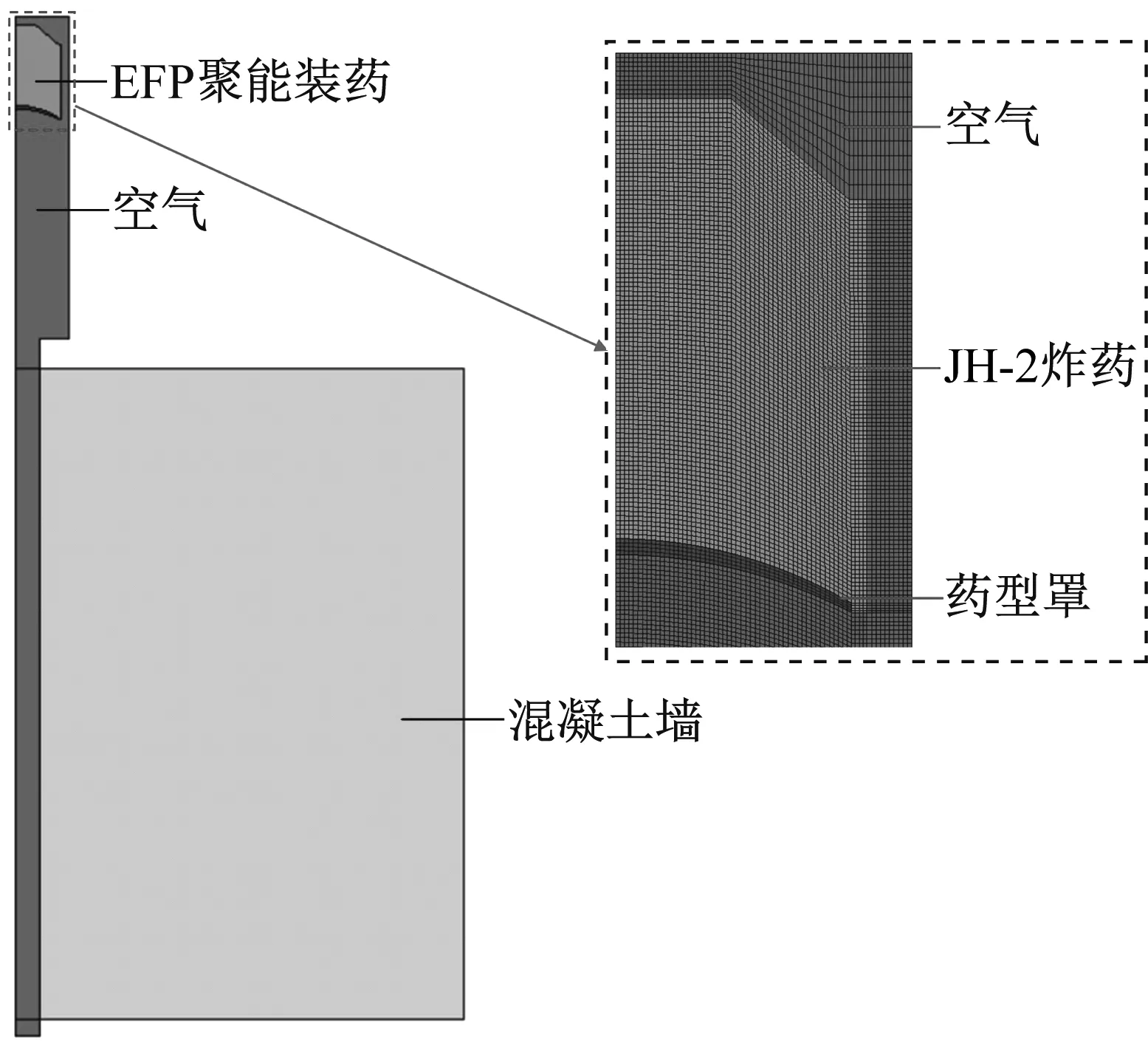
图16 减小空气域后EFP侵彻混凝土墙的数值仿真模型Fig.16 Numerical simulation model of EFP penetrating concrete wall after reducing the range of air
图17显示的是炸高为30 cm并减小空气域后EFP侵彻毁伤混凝土墙的仿真结果。此时漏斗坑直径为54.4 cm,深度为23.4 cm,前文考虑EFP侵彻和爆轰冲击波耦合作用下的漏斗坑直径和深度分别为77.0 cm和25.8 cm。这表明,仅考虑EFP侵彻作用时,漏斗坑直径减小约30%,深度减小约10%。由此分析,爆炸冲击波对漏斗坑直径影响较大,漏斗坑深度主要是由EFP侵彻造成的,但是在与EFP侵彻的耦合作用下,爆轰冲击波能够一定程度上提高漏斗坑深度。

图17 炸高为30 cm并减小空气域时混凝土墙毁伤情况Fig.17 Damage of EFP penetrating the concrete wall when the standoff distance is 30 cm and air area is reduced
为进一步研究EFP侵彻与爆炸冲击波的联合毁伤元作用机理,对EFP毁伤混凝土墙的过程进行详细分析。EFP装药毁伤混凝土墙的压力云图,如图18所示。t=1 μs时,主装药在顶部起爆点起爆,随后爆轰波在炸药内部传播并引爆剩余炸药。t=11 μs时,炸药爆轰产物和冲击波开始作用于药型罩,药型罩逐渐加速、自锻变形。t=20 μs时,药型罩开始产生明显的整体向前运动,此时药型罩直径较大,阻碍部分爆轰产物和冲击波向前传播,外围爆轰产物和冲击波经过绕射传播至药型罩前方并继续向前传播。t为20~96 μs时,由于爆炸冲击波传播速度大于EFP飞行速度,因此爆炸冲击波前沿始终位于EFP的前方。随着传播距离的增大,爆炸冲击波强度逐渐减弱。t=96 μs时,爆炸冲击波开始作用于混凝土墙,入射冲击波强度为7.3 MPa,墙体表面反射压力达到43.3 MPa,此时EFP头部距混凝土墙仍有5.8 cm。随后,爆炸冲击波产生的应力波将首先在墙体内部进行传播,并先于EFP对墙内局部区域产生损伤,这将有利于EFP侵彻作用的发挥,最终将在一定程度上提高漏斗坑深度。t=115 μs时,EFP开始侵彻混凝土墙,在侵彻过程中,EFP头部将持续产生高压冲击波并向墙体内部传播。EFP侵彻将造成墙体局部区域的粉碎性破坏并扩大其内部裂纹区,裂纹区的范围及裂纹分布主要取决于墙体内部应力波的传播,能够有效降低混凝土的抗压和抗拉性能。t>115 μs时,外围爆炸冲击波逐渐传播至混凝土墙表面,并与EFP持续侵彻在墙体自由表面反射形成拉伸波相互叠加,产生的拉应力超过混凝土的抗拉强度,造成混凝土墙的局部崩落。

图18 EFP毁伤混凝土墙作用过程的压力云图Fig.18 Pressure cloud image of EFP penetrating concrete wall
上述结果表明,近炸作用下EFP侵彻和爆炸冲击波耦合会对漏斗坑形成产生影响,但影响过程较为复杂。从前面的分析首先可以看到,炸高在20~60 cm范围内变化时,随着炸高增大爆炸冲击波强度和传播速度均逐渐衰减,炸高为20 cm时入射冲击波强度可达13.8 MPa。随着炸高增加,EFP与冲击波到达墙体的时间间隔逐渐减小,炸高为60 cm时,EFP已经追赶上爆炸冲击波前沿,先于爆炸冲击波对墙体进行侵彻作用,此时漏斗坑直径逐渐减小。另一方面,不同炸高下EFP着靶时的成型状态区别很大,见表5。炸高为20~40 cm时,随着炸高增大,EFP头尾速度和长径比均在快速变化,EFP侵彻性能随之发生改变,同时爆炸冲击波强度逐渐减弱,此时漏斗坑深度先减小后增大。炸高为45~60 cm时,随着炸高增大,EFP成型基本稳定,侵彻性能变化较小,爆炸冲击波强度逐渐减弱,相应EFP侵彻和爆炸冲击波的联合毁伤效应减小,漏斗坑深度逐渐减小并趋于稳定。
5 结 论
本文开展不同炸高下球缺型EFP聚能装药毁伤大尺寸混凝土墙试验,基于修正参数的RHT模型进行数值仿真,分析炸高对漏斗坑直径和深度的影响规律,研究EFP高速侵彻破坏与爆炸冲击波对混凝土墙的耦合作用过程,探讨漏斗坑毁伤机理,得到以下研究结论:
(1) 本文设计的Φ120 mm球缺型EFP聚能装药非常有效,在比较大的炸高范围内均能够获得稳定、连续的EFP聚能体。炸高为15 cm(1.25倍装药直径)~70 cm(5.83倍装药直径)时,头部速度、头尾速度差随炸高增大而逐渐减小,尾部速度、长径比随炸高增大而逐渐增大,以上变化趋势均随炸高增大而逐渐减小并最后趋于稳定。
(2) 炸高为20~60 cm时,随着炸高增大,漏斗坑直径逐渐减小。炸高为20 cm(1.67倍装药直径)~40 cm(3.33倍装药直径)时,漏斗坑深度随炸高增大而先减小后增大,炸高为40 cm时漏斗坑深度最大;炸高为40~60 cm(5.00倍装药直径)时,漏斗坑深度随炸高增大而呈现减小趋势并趋于稳定。综合考虑漏斗坑直径和深度,本文研究工况中最佳炸高为20 cm,此时漏斗坑直径为6.83倍装药直径,漏斗坑深度为2.30倍装药直径。
(3) 不同炸高下,EFP聚能体和爆炸冲击波对混凝土墙进行作用的先后顺序不同。小炸高下,爆炸冲击波先于EFP聚能体到达混凝土墙。随着炸高增大,EFP聚能体将逐渐追赶上爆炸冲击波,先于爆炸冲击波到达混凝土墙。但是通过仿真结果分析,爆炸冲击波对混凝土墙毁伤作用有限,漏斗坑主要由EFP侵彻作用所产生。
(4) 基于修正参数的RHT模型开展侵彻数值仿真,仿真结果能够准确预测混凝土墙的漏斗坑直径和深度,与试验结果吻合较好,最大相对误差为9.8%。

