基于贝叶斯优化BiLSTM模型的输电塔损伤识别

魏佳恒，郭惠勇

(重庆大学 土木工程学院，重庆 400045)

特高压输电塔穿越高海拔地区，所处环境复杂、恶劣，由于其结构高耸、刚度弱的特点，在长期服役期间易产生结构损伤[1]。因此对输电塔结构进行运行状态监测和损伤识别至关重要。结构健康监测系统在运营期间会积累海量监测数据，基于大数据及深度学习思想的结构健康监测研究是当前该领域的研究热点[2-3]。

深度学习具备精度高、鲁棒性强和抗噪能力强等优点，利用大量数据对多层网络模型进行训练以得到精确、足够的特征信息,而不受传统神经网络的限制[4]。目前深度学习已广泛运用于各领域的研究，其中在结构损伤识别领域主要是基于结构振动响应的方法，利用损伤结构的振动响应信号提取损伤特征，并以此建立信号与结构损伤状态的映射关系[5]。由于循环神经网络(recurren neural network，RNN)和长短时记忆神经网络(long and short-term memory，LSTM)对于处理时间序列数据具有明显优势，目前已有不少运用于机械故障诊断领域的研究。Talebi等[6]运用角速度作为的输入向量，建立了某风能转换结构的故障监测系统，研究发现该方法在短期监测中具有较好的检测能力；赵志宏等[7]等提出一种基于双向长短时记忆网络模型BiLSTM的故障诊断的方法，将机器原始振动信号作为模型输入向量,训练提取不同故障类型的故障特征，结果验证了该方法的有效性；杜小磊等[8]将深层小波卷积自编码分析与长短时记忆网络相结合运用于轴承故障诊断之中，结果表明该方法提取特征和识别故障能力优于人工神经网络、支持向量机等传统方法；Cabrera等[9]将贝叶斯方法与LSTM模型相结合，提出一种压缩机的故障检测方法，结果故障识别的准确率达到93%以上。

超参数选取也是目前深度学习面临的较为棘手的问题，模型超参数组合与网络模型性能密切相关。贝叶斯优化是一种十分有效的全局优化算法，其目标是找到优化问题的全局最优解[10]。目前，已有贝叶斯优化运用于各类模型参数优选的研究，如Zhong等[11]提出通过应用贝叶斯优化搜索支持向量机模型的C和γ超参数，用于工业测量数据分类。Wang等[12]提出了贝叶斯优化结合粒子滤波的轴承故障特征提取方法等。

损伤结构的加速度响应数据是时间序列数据，可以反映结构的状态信息，蕴含结构的损伤特征，通过BiLSTM模型可以有效提取其中特征，解决损伤识别的问题。在输电塔的健康监测中，可以较为容易地测得结构的加速度响应序列，而双向长短时记忆网络可以有效地处理加速度响应数据，故本文采用了BiLSTM模型进行输电塔的损伤识别研究，并采用贝叶斯优化选取模型的超参数组合，通过输电塔仿真模拟和试验研究验证了该方法的有效性，并且相对其他模型具有更好的损伤识别效果。

1 BiLSTM模型

LSTM由RNN神经网络演变而来，在传统RNN神经网络输入层、隐藏层和输出层的结构基础上，改进了隐藏层的结构。通过引入门机制来控制信息传递的路径，并通过门对经过网络的信息进行有选择的记忆或删除[13]。

it=σ(Wixt+Uiht-1+bi)

(1)

ft=σ(Wfxt+Uiht-1+bf)

(2)

ot=σ(Woxt+Uoht-1+bo)

(3)

(4)

(5)

ht=ot⊗tanh(Ct)

(6)

式中:Wi、Wf和Wo表示从输入门、遗忘门和输出门到下一个输入门的权重矩阵；Ui、Uf和Uo表示隐含层的权重矩阵；bi、bf和bo分别表示各个门结构的偏置矩阵。σ为Sigmoid激活函数。

图1 LSTM结构示意图Fig.1 The structure of LSTM

(7)

(8)

(9)

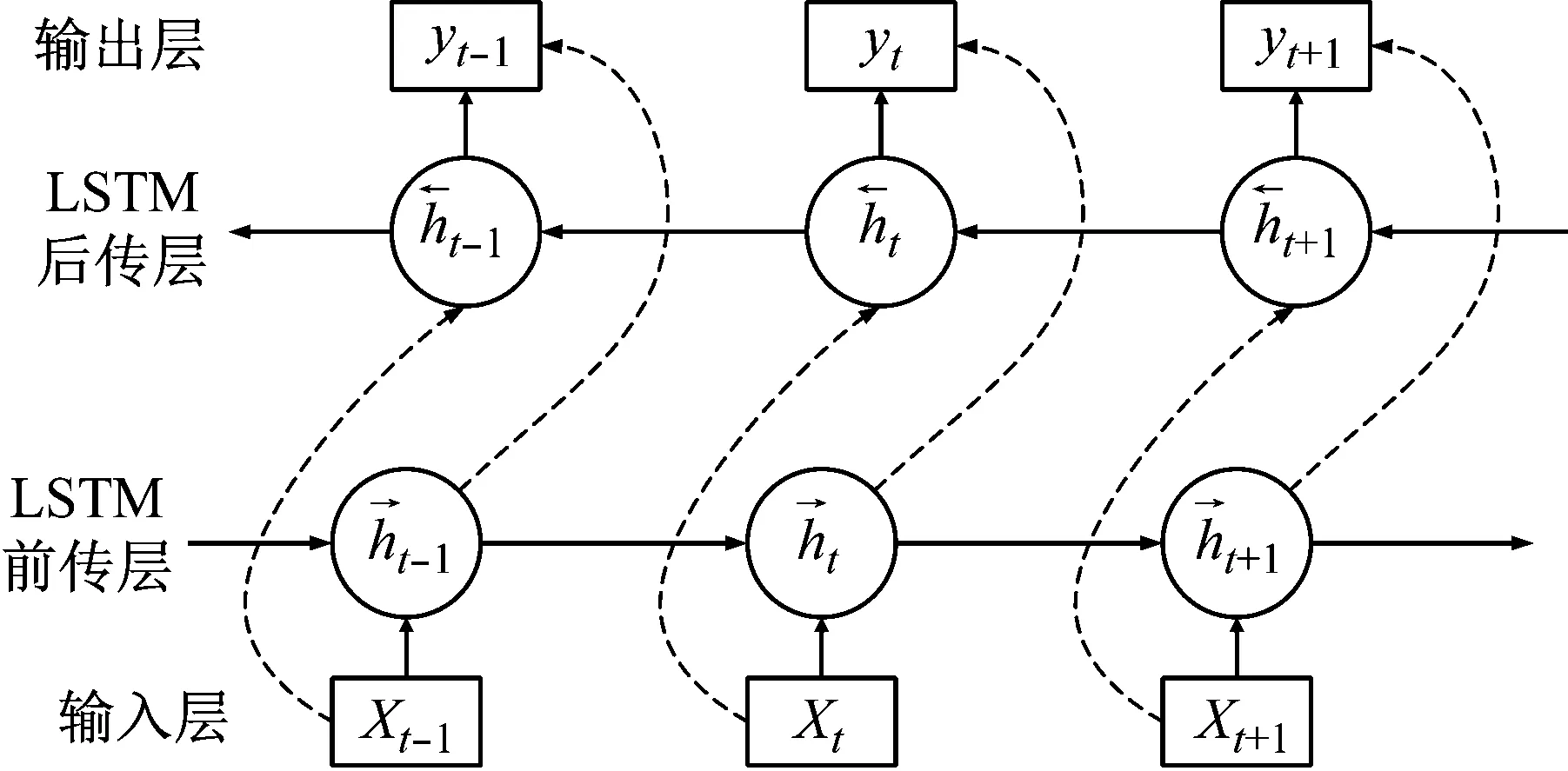
图2 BiLSTM结构示意图Fig.2 The structure of BiLSTM

2 贝叶斯优化的BiLSTM模型

2.1 贝叶斯优化

应用BiLSTM模型进行损伤识别时，需要确定模型最优超参数组合。构造一种优秀的算法需要大量参数调节试验，耗时耗力也不一定取得好效果。本文引入一种全局优化算法——贝叶斯优化(Bayesian optimization，BO)选取模型超参数组合。贝叶斯优化基于贝叶斯定理，运用概率代理模型拟合真实目标函数，并根据拟合的结果选择接下来最有可能的点进行评估，利用历史信息合理减少评估次数，提高搜索效率。

贝叶斯优化的框架主要包含两个核心部分：概率代理模型和采集函数。概率代理模型包含先验概率模型和观测模型；采集函数是根据后验概率分布构造的函数[16]，选用合适的概率代理模型和采集函数才能获得更好的优化效果。

2.1.1 概率代理模型

概率代理模型通常分为参数模型与非参数模型，非参数模型更为灵活，且不易发生“过拟合”，其中以高斯过程(Gaussian process,GP)应用最为广泛[17]。

高斯过程是多元高斯概率分布的泛化[18],由一个均值函数m和一个协方差函数k构成。在高斯过程中，有限个随机变量都满足一个高斯联合分布。首先假设一个均值为0的先验分布

p(f|X,θ)=N(0,Σ)

(10)

式中：X为训练集;f为未知函数f函数值的集合;Σ为k(x,x′)构成的协方差矩阵;θ为超参数。

假设存在的噪声ε满足独立同分布的高斯分布:p(ε)=N(0,σ2),则似然分布为

p(y|f)=N(f,σ2I)

(11)

式中,y=f(x)+ε，y表示观测值y的集合。

可得边际似然分布为

p(y|X,θ)=N(0,Σ+σ2I)

(12)

因此，存在联合分布为

(13)

p(f*|X,y,X*)=N(〈f*〉,cov(f*))

(14)

(15)

(16)

式中：〈f*〉表示预测均值；cov(f*)是预测协方差。

2.1.2 采集函数

在贝叶斯优化中,采集函数是用来选择下一个最有可能的模型最佳性能评估点的方法。该函数通过已经观测到的数据集D1:t，得到后验分布构造，并通过对其最大化来指导下一个评估点xt+1。期望提升(expected improvement,EI)的参数少且具有整合提升的概率，平衡深度和宽度的关系的优点，故本文采用EI作为采集函数，其具体公式如下

αt(x,D1:t)=

(17)

式中:v*为当前最优函数值;φ为标准正态分布概率密度函数。

2.2 贝叶斯优化的BiLSTM模型

利用贝叶斯优化对BiLSTM模型进行超参数选取时，可以考虑成以下公式进行求解

x*=arg minf(x),x∈X

(18)

式中：f(x)为目标函数;x表示一组超参数组合;X表示超参数组合空间;x*则表示X中的一组x，使目标函数f(x)取得最优解。本文以BiLSTM模型识别损伤的误差率valError作为贝叶斯优化的评价函数f(x),公式如下所示

(19)

式中：N为所有待检测样本组数；R为N组样本数据中所预测损伤类型与真实损伤类型相一致的样本组数。

本文采用高斯过程代理超参数组合x到BiLSTM模型的函数关系，根据已观测的数据集得到后验分布构造，然后通过EI函数选取下一个评估点，迭代修正先验信息，逐步提高代理模型准确性，寻找使目标函数取得最优解的超参数组合。

BiLSTM模型超参数众多，本文重点选取其中两个超参数(初始学习率、小批量尺寸)进行优化选取。根据BiLSTM反向传播传播算法可知，其权重更新公式为

(20)

式中：α为学习率；n为小批量尺寸。由式(20)可知，除了梯度本身，学习率和小批量尺寸直接决定模型的权重更新，从优化本身来看都是影响性能收敛最重要的参数。小批量尺寸决定模型每次参数更新损失函数的数据量，而学习率决定了权重迭代的步长。对于不同的数据与模型，其最适的学习率和小批量尺寸也不同，没有合适的选取法则，故本文采用贝叶斯优化的方法选取。

2.3 基于贝叶斯优化的BiLSTM模型损伤识别方法

2.3.1 模型执行步骤

运用BO-BiLSTM模型进行损伤识别的具体步骤如图3所示。

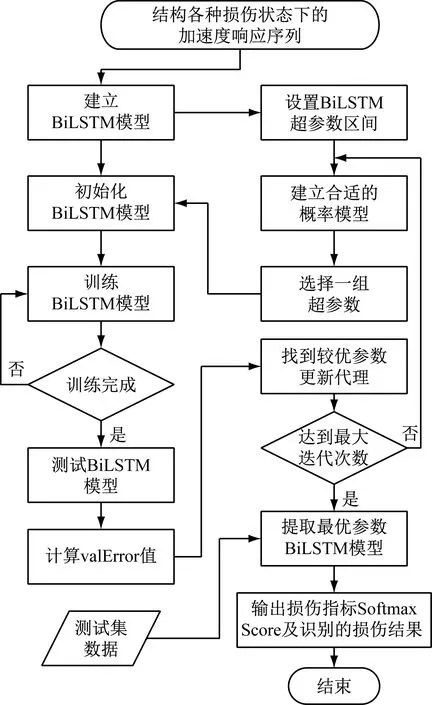
图3 基于贝叶斯优化BiLSTM模型的结构损伤检测流程Fig.3 Structural damage detection process based on BO- BiLSTM model

步骤1首先获取不同损伤工况下结构每一层的加速度数据，可以通过模型试验或者数值模拟获得，使用z-score函数对数据标准化处理，建立样本数据集，划分训练集、测试集和验证集。

步骤2建立BiLSTM模型，确定网络模型的超参数，并设置需要优化的超参数(初始学习率、小批量尺寸)区间。

步骤3进行贝叶斯优化，以BiLSTM网络模型作为优化的目标函数，以valError值作为评价函数，使其到达最小值。

步骤4在当前超参数组合下，以训练集和验证集训练BiLSTM模型，计算当前超参数下模型评价函数的值，完成后返回贝叶斯优化，根据概率模型采集函数选取下一组超参数进行新一轮训练，直至到达迭代次数。

步骤5输出贝叶斯优化后模型性能最优一组超参数及其BO-BiLSTM网络模型。

步骤6此时BO-BiLSTM模型已经具备损伤检测能力，将测试集数据输入模型，输出损伤状态，同时输出网络Softmax-score，验证模型性能。

2.3.2 损伤评价指标

BO-BiLSTM模型进行机械故障诊断或结构损伤识别，从本质上来说是一个多分类的问题。对于每一个待检测的损伤数据样本，通过网络模型后可以得到一个N维数组作为输出结果。数组中的每一个维度对应一个结构损伤类别，通过前向传播算法得到输出层的输出纬度值代表属于这个结构损伤类别的可能性大小。Softmax回归可以将神经网络的前向传播输出的数值分布转化为概率分布，使每个样本分类到不同损伤类别的概率和为1。

(21)

如式(21)所示，BO-BiLSTM模型原始输出层的输出值被作为置信度通过softmax层来生成新的输出，该输出满足概率分布的所有要求。因此，使用softmax层输出的各类损伤工况概率值Softmax-score作为本文方法中验证网络损伤识别效果的评判指标。

3 输电塔有限元模型损伤识别仿真

3.1 输电塔有限元模型

为验证本文提出的BO-BiLSTM模型的有效性，通过ABAQUS软件对一个小型的干字型输电铁塔进行有限元模拟，以高斯白噪声作为底部激励获取结构在不同损伤工况下的加速度响应数据，并以此训练网络模型，计算其损伤识别的准确率。

该模型采用梁单元建模，建立的输电塔模型及其尺寸详细信息如图4和图5所示，输电塔的主材、横隔件以及横担采用钢材，其斜材和交叉斜撑采用铝材，具体材料与截面信息如表1所示。将输电塔按分为8层子结构，损伤杆件的刚度折减系数设置为0.95，采用损伤不同杆件数量的方法模拟不同程度损伤工况，损伤工况如表2所示。本文基于Matlab2019b建立BO-BiLSTM模型，采用BiLSTM模型,BO-LSTM模型作为对比方法，验证其优越性。

图4 输电塔有限元模型Fig.4 The finite element model of transmission tower

图5 输电塔模型尺寸平面图Fig.5 Dimension plane of transmission tower model

表1 构件材料信息表Tab.1 The information of component material

表2 损伤工况信息表Tab.2 The information of damage conditions

3.2 数据集构建

本文研究其横担构造之下的5层子结构损伤识别情况。每种工况取如图5所示6个测点的加速度响应数据作为构造特征的原始数据，在不同白噪声激励下进行10次模拟，每次白噪声激励时长为25 s，取样频率为1 000 Hz，单一工况数据集长度为250 000×6。共得到5种损伤位置(1-5层)，2种不同损伤程度(损伤2杆和损伤4杆)的11种工况的数据，将每种工况数据划分为6×500的矩阵样本，即每个样本采样时间为0.5 s，每种工况500个样本。采用z-score方法对数据进行标准化，11个工况共5 500个样本。取整个数据集的前60%并打乱顺序作为网络的训练集；取后20%作为贝叶斯优化的验证集，验证贝叶斯优化效果；最后取数据集剩余20%作为模型的测试集，测试模型损伤识别效果，且防止模型对部分数据过拟合，测试模型的泛化能力。

3.3 BiLSTM模型架构

BiLSTM损伤识别模型架构如图6所示，网络模型共分为5层，包含1个输入层，1个BiLSTM隐含层，1个全连接层，1个softmax层以及1个分类输出层。输入数据首先进入BiLSTM神经单元中进行计算，将其输出值作为全连接层的输入，计算后输出值作为softmax层输入值，输出样本数据分类至每种工况的概率分布，最后由分类输出层输出样本对应的损伤工况。

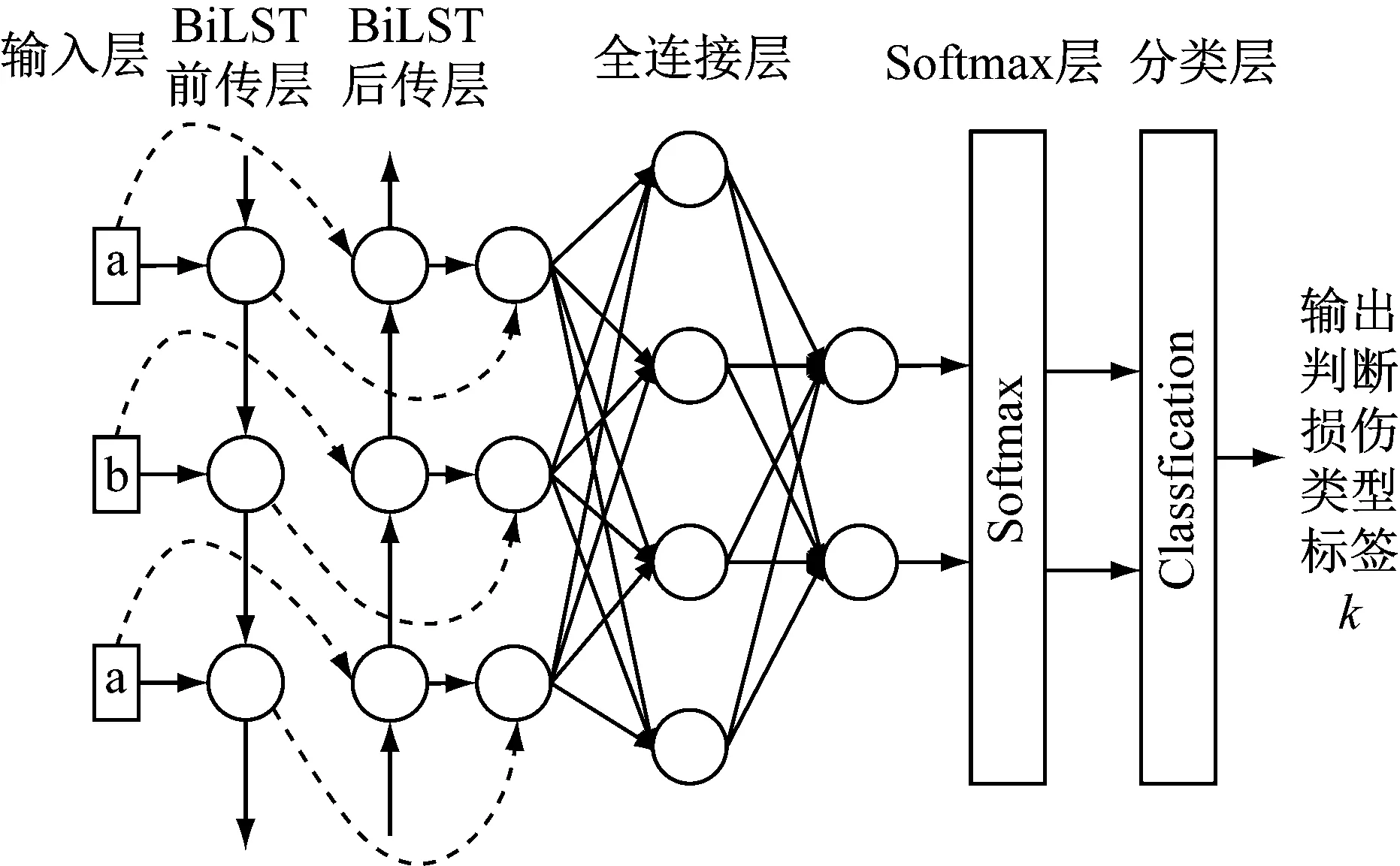
图6 BiLSTM损伤识别模型架构图Fig.6 The structure of BiLSTM damage identification model

根据输电塔有限元模型结构实际情况以及所采集的加速度响应数据，对三个重要超参数(初始学习率、小批量尺寸、L2正则化系数)设置优化区间，其他超参数依据调参经验进行设置，具体参数设置如表3所示。

表3 BiLSTM参数设置Tab.3 BiLSTM parameter settings

对BiLSTM模型进行贝叶斯优化，迭代次数设置为30次，达到计算次数后停止优化，输出最优超参数组合。寻优过程如图7所示，优化至第30次迭代时模型性能达到最优，超参数组合为InitalLearnRate=0.014 511,MiniBatchsize=255，即模型在经过贝叶斯优化选取不同超参数组合后，BiLSTM模型整体识别准确率由63.9%提升至92.9%。使用测试集数据对BO-BiLSTM模型进行验证，结果发现该模型对测试集样本损伤识别准确率为94.20%，相对验证集提高1.34%，表明BO-BiLSTM模型具有很好的数据泛化能力，具备损伤识别能力。

图7 贝叶斯优化寻优过程Fig.7 Bayesian optimization process

3.4 损伤识别结果分析

使用测试集1 100个样本对上节最优BO-LSTM模型进行损伤识别测试，分别从损伤位置以及损伤程度两方面对模型损伤识别能力进行进一步分析。

3.4.1 损伤位置分析

输电塔有限元试验设置的损伤情况为1～5层每层分别损伤4根杆件和损伤两根杆件，故每层有100×2个测试样本。现将测试集分别经过BiLSTM、BO-LSTM和BO-BiLSTM网络模型识别，各层的识别结果及定位准确率，如表4所示。

表4 数值仿真损伤位置识别准确率Tab.4 Damage location identification accuracy rate of numerical simulation

根据表4结果显示，BO-BiLSTM网络模型对于输电塔有限元模型层间损伤位置定位的整体准确率在94.36%，整体识别效果相对其他两个模型更加稳定:BiLSTM模型对高层损伤识别准确，而对底层损伤识别效果较差；BO-LSTM总体识别效果不错，但是对第四层损伤识别效果不太理想。为进一步分析模型性能，故提取出不同模型每层损伤工况样本Softmax-score均值，其结果如图8所示。

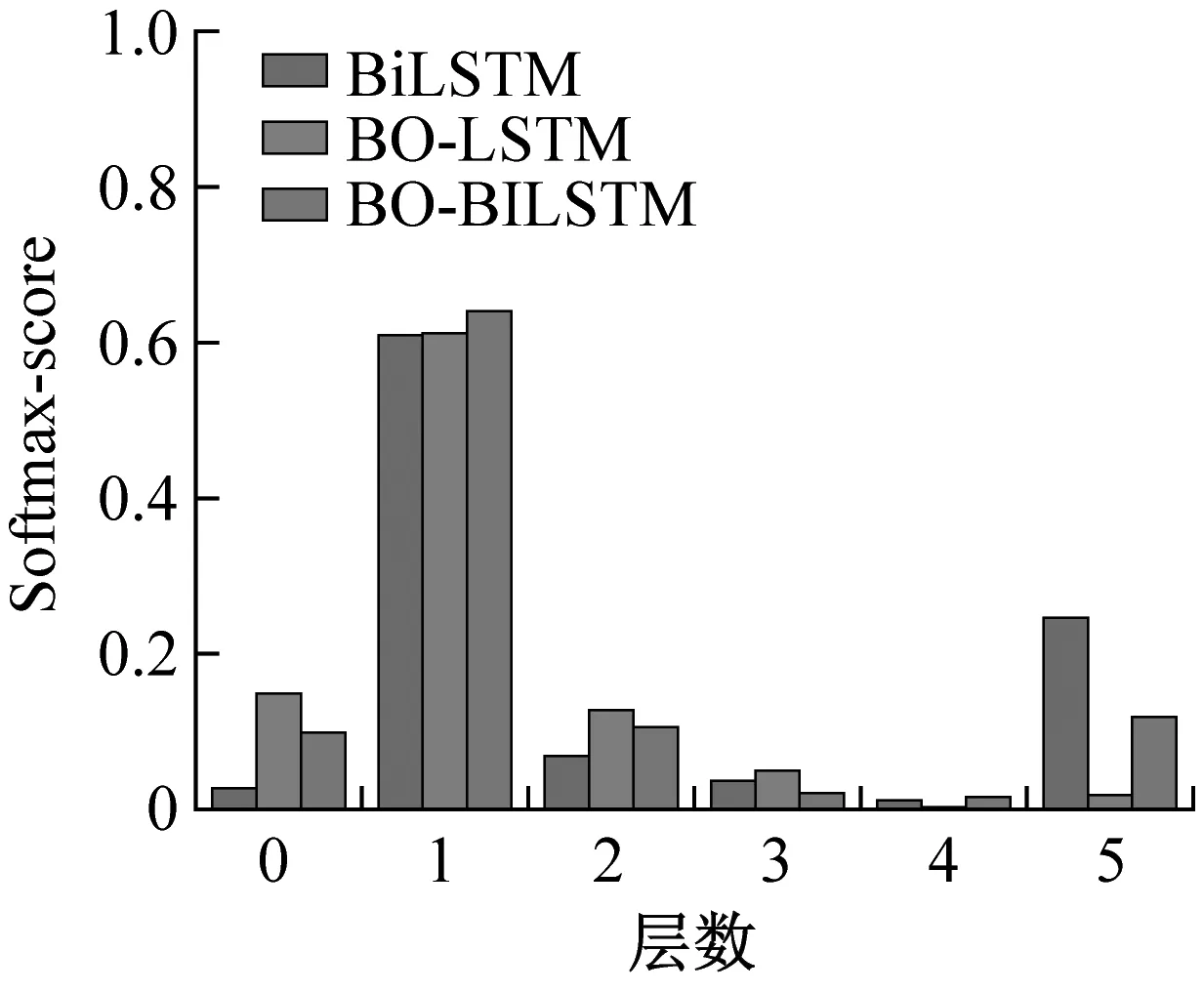
图8 数值仿真损伤位置识别结果Fig.8 Damage location identification results of numerical simulation

Softmax-score反映模型判断待检测样本到各种损伤位置的概率分布。根据图分析可知，各层损伤的Softmax-score值随损伤层数的增加而上升，表明各模型对高层损伤的损伤特征提取更为准确，对高层损伤的定位更为精准。对比不同模型Softmax-score，BO-BiLSTM模型基本处于各模型最高值，而BO-LSTM模型对第4层损伤的识别出现误差，易与第3层损伤产生混淆。综合以上对比结果可知，经过训练后的BO-BiLSTM模型可以准确定位出输电塔模型层间损伤的位置，定位效果相比另两个模型更为稳定。

3.4.2 损伤模式分析

主要考虑了输电塔每层损伤的两种损伤模式，即损伤2根杆件和4根杆件。故五层塔架结构考虑了10种损伤模式，具体如表5所示。该表包含10种损伤模式1～10，而模式0代表无损伤模式。表5还包含各长短时记忆网络模型对不同损伤工况的识别结果与准确率。

由上述结果可以看出，BO-BiLSTM模型可以在定位输电塔层间损伤的基础上，区分相同损伤位置下不同模式的损伤。单层损伤4根杆件模式的识别准确率基本达到100%；损伤2杆模式的准确率有所下降，但也维持在84%以上。同时，随着损伤所在层数的增加，模型对损伤模式识别准确率也随之上升。对比三个模型结果可知，各模型对强损伤模式均保有较高的识别准确率；对于弱损伤模式，BO-BiLSTM模型识别效果更好，未进行贝叶斯优化的BiLSTM模型对低层弱损伤模式失去判断能力，提取特征能力较差。为进一步分析各模型性能，将不同程度模式下Softmax-score提取出来如图9所示，其中模式0表示结构未损伤状态。

表5 数值仿真损伤模式识别准确率Tab.5 Damage pattern identification accuracy rate of numerical simulation

图9 数值仿真损伤模式结果Fig.9 Damage pattern identification results of numerical simulation

整体分析，三种模型对弱损伤模式识别效果相对较差，如模式6(第1层损伤2杆)情况下，模型对该模式损伤判定较为模糊，分类至模式6的概率值仅略微高于其他模式，表明模型对该模式下损伤的特征提取效果不够好，容易出现误判现象；而对强损伤模式的Softmax-score均接近于1，基本都可以准确判别损伤情况。结合识别准确率分析，BO-BiLSTM模型对输电塔模型层间损伤的损伤特征提取更为准确，特别是对小损伤模式识别效果优于另两个模型，经过训练后对输电塔损伤具有良好的诊断能力。

4 输电塔损伤识别试验研究

4.1 试验介绍

为验证本文所提出模型对实际结构的损伤识别效果，本节尝试将有限元模拟与试验相结合，即先通过有限元模型获取结构在各种损伤工况下的加速度响应数据训练BO-BiLSTM模型，再通过试验获取的损伤数据组成测试集，以此测试BO-BiLSTM对实际输电塔结构损伤提取的鲁棒性。本文将以第3章的输电塔有限元模型为例，设计制作输电塔结构试验对本文所提方法进行研究。

输电塔试验模型尺寸与材料均与有限元模型一致，输电塔共分为8层，塔杆总高度为2.6 m；第1～5层高度均为400 mm；第6～8层每层高度均为200 mm，塔身四肢主材为空心钢管，直径为10 mm，所有横隔件为实心圆钢，直径为6 mm；塔身四面斜材以及每层横截面方向上交叉支撑由正方形截面实心铝杆组成。如图10所示，塔身主材每层节点上焊接有空的薄钢片，通过螺栓将斜材、交叉支撑相连接。横担件通过焊接的方法与主材相连接；输电塔的每个柱脚焊接在一个10 mm厚的钢板上，每个钢板通过4颗螺栓与振动台相连接，以确保固定方式为固接。

(a) 试验模型

本次试验利用小型振动台对结构进行加载，在y方向上施加10段随机生成带宽为20～50 Hz的25 s高斯白噪声作为结构的激励。通过东华动态信号测试分析系统以及加速度传感器采集结构第1～5层和第7层的加速度响应数据。加速度传感器的布置位置与有限元模型中所选取的节点保持一致，易于模型的识别匹配。

通过拆除单根或多根塔身斜材来模拟结构层间损伤，而由于铝材轻质的特点，可以减少由于拆除构件后对结构整体质量的影响。本次试验一共设置了六种损伤工况和对应模式，分别考虑第3层、第4层和第5层发生不同程度损伤的情况，损伤工况与有限元模拟对应工况如表6所示。

表6 试验的损伤工况设置Tab.6 States of transmission tower model experiment

为避免振动台刚启动时和即将结束时产生的误差对结果的影响，本文对每个通道获得的加速度数据做截断处理，将试验采集的加速度数据去掉前后，截取中间100 000个数据进行研究。图11是试验工况6下通道1、3、5采集的加速度响应数据节选。将试验每种损伤工况采集的数据划分为6×500的矩阵样本，采用z-score对数据进行标准化构成验证集。

图11 试验工况6下通道1、3、5加速度响应数据节选Fig.11 Part of the accelerations data of the channel 1,3 and 5 at test case 6

4.2 试验结果分析

为验证3.3节训练所得模型对实际结构的损伤识别效果，将试验所得样本直接作为测试集样本输入上节训练完成BO-BiLSTM模型进行损伤识别，整体识别准确率达到了79.6%。下面将具体从损伤位置和损伤程度对结果进行分析。

4.2.1 损伤位置识别分析

现将测试集经过BO-BiLSTM、BiLSTM和BO-LSTM网络模型识别，各层的识别结果及定位准确率,如表7所示，各层Softmax-score如图12所示。

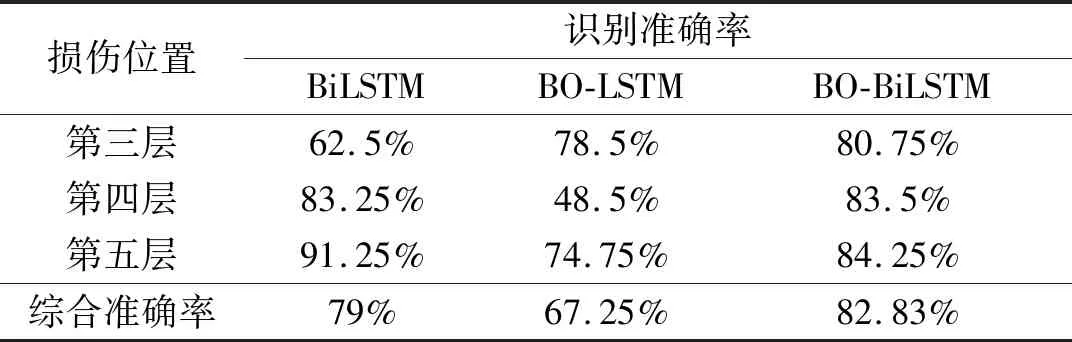
表7 试验损伤位置识别准确率Tab.7 Damage location identification accuracy rate of experiment

根据表7结果显示，使用输电塔试验数据作为测试集，测试通过有限元模拟数据训练出的BO-BiLSTM模型，整体的损伤定位准确率为82.8%，相对有限元结果有所下降，但仍保持有较高准确率。层间损伤的定位准确率从第3层的80.75%逐渐上升至第5层84.5%，准确率随层数的增加而上升。对比三个模型识别结果可以发现，BO-BiLSTM模型整体识别效果更稳定，而BiLSTM和BO-LSTM模型在某些层均出现了较大波动，准确率较低。

分析各模型的Softmax-score可知，各模型对试验层间损伤的定位表现结果与有限元模型结果基本相同，经过贝叶斯优化的BO-BiLSTM模型整体保持较高性能，可以较为准确提取不同位置损伤工况的定位特征；BiLSTM模型则对较低层的损伤特征提取不够明显，识别效果较差；BO-LSTM模型则对第4层损伤特征提取出现较大误差，易与第3层损伤混淆。

图12 试验的损伤位置识别结果Fig.12 Damage location identification results of experiment

4.2.2 损伤模式识别分析

在试验中每层损伤也设置了两种损伤模式，即2杆损伤和4杆损伤。在本文第3章中，输电塔有限元模型的杆件损伤通过刚度折减0.95的方法进行模拟。由于试验条件限制，试验中采取拆除杆件的方法模拟结构的刚度变化，故存在一定误差。试验中设置的2种损伤模式，与有限元模型模拟工况一致。表8所示为三种长短记忆网络模型对不同损伤工况的识别结果准确率，图13为各试验工况Softmax-score。

表8 试验的损伤模式识别准确率Tab.8 Damage pattern identification accuracy rate of experiment

从识别准确率不难看出，各模型损伤四根杆件杆工况准确率普遍高于损伤两个杆件准确率，且其Softmax- score也更为突出，一定程度上表明模型对强损伤工况更为敏感，但整体而言BO-BiLSTM模型识别精度依旧保持良好。具体从各模型结果分析，虽然BO-LSTM与BiLSTM模型对损伤4根杆件识别效果略优于BO-BiLSTM模型，但实际准确率上差别不大；而对于损伤两根杆件的工况而言，BiLSTM模型和BO-LSTM模型对部分工况识别效果很差，甚至完全失去判断能力，而BO-BiLSTM模型仍保有较为不错的识别精度,识别更加稳定。

对比试验与有限元模型准确率，由于训练BO-BiLSTM模型的有限元数据并未包含噪声，因此有限元模拟数据集的识别精度都高于试验数据集，但两者精度并未存在过大差距。在实际试验过程中，试验场地具有较大且复杂的环境噪声(如人员走动、液压机的振动、开关门、空调等等)，BO-BiLSTM模型对试验测试集识别精度仍保持在一个较高水平，由此可知BO-BiLSTM模型在结构的损伤识别的实际应用过程中具有较好的抗噪能力和鲁棒性。

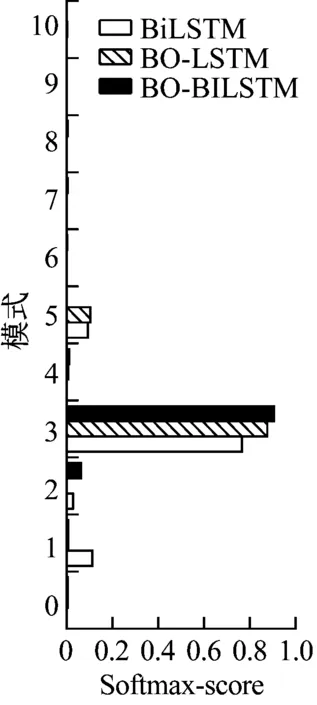
图13 试验的损伤模式识别结果Fig.13 Damage pattern identification results of experiment

5 结 论

本文提出了一种基于贝叶斯优化的BiLSTM模型的损伤识别方法，该方法运用贝叶斯优化选取BiLSTM模型的超参数组合，通过结构加速度响应数据训练模型，使其具备损伤识别能力。采用输电塔有限元模型损伤试验验证了提出方法的有效性，并对一个实际输电塔结构进行了试验研究，结果表明：

(1) 本文提出的损伤识别方法能够有效识别输电塔结构的层间损伤。以结构不同损伤状态下加速度响应作为输入数据，经过训练后的BO-BiLSTM模型可以判断其损伤的位置与损伤模式。

(2) BiLSTM模型的超参数与模型性能密切相关。从输电塔有限元试验中得知，贝叶斯优化可以有效的运用于BiLSTM模型的超参数选取，充分利用历史信息选取最优超参数组合，提高搜索效率。

(3) BO-BiLSTM模型可以采用异源数据(有限元模拟和振动台试验)进行损伤识别。有限元模拟的方法可以获得大量不同损伤工况下的加速度样本作为训练集，训练用于输电塔损伤识别的BO-BiLSTM模型，提取结构损伤特征信息，再将之应用于实际结构的损伤诊断之中。

本研究通过有限元模型模拟部分损伤工况，以此作为训练集训练长短时记忆网络，并以试验数据验证该方法的有效性。由于实际可能出现的工况种类众多，模型模拟的数据量庞大，对网络模型的要求更高，受试验条件限制本文模型试验中无法涵盖所有可能出现的损伤工况，故应用于实际中仍有待进一步研究。