超长期循环荷载作用下海上风机大直径单桩动力特性演变规律研究
龚 敏,朱 涛,陈守祥,张东明,贺 瑞
(1.中南电力设计院,武汉 430071;2.河海大学 港口海岸与近海工程学院,南京 210098)
大直径单桩基础是指直径3~8 m,壁厚30~60 mm,长径比2~10的大直径钢管桩,其优点在于造价较低、施工方便、施工周期短、受环境制约小,并且可以适用于黏土、粉土、砂土等各种海床中[1]。因此大直径单桩在全世界范围内得到了广泛应用。近海风机是典型的建立在海底基础上的高耸柔性结构,自振频率较低,和海上风机运行期间受到的风、浪、流、地震波以及运行荷载等动荷载的频率接近。因此需要对大直径单桩的振动特性进行精确的控制从而避免发生共振。
目前对于海上风机大直径单桩基础的初始振动特性的理论计算和数值模拟相对成熟,包括:Winkler动力弹簧模型[2-3],Novak薄层法[4],Muki和Sternberg的虚拟桩法[5]和Pak积分方程方法[6-7]等。数值模拟方面[8-10],众多学者通过有限单元法研究了基础动力特性(动刚度、共振频率、阻尼比等)随长径比(L/D)、厚径比(h/D)、弹模比(Ep/Es)、无量纲频率(a0)等参数的变化。长期循环荷载的研究目前主要集中于累积变形及刚度变化的研究[11-17],但是长期循环荷载也会从多个方面影响大直径单桩的振动特性:根据土动力学知识,土体的动剪切模量、阻尼比等参数会随动荷载产生的剪切应变幅值变化;也会随循环加载次数增加而变化;土体在往复荷载作用下,土颗粒之间发生相对滑移会产生新的排列,不仅仅会导致桩周土体的振密,根据Cuéllar等[18]的研究,在达到一定循环荷载幅值时,桩周土体颗粒落在桩土间隙当中从而产生对流运动,最终形成振动坑,这种土颗粒的运动也可能加剧现实海洋环境中桩周土体在波流作用下的冲刷。Lombardi等[19]研究了海上风机基础在黏性土中,经历32 000~172 000次水平循环荷载作用过程中桩基共振频率和阻尼比的变化,试验结果显示在黏性土中,循环荷载长期作用会导致桩基水平动刚度的降低从而导致桩基水平共振频率降低,降低程度和桩周土体剪切应变幅值线性相关,和循环次数对数相关;阻尼比随着循环加载次数呈增大趋势。LeBlanc等[20]进行了一系列的室内模型试验,发现单桩基础在8 000~60 000次循环荷载作用后的转角累积变形和刚度变化。Arshad等[21]通过室内1g模型试验,发现6 000次循环荷载作用过程中大直径单桩刚度因砂土振密而增加。Li等[22]通过二维的板代替桩基详细地研究了长期循环荷载作用过程中桩周土体颗粒的对流运动情况,同时研究了共振频率的变化。但是上述研究中,Lombardi研究对象为黏性土,没有研究过砂土;LeBlanc主要研究对象是转角累积变形和刚度变化;Arshad循环加载次数较少,并且试验中没有观察并考虑砂土振动坑的影响;Li的研究中,将桩基简化而二维板,主要研究对象为桩周土体的颗粒运动,不能很好地考虑与实际桩基的力学相似关系。目前海上风机大直径单桩基础理论方法、数值方法大多只能对其初始振动特性进行计算,而无法考虑海洋环境下循环荷载(如波浪荷载)长期作用过程中大直径单桩基础的振动特性变化。因此本文采用室内1g模型试验的方法,着重研究了大直径单桩模型在长期循环荷载过程中水平振动共振频率、阻尼比和刚度的变化规律。
1 试验方案
1.1 试验内容与方法
1.1.1 水平静力承载力试验
在中密砂(相对密实度Dr=63%)中进行大直径单桩水平静力承载力试验,确定桩基水平静力承载力Hu,作为循环荷载幅值大小的参考。桩基水平承载力取桩顶位移达到0.1D时对应的水平荷载。加载方式根据JTG 254—1998《港口工程桩基规范》[23]进行加载:加载过程约分为10个阶段,每次加载约0.1Hu,(Hu通过预试验和数值模拟进行估算)。当加载点的位移变化率在30 min内小于1×10-5m/min时,开始下一阶段的加载,当总位移达到0.1D时停止加载。
1.2 不同幅值的循环荷载长期加载试验
(1) 循环荷载加载幅值
通过室内1g模型试验,对钢管桩模型进行不同幅值循环荷载长期作用后的桩基动力特性测试试验,循环荷载幅值取0~0.3Hu。由水平静承载力试验可知,试验桩在该密实度砂土中水平承载力为60 N,如图1所示。海上风机大直径单桩基础所受的长期循环荷载例如波浪荷载的幅值大约在30%Hu。因此,本文试验中循环荷载幅值取5%,10%,20%,30%Hu,分别为3N,6 N,12 N,18 N(3 N由于传感器原因没有分析时域结果,3 N荷载较小,长期循环加载对桩土结构的影响很小)。

图1 桩基水平承载力试验Fig.1 Static pile-head response
(2) 循环荷载加载频率
试验中通过动力相似关系将现实中的海浪频率换算至试验中,保证试验与原型无量纲频率a0[24]一致,如式(1)。
(1)

(2)

(3)
式中:fp为现实中海浪频率,约为0.2~1 Hz,则试验中对应的加载频率fm约为6.32~31.6 Hz,但是试验中若使用该频率区间的正弦荷载进行加载,要想达到107量级的加载次数,加载时间过长,因此,考虑将该频率f1(fm)对应的在桩顶初始水平振动频响函数曲线上纵坐标数值相同的频率f2作为试验中的加载频率,如图2所示。取实际fp=1 Hz,fm=30 Hz。据此确定试验中所施加正弦荷载频率为112 Hz。由图2可知,在加载频率为f1或f2时,桩顶达到的响应幅值接近,对桩土结构振动特性变化的影响也是相近的。

图2 试验加载频率确定Fig.2 Determination of the loading frequency
(3) 振动特性测试方法
本文通过白噪声分析得到桩顶水平位移的频响函数:对桩顶施加随机荷载,并同步采集桩顶所受荷载x(t)和桩顶水平位移y(t),将所测时域数据通过快速傅里叶变换从时域变换到频域X(ω),Y(ω),系统相应的频响函数H(ω)为Y(ω),X(ω)之比。根据频响函数曲线可以进而得到桩基共振频率、阻尼等结构参数[27]。
1.2 试验布置
1.2.1 试验箱及加载装置
试验在河海大学港航结构实验室的近海岩土工程实验室内进行。由于不同组次试验之后桩土受到扰动,应力应变状态发生变化,需要进行多次砂土的置换,因此试验将在长×宽×高为0.6×0.6×1.0 m的铁箱中进行。铁箱中装满干砂。为了方便试验结束后排砂换砂,试验箱被架高40 cm,底部开一圆孔并安装阀门。
桩顶侧向循环荷载通过激振器施加。激振器可以对桩顶施加简谐荷载、扫频荷载和随机荷载等。静荷载通过在激振器另一侧的定滑轮上放置重物施加。如图3所示。

图3 试验布置示意图Fig.3 Testing layout
1.2.2 试验土性质及制备
试验所用石英砂粒径为0.2~0.6 mm,中值粒径0.42 mm,最小干密度1.28 g/cm3,最大干密度1.57 g/cm3。级配曲线如图4所示。砂土的摩擦角约为30°。

图4 试验砂土级配曲线Fig.4 Sand gradation curve
本文中相对密实度63%的砂土制备采用从最低的高度分层人工填筑的方式,每层10 cm,共十层。根据每层所填砂土的质量和体积计算出松砂的密度约为ρ=1.45 g/cm3。在已知每层砂子体积的条件下,可以计算出每层所填质量应为52.26 kg,每一层填完之后进行夯实,直到砂面到达每层对应的深度。
1.2.3 模型桩制作及安装
贺瑞指出大直径单桩基础的动阻抗与桩基埋入土体部分的长径比L/D和厚径比h/D等参数有关。相比于传统陆上风电的桩基基础,海上风机大直径单桩有着更小的长径比,约3~8;厚径比约0.01。试验中模型桩L/D取5,h/D取0.01。试验中模型桩为钢材,弹性模量Ep=210 GPa,直径D=60 mm,总长L0=600 mm,入土深度L和露出土面长度H均为300 mm,壁厚0.6 mm,缩小比例约为1∶100,模型桩放置于试验箱中心位置,通过锤击打入砂土中指定深度。根据试验中的桩土条件,计算Poulos[28]的桩土相对刚度系数Kr=(EpIp)/(EsL4)=0.64(其中EpIp为桩基截面抗弯刚度,Es为土体弹性模量,L为桩基埋深;Kr<0.002 5为柔性桩,Kr>0.208为刚性桩),因此试验中桩基为刚性桩。
1.2.4 试验仪器布置及数据采集
激振试验中,激振器须与信号发生器、功率放大器及计算机组成激励系统。数据采集装置主要包括位移传感器、力传感器、加速度传感器等传感器,其与信号采集器相连,并通过计算机进行采集。
2 试验结果及分析
2.1 长期循环加载时域数据
通过激振器施加固定频率(112 Hz)、不同幅值(3 N/6 N/12 N/18 N)的稳态正弦循环荷载于桩基顶,同组试验中加载幅值保持恒定。通过电涡流位移传感器和力传感器等拾振设备采集桩顶位移(ut)及所受荷载(Ft)的时域数据。加载到一定循环次数之后停止加载,通过激振器施加小幅值的随机荷载并进行频响分析从而得到桩基振动特性变化。由于数据采集时采样频率高,采样时间长,数据量过大,无法导出,因此分段将位移时程曲线图片按照相同比例拼接,如图5所示。桩顶荷载-位移时程关系曲线同样也被分段展示,并将测试软件中导出的图片拼在一起,如图6所示,可以看出在加载前期,滞回曲线有明显的累积偏移,而随着加载次数增加,滞回曲线逐渐稳定。图6未标出坐标轴,因为展示时域滞回曲线的主要目的在于通过滞回曲线看出位移的累积,可以明显看出刚度(椭圆顶点连线斜率)的变化。
由图5的桩顶位移时程曲线可以看出,尽管在桩顶施加的是对称的水平正弦循环荷载,但是在加载早期,会有非常明显的累积位移现象,并且位移累积的方向也是一致的。这是由于土体填筑过程中总有或多或少的不均匀,在循环加载过程当中,土体颗粒会重新分布排列,因而产生永远无法恢复的塑性变形,随后持续累积,在一定循环次数之后达到稳定。位移累积方向一致是因为桩顶所加荷载初始方向总是一致的,在一个正弦循环荷载周期内,前半周期内正向加载产生的位移总要比后半周期的反向位移大,因此只要初始的荷载方向一致,位移累积的方向也是一致的。从图中还可以看出,不同幅值(6~18 N)循环荷载作用下,累积位移稳定时的桩顶位移累积值均在0.7 mm左右,这是因为对称循环荷载作用下,累积位移受荷载幅值大小影响较小,主要受砂土初始密实度影响,但是达到累积位移最大值所需加载次数随荷载幅值增大而减小,6 N,12 N,18 N累积位移达到最大值时加载次数分别约为40万次,20万次和10万次。图5(c)中,幅值为18 N的循环荷载作用下桩顶位移先累积增大再略微减小然后达到稳定,这是因为荷载幅值较大时,桩周土体振密效果更为明显,土体密实度增大后体现出密砂的剪胀性质,土体体积增大,发生回弹,导致桩顶累积位移略微减小,最后再达到稳定。

(a) 荷载幅值6 N-10%Hu
2.2 长期循环加载过程振动特性变化
2.2.1 循环加载过程中桩基随机激励频响函数
在施加正弦循环荷载一定次数后,停止施加正弦荷载,改为施加较小荷载幅值(约为1 N)的扫频激励,扫频激励荷载幅值应尽量小,从而尽可能减少该测量过程对桩周土体的扰动,扫频激励频率范围20~200 Hz。
不同幅值循环荷载分别作用不同次数之后桩基水平振动频响函数如图7(a)、(b)、(c)所示。图中云图颜色表示频响函数FRF与最大值的比值,以突出频响函数峰值从而更易观察共振频率的变化。

(a) 荷载幅值6 N(10%Hu)
2.2.2 长期循环荷载作用过程中桩顶水平共振频率变化
根据2.2.1中所测量并计算出的频响函数,取频响函数最大值所对应的频率为桩基水平共振频率,可以得到桩基在不同幅值的循环荷载长期作用过程中共振频率的变化。受到人工填土的影响,每一次填土完成所得到的桩土结构初始共振频率fn-initial不可能完全一致,所以本文中主要考虑N次循环加载之后桩基共振频率fn-N与桩基初始共振频率fn-initial的比值,即fn-N/fn-initial随循环加载次数N的变化。
图8展示了桩顶水平共振频率随循环次数N的变化,可以从中得出以下规律:① 在小幅值(5%Hu)加载过程中,共振频率变化不大,fn-N/fn-initial约在0.97~1.0。② 桩顶循环荷载幅值为10%Hu,桩顶水平共振频率先增大后保持不变,约100万次循环加载之后,fn-N/fn-initial稳定在1.05左右。桩基共振频率略微增加的原因主要是循环荷载对桩周砂土的致密作用,荷载较小时,这种致密效果并不明显,并在加载约百万次之后达到稳定。③ 随着荷载幅值增大,共振频率增大幅度也随之增大。这是因为荷载幅度的增大导致循环荷载的致密效果更为明显。④ 桩顶循环荷载幅值为20%Hu和30%Hu时,桩顶共振频率变化趋势非常相似,整体而言随循环次数增大而增大,但是过程中时常有减小再增大的情况出现。这种现象主要由两方面的因素造成,一是循环荷载对砂土的致密作用,导致桩周土体刚度增大,共振频率增加;二是循环荷载较大时,桩基与桩周土体之间的间隙超过土体颗粒粒径,导致土体颗粒落入间隙中,桩周形成振动坑,导致桩基入土深度有所减少,使桩基共振频率有所降低。

(a) 循环荷载幅值6 N
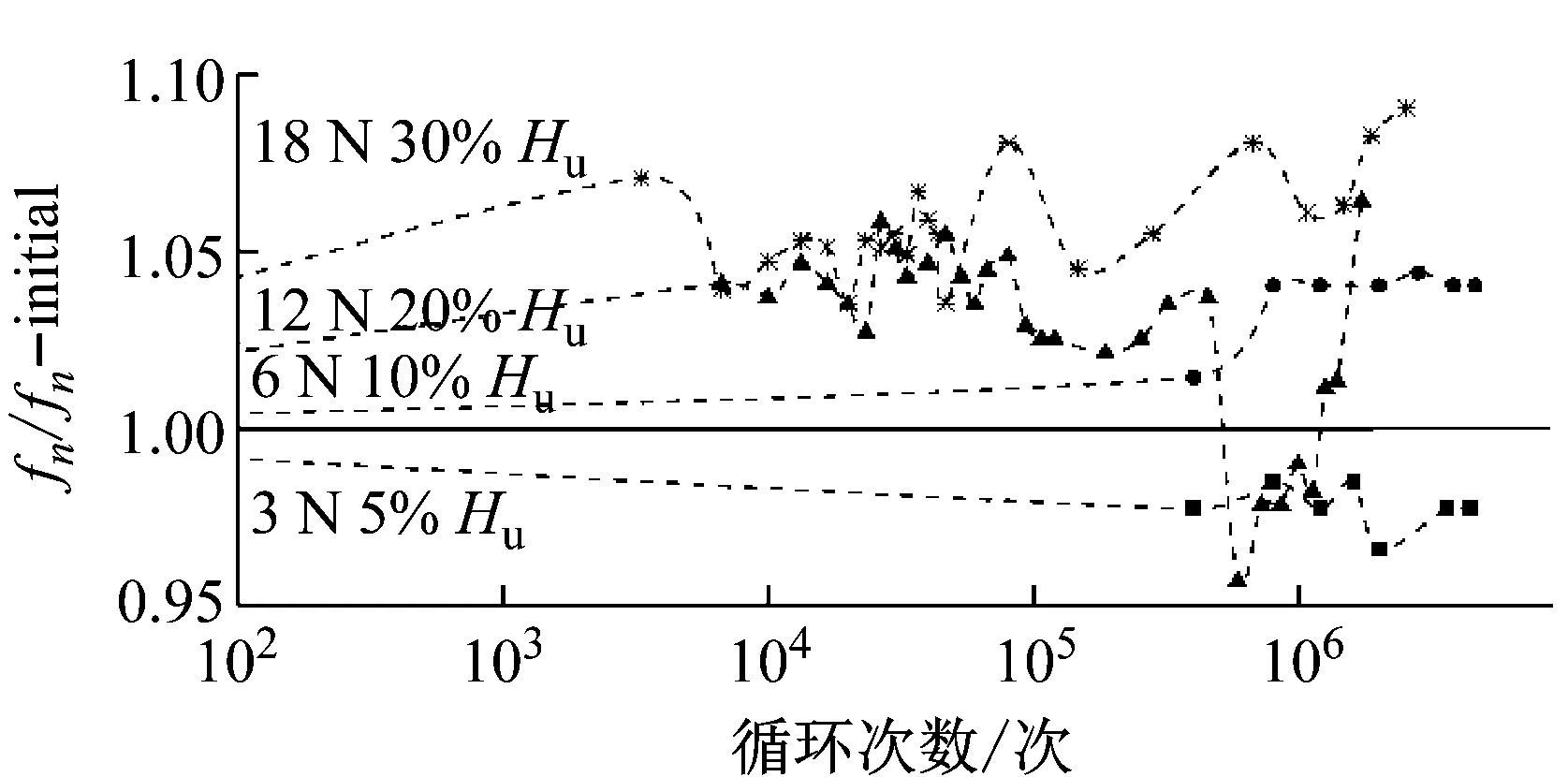
图8 桩顶水平共振频率随循环次数变化Fig.8 Variation of pile-head horizontal resonance frequency with the number of cyclic loadings
2.2.3 长期循环荷载作用过程中阻尼比变化
阻尼比ξ是反应土体动力特性的一个重要参数,桩土动力相互作用过程中,阻尼的存在可以起到削减桩基振动幅值的作用,减小桩基共振危害。桩土动力相互作用中的阻尼比包括土体辐射阻尼,土体材料阻尼,桩土接触面能量消耗产生的阻尼等等。桩土系统的阻尼比ξ[29]可以通过土体滞回曲线进行计算,如图9及式4所示,通过求出任一循环周期的滞回圈面积和三角形OAA′的面积即可计算出阻尼比,并得到阻尼比随着循环次数的变化规律。
(4)
根据图10不同幅值循环荷载作用下阻尼比随循环次数变化曲线,可以看出:在百万至千万次循环荷载作用过程中,桩土系统阻尼比随加载次数增加呈下降趋势;循环荷载幅值越大,阻尼比降低幅度越大。
阻尼比随循环加载次数呈下降趋势,这是因为在循环加载过程当中,桩周土体密实度增加,导致阻尼比降低[30]。振动波在疏松介质中的传播更容易被削弱(例如在用于隔振的泡沫板、橡胶垫中),而在密实介质中振动的能量更容易传播,因此,随着桩周土体密实度的增加,桩土结构阻尼比也随之减小,Hardin等得到的经验公式也能证实这一点,如式5,洁净干砂中最大阻尼比随循环次数N增大而对数减小。
洁净干砂:ξmax=33-1.5lg(N)
(5)
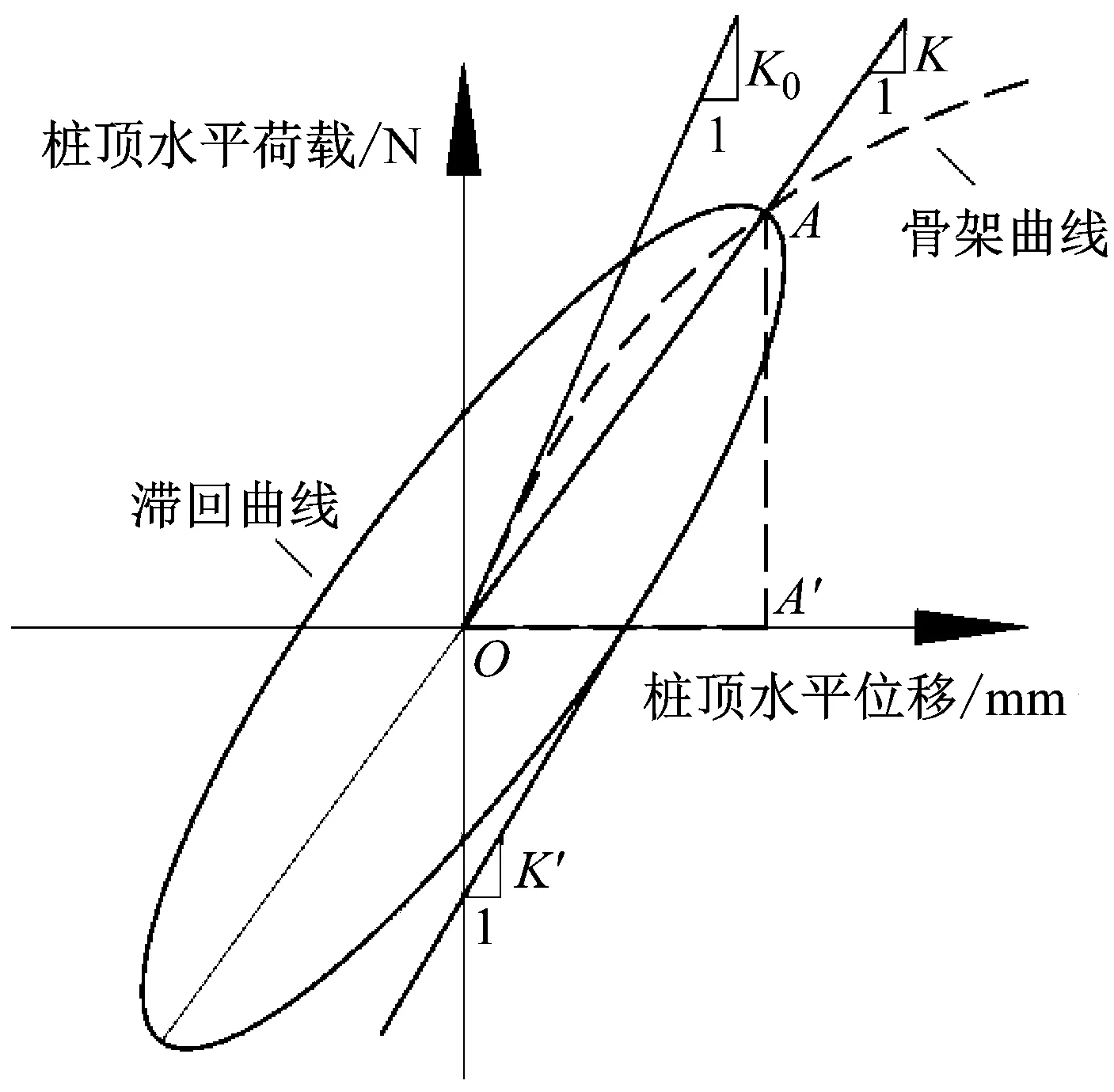
图9 桩顶荷载-位移滞回曲线Fig.9 Pile-head load-displacement curve

图10 不同次数循环加载过程中阻尼比变化Fig.10 Variation of damping ratio with the number of cyclic loadings
2.3 长期循环荷载作用过程中桩顶水平刚度变化
土在动荷载作用下的变形常包括弹性变形和塑性变形,当动荷载幅值较小时,主要为弹性变形,随着动荷载的增大,土体开始出现不可恢复的塑性变形,引起土体剪切模量随着应变衰减。在长期循环荷载加载过程中,土体剪切模量如何变化是衡量土体动力力学性质的重要标准,但是土体的应力应变状态一般只能通过单元体试验进行测量,在桩基振动试验中是很难进行准确量测的,因此,本文中主要考虑整体桩土结构的桩顶刚度K的变化。图9为某一循环周期内桩顶位移-桩顶水平荷载滞回曲线及桩顶荷载-位移骨架曲线,其中K0为土体小应变即桩顶位移很小的时候桩顶初始刚度,K为某幅值的循环荷载作用下桩顶割线刚度,K′为某一循环的卸载过程中的桩顶卸载刚度。研究桩顶割线刚度在不同幅值的循环荷载长期作用过程中的变化有助于了解海上风机大直径单桩在长期的循环荷载作用过程中刚度的演变规律。
图11(a)、(b)所示,对于加载刚度(割线刚度):①循环荷载幅值为3 N,6 N时,桩顶水平割线刚度随循环加载次数变化不大,KN/Kinitial稳定在1左右,而6 N加载过程中桩顶割线刚度小于3 N割线刚度,此时,两组试验刚度关系满足土体剪切模量随着应变增大而衰减的规律;②但是当荷载增大到18 N时,桩顶割线刚度相对6 N时又有增大,这里是因为18 N荷载作用下,桩周土体会以较快的速度被振密,导致土体刚度增加,但是在较大荷载作用下,土体应变也很大,因此割线刚度没有超过3 N的试验组次;③在循环荷载幅值为18 N的加载过程中,桩顶割线刚度呈下降趋势,KN/Kinitial<1,最终趋于稳定,约为初始割线刚度的85%,这是因为随着加载次数增加,桩周土体逐渐形成了振动坑,在土体密实度已经稳定之后,振动坑的形成导致桩基入土深度减小,使得桩基割线刚度减小,随着振动坑也稳定下来,桩基割线刚度也随之稳定。

(a) 桩顶水平刚度
如图11(a) 、(b)所示,对于卸载刚度:①卸载刚度总体要大于割线刚度,因为在卸载至荷载接近0时,桩周土体会处于较小的应变状态,因此卸载刚度要更大;②卸载刚度随循环加载次数整体呈增大趋势,KN/Kinitial>1,3 N加载过程KN/Kinitial略大于1,6 N加载过程中卸载刚度增大趋势明显,最终达到稳定,卸载刚度约为初始卸载刚度的1.25倍。这主要是受到振密作用的影响,桩周土体逐渐变密,卸载刚度增加,而18 N加载过程中整体上卸载刚度相比于初始卸载刚度有所增大,但是随着加载次数增加又开始有下降的趋势,这是由于在此过程当中,卸载刚度受到振密作用带来的刚度增大和振动坑的形成造成的刚度减小这两方面的影响。从试验结果可以看出,土体振密导致的桩基卸载刚度先增大,而振动坑的形成和发展需要一定的时间,因此在一定加载次数之后桩基卸载刚度才会开始减小。
3 结 论
本文采用频响分析法分析了模型桩在不同幅值的循环荷载长期作用过程中振动特性的变化,根据不同幅值的循环荷载加载过程中的桩顶水平荷载-位移滞回曲线分析了阻尼比、桩顶水平割线刚度、卸载刚度随循环加载次数的变化规律。根据试验数据可以看出:
(1) 桩基共振频率随循环次数总体呈增大趋势,荷载幅值较小时(10%Hu),桩顶共振频率主要受桩周土体振密的影响,随着循环次数逐渐增大,fn-N/fn-initial最后稳定在1.05左右;当荷载更大(30%Hu)时,桩周共振频率受土体密实度增加和振动坑的形成这两方面的影响,桩周形成振动坑,导致桩基共振频率在受振密效果增大后再降低,fn-N/fn-initial达到最大值约1.10。
(2) 总体来看,桩土系统阻尼比随循环加载次数呈下降趋势;循环荷载幅值为6 N(10%Hu)的加载过程中,阻尼比相较3 N(5%Hu)加载过程整体趋势接近,但是阻尼比略大,此时阻尼比主要受到土体剪切应变的影响;循环荷载幅值为18 N(30%Hu)的加载过程中,阻尼比相对于3 N,6 N加载过程明显减小,这是因为此时土体密实度增加导致的阻尼比减小效果相比于剪切应变增大导致的阻尼比增大效果更为明显。
(3) 当荷载幅值较小时,桩顶水平割线刚度随循环次数增加变化不大;当循环荷载幅值较大时,桩顶水平割线刚度随着循环次数的增加呈下降趋势,18 N(30%Hu)循环加载过程中,割线刚度稳定时约为初始值的85%,这是由于桩基周围形成的振动坑导致的桩基入土深度的减小;
(4) 桩基水平卸载刚度随加载次数主要呈增大趋势,3 N(5%Hu)加载过程KN/Kinitial略大于1,6 N (10%Hu)加载过程中卸载刚度增大趋势明显,最终达到稳定,卸载刚度约为初始卸载刚度的1.25倍,这主要是受到振密作用的影响,桩周土体逐渐变密,卸载刚度增加。而18 N(30%Hu)加载过程中整体上卸载刚度相比于初始卸载刚度有所增大,但是随着加载次数增加又开始有下降的趋势,这是由于在此过程当中,卸载刚度受到振密作用带来的刚度增大和振动坑的形成造成的刚度减小这两方面的影响。从试验结果可以看出,土体振密导致的桩基卸载刚度先增大,而振动坑的形成和发展需要一定的时间,因此在一定加载次数之后桩基卸载刚度才会开始较小。
为了进行室内1g模型试验研究,本文对海上风机大直径单桩基础的振动特性研究问题进行了一些简化:将桩顶风机叶片和机舱简化为质量块;土的应力水平低于现场情况,并认为单桩只表现为刚性;将饱和砂土的排水条件模拟为干砂土。为了进一步研究长期循环荷载作用过程中海上风机大直径单桩振动特性,需要考虑不同海底地质条件、土壤应力水平、排水条件以及实际波浪、水流和风荷载;需要建立能够考虑土体非线性的有限元动力分析数值模型。

