冲击荷载下含层理介质动态裂纹扩展特性研究

王雁冰，付代睿，吴后为，耿延杰，张瑶瑶

1) 中国矿业大学（北京）力学与建筑工程学院，北京 100083 2) 深部岩土力学与地下工程国家重点实验室，北京 100083

天然岩体中夹杂着大量的节理，裂隙，孔洞等缺陷，在井巷，边坡等定向断裂控制爆破工程中，这些缺陷势必会对爆生裂纹的扩展产生影响，改变其力学和运动学行为，甚至会影响整个工程爆破的质量.因此，研究含缺陷介质在冲击荷载下的断裂特征和裂纹扩展行为具有重要的理论价值和应用前景.

许多学者利用不同的方法从不同的角度对此问题进行了相关研究，取得了一些初步的成果.李地元等[1]采用万能材料试验机和分离式霍普金森压杆(SHPB)置，对不同裂隙角度的花岗岩圆柱试件进行了3种不同方式加载试验，借助三维数字图像相关法（3D-DIC），发现各加载方式下裂隙角度改变对其强度、峰值应变及弹性模量的影响.王奇智等[2]采用SHPB装置和数字图像相关（DIC）技术，对含不同角度双节理试件进行动态冲击试验，发现试件强度、破坏模式和应力强度因子均受节理角度影响.刘晓辉等[3]利用SHPB装置对垂直和平行2种层理方向煤岩试件进行了巴西劈裂试验，分析了抗拉强度与层理方向的关系.李超等[4]采用改进的动态版RFPA2D数值模拟软件，对动载下节理岩体的动态破坏过程进行了模拟，重点讨论了节理参数及应力波峰值对岩体动态破坏过程的影响规律.Wu等[5]通过现场试验，分析了节理数量等参数对爆炸应力波传播的影响.廖志毅等[6]通过数值模拟分析了节理岩体在刀具动态荷载作用下的损伤破裂过程，探讨了节理间距和节理角度的影响.Cai等[7]研究了岩体中多组平行缺陷对应力波传播的影响.李夕兵等[8]建立了不同频率载荷作用下的岩石节理本构模型.Li与Ma[9]研究了应力波在填充节理中的传播规律.王雁冰等[10]研究了含层理煤的动态断裂特征.李淼[11]从能量角度出发，分析冲击荷载作用下单节理岩石的能量耗散规律及其各向异性特征.李娜娜等[12]采用分离式霍普金森压杆试验装置开展试验研究，分析不同接触面积比的节理的动态力学特性以及节理的接触面积几何分布对应力波传播特性的影响.杨立云等[13]研究了偏置裂纹对含双裂纹PMMA试件动态断裂影响效应.Siegmund等[14]采用数值模拟方法研究了动态裂纹穿越界面时裂纹尖端应力场的变化特征，发现裂纹在遇到弱面后，可能出现沿弱面扩展和穿越弱面扩展两种形式.Sundaram与Tippur[15]分析了双介质材料中裂纹扩展的动态断裂特性.李地元等[16-17]分别分析了动静作用下含端部裂隙的大理岩的力学性能、裂纹拓展过程的差异.杨阳与杨仁树[18]对低温冻结红砂岩进行动态冲击实验并结合端口形貌分析，探究高应变率下红砂岩动态力学行为.然而，动态荷载具有瞬态性和高加载率的特性，给动态断裂的研究带来的更大的困难，裂纹穿越层理时的动力变化特征研究较少，另外也很少涉及层理的特征参数对裂纹扩展的影响.

现有的研究对于含层理岩石材料的研究较少，且对于其动态破坏机制停留在现象分析阶段，没有借助有效的监测手段解释层理这一缺陷介质对岩石材料的动态力学性能的影响.本文首先利用数字激光动态焦散线实验系统（DLDC）结合离散格子弹簧模型（DLSM），研究了不同预制倾斜角度（30°，45°，60°）的含层理试件的动态断裂特征，分析了裂纹扩展过程中尖端的动力学及运动学参数变化规律，同时分析了层理的弹性模量，厚度对裂纹扩展的影响.DLDC与DLSM数值计算相互验证，相互补充，共同揭示冲击荷载下含缺陷介质的动态裂纹扩展特性.

1 研究方法

1.1 实验概述

实验采用数字激光动态焦散线实验系统（DLDC），如图1，具体介绍参见文献[19-20].试件的材料选择的是透明有机玻璃板（Polymethyl methacrylate, PMMA），有机玻璃板材料性质和力学参数与岩石相近，且透明有机玻璃板是具有良好的光学性质.试件的尺寸示意图如图2，为220 mm×50 mm×6 mm的长条形有机玻璃板，每个试件底边中央设置有一条长度8 mm竖直向上的预制切缝，切缝宽度1 mm且尖端足够尖细以保证试件受到冲击荷载后首先由切缝尖端开裂；定义其宽度方向为y轴方向，长度方向为x轴方向，预制切缝上端20 mm处（设参考点M）预制一层理面，参考点M在坐标轴的位置为（x：0 mm；y：28 mm）.预制层理面制作时，先将试件沿层理方向切开，然后用环氧树脂胶粘合.以层理面与底边夹角θ为控制变量，θ分别为 30°，45°，60°，试件编号分别为试件A，B，C.

图1 数字激光动态焦散线实验系统Fig.1 Digital laser dynamic caustics test system

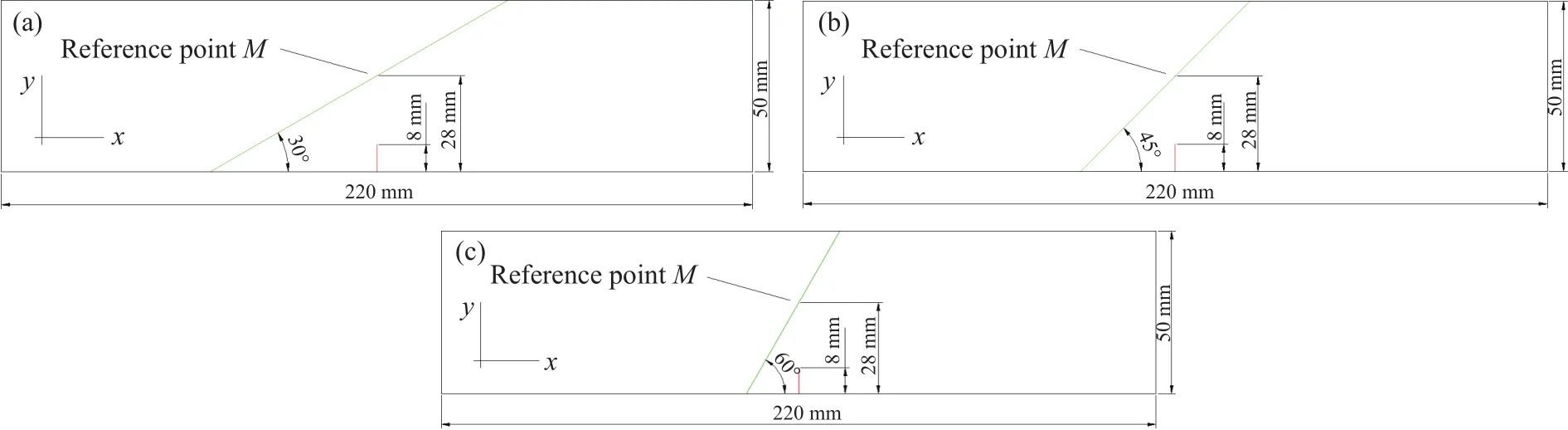
图2 试件示意图.（a）试件 A；（b）试件 B；（c）试件 CFig.2 Diagram of a specimen: (a) specimen A; (b) specimen B; (c) specimen C

本实验的加载系统采用的是落锤加载[21]系统，加载系统的示意图如图3所示，系统主要由落锤、加载头、固定支座组成，落锤重量为1.45 kg，每次实验落锤的下落高度均为330 mm，以保证所有试件在相同加载条件下进行实验.加载头尖端为楔形，实验时对准长条形试件的中线顶端，加载前要检查是否与试件平面垂直，保证试件受到竖向的冲击荷载，并沿预制裂缝开裂.如图3所示两支座内圆柱的间距为214 mm.

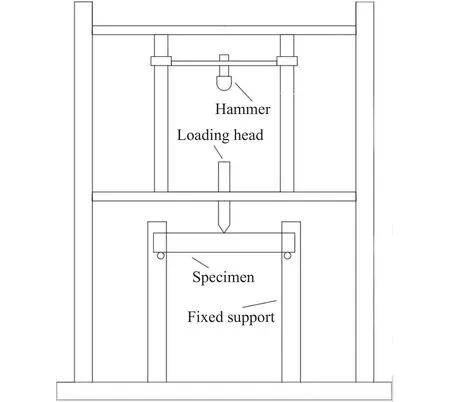
图3 冲击加载装置示意图Fig.3 Diagram of the impact loading device

动态载荷下复合型扩展裂纹尖端的动态应力强度因子[13]：

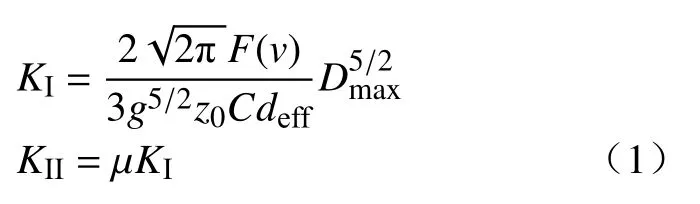
式中，Dmax为沿裂纹方向的焦散斑最大直径；z0为参考平面到物体平面的距离；C为材料的应力光学常数；deff为试件的有效厚度，对于透明材料，板的有效厚度即为板的实际厚度；μ为应力强度因子比例系数；g为应力强度数值因子；KI，KII为动态载荷作用下，复合型扩展裂纹尖端的Ⅰ型和II型动态应力强度因子；F(v)为由裂纹扩展速度引起的修正因子，在具有实际意义的裂纹扩展速度下，其值约等于1.

在该实验中设置高速相机的拍摄速度为100000 fps，图像的分辨率为 320 dpi×192 dpi，最大记录时长为2 s，相邻两幅图片的时间间隔为10 μs.由高速摄影底片获知裂纹在每个时刻对应的扩展长度；由相邻两幅照片裂纹长度的差值，除以两幅照片的时间间隔，即可得到该时间间隔内裂纹扩展的平均速度.

1.2 离散格子弹簧模型

离散格子弹簧模型（DLSM）把介质视作由弹簧连接的一组颗粒[22-23]，是一种基于离散元的方法.该系统的运动方程可表示为：

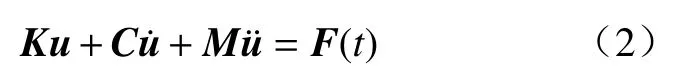
式中，u为颗粒的位移向量；K为系统的弹簧刚度矩阵；M为对角质量矩阵；C为阻尼矩阵；F(t)为外力组成的向量.可通过牛顿定律求解该方程：先给定颗粒位移（初始设置或上个计算步骤的计算结果），即可获得颗粒间的接触形式及弹簧的破坏形态.进而根据给定的位移-荷载关系，可求得各颗粒间的作用力.具体的原理及验证可参考文献[22-25].

1.3 层理介质模型的建立

如图4为以层理角度30°试件为例建立的数值模型.数值模型与实验试件整体尺寸一致，小球颗粒直径设置为0.5 mm，层理设置为一层与有机玻璃板参数不同的小球颗粒，厚度为0.5 mm.模拟中直接采用有机玻璃的物理力学参数，即弹性模量Ed=6.1 GN·m-2，泊松比υd=0.31，密度ρd=1.18 g·cm-3，光学常数c=85 μm2·N-1，弹簧破坏参数Un*=0.005.预制层理为切割后的试件通过环氧树脂粘结形成，根据环氧树脂固化后的物理参数，层理模型参数设置如下：层理的弹性模量E=0.07 GN·m-2，泊松比υ=0.28，密度ρ=1.00 g·cm-3，厚度d=0.5 mm，抗拉强度为23 MPa，抗剪切强度270 MPa，弹簧破坏参数Un*=0.001.层理角度45°和60°试件模型均参照上述过程建立.

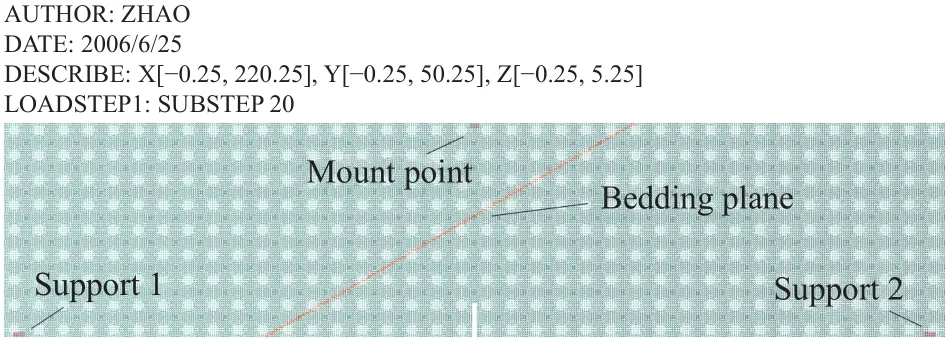
图4 模型建立及加载示意图（层理角度30°）Fig.4 Diagram of model establishment and loading (bedding angle,30°)

模型的边界条件如图4所示，其代表实验中试件的受力状态；由于落锤冲击试件时，支座1、2被固定，于是将左、右支座边界条件设置为数值为0的位移荷载；加载点处的边界条件为实验中试件受到落锤冲击的动态荷载，将加载点处边界条件设置为速度2580 mm·s-1的速度荷载.

2 研究结果及对比分析

2.1 试件破坏后的形态

图5是3组试件的破坏形态及数值计算结果，图6是裂纹扩展过程中拍摄到的系列焦散斑照片.θ=30°时，如图5（a），在层理面上下两侧都出现了明显的裂纹，结合图6（a）可看出裂纹首先由层理面下端的预制切缝尖端开裂，随后竖直向上扩展，在到达第一道层理面后，裂纹没有直接穿透层理沿原方向继续扩展，而是沿层理表面扩展一段距离后，又从层理面中穿出，此后裂纹开始偏向落锤加载点扩展至裂纹止裂.θ=45°时，如图5（b）和图6（b），和试件A相比，裂纹同样沿预制切缝开始起裂，裂纹沿竖直向上方向扩展至层理面，但裂纹没有从层理面中穿出，裂纹沿层理面扩展至试件完全开裂.θ=60°时，如图5（c）和图6（c），整体破坏形态和试件B大致相同.裂纹扩展至层理面后会沿层理弱面扩展，因层理角度的增大，层理面受到的法向剪切应力也随之增大，裂纹倾向沿层理面扩展至完全破坏，而非从层理面上再次起裂.

图5 3 组试件的破坏形态及数值计算结果.（a）试件 A；（b）试件 B；（c）试件 CFig.5 Failure form and numerical results of the three groups of specimens: (a) specimen A; (b) specimen B; (c) specimen C

图6 3 组试件裂纹扩展的动态焦散斑图片.（a）试件 A；（b）试件 B；（c）试件 CFig.6 Dynamic caustics spot image of crack propagation in three groups of specimens: (a) specimen A; (b) specimen B; (c) specimen C

试件的裂纹轨迹以及试件的破坏形态显示，当层理角度小于90°时，裂纹在到达层理后会沿层理弱面扩展一段距离后穿出，而层理角度90°试件的层理与加载方向垂直，层理间各点的受力比较均匀，裂纹扩展并不会受到层理的影响.

对比DLSM数值分析结果可以发现，数值模拟的开裂情况与实验结果有很高的相似度，从裂纹的最终形态来看，3组模型在开裂前期即裂纹从预制切缝起裂到抵达层理面的这段裂纹都为竖直向上扩展，而后，试件A中，裂纹沿层理面扩展一段距离后再次穿出的一条裂纹与实验结果相同，且试件B，C对应模型的裂纹也都没有再次从层理面中穿出，而是沿层理面扩展至试件完全开裂.图5（a）的模拟结果中，从层理面下的裂纹形状来看，裂纹从预制切缝起裂后，沿竖直向上方向扩展，且自始至终非常平直，没有发生明显的弯曲，这和实验结果并非完全一致，实验结果中裂纹在后半段出现了细微的弯曲，这是因为模拟的结果是在相对理想化的条件进行的，试件上部的加载条件为准确对准预制切缝的，而实验可能不完全对准切缝，造成了这种误差；从层理面穿出的裂

纹，和实验结果相比，裂纹在中段以后开始向上偏移，且整体曲线较弯曲，而实验结果整体较平直，这可能是因为模拟的加载条件为恒定的速度荷载，且方向不变，而实际实验中加载速度是会不断变化的，且随着后期试件发生较大的变形，荷载方向也会发生相应的变化.图5（b），5（c）中试件 B，C的模拟结果，从破坏形态来看，两个模型在层理面外侧都只有一条明显裂纹，且裂纹整体都呈现较平直的形态，但值得注意的是，试件B模拟结果的裂纹较弯曲，而实验结果的裂纹为平直的裂纹，这里的原因与之前试件A分析的原因类似.

2.2 裂纹尖端应力特征分析

焦散斑的直径反应了裂纹尖端应力的大小.图6（a）是试件 A的焦散斑图片，0 μs时加载头开始对试件进行冲击作用，随后50 μs后预制切缝尖端开始出现焦散斑，应力波到达预制切缝尖端，随后能量在切缝尖端积聚，焦散斑尺寸不断扩大，并在410 μs时裂纹开始由预制切缝尖端起裂，焦散斑开始沿竖直向上方向扩展，并在490 μs时到达层理面，随后焦散斑转移到层理面中扩展，焦散斑扩展一段距离后，在大约560 μs时沿层理面穿出.图6（b），6（c）分别为试件 B，C 的焦散斑图片，两者在扩展轨迹上相似，且裂纹在穿入层理面后没有再次穿出，在这里放在一起分析，可以看到两试件和试件A一样，焦散斑首先于50 μs时出现，但两者的裂纹起裂时间即焦散斑开始移动的时间分别为 230 μs，190 μs，和试件 A 相比，裂纹起裂的时间明显提前.且随着预制层理倾斜角度的θ增大，裂纹起裂越早.

图7是裂纹扩展过程中动态应力强度因子随时间的变化曲线，只有Ⅰ型动态应力强度因子产生时，裂纹扩展呈现张拉破坏，当出现Ⅱ型动态应力强度因子时，裂纹扩展呈现张拉-剪切复合破坏，而Ⅱ型动态应力强度因子占据主导地位时，裂纹扩展呈现纯剪切破坏.θ=30°时，如图7（a）试件A在裂纹未起裂前的裂纹尖端能量累积阶段只有Ⅰ型应力强度因子产生，它的大小跟焦散斑的直径有关，可以看到曲线并非一直增长，而是在250 μs开始下降，随后在320 μs时又开始增长.由图6（a）的裂纹于420 μs开始扩展，再对照曲线可以知道，此时KⅠ的值为 2.55 MN·m-3/2，即起裂韧度；可以看到此时也开始出现Ⅱ型应力强度因子，裂纹开始出现剪切破坏，且两种应力强度因子接近且一度Ⅱ型动态强度因子大于Ⅰ型，在层理间扩展时，剪切破坏占主导地位.但在之后的裂纹扩展一直小于Ⅰ型应力强度因子，说明裂纹的扩展主要受到Ⅰ型应力强度因子的影响，裂纹以受到拉应力为主.θ=45°时，如图7（b），试件 B 在开裂初期同样只有Ⅰ型应力强度因子，和试件A不同的是，曲线一直向上增长，且在230 μs时到达裂纹扩展的起裂韧度2.86 MN·m-3/2，并且在此时出现Ⅱ型应力强度因子；值得注意的是300～360 μs焦散斑扩展至层理面后短暂地消失了一段时间.θ=60°时，如图7（c），试件 C 的动态断裂韧度为 2.49 MN·m-3/2，Ⅱ型应力强度因子同样是在裂纹开裂时出现，并且在后期与Ⅰ型应力强度因子曲线很相似，拉剪复合应力特征较为明显.

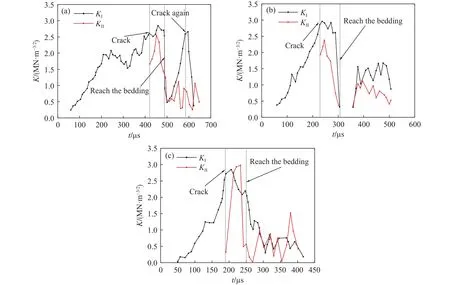
图7 动态应力强度因子随时间的变化曲线.（a）试件 A；（b）试件 B；（c）试件 CFig.7 Variation curve of the dynamic stress intensity factor vs time: (a) specimen A; (b) specimen B; (c) specimen C

2.3 应力波在试件中的传播特性分析

图8是试件A受到冲击荷载后应力波传递的应力云图.0 μs时应力波首先由顶端产生，这是由施加在顶端的速度荷载产生的；应力波在18 μs时到达了层理面，可以看到层理面对应力波有阻碍作用，层理两侧应力云图的颜色有所差异，只有一部分应力波透过层理继续传播.随后在45 μs，应力波传播到了裂纹尖端.这个时刻对应着焦散斑开始出现的时刻，但由于实验条件的限制，相机拍摄时设置的时间间隔是10 μs，所以从起裂时间上看实验结果和数值模拟结果相差5 μs.随后应力波继续传播，直到120 μs，应力云图不再发生大幅度的变化，应力波已经衰减到较弱的程度.图9是θ=45°，θ=60°时，应力波在预制层理处的传播云图.图10是参考点M处y方向应力的变化曲线.不同层理倾角影响应力波的传播，θ=30°时，经层理面反射的应力波整体向倾角较大时，θ=45°，θ=60°时，应力波主要以透射P波为主，反射作用则随着角度的增加逐渐减弱.反方向传播，与后续的应力波在层理面上方形成较强的拉应力区，而透射波P波较少.

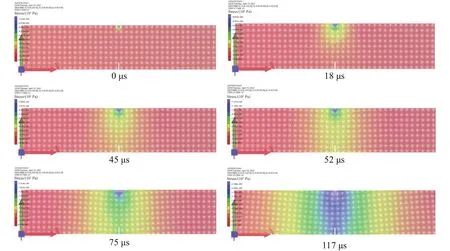
图8 应力波在试件A模型中传递的应力云图Fig.8 Stress cloud map transmitted by stress waves in the specimen A model

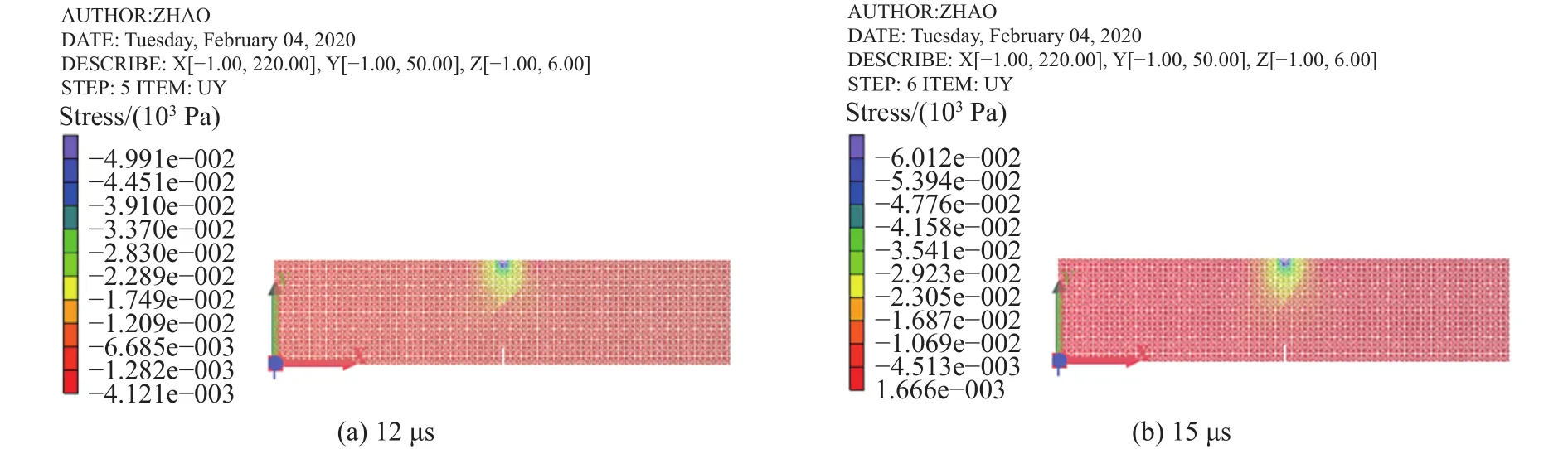
图9 应力波在预制层理处的传播云图.(a)试件B；(b)试件CFig.9 Propagation of stress waves at precast beddings: (a) specimen B; (b) specimen C

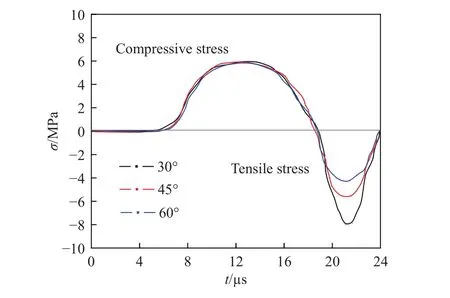
图10 参考点M处y方向应力的变化曲线Fig.10 Variation curve of y-direction stress at reference point M

2.4 裂纹扩展的运动特征分析

图11是裂纹起裂后其扩展速度随时间的变化曲线.从速度变化规律上来看，三种工况下速度的变化规律有一定的差异.如图11（a），θ=30°时，在试件A中，裂纹尖端由起裂到扩展至层理的过程中，速度比较平稳，约为250 m·s-1，只是在快接近层理时速度发生了变化.进入层理后，速度迅速达到峰值，之后快速下降，略微震荡变化后达到第二个峰值.再次起裂后，裂纹扩展速度逐渐减小.如图11（b），θ=45°时，在试件 B 中，在实验结果中，从起裂到扩展至层理的过程中，速度在200 m·s-1左右震荡变化，但DLSM模拟结果中，裂纹扩展起裂后速度迅速增大到一个较大的峰值，310 m·s-1，之后迅速减小，在200 m·s-1左右震荡变化至层理处.在层理中扩展的速度相对较低，且不断震荡变化.如图11（c），θ=60°时，在试件 C 中，起裂到扩展至层理的过程中，速度在225 m·s-1左右震荡变化，在层理内扩展时，则有较大的震荡.裂纹开始沿层理面扩展后，扩展速度均发生不同程度衰减，层理角度越小层理面对于裂纹的径向阻碍作用更大，速度衰减更严重.裂纹遇到层理后停滞扩展并在该处发生应力集中，当裂纹尖端应力强度因子超过层理面的抗剪强度，裂纹开始沿层理面破坏，此时发生剪切破坏，裂纹扩展速度相对在有机玻璃基质中扩展更小.对比实验结果和数值分析结果，可发现两者具有较好的吻合性.两者的大致变化趋势相似，但曲线并未重合.DLSM模拟结果中的起裂时间和实验结果基本一致，但在试件A和C中的起裂速度略有差异，三个试件中裂纹在层理中的扩展速度变化规律也有所差异，这是因为模拟条件是一种理想化的实验条件，加载条件为恒定的速度荷载，且实验材料为非均质材料，而模型为理想的均质材料，另外，因为实验中试件层理为环氧树脂粘结而成，并不能做到完全涂抹均匀，有些部位强度较低，从而裂纹在此处扩展速度较快，造成速度的不均匀.但总体来说DLSM基本能够对冲击荷载下含层理介质动态裂纹扩展进行很好的模拟.

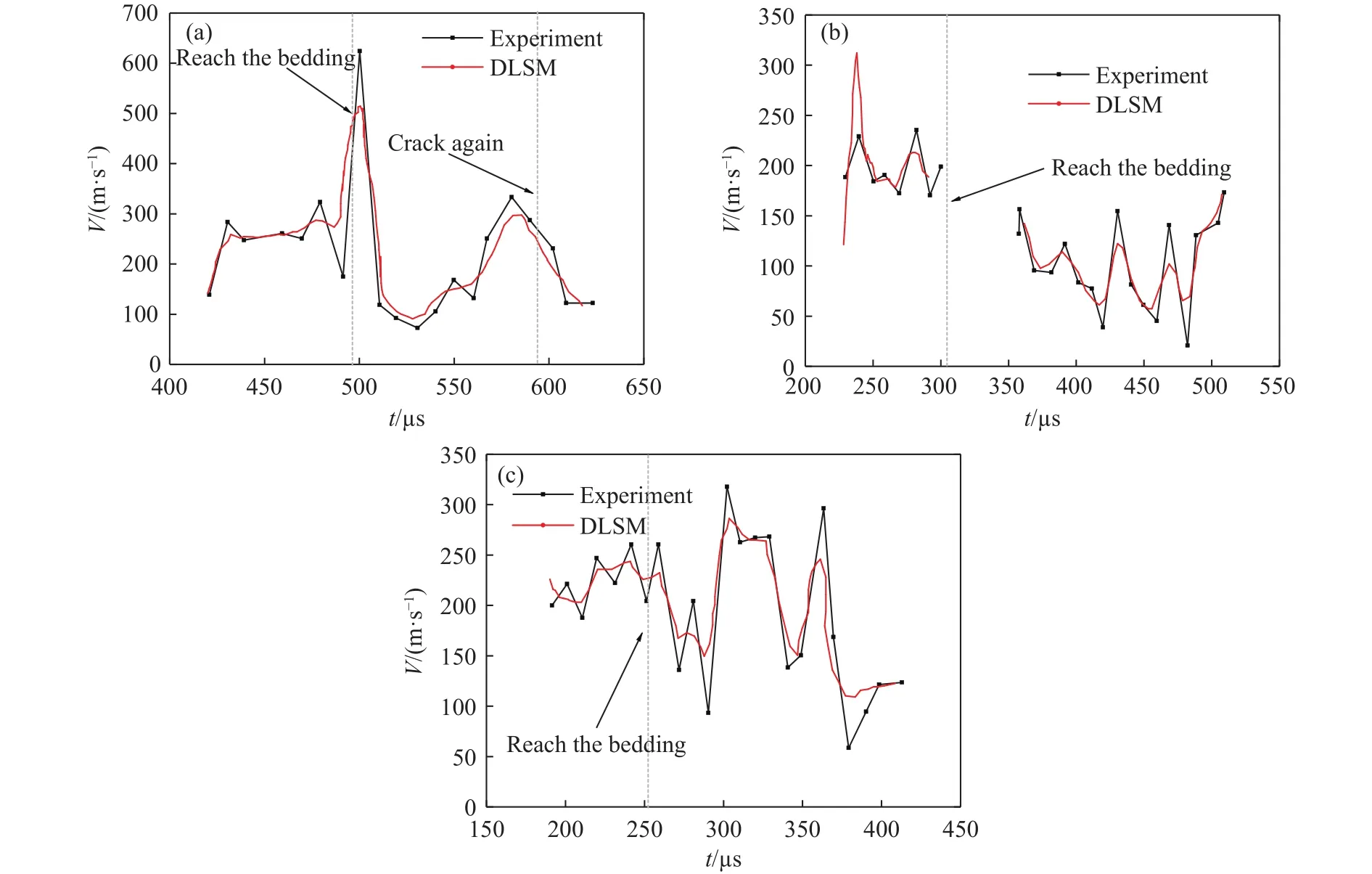
图11 裂纹扩展速度随时间的变化曲线.（a）试件 A；（b）试件 B；（c）试件 CFig.11 Variation curve of crack propagation velocity with time: (a) specimen A; (b) specimen B; (c) specimen C

3 层理参数对数值分析结果的影响

焦散线实验中层理是用环氧树脂胶制作的，其凝固后的物理力学参数不易测定.本节利用DLSM数值分析方法，着重分析层理自身的弹性模量和厚度对介质动态断裂特性的影响.

3.1 层理弹性模量 E对模拟结果的影响

为了研究层理自身的弹性模量对试件开裂情况的影响，设置4组不同弹性模量的模型，模型尺寸参照试件A，即θ为30°的试件，材料参数方面，4组模型层理的弹性模量分别取了0.01，0.04，0.1和0.13 GPa，除弹性模量外其他参数都和试件A相同.

图12是四组不同层理弹性模量模型的开裂结果.图12（a）是E=0.01 GPa的模型开裂结果，前期裂纹扩展和实验及对应模拟结果类似，即裂纹首先从预制切缝尖端开裂，随后近似地沿竖直向上方向扩展，裂纹扩展至层理面，裂纹在穿入层理面后并没有扩展多远的距离就再次从层理面中穿出，且整体方向为竖直向上继续扩展.图12（b）是层E=0.04 GPa的模型开裂结果，前期裂纹和之前并无不同，在这里主要分析后期裂纹，和E=0.01 GPa模型相比，第二条主裂纹沿层理面垂直穿出，移动一小段距离以后在中断位置突然发生变向，转而沿竖直向上方向扩展，另外和前一组相比，裂纹在层理面中扩展的距离也更大.图12（c）是E=0.1 GPa的模型开裂结果，可以看到和前2组相比，裂纹在层理面中扩展的距离更大，该模型裂纹从层理面再次穿出后，是沿层理面垂直穿出，且裂纹始终平直，不发生明显的弯曲，直至模型完全开裂.图12（d）是E=0.13 GPa的模型开裂结果，裂纹在遇到层理时几乎直接穿透层理继续向加载点扩展.综上发现，裂纹在层理面中扩展的距离在0.01～0.1 GPa区间内随层理弹性模量E增大而增大，相同切向应力下产生更大的位移变形量，但大于0.1 GPa时，层理对于有机玻璃基质的粘结作用增大，裂纹倾向直接穿透层理.

图12 不同层理弹性模量条件下模型的开裂结果.（a）E=0.01 GPa；（b）E=0.04 GPa；（c）E=0.1 GPa；（d）E=0.13 GPaFig.12 Cracking results of the model under different elastic moduli of beds: （a）E=0.01 GPa；（b）E=0.04 GPa；（c）E=0.1 GPa；（d）E=0.13 GPa

图13是不同层理弹性模量条件下的裂纹扩展位移，速度对比曲线.图13（a）是4组模型裂纹扩展位移的对比曲线，可以看到裂纹扩展前期，4组模型的曲线极为相似，且几乎重叠，这段时间正好为裂纹沿预制切缝尖端开裂到裂纹扩展至层理面的过程，由于裂纹都近似为竖直向上扩展，所以位移x曲线都在零附近，呈现为直线，而位移y曲线则都直线上升.而从中期以后位移y曲线发生较大的区别，4条曲线组成了一个“梯形”，其中E=0.13 GPa的曲线明显大于其余3组，此后4条曲线又开始重合，后期除E=0.1 GPa的曲线，另外三组曲线重合在一起.而关于位移x曲线，可以看到曲线的峰值对应着裂纹在层理面中扩展的距离长短，可以看到和开裂结果对应的是E=0.1 GPa的曲线峰值最大，即裂纹在层理面中扩展的距离最远.

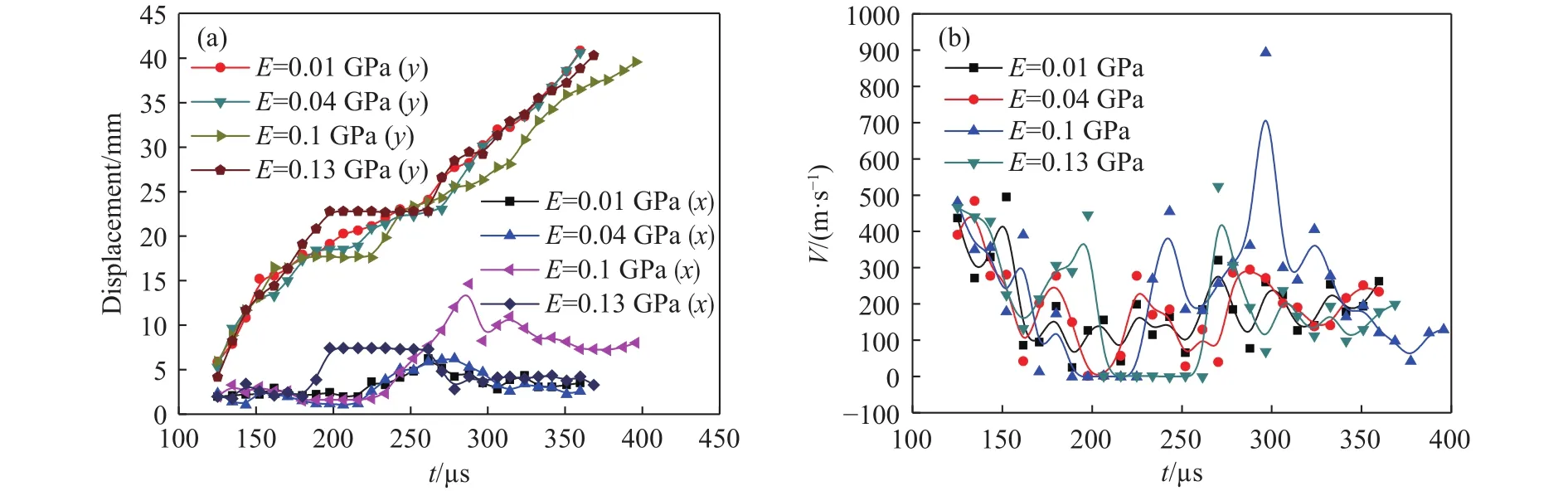
图13 不同层理弹性模量条件下的裂纹扩展位移(a)和速度对比曲线(b)Fig.13 Contrast curves of crack propagation displacement (a) and velocity under different elastic moduli of bedding (b)

图13（b）是4组不同层理弹性模量模型的裂纹扩展速度对比曲线.从起裂速度来看，4组模型的裂纹开裂初始速度分别为439，390，480.5和467 m·s-1，整体来看相差不大，而在裂纹起裂后，4组曲线都发生了振荡下降的现象，说明裂纹开裂时裂纹尖端能量累积较大，随着裂纹开裂，消耗裂纹尖端的能量，裂纹扩展速度开始下降.首先看到E=0.01 GPa的曲线，曲线在从较高的初速开始下降后，在170 μs后开始振荡变化，总体维持在一定的范围内，没有发生较大的变化.E=0.04 GPa的曲线和E=0.01 GPa时的曲线整体类似，只是后期的振荡变化范围比前者更大.而E=0.1 GPa的曲线在后期出现了一大一小两个明显的峰值，即448和890 m·s-1.E=0.13 GPa的曲线出现两个大小非常相近的峰值，488和521 m·s-1.

3.2 层理厚度 d对模拟结果的影响

如图14是不同层理厚度模型的开裂结果.在其他参数不变的情况下，设置了4个不同的层理厚度，d=0.3，0.4，0.6和 0.7 mm.d=0.3 mm的模型，裂纹没有在层理面中扩展，裂纹在到达层理面后沿原方向继续扩展，整体破坏形态接近于无层理模型，裂纹从预制切缝尖端开裂后，裂纹沿竖直向上扩展，裂纹自始至终较为平直，没有发生明显的弯曲.d=0.4 mm的模型裂纹和d=0.3 mm的模型相似，裂纹在扩展至层理面后没有转移到层理面中扩展，而是直接穿透层理面，继续沿竖直向上扩展，但和前者相比，整体裂纹有细微的弯曲，即层理下端裂纹向右弯曲，层理面上端的裂纹向左弯曲.d=0.6 mm的模型和之前的模型类似，即层理面上下端都出现了明显的裂纹，并且相比前两组模型，裂纹首先在层理面中扩展一段距离后再次从层理面中穿出，裂纹沿层理面垂直穿出，且裂纹不是平直的裂纹，裂纹整体向上弯曲，但过渡的较为平滑，不像之前模型一样在裂纹中段突然弯曲.d=0.7 mm的模型裂纹相对之前三组来说，裂纹在层理面中扩展的距离最长，裂纹再次起裂点接近层理面远端，裂纹形态相对d=0.6 mm的模型来说也更加平滑.

图14 不同层理厚度条件下模型的开裂结果.（a）d=0.3 mm；（b）d=0.4 mm；（c）d=0.6 mm；（d）d=0.7 mmFig.14 Cracking results of the model under different bedding thicknesses: (a) d=0.3 mm; (b) d=0.4 mm; (c) d=0.6 mm; (d) d=0.7 mm

图15（a）是不同层理厚度模型的裂纹扩展位移曲线，从位移曲线起始时间来看，d=0.3 mm的模型起裂时间相比其余三组较晚，而其他三组起裂时间很接近.可以看到d=0.3 mm和d=0.4 mm的位移x曲线从始至终没有发生较大改变，再看两者的位移y曲线，d=0.3 mm曲线相比d=0.4 mm的曲线斜率更大，所以虽然前者裂纹起裂时间较后者晚，但两者裂纹止裂时间很相近，虽然两者的裂纹形态很相似，但裂纹扩展速度差别很大.而从位移x的峰值来看，可以看到d=0.7 mm的模型裂纹在层理面扩展的距离最大.

如图15（b）是裂纹扩展的速度对比曲线.d=0.3 mm的模型裂纹起裂速度为514 m·s-1，此后曲线迅速到达一个峰值596 m·s-1，随后曲线开始迅速下降，在裂纹扩展后期，曲线出现两次较小的峰值，398和363 m·s-1，且前后两次峰值出现时间很接近.d=0.4 mm的模型裂纹起裂速度为522 m·s-1，随后便开始持续下降，并在200 μs降低到零并持续一段时间，在240 μs时曲线开始继续上升，随后到达一个峰值494 m·s-1，此后又开始下降，此后曲线出现了第二次明显的峰值357 m·s-1.d=0.6 mm的模型裂纹起裂速度为472 m·s-1，和前一组曲线类似，曲线持续下降，并在一段时间持续为零，此后曲线经历了3次明显的峰值，486，510和382 m·s-1.d=0.7 mm的模型裂纹起裂速度为600 m·s-1，曲线此后持续下降，和其他曲线不同的是，曲线中期没有较大的起伏.

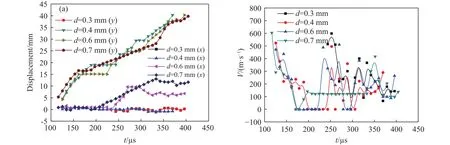
图15 不同层理厚度条件下裂纹扩展的位移（a）和速度对比（b）曲线Fig.15 Displacement (a) and velocity contrast (b) curves of crack propagation under different bedding thicknesses

4 结论

本文利用数字激光动态焦散线实验系统（DLDC）结合离散格子弹簧模型（DLSM）分析了冲击荷载下含层理的PMMA试件的动态断裂特性，本文研究的为人工胶结层理面，与天然岩体中的层理有所差距，在数值模拟基础上尽可能模拟不同条件下的层理参数，以完善相关研究，取得了如下一些结论.

（1）层理角度对实验的破坏形态有着显著的影响.层理角度较低时，裂纹扩展至层理面时会扩展一段距离再次沿层理面上穿出，而层理角度增大后，裂纹更倾向于沿层理弱面一直扩展至完全断裂.

（2）随着预制层理倾斜角度的θ增大，裂纹起裂越早，裂纹在扩展至层理面后沿层理弱面扩展的速度增大，试件整体破坏历时缩短.

（3）在裂纹扩展前，即裂纹尖端累积能量阶段只有Ⅰ型应力强度因子产生，在裂纹开裂以后Ⅱ型应力强度因子才开始出现，裂纹开始出现张拉-剪切复合破坏，后期裂纹扩展中Ⅰ型应力强度因子占主导地位，裂纹主要受到拉应力影响.

（4）裂纹扩展速度在抵达层理面前，围绕某一数值震荡变化，到达层理后发生衰减，后期呈现总体降低的震荡变化.

（5）层理的参数会对介质的动态断裂产生影响.当弹性模量小于0.1 GPa时，裂纹在层理面中扩展的距离随弹性模量增大，但大于0.1 GPa时层理对有机玻璃的粘结作用增加，裂纹直接穿透层理.层理厚度增大时，裂纹沿层理弱面扩展的距离随之增大.

致谢

天津大学赵高峰教授对本文的数值模拟提供很大支持和帮助，在此表示感谢！