新型非对称惯容NES减震控制性能研究

刘志彬， 谭 平， 王菁菁， 陈洋洋

(1. 广州大学 土木工程学院，广州 510405； 2. 广州大学 广东省地震工程与应用技术重点实验室，广州 510405； 3. 广州大学 工程抗震减震与结构安全教育部重点实验室，广州 510405; 4. 广州大学 工程抗震研究中心，广州 510405)

结构振动控制技术可以有效抑制结构在风、地震等多种外部激励作用下产生的动力响应，按其控制方式的不同可分为被动控制、主动控制、半主动控制及混合控制[1]。结构控制技术能够有效减小地震响应，其中传统调谐质量阻尼器(tuned mass damper, TMD)仅在固定频率下发挥减震作用，非线性能量阱(nonlinear energy sink, NES)对能量变化的敏感性限制其控制能力的提升。学者为提高装置控制性能对TMD或NES进行深入研究：刘中坡等[2]通过对附加轨道型非线性能量阱的5层钢框架进行振动台试验，考察了该装置对建筑结构振动控制的效果；Wang等[3-5]在两种基础上提出几类将线性和非线性控制技术结合的联合控制技术，研究发现联合控制技术具有极强的频率鲁棒性和能量鲁棒性；刘良坤等[6]提出了一种非线性能量阱与调谐质量阻尼器混合控制结构振动的方案混合系统具有良好的鲁棒性，不仅拓宽了频带，而且降低了对初始能量的敏感性。

近年来一些基于惯容特性的新型耗能装置也相继提出，在建筑结构控制领域逐渐受到关注，其增效机制主要利用滚珠螺杆、齿条和齿轮等可以产生几十到数千倍于物理质量的表观质量[7]。英国学者 Smith[8]团队通过力学与电学间的力-电流类比，提出以“Inerter”(对应于电学中的电容)来命名两端点惯性元件，从理论角度概括了惯容元件(两端点惯性元件)的原理。与传统质量元件(单端点惯性元件)不同，惯容的出力与其两端点间的相对加速度相关(如图1所示)，其出力与两端相对加速度的比值称为惯容系数。

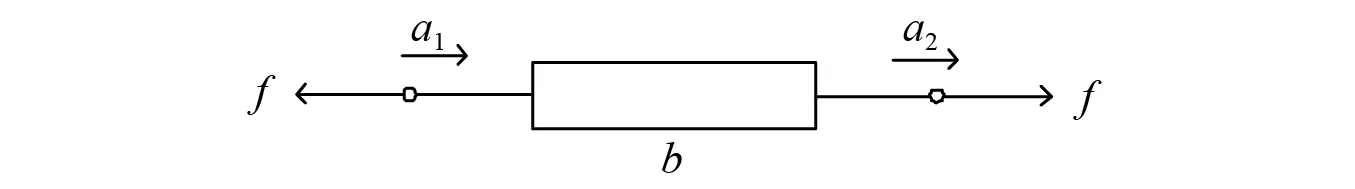
注： f为惯容力;b为惯容系数(量纲等同质量，也称惯容)；a1，a2分别为惯容两个端点的加速度。图1 两端点惯性元件—惯容Fig.1 Two-terminal inerter element—inerter

惯容与消能装置共同工作时能有效提高后者的能量耗散效率，这种耗能增益特性一方面源于惯容实现机制对等效黏滞系数的放大；另一方面是惯容-弹簧串联体系可以放大其内部自由度的变形[9]。20世纪70年代开始土木工程领域已经出现两端点的惯性机制的应用，Ikago等[10-12]将惯容机制引入旋转黏滞阻尼器，提出了一种新的控制装置—调谐黏滞质量阻尼器(tuned viscous mass damper, TVMD)。Marian等[13-15]在TMD体系加入惯容中，提出得调谐质量阻尼惯容器(tuned mass damper inerter, TMDI)的系统相对TMD在减小位移响应方面有明显优势。Ruiz等[16]通过响应分析对地震风险进行量化，并据此提出了一种TMDI的设计优化方法。张瑞甫[17]提出将惯容元件和阻尼元件串联(series viscous mass damper, SVMD)用于隔震结构，这与TVMD中黏滞元件与质量元件并联的连接方式不同。李壮壮等[18]提出了4种新型基于ISD结构的被动振动控制减振形式，以减少工程结构受到外部激励时的振动。赵志鹏等[19]提出一种非速度依赖型阻尼惯容系统，相较于传统的黏滞阻尼惯容系统提高耗能效率。上述研究均表明惯容与消能装置共同工作可以提高控制装置的减振性能，具有良好的工程应用前景。

基于上述研究，本文设计一种附加惯容器的非对称非线性能量阱(非对称NES[20])——非对称惯容NES，在脉冲型荷载作用下进行关键参数优化，并对地震激励下的响应规律进行研究。对各控制装置的位移响应进行小波分析，研究非对称惯容NES在宽频域上的减振机理，讨论非对称惯容NES在地震作用下的减震效果。

1 非对称惯容NES

设非线性弹簧组中弹簧刚度为k，弹簧原长为l，NES位移为x(如图2所示)。根据几何关系可得到非线性弹簧组在运动方向产生的恢复力为

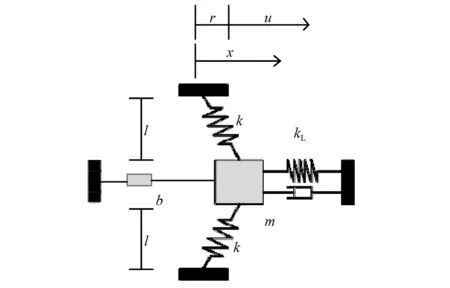
图2 非对称惯容NES示意图Fig.2 Schematic diagram of asymmetric inerter NES

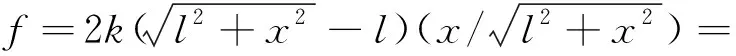
(1)

当NES位移小于弹簧原长时可省略高阶项，得到

f=kCubicx3

(2)

式中，kC为弹簧组非线性刚度，表达式为

kC=k/l2

(3)

当NES被拉离初始位置r时，非线性弹簧组恢复力为

fC(u)=kC(u+r)3

(4)

线性弹簧恢复力为

fL(u)=kLu+f0

(5)

式中，u为以r位置为参考的NES位移。

通过r位置的静力平衡条件，可以得到

fC(0)=fL(0)

(6)

f0=-kCr3

(7)

此装置设惯容系数为b，惯容力fb为

(8)

综合以上结果得到非对称惯容NES恢复力综合表现为

(9)

非对称惯容NES运动方程为

(10)

式中：m为滑动质量块质量；c为阻尼系数；xn为主体结构的顶层位移。图3是四种控制装置的恢复力-位移关系，可以看出非对称惯容NES和非对称NES同样具有非线性特性且相对NES对能量的变化不太敏感。

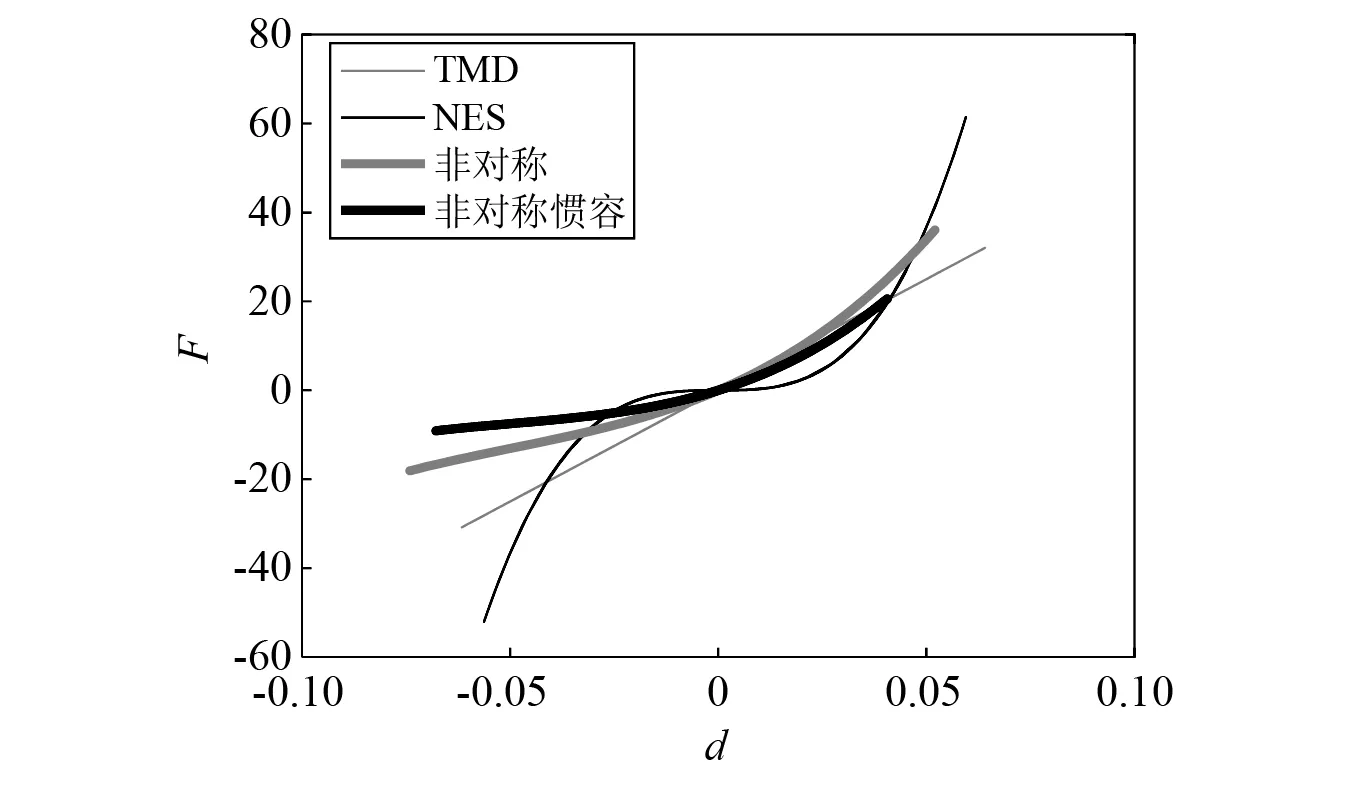
图3 TMD、NES、非对称和非对称惯容恢复力-位移关系Fig.3 Force-displacement relationships of TMD,NES,ASYM and ASYMI

2 控制参数优化

2.1 主体结构

本文中使用了某三层钢框架结构的两种不同刚度的模型作为主体结构，其动力特性已通过试验识别。该主体结构曾用于非对称NES的减震性能试验研究。图4(a)表示完好结构，每层由六片高弹性钢板柱连接。图4(b)表示损伤结构，每层由四片钢板柱连接。主体结构完好和结构破坏两种情况下是为了对比控制装置在不同主体结构刚度时减振性能的变化。表1识别得到的六柱和四柱主体结构各层质量和刚度，表2各阶阻尼比和自振频率。

图4 主体结构模型Fig.4 Physical realization of primary structure

表1 主体结构质量及刚度Tab.1 Mass and stiffness of primary structure

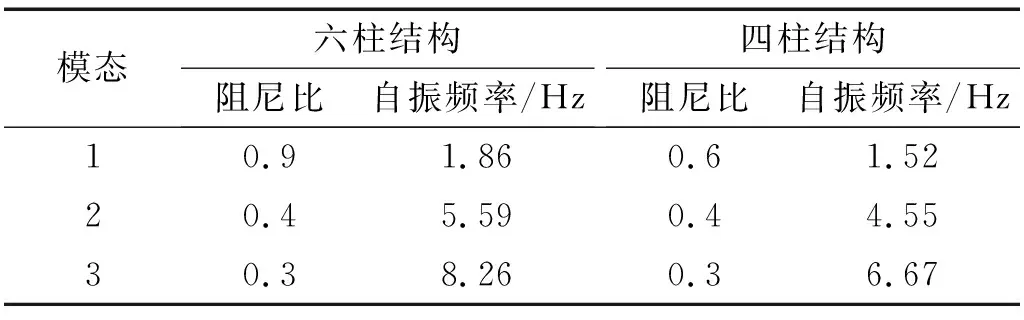
表2 主体结构阻尼比及自振频率Tab.2 Damping ratio and natural frequency of primary structure

2.2 参数优化

参数优化使用的主体结构为完好六柱结构。为方便后文各装置减振性能对比，本研究对TMD、一型NES、非对称非线性能量阱和非对称惯容NES分别进行了优化。其中TMD、一型NES和非对称NES控制装置质量比均取为主体结构质量的5%，为4.45 kg，非对称惯容NES的滑动质量取2.5%为2.225 kg，惯性元件质量考虑到后续试验实现的可能性取0.5 kg，非对称惯容NES附加质量相对其他控制装置减小约40%。两个优化控制参数为线性和非线性刚度系数。优化采用脉冲型荷载，通过对主体结构所有楼层和附加质量设置0.2 m/s的初始速度施加。优化目标为使15 s内主体结构顶层位移的均方根达到最小值。优化思路如图5所示，首先确定可能产生最佳减振性能的刚度系数的范围，然后通过模拟分析计算得到响应，根据响应分布调整刚度系数范围至同一数量级，最后确定最优参数取值。这种优化方法可以防止误取局部极值。

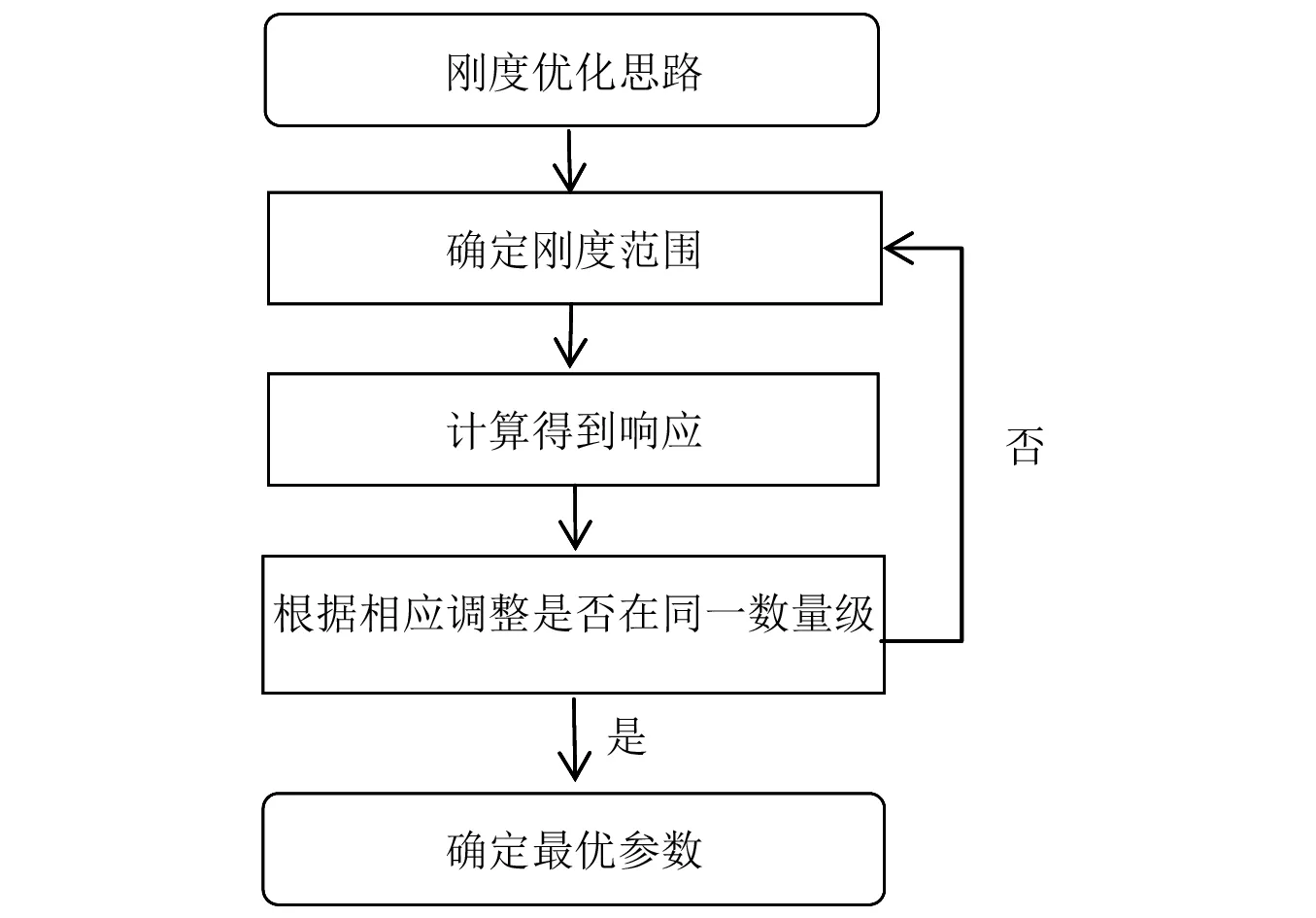
图5 刚度优化流程图Fig.5 Flow chart of stiffness optimization

TMD的待优化参数为刚度系数和阻尼系数，分别为500 N/m 和3.23 N·s/m。一型NES和非对称NES的阻尼系数 取值与TMD相同。一型NES的待优化参数为非线性刚度,优化结果为2.9×105N/m3。非对称NES的待优化参数为线性和非线性刚度。本文中平衡位置距离取为0.05 m，ASYM采用文献中优化好的刚度系数，非对称NES 线性和非线性刚度系数分别为190 N/m和2.8×104N/m3。非对称惯容NES是在非对称NES确定平衡位置距离的基础上进行参数优化。考虑到试验过程中惯容阻尼器的可行性，假定惯容阻尼器的质量b为0.5 kg，综合考虑非对称惯容NES在主体结构频率和能量变化时的表现，在此基础上优化的线性和非线性刚度系数分别为80 N/m和2.8×104N/m3(图6所示白色圆点)。

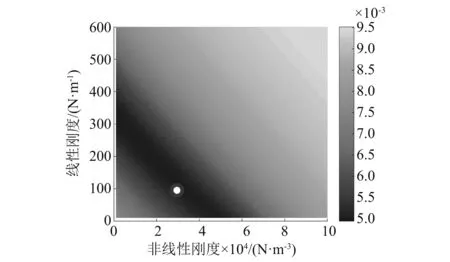
图6 非对称惯容NES刚度优化结果Fig.6 Optimization of asymmetric inerter NES

3 脉冲型响应分析

3.1 能量鲁棒性分析

图7对比主体结构为六柱时不同初始速度作用下无控系统、TMD系统、一型NES系统(图中简称NES)、非对称NES系统(图中简称非对称)以及非对称惯容NES系统(图中简称非对称惯容)的顶层位移响应。通过对比不同初始速度作用下各控制装置的减振性能可以发现，在优化荷载作用下各控制装置减振性能良好。

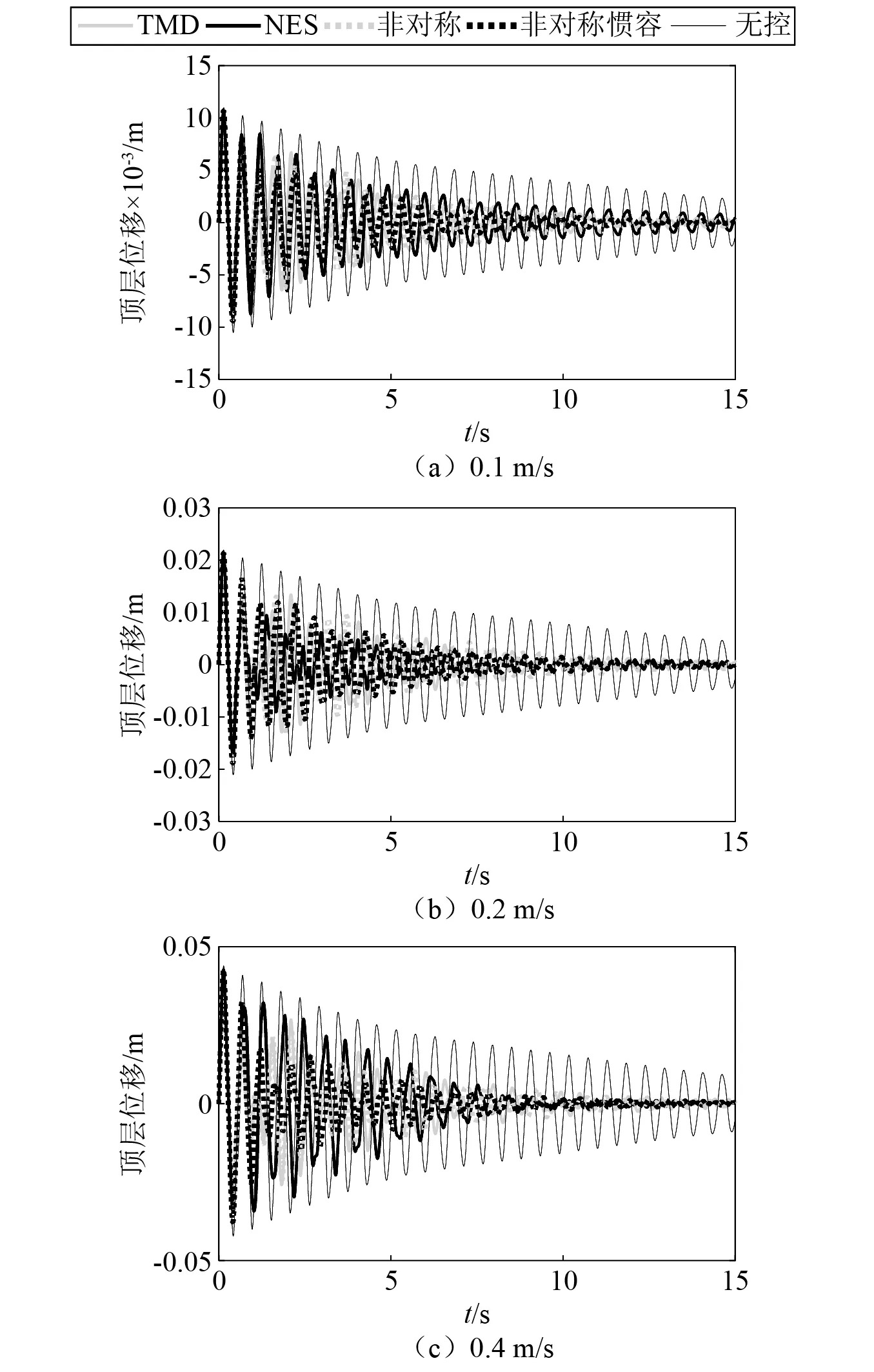
图7 六柱结构不同初始速度下顶层位移响应Fig.7 Top story displacements of original structure under various initial velocities

在荷载能量发生变化时，一型NES的减振效果较优化荷载的情况有了明显退化，与其他控制装置相比需要花费更长时间才能将主体结构位移减小至同一等级。TMD系统为线性系统，控制能力不因激励能量变化而改变，因此减振效率不发生变化。非对称NES系统和非对称惯容NES系统的控制效果与TMD系统十分接近，能量变化对控制性能的影响远小于一型NES。

3.2 频率鲁棒性分析

图8比较不同频率结构0.2 m/s 初始速度下顶层位移响应。通过观察时程曲线可以发现，当主体结构频率发生变化时， TMD调谐作用减弱，减振能力退化严重。NES、非对称系统和非对称惯容系统三种具有非线性恢复力特性的控制装置仍能保持较强的控制能力，展现了极强的频率鲁棒性。

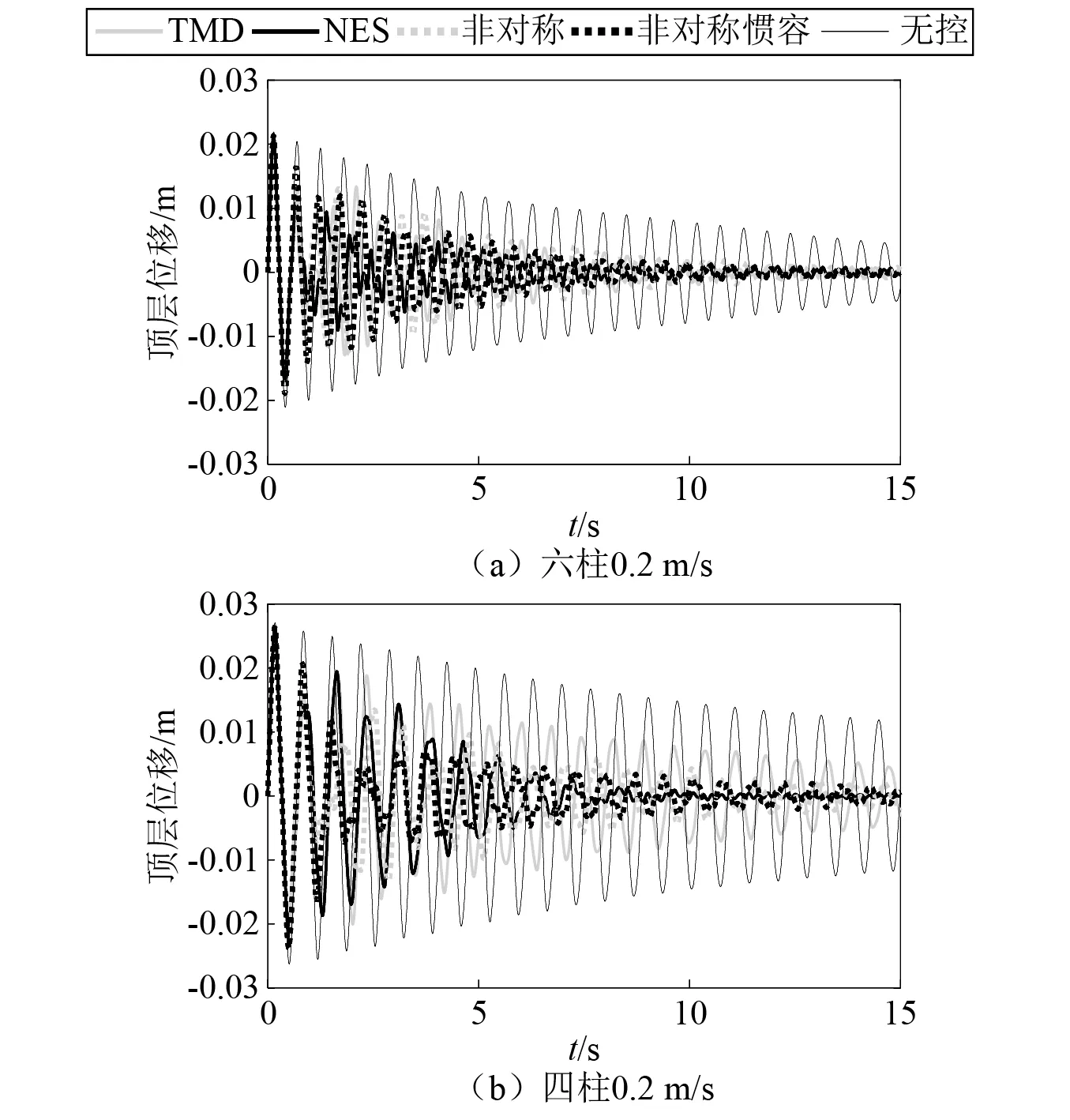
图8 不同频率结构0.2 m/s初始速度下顶层位移响应Fig.8 Top story displacements of under initial velocity of 0.2 m/s of structures with different frequencies

4 地震响应分析

4.1 地震记录

为考察新提出的新型非对称惯容NES在地震作用下的控制性能，本文对12条Kobe(1995年，7.2级)地震加速度作用下的结构响应进行了分析。表3列出了12条地震记录的信息，按照地面峰值加速度(peak ground acceleration,PGA)从小到大进行编号，PGA范围为0.33～3.41 m/s2。

表3 地震记录Tab.3 Seismic records

表4 12条地震作用下顶层加速度峰值及均方根均值Tab.4 Average value of peak and root mean square of top acceleration under 12 earthquake actions

表5 12条地震作用下顶层位移峰值及均方根均值Tab.5 Average value of peak and root mean square of top displacement under 12 earthquake actions

4.2 顶层加速度响应分析

图9列出主体结构为六柱时各控制系统在12条实测地震作用下与无控系统的顶层加速度峰值比值(见图9(a))和均方根比值(见图9(b))(具体数据见表A.1)。图9(a)可以发现在地震作用下，NES的加速度比值较大甚至超过无控结构加速度峰值，其他三种控制装置峰值均有一定程度减小。由于消能结构固有的延迟效应，峰值只比较时程中最大值，均方根对消能结构是更合理的评价指标。图9(b)对比了顶层加速度均方根，此时非对称惯容NES能将加速度均方根降低至50%以下，与TMD控制效果想当。图10展现了四柱结构时各控制装置在12条实测地震作用下与无控系统的顶层加速度峰值比值(见图10(a))和均方根比值(见图10(b))(具体数据见表A.2)。此时由于主体结构刚度发生变化，各控制装置控制能力都有一定的退化，NES由于对能量较敏感，对加速度峰值依旧没有较好的控制能力，ASYM与TMD也不能稳定的减小加速度峰值。非对称惯容NES相对其他三种控制装置能够有效减小加速度峰值，展现了较强的减震性能。

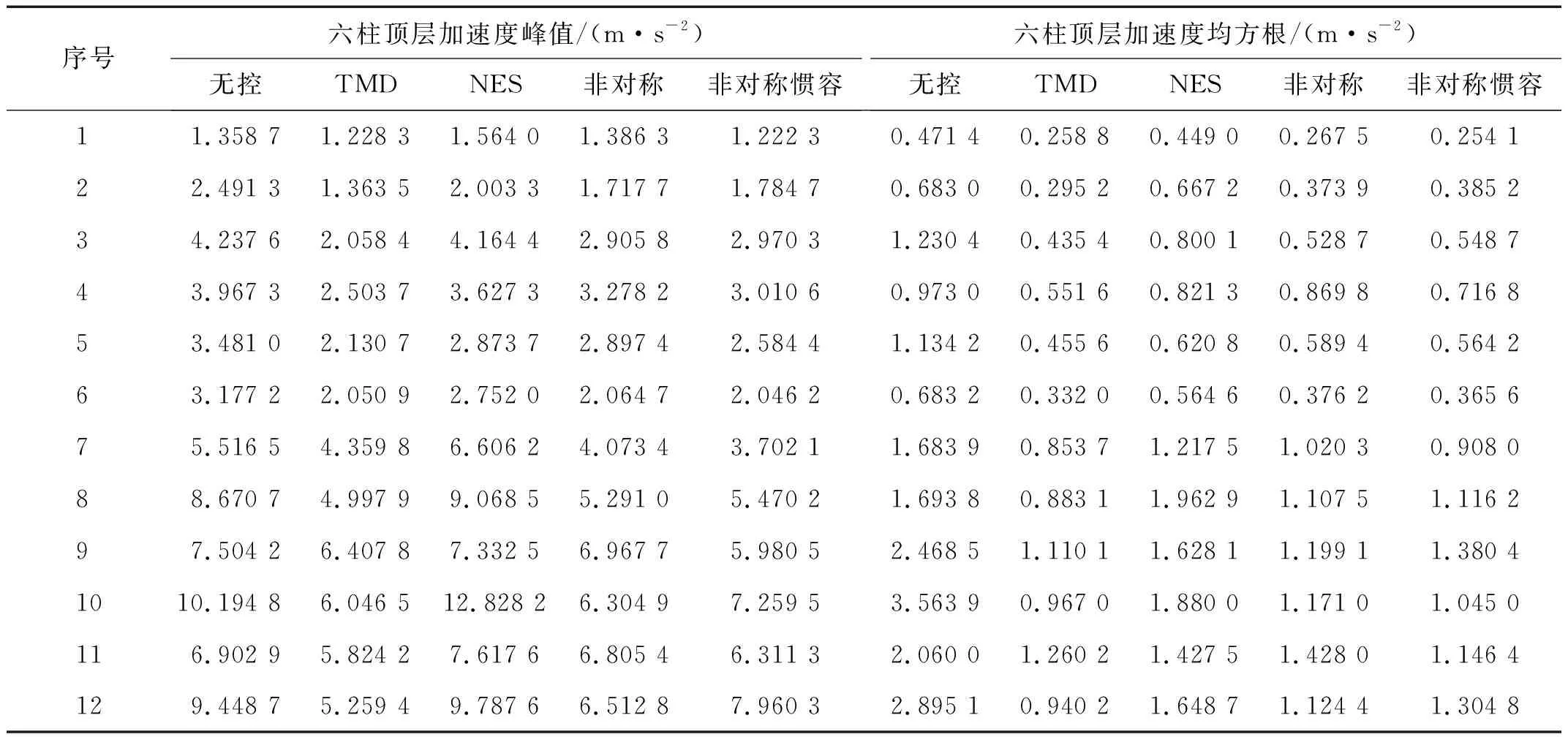
表A.1 地震作用下六柱结构顶层加速度峰值及加速度均方根Tab.A.1 Peak and root mean square of top acceleration of six columns under 12 earthquake actions

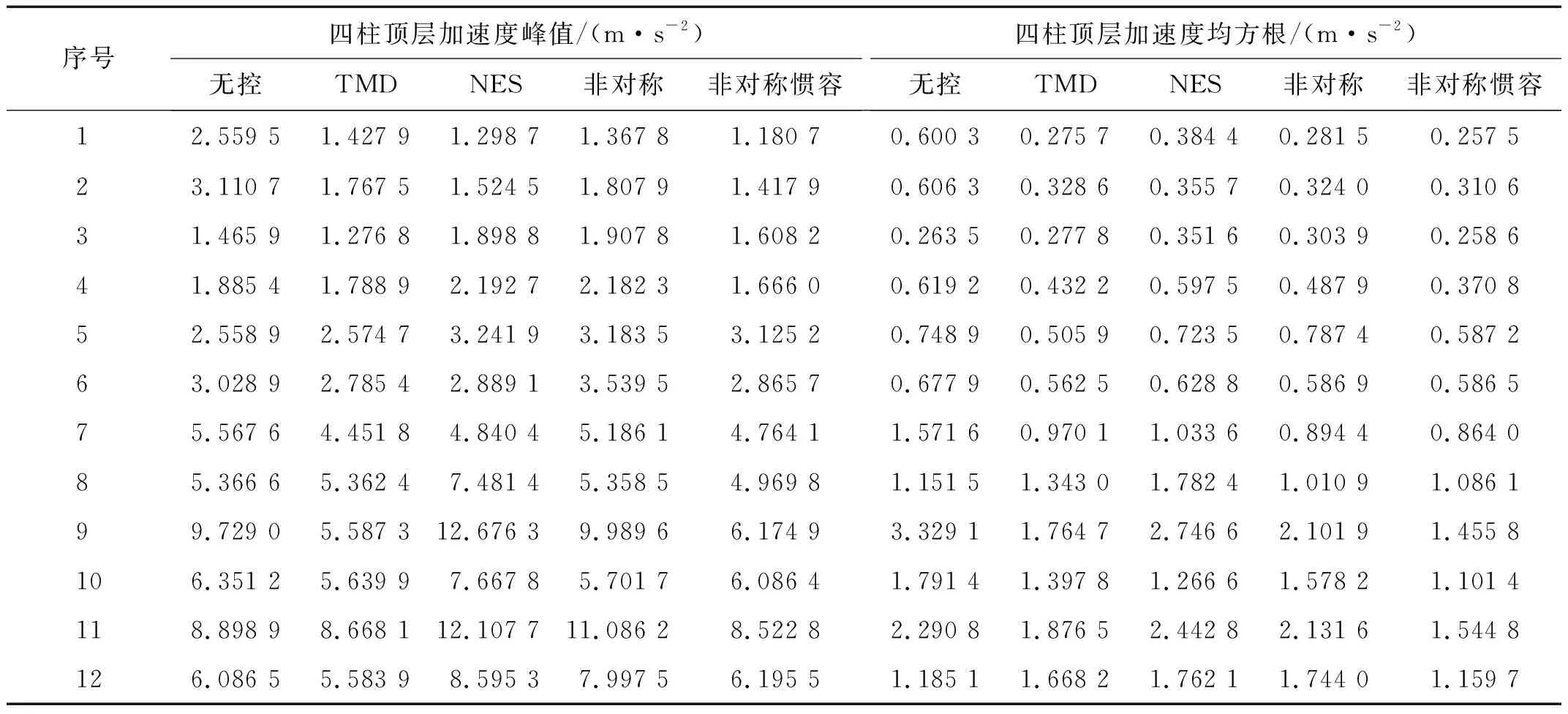
表A.2 地震作用下四柱结构顶层加速度峰值及加速度均方根Tab.A.2 Peak and root mean square of top acceleration of four columns under 12 earthquake actions

图9 六柱结构12条地震作用下顶层加速度峰值比值和均方根比值Fig.9 Peak ratio and root mean square ratio of top acceleration under 12 earthquake actions of original structure

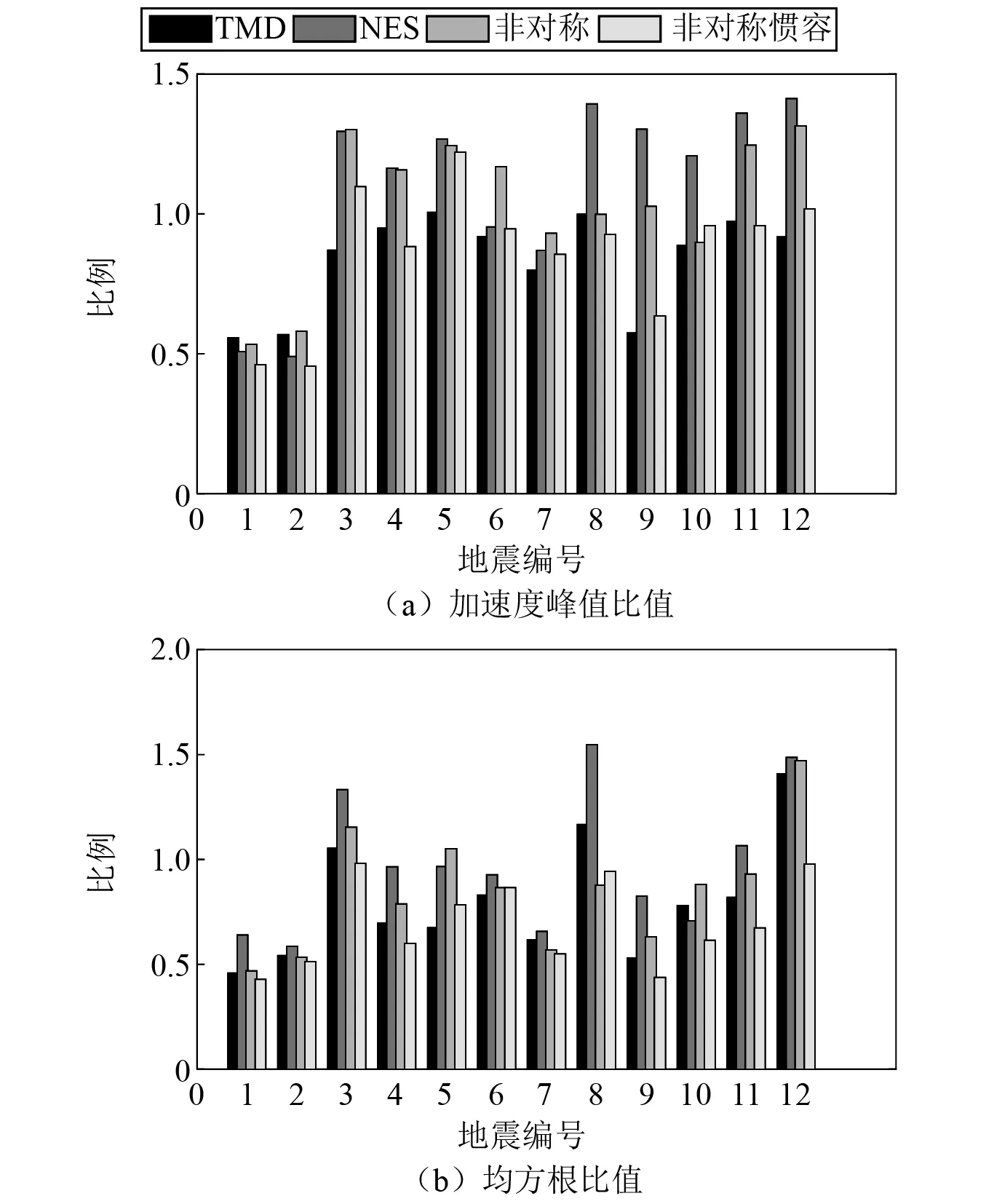
图10 四柱结构12条地震作用下顶层加速度峰值比值和均方根比值Fig.10 Peak ratio and root mean square ratio of top acceleration under 12 earthquake actions of damaged structure

4.3 顶层位移响应分析

图11列出主体结构为完好六柱结构时各控制装置在12条实测地震作用下与无控系统的顶层位移均方根比值(具体数据见表A.3)。可以发现在地震作用下，由于地震能量的随机性，NES的控制性能较弱，其他三种控制装置减振能力相当，顶层位移均方根比值均能保持在50%以下。图12列出主体结构四柱结构时各控制装置在12条实测地震作用下与无控系统的顶层位移均方根比值(具体数据见表A.4)。此时由于主体结构刚度发生变化，各控制装置控制能力都有一定的退化，尤其NES与TMD退化严重。此时非对称惯容NES具有极强的频率鲁棒性和能量鲁棒性，在具有随机能量的地震动的作用下能够保持较强的减振性能。

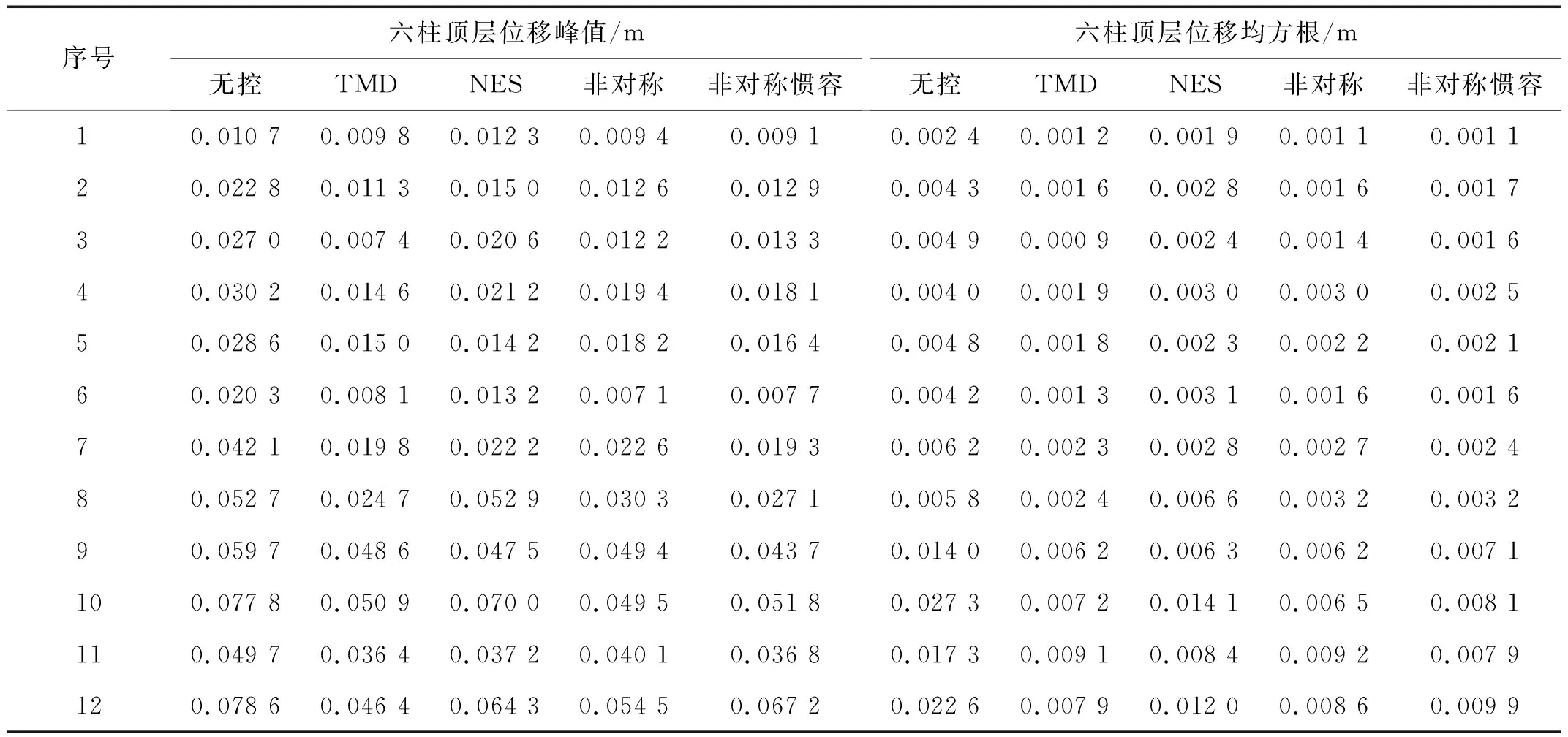
表A.3 地震作用下六柱结构顶层位移峰值及加速度均方根Tab.A.3 Peak and root mean square of top displacement of six columns under 12 earthquake actions

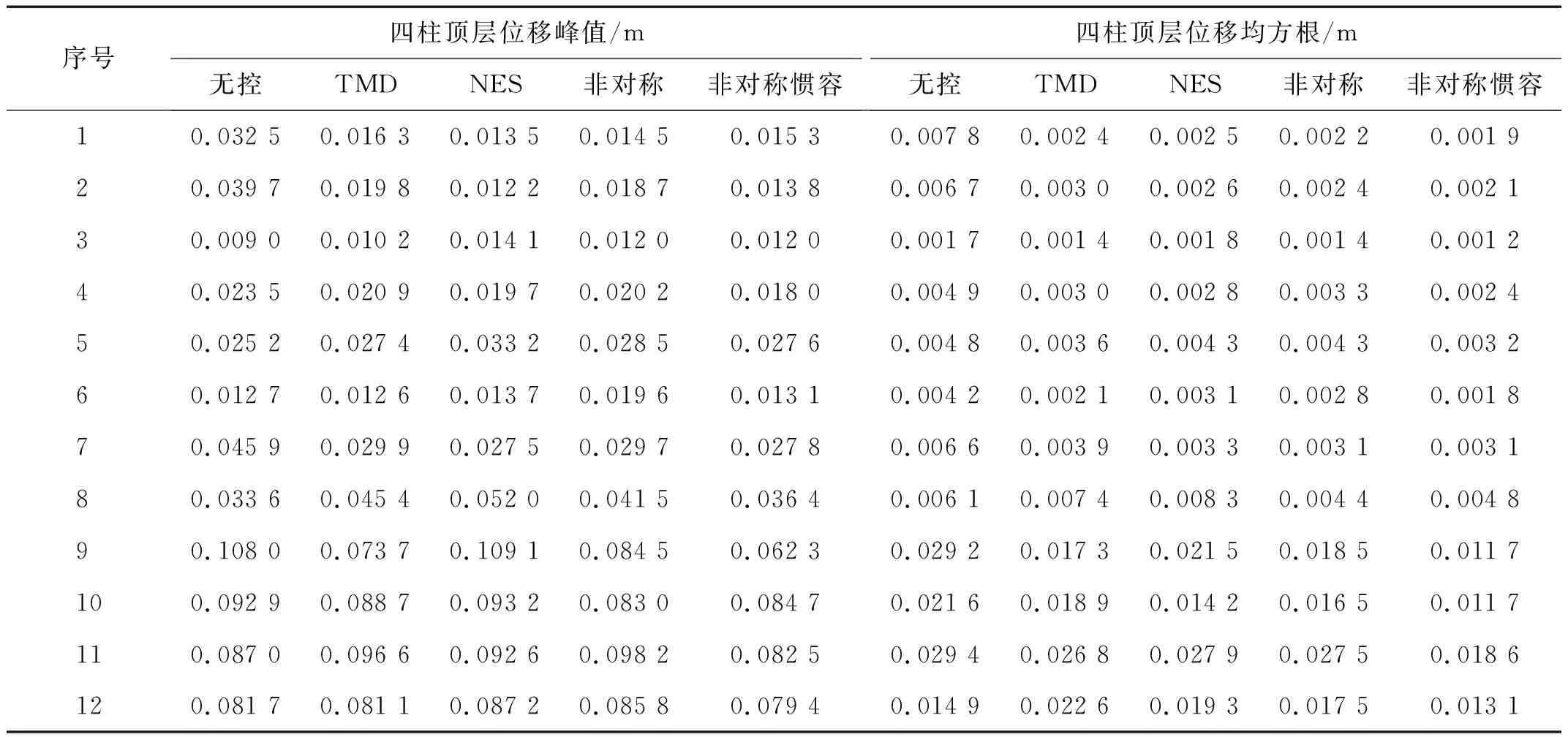
表A.4 地震作用下四柱结构顶层位移峰值及加速度均方根Tab.A.4 Peak and root mean square of top displacement of four columns under 12 earthquake actions

图13、图14列出了主结构为六柱和四柱时的11号地震动作用下的结构位移响应时程。图13显示了六柱完好结构在地震作用下的位移响应时程，可以发现四种控制装置都能快速耗散能量，在极短时间内减小顶层位移。图14列出了四柱损伤结构各控制系统在地震作用下的减震能力，由于TMD与主体结构不再调谐，减震能力弱化严重。NES和非对称NES控制能力也有一定的退化，但非对称惯容NES能够在主体结构刚度变化时保持较强的控制能力，具有极强的频率鲁棒性和能量鲁棒性。所反映的情况与图11、图12的结论是一致的。

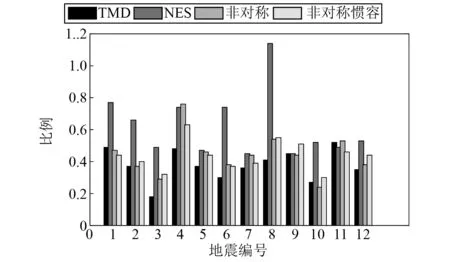
图11 六柱结构12条地震作用下顶层位移均方根比值Fig.11 Root mean square ratio of top displacement under 12 earthquake actions of original structure

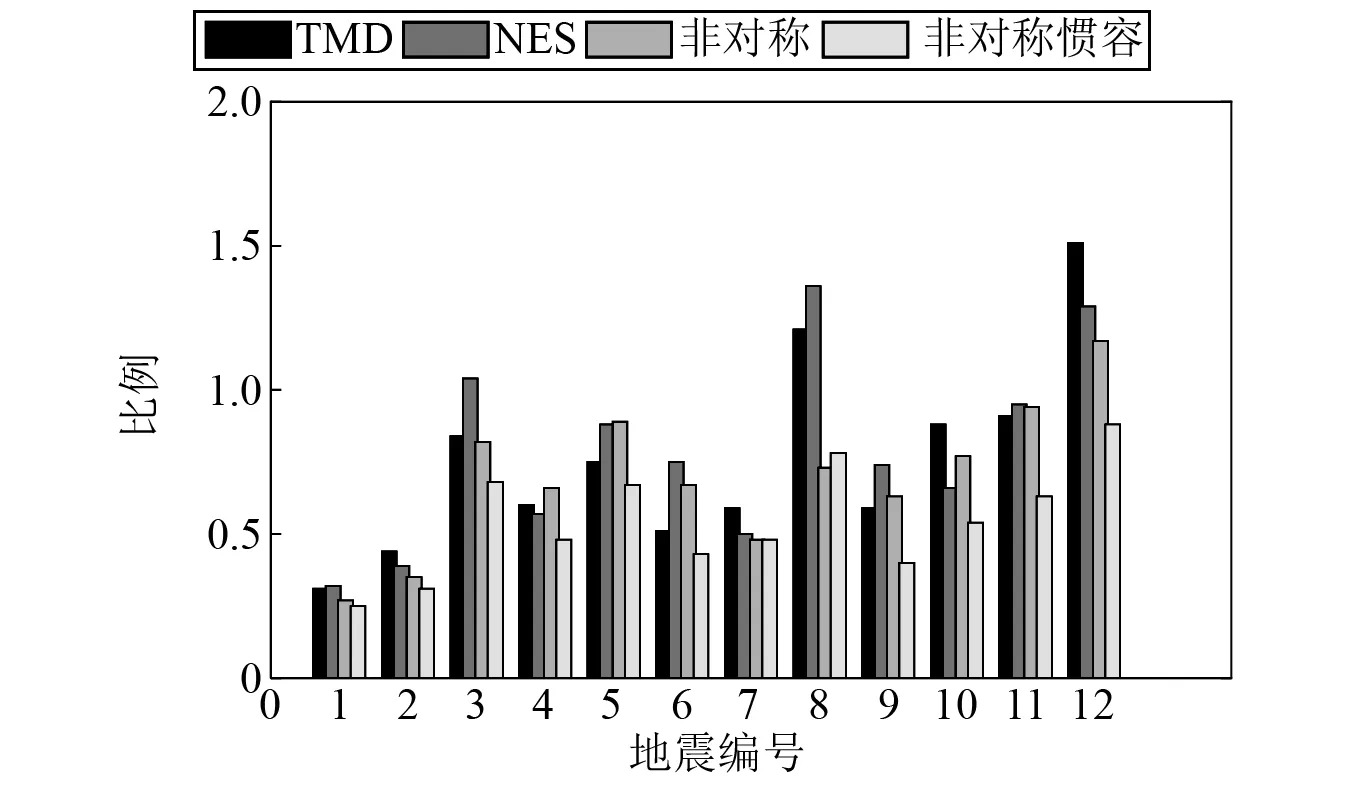
图12 四柱结构12条地震作用下各控制装置顶层位移均方根比值Fig.12 Root mean square ratio of top displacement under 11 earthquake actions of damaged structure

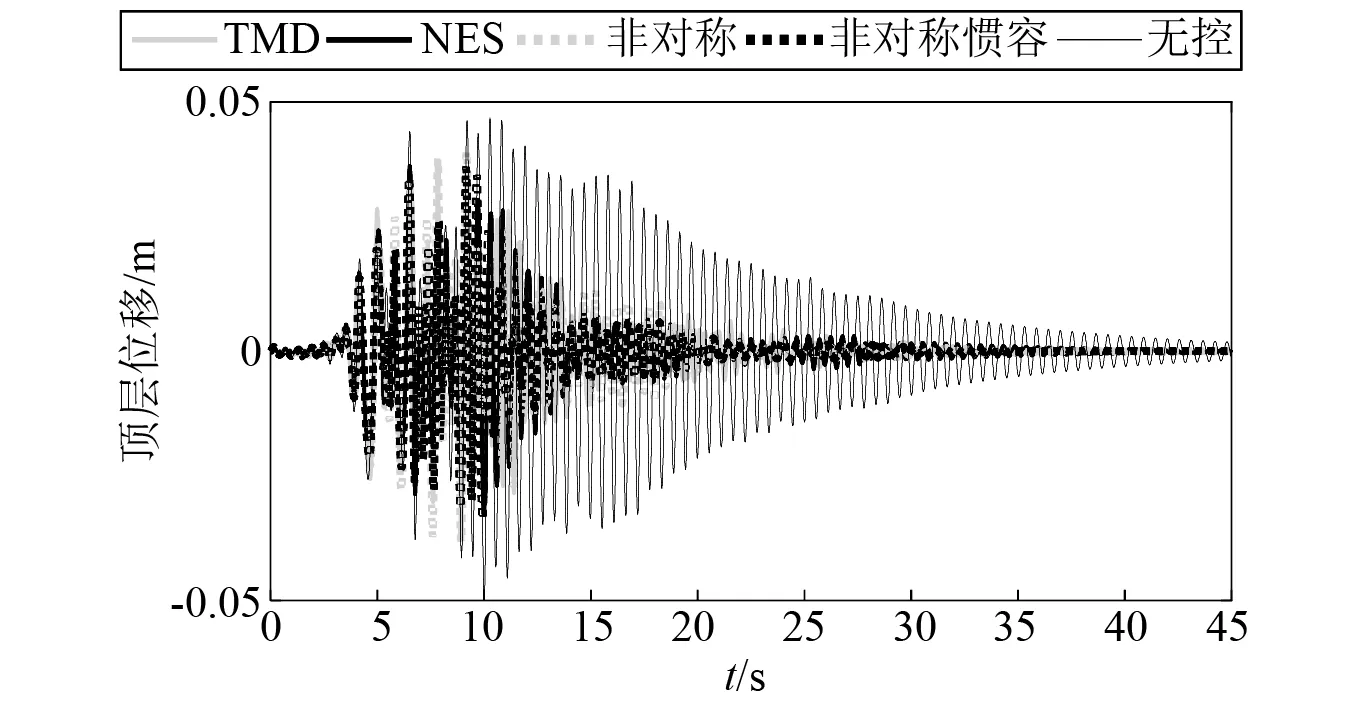
图13 六柱结构11号地震作用下顶层位移响应时程Fig.13 Top floor displacement response of original structure under No.11 earthquake

图14 四柱结构11号地震作用下顶层位移响应时程Fig.14 Top floor displacement response of damaged structure under No.11 earthquake

5 小波分析

为观察主结构与子结构之间的能量传递，对主结构与附加子结构的响应进行小波分析。采用此方法对12条Kobe(1995年，7.2级)实测地震加速度激励下的位移响应进行分析，图15和图16显示了在代表性11号地震动作用下不同主体结构响应的小波功率谱，并标出主体结构的基频以观察能量响应的频率分布。

主结构无控情况下的基频(1.86 Hz)图15 六柱结构11号地震动记录作用下的位移响应小波功率谱Fig.15 Numerical wavelet transform spectrum for displacement response of original structure under No.11 seismic record

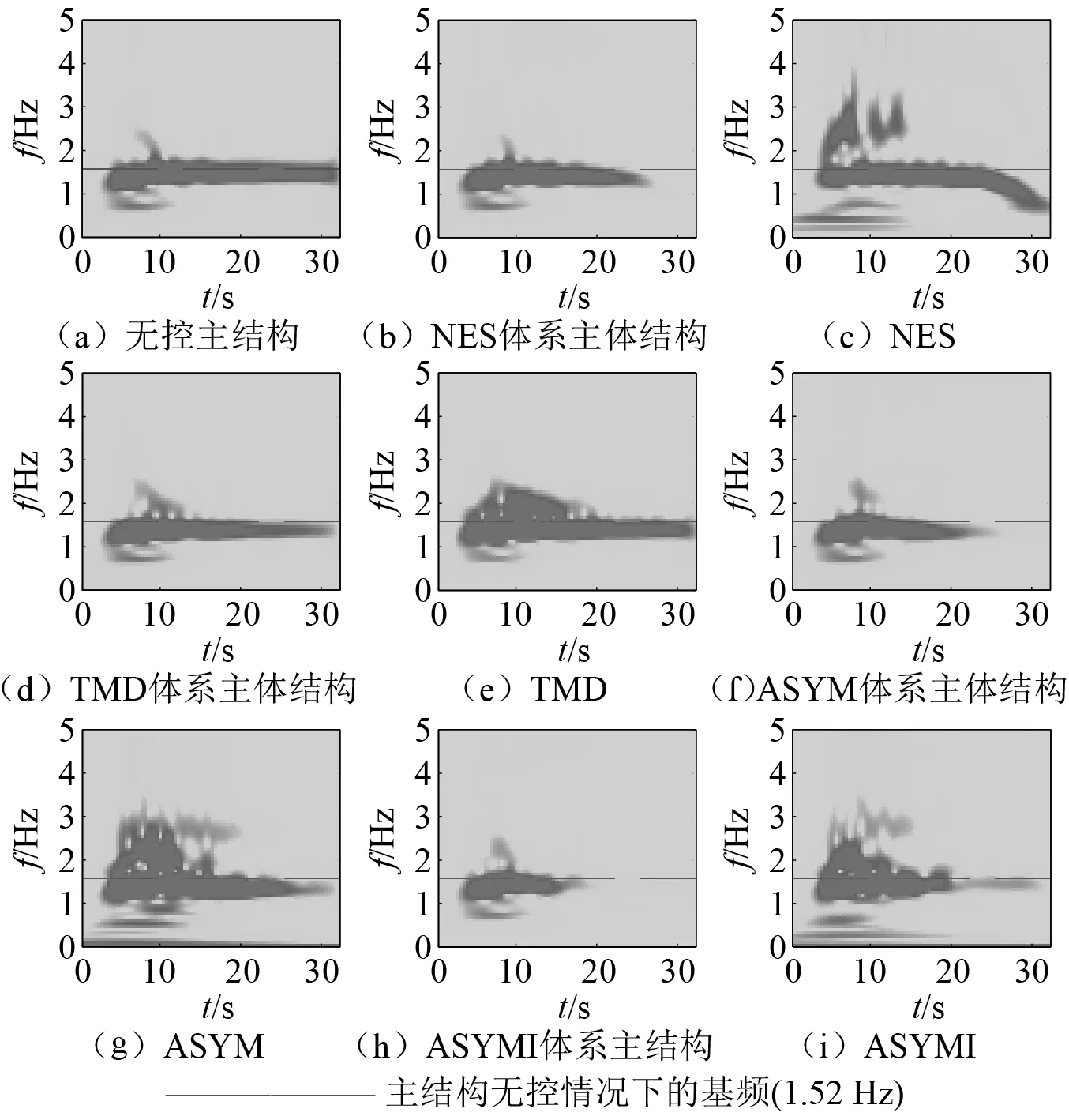
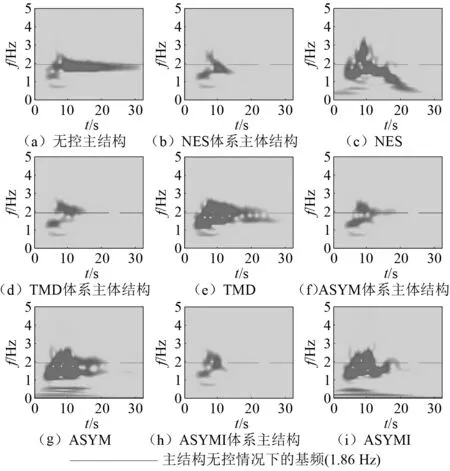
主结构无控情况下的基频(1.52 Hz)图16 四柱结构11号地震动记录作用下的位移响应小波功率谱Fig.16 Numerical wavelet transform spectrum for displacement response of damaged structure under No.11 seismic record

图15(a)是无控主结构的小波功率谱，尽管地震动频带较宽，但无控结构的响应能量仍然大部分集中在基频1.86 Hz附近，只能通过自身阻尼耗能，符合典型线弹性无控结构的响应特点。图15(b)和图15(c)给出相应的一型NES体系响应情况，一型NES不再局限在主结构基频附近能够在更广频域内快速耗能，主体结构的响应也能快速减小。图15(d)和图15(e)描述了TMD体系的响应情况，可以看到，子结构和主结构的响应频率基本一致，都集中在基频附近，表明TMD能够在短时间内耗散主体结构能量，符合TMD系统的特点。图15(f)和图15(g)描绘了非对称NES体系的响应情况，可以发现，该控制装置能够在极短时间内降低主体结构响应，并响应能量分布在更广的频域上。图15(h)和图15(i)描绘了非对称惯容NES体系的响应情况，可以看到，非对称惯容NES能够在极短时间内耗散主体结构能量，且能在较宽频域内发挥作用。

图16给出了11号地震动作用下主结构为四柱结构时位移响应的小波功率谱，此时无控主结构的基频为1.52 Hz。各控制装置由于基频的改变使主结构的能量衰减变慢，TMD系统与主体结构不再调谐，NES控制能力由于地震能量的随机性也降低，减振性能都有所降低。但非对称NES和非对称惯容NES中特别是非对称惯容NES仍能够在短时间内消耗主结构能量，这表明对非对称NES和非对称惯容NES特别是非对称惯容NES影响相对不大，是其表现出更强减震能力的原因。我们对其余11条地震加速度激励作用下响应时程的进行小波分析，可以总结出相似的结论。

6 结 论

基于非对称NES设计一种附加惯容器的新型控制方法——非对称惯容NES，它是具有NES特性的被动结构控制装置。非对称惯容NES是在非对称NES的基础上开发的，它在辅助质量和定点之间添加了惯容器，可以看作是非对称NES的推广，相对在非对称NES质量减小约40%。在三层钢结构模型中进行关键参数优化和数值模拟分析，最后在12条实测地震动记录作用下的进行响应分析，进一步展现了非对称惯容NES的优势。主要结论总结如下：

(1) 非对称惯容NES在脉冲型荷载作用下优化的参数在能量和频率改变时展现出极强的减振性能，说明考虑结构性质和能量变化的非对称惯容NES具有良好的控制性能。

(2) 在地震作用过程中，非对称惯容NES能够有效减小主体结构顶层加速度峰值并能在极短时间减小主体结构顶层位移；在主体结构刚度变化前后仍旧保持良好的控制能力。

(3) 对代表性的11号地震动作用下结构响应进行小波分析，非对称惯容NES能在更广频域内与主体结构发生共振，主体结构刚度变化前后对非对称惯容NES的内共振俘获行为影响不大，能够保持较强的减震能力。对其余11条地震作用下结构响应时程的小波功率谱进行分析，可以总结出相似的结论。