粗糙表面微凸体模型构建与接触特性分析

李 玲， 何本帅， 王晶晶， 张锦华， 蔡安江

(西安建筑科技大学 机电工程学院，西安 710055)

机械结合面之间的接触在微观层面上是两个粗糙表面间的接触问题。相互接触的粗糙表面在机械系统运行过程中起着传递运动、负载和能量的重要角色，其接触行为直接关系到机械零件之间的连接性能，对机械系统的静态和动态行为都有着重要的影响[1-4]。因此，准确地构建粗糙表面间的接触模型，开展粗糙表面的接触特性研究，对于现实机械工程问题的解决具有重要意义。

为了研究粗糙表面的接触特性，很多学者在接触力学领域不断创新。Greenwood等[5]基于统计学理论，将粗糙表面上的微凸体高度分布看成随机函数，最先提出粗糙表面的弹性接触模型，即GW模型。后来,许多学者开始拓展GW模型，并提出了许多全新的模型。例如：Chang等[6]基于微凸体在塑性变形阶段的体积守恒原理，提出了一种微凸体塑性接触模型，并将两者拟合获得了弹塑性接触特性，利用统计学理论获得了整个粗糙表面的接触模型，简称CEB模型；Zhao等[7]为了研究微凸体从弹性变形阶段向塑性变形阶段转变的力学过程，基于接触力学理论，利用数学多项式将微凸体的弹性行为和完全塑性行为紧密联系起来，获得了微凸体在三种变形阶段的接触特性曲线，简称ZMC模型；Kogut等[8]通过有限元方法深入研究了单个球体与刚性平面的接触行为，并使用幂函数公式拟合获得了弹性、弹塑性和完全塑性状态下接触载荷与变形量之间的解析表达式，简称KE模型；Jackson等[9]利用有限元的方法，研究了微凸体在变形过程中材料属性和几何形状的影响，简称JG模型。国内学者[10-12]对结合面的力学模型也进行了研究和分析，促进了粗糙表面接触特性的研究和发展。

上述学者对于粗糙表面的接触特性研究重点放在了接触力学部分，所采用的微凸体轮廓假设与GW模型相同，均为半球体模型，并未涉及微凸体模型的重新建立。但国外学者[13-15]对粗糙表面的测量研究发现，正弦形接触比半球形接触能更好地模拟粗糙表面的微凸体接触，并将粗糙表面转换成傅里叶级数或魏尔斯特拉斯曲线来考虑多尺度的微凸体，重新建立粗糙表面接触模型。同时，国内学者安琪等[16]针对磨削表面的微凸体轮廓，提出一种半周期余弦曲线回转体模拟磨削表面微凸体的接触模型；Shang等[17]提出一种采用抛物线回转体等效微凸体的方法，推导出粗糙表面法向刚度与弹性接触之间的理论关系。随着这类模型广泛应用于粗糙表面的接触特性研究，如何更加合理地优化粗糙表面的接触模型具有重要意义。

本文基于粗糙表面形貌测量试验，提出一种采用二次函数回转体等效微凸体的办法，建立微凸体接触半径与接触变形的解析关系。然后根据几何模型，重新推导出单个微凸体在弹性、弹塑性和完全塑性三种变形阶段的接触表达式，并应用接触力学理论和概率统计方法，建立粗糙表面的微观接触模型。最后针对模型的有效性进行了验证和分析，并揭示了塑性指数、微凸体尺寸参数对接触特性的影响规律。

1 粗糙表面模型构建

1.1 粗糙表面形貌测量试验

本文使用Talysurf非接触式光学轮廓仪测量表面形貌，获取不同加工工艺下的二维表面信号。利用频谱分析法确定表面成分有效信息的频段范围，并把不同频率成分的信息分解到互不重叠的频段上，获得试块表面的粗糙度以及二维轮廓曲线数据。图1为表面形貌测量试验。图1(a)为合金钢长方体试块，上表面为待测表面，待测表面区域为20 mm×20 mm，材料为20CrMo。在前立面上作有标记，为了便于说明，将打标立面与上表面的交边记为参考线。图1(b)为测量位置，每个表面分3次测量，如图1(b)中所标的1，2和3等三条线段，测量时由下向上，测试长度选取3 mm左右，最小采样间距为0.25 μm。

图1 粗糙表面形貌测量试验Fig.1 Rough surface morphology measurement experiment

试验共选取三种不同加工工艺的待测表面，分别为：①Ra=0.85 μm，磨削+热处理加工表面；②Ra=1.302 μm，磨削加工表面；③Ra=1.602 μm，铣削加工表面。将获得的表面二维轮廓曲线数据进行整理，每个测试表面选取一组数据，使用MATLAB软件仿真，获得不同粗糙表面的二维轮廓，如图2所示。

图2 不同粗糙表面的二维轮廓Fig.2 Two-dimensional profile of different rough surfaces

由图2可知，不同加工工艺下的粗糙表面在微观层面上均是粗糙不平的，随机分布着许多大小不一的凹谷和凸峰，其二维轮廓曲线差异较大。从局部放大图可以看出，虽然各表面的粗糙度和加工工艺不同，但单个微凸体的二维轮廓曲线，均呈现出顶部较窄，底部较宽的特征，与二次函数曲线具有很高的相似度。

1.2 单个微凸体的轮廓模型

单个微凸体的二维轮廓特征与二次函数曲线具有很高的相似度，据此微凸体的二维轮廓可用二次函数曲线进行假设，如图3所示，l为微凸体的直径，h为微凸体的高度。

图3 微凸体二维轮廓模型假设Fig.3 Assumptions of the 2D profile model of asperities

根据图3，可定义粗糙表面上单个微凸体的二维几何尺寸为

(1)

式中，x的范围为微凸体正负直径的一半。参数l和h的获取方法为：首先，分别对粗糙表面微凸体轮廓的凸峰值与凹谷值进行标记；然后，对所标记的相邻峰值点的间隔进行求和，得到相邻峰值点间距的平均值的一半作为微凸体的直径l；对所标记的相邻峰谷值做差处理，进而得到各峰谷差值的平均值作为微凸体的高度h。

根据测量表面的二维轮廓数据，随机选取单个微凸体的数据点，通过对比二次函数模型和半球体模型的拟合效果，来验证二次函数模型的正确性，如图4所示。从整体来看，二次函数拟合曲线与实测数据更吻合，尤其是在微凸体底部。半球体模型无法实现完全拟合的原因是采用单一的曲率半径，在重载的情况下会对单个微凸体的解析计算带来误差。值得注意的是，半球体模型的拟合曲线呈现出半椭圆形态是因为轮廓数据点的水平方向和垂直方向的放大比率不同，产生了畸变现象。本文提出的二次函数模型实现了对微凸体整体轮廓的拟合，能够在载荷较大的情况下，更加精确地进行结合面接触特性分析。

图4 微凸体二维轮廓拟合验证Fig.4 Two-dimensional contour fitting verification of asperity

综上所述，微凸体的二维轮廓采用二次函数曲线拟合。对于微凸体的三维轮廓，可通过二次函数曲线沿着z轴旋转一周获得的回转体模型进行表征。与半球体模型的建立类似，本文模型基于以下假设：①将两粗糙表面之间的接触等效为一刚性平面与一等效粗糙表面的接触；②微观接触表面的微凸体轮廓为二次函数回转体，其高度分布符合高斯分布；③在接触变形过程中只考虑微凸体变形，宏观基体变形和微凸体之间的相互作用不予考虑。

2 粗糙表面理论建模

2.1 单个微凸体的微观接触

图5为单个微凸体与刚性平面之间的接触原理。图5中：d为接触间隙；r为接触半径；δ=h-d为接触变形。

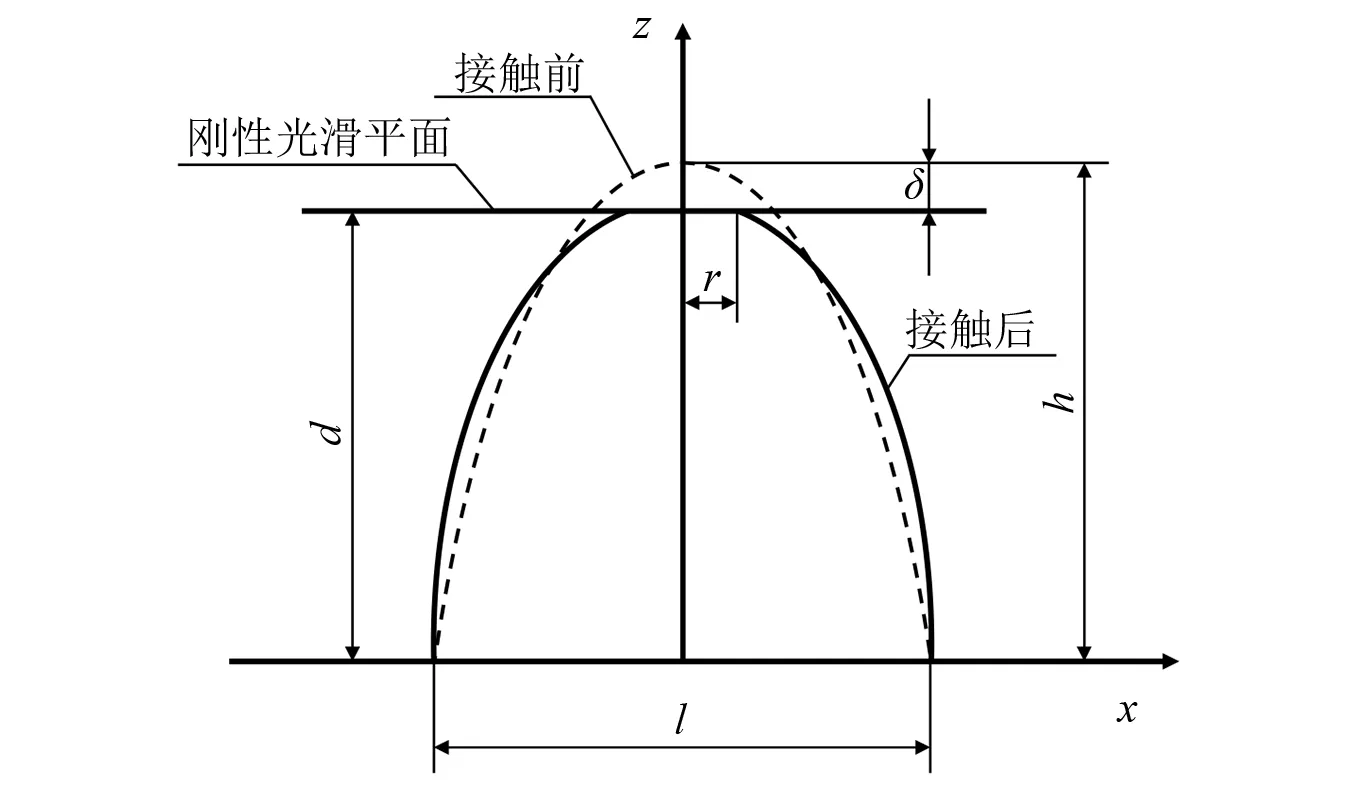
注：虚线表示微凸体的初始形状；实线表示施加载荷发生接触变形后的形状。图5 单个微凸体微观接触模型Fig.5 Micro-contact model of single asperity

结合图5与式(1)，可得单个微凸体的接触半径r与接触变形δ的关系为

(2)

随着接触载荷的逐步增大，接触变形δ和接触半径r也将随之增大。当接触载荷逐渐增大到超过材料的屈服极限时，微凸体的变形将逐渐由弹性向弹塑性并最终向完全塑性转化，下面将分阶段对微凸体的变形过程进行分析。

2.1.1 弹性变形阶段

当δ<δc，接触变形较小时，微凸体处于弹性变形阶段，可视为一个等效曲率半径为R的半球体与刚性平面的弹性接触，这与半球体模型假设类似。因此，微凸体顶端可采用HERTZ接触理论[18]的处理办法，求得弹性变形阶段的平均接触压力pe的表达式为

(3)

根据Tabor[19]的研究结论，在最大HERTZ压力等于0.6H，即pe=0.4H时微凸体开始出现塑性变形。对于一般的情况，开始出现塑性变形的条件为

(4)

式中：k为最大平均接触压力的系数，k=0.454+0.41v，v为较软材料的泊松比；H为较软材料的硬度。

将式(4)代入式(3)，可推导出材料初始塑性屈服点的临界变形量δc为

(5)

根据二次函数回转体模型，求得微凸体顶点轮廓线的曲率半径re为

(6)

根据HERTZ接触理论进行推导，将半球体模型的等效曲率半径R用二次函数回转体模型的顶点轮廓线曲率半径re代替，进而弹性变形阶段的接触面积ae的表达式为

(7)

结合式(3)和式(7)，整理可得弹性变形阶段接触载荷fe的表达式为

(8)

由式(8)可得，弹性变形阶段接触刚度ke的表达式为

(9)

2.1.2 完全塑性变形阶段

当δ>δp时，微凸体将发生完全塑性变形。δp为材料在完全塑性屈服临界点对应的变形量，δp=tδc。根据文献[20-21]的研究，选择比率t=110。在这个阶段，平均接触压力pp为较软材料的硬度[22]，是一个定值，即

pp=H

(10)

在回转体模型接触区域近似圆形的情况下，可根据Johnson[23]的研究将完全塑性变形阶段的接触面积ap表示为

(11)

式中，rp为完全塑性变形阶段微凸体的接触半径。

结合式(10)和式(11)，完全塑性变形阶段接触载荷fp的表达式为

(12)

由式(12)可得，完全塑性变形阶段接触刚度kp的表达式为

(13)

2.1.3 弹塑性变形阶段

当δc<δ<δp时，微凸体既发生弹性变形，也发生塑性变形，平均接触压力与接触变形的关系将变得极为复杂，无法进行准确的定量描述。采用改进的HERMIT多项式插值方法[24]进行过渡处理，增强平均接触压力在弹塑性变形始末的连续性和光滑性，其表达式为

(14)

根据文献[25]的方法，弹塑性变形阶段的接触面积aep可通过构建样板函数，实现其在弹塑性变形始末的连续、光滑和单调性要求，表达式为

(15)

式中，C1和C2分别为二次项系数和三次项系数，且同时满足以下条件

(16)

将式(18)代入式(17)中，可得

(17)

根据式(14)和式(15)推导出弹塑性变形阶段接触载荷fep的表达式为

(18)

由式(18)可得，弹塑性变形阶段接触刚度kep的表达式为

(19)

2.2 粗糙表面之间的微观接触

两个粗糙表面在接触过程中，有如下定义：名义接触面积An上如果有N个微凸体，则所有接触的微凸体数目可以表示为

(20)

式中：d为给定的接触表面平均距离；η为微凸体的面积密度；An为名义接触面积；Ф(z)为微凸体高度分布的概率密度函数，其表达式为[26]

(21)

(22)

2.2.1 弹性变形阶段

(23)

(24)

(25)

2.2.2 弹塑性变形阶段

(26)

(27)

(28)

2.2.3 完全塑性变形阶段

(29)

(30)

(31)

整个粗糙表面的接触面积、接触载荷和接触刚度分别是所有接触的微凸体在三个变形阶段的累加和。且为了确保所得到的结果具有广泛适用性，分别用An，EAn和σ/EAn对上述接触参数进行无量纲处理，获得无量纲接触面积A*、无量纲接触载荷F*和无量纲接触刚度K*的表达式，即

(32)

(33)

(34)

3 模型验证

为验证所建模型的有效性，基于图2中粗糙表面(Ra=1.302 μm)的实测数据，材料弹性模量E1=E2=211 GPa，泊松比v1=v2=0.28，材料硬度H=1.96 GPa，微凸体的直径l=16.790 μm，微凸体的高度h=1.082 μm。选取表1中[27]的塑性指数ψ=2.0，根据式(6)求得σ=0.037 μm，η=4.459×1010m-2，进行模型验证。

表1 不同塑性指数的表面参数Tab.1 Surface parameters for different plasticity indices

3.1 单个微凸体接触模型对比验证

图6为单个微凸体接触面积a、接触载荷f分别与变形量的关系，比较了本文模型与CEB模型、ZMC模型和KE模型的预测结果。如图6所示，本文模型的曲线均呈现连续光滑地变化趋势，且与对比模型的趋势是一致的。随着变形量的增加，本文模型逐渐接近ZMC模型和KE模型，最终在完全塑性阶段相互重合。其中，CEB模型和KE模型的曲线都发生了跳跃的现象，这是由于CEB模型忽略了微凸体的弹塑性变形阶段，平均接触压力从弹性阶段的2/3kH增大到塑性阶段的kH；KE模型在曲线拟合过程中忽略了两个屈服临界点处曲线的平滑性。此外，本文模型和ZMC模型均采用样板函数，所以曲线是连续光滑变化的。值得注意的是，上述模型的微凸体接触半径均随着接触变形而变化的，但本文基于二次函数回转体的微凸体建模实现了对微凸体整体轮廓的拟合，能够在载荷较大的情况下，更加精确地进行结合面接触特性分析。

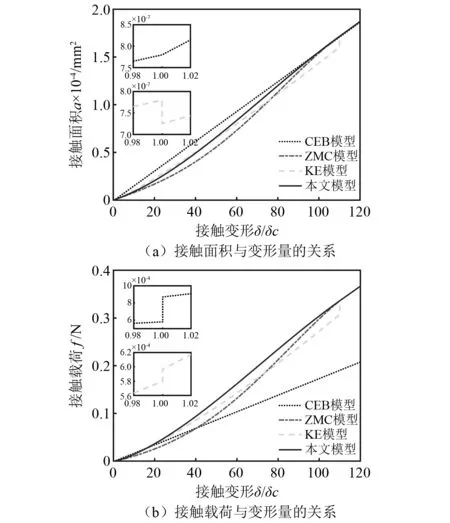
图6 不同微凸体接触模型对比Fig.6 Comparison of different asperity contact models

3.2 粗糙表面接触模型对比验证

图7为不同粗糙表面接触模型的无量纲接触面积A*、无量纲接触载荷F*分别与无量纲平均距离d*的关系。图7(a)和图7(b)显示，所有模型预测的接触曲线均随着平均距离的增大而逐渐减小为零。在平均距离较大时，粗糙表面的微凸体大部分处于弹性变形阶段，四种模型的差距很小。当平均距离为零时，四种模型的差距最大。从小到大来看，接触面积依次为0.064，0.068，0.075和0.111，接触载荷依次为6.42×10-4，8.05×10-4，8.39×10-4和1.13×10-3。本文模型的接触曲线均与ZMC模型和KE模型较为接近，而CEB模型的曲线明显偏大。这一现象的原因是本文模型、ZMC模型和KE模型都考虑了微凸体弹塑性阶段，但与其他模型的差异在于本文模型采用二次函数回转体模拟微凸体轮廓，建立了更加直观的微凸体接触半径与接触变形的解析关系。结合3.1节和3.2节的对比验证，可进一步说明了本文模型的有效性。

图7 不同粗糙表面接触模型对比Fig.7 Comparison of different rough surface contact models

4 讨论与分析

4.1 塑性指数对接触面积的影响

根据表1的表面参数，绘制无量纲接触面积A*与无量纲接触载荷F*的关系，如图8所示。不同塑性指数对应的表面参数分别为Ψ1=0.7，β1=0.033 9；Ψ2=1.5，β2=0.046 7；Ψ1=2.5，β1=0.060 1。

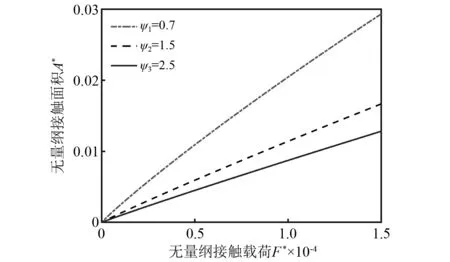
图8 不同塑性指数下接触面积与接触载荷的关系Fig.8 Relationship between contact area and contact load under different plasticity indices

由图8可知：①随着接触载荷的增大，不同塑性指数对应的接触面积也随之增大，呈现出近线性的关系，这是因为载荷增大，两表面的接触间隙减小，更多的微凸体受到挤压开始接触，增大了接触面积；②接触载荷越大，塑性指数对接触面积的影响越大；同等载荷条件下，塑性指数越大，接触面积越小。这是由于当塑性指数较大时，对应的表面粗糙度越大，虽然会有更多的接触微凸体进入塑性屈服状态，但单位面积上发生接触的微凸体数目较少，其接触面积也就越小。

4.2 塑性指数对接触刚度的影响

图9为无量纲接触刚度K*与无量纲接触载荷F*的关系。由图9可知：①不同塑性指数对应的接触刚度均随着接触载荷的增加而增大，相同载荷条件下，塑性指数越大，接触刚度越小，这是由于塑性指数越大，将会有更多的接触微凸体进入塑性屈服状态，表面抵抗弹性变形能力变弱，导致接触刚度降低；②接触载荷越大，塑性指数对接触刚度的影响越大。在接触载荷F*=1×10-4时，三种塑性指数对应的接触刚度分别为3.09，0.48，0.11，两两之间的差值分别为2.61，0.37。这说明，接触载荷较大时，不同塑性指数的接触刚度差异较大，塑性指数是影响接触刚度的主要因素。

图9 不同塑性指数下接触刚度与接触载荷的关系Fig.9 Relationship between contact stiffness and contact load under different plasticity indices

4.3 微凸体尺寸参数对接触刚度的影响

为研究微凸体尺寸参数对接触刚度的影响，选取图2中的粗糙表面(Ra2=1.302 μm)，测量位置如图1(b)所示的三条线段，获得三组微凸体尺寸参数：l1=15.273 μm,h1=1.039 μm；l2=16.790 μm,h2=1.082 μm;l3=17.985 μm,h3=1.065 μm。绘制不同微凸体尺寸参数的无量纲接触刚度K*与无量纲接触载荷F*的关系，如图10所示。由图10可知：①随着接触载荷的增加，接触间隙开始减小，相互接触的微凸体数目开始增多，接触面积变大，接触刚度亦随之增大；②同等载荷下，微凸体直径与高度的比值越大，接触刚度越大，这是由于微凸体直径与高度的比值越大，接触半径越大，从而产生更大的接触面积，粗糙表面抵抗弹性变形的能力就越强；③接触载荷越大，微凸体尺寸参数对接触刚度的影响较大。在接触载荷F*=1×10-4时，三种微凸体尺寸参数对应的接触刚度分别为0.25，0.21，0.18，两两之间的差值分别为0.04，0.03。与图10的刚度差值对比，进一步表明塑性指数对接触刚度的影响更大。

图10 不同微凸体尺寸参数下接触刚度与接触载荷的关系Fig.10 Relationship between contact stiffness and contact load under different asperity size parameters

5 结 论

(1) 提出一种采用二次函数回转体等效微凸体的建模方法，实现了对微凸体整体轮廓的拟合，建立了接触半径与接触变形的解析关系，弥补了半球体模型中单一曲率半径的缺陷。

(2) 根据二次函数模型，重新推导出微凸体在弹性、弹塑性和完全塑性的接触表达式，并应用接触力学理论和概率统计方法，建立了粗糙表面的微观接触模型。

(3) 对比分析了CEB模型、ZMC模型和KE模型与本文模型的差异。研究发现，本文模型的预测值与ZMC模型和KE模型较为接近，而CEB模型明显偏大；本文模型实现了对微凸体整体轮廓的拟合，更适用于重载情况下进行接触特性分析。

(4) 塑性指数是影响接触刚度的主要因素，塑性指数越大，其接触面积越小，抵抗变形的能力越弱；微凸体尺寸参数对接触刚度的影响较小，微凸体直径与高度的比值越大，接触面积和接触刚度越大。