基于模块化贝叶斯推理的随机非线性模型修正
王未寅, 王佐才,2, 辛 宇,3, 丁雅杰
(1. 合肥工业大学 土木与水利工程学院,合肥 230009; 2. 合肥工业大学 安全关键工业测控技术教育部工程研究中心,合肥 230009; 3. 合肥工业大学 安徽省基础设施安全检测与监测工程实验室,合肥 230009)
工程结构在遭遇台风、地震等极端荷载时,往往会呈现出较强的非线性特征,例如: 由材料特性引起的材料非线性、结构大变形引起的几何非线性以及结构边界非线性等,给工程结构的安全服役带来巨大的隐患。因此,研究结构在强荷载作用下的非线性行为,并对结构的非线性模型进行修正,不仅有助于对结构的安全状态进行准确评估,同时还可以预测结构在下一次强荷载作用下结构响应,为结构的安全预警及提前加固提供重要指导。
在结构进行非线性模型修正时,不可避免的会受到测量噪声、模型误差、有限元建模单元离散化等多种不确定性因素的影响,导致非线性模型修正的结果通常也具有不确定性。而传统的基于确定性的模型修正方法作为表征真实结构的一个特例,虽然可以根据一组试验数据准确地对非线性模型进行修正,但当预测结构在不同状态下的行为时,往往会产生较大误差。因此,结合统计学理论,考虑到不确定性因素对模型修正的影响,一些学者[1-8]提出了随机非线性模型修正方法,将非线性模型修正的结果以概率分布与置信区间的形式给出。其中,贝叶斯方法因其严谨的推理过程,在随机非线性模型修正中得到了广泛应用。例如, Xin等[9]利用非线性结构在地震荷载作用下的主分量瞬时幅值作为输入构建似然函数,结合最大似然估计和Cramér-Rao边界理论实现对非线性结构模型参数的修正,并量化由于测量误差引起的修正结果的不确定性。万华平等[10]采用贝叶斯方法实现随机模型修正,并将高斯过程模型与基于延缓拒绝自适应的随机采样(delayed-rejection adaptive metropolis-hastings,DRAM)算法相结合用于加快求解待修正参数的后验概率密度函数,并量化了由于测量误差引起的修正结果不确定性。刘纲等[11-12]在标准MCMC方法的基础上,引入了差分进化算法,通过多条马尔可夫链之间的随机差分运算来自适应选择条件分布以快速逼近目标分布,大大提高了采样效率,并对由测量噪声引起的修正结果不确定性进行量化。
测量误差和模型误差是引起模型修正结果不确定性的两个主要因素,然而,在基于贝叶斯推理的非线性模型修正研究中,测量误差通常被假设为是引起模型修正结果不确定性的主要原因。为了考虑模型误差对非线性模型修正结果的影响,部分学者对模型误差条件下,随机非线性模型修正结果的有效性进行研究。例如,Song等[13]利用非线性模态参数作为输入构建贝叶斯推理方法的似然函数,利用随机抽样算法对一根单梁试验结构非线性边界参数的后验概率分布样本进行估计,并初步探讨了模型误差对非线性模型修正结果的影响。
然而,上述研究均是对单一误差来源引起的不确定性进行分析,但当测量误差和模型误差同时存在时,如何开展随机非线性模型修正问题,是本文要研究的重要内容。因此,为了综合考虑多种不确定性因素对非线性模型修正结果的影响,本文提出一种基于模块化贝叶斯推理的随机非线性模型修正方法,该方法利用模块化的思想,将非线性结构的随机模型修正分为3个相互独立的模块。首先建立能够准确表征非线性结构模型动力响应的高斯过程替代模型作为模块一;其次为了尽可能准确的建立模型误差的高斯过程模型,先假设结构仅存在测量误差,通过过渡马尔可夫链蒙特卡罗(transitional Markov Chain Monte Carlo, TMCMC)[14]随机采样方法获得非线性模型待修正参数的后验概率分布样本,并将获得的后验样本均值看作非线性模型待修正参数的真实值,进一步构建非线性模型与实测结构关于动力响应瞬时加速度幅值的误差函数;然后,将引起模型误差的设计变量作为输入,误差函数作为输出,建立包含模型误差的高斯过程模型作为模块二;最后,结合模块一与模块二,利用TMCMC随机采样方法,将获得非线性模型待修正参数最终后验样本的过程看作模块三。为了验证该方法的可行性和有效性,本文对地震激励作用下的三跨连续梁桥进行数值研究,并对不同噪声水平、不同程度模型误差条件下的非线性模型修正结果进行研究。
1 随机非线性模型修正理论分析
1.1 非线性结构随机模型误差函数
对于非线性模型,假设模型在外部激励作用下的输出表示为
ym=ym(x,θ)
(1)
式中:x=[x1,x2,…,xd]为模型的设计变量,d为设计变量个数,x通常指在试验过程中根据先验信息设置的变量,或称为系统变量[15],例如,外部荷载激励、初始条件或模型的边界条件等;θ=[θ1,θ2,…,θr]为非线性模型的待修正参数,r为待修正参数个数,θ通常为试验时未知或者无法直接观测的非线性结构模型参数;ym为非线性模型响应的模拟结果。由于在非线性建模过程中,不可避免的存在模型简化或假设等问题,因此,即使获得了非线性模型的最优参数,但模型的预测结果与结构真实响应之间仍存在差异。这种误差可以用δ(x)表示,即为模型误差。因此,结构实测响应与非线性模型预测结果之间可通过式(2)表示
ye(x)=ym(x,θ*)+δ(x)+ε
(2)
式中:ye(x)为结构的实测响应;ym(x,θ)为有限元模拟结果,它是由设计变量x与模型参数θ共同决定的,θ*为待修正参数真实值;模型误差δ(x)则仅由设计变量x决定;ε为测量误差,通常假设为服从均值为零的高斯分布,即ε~N(0,Σexp),其中Σexp为试验观测值的误差协方差矩阵。等式(2)被称为模型修正方程[16],是进行非线性结构随机模型修正的基础,后续章节将进一步结合贝叶斯推理方法,对模型误差和测量误差同时存在条件下的非线性模型进行修正。
1.2 基于模块化贝叶斯推理的随机非线性模型修正
基于贝叶斯推理的随机非线性模型修正采用正向计算模型的方式解决了梯度计算困难、病态、非唯一解等诸多复杂逆不确定性量化难题。与传统的经典统计学相比,由于它同时结合了待修正参数的先验信息与实测信息,因此它给出更具可信度的参数后验概率密度函数,在随机非线性模型修正中被广泛使用。其理论公式为
(3)
式中:p(ye|θ)为给定参数θ时,结构实测响应ye发生的条件概率密度函数,也称作似然函数;p(θ)为待修正参数θ的先验分布,它反映待修正参数的先验信息,本文采用无信息先验分布的贝叶斯假设作为先验分布;c为一个与待修正参数无关的常数,起正则化作用;p(θ|ye)为待修参数的后验概率密度函数。
基于模块化贝叶斯推理的随机非线性模型修正方法则是在贝叶斯推理的基础上将整个模型修正过程分成非线性结构系统高斯过程替代模型、模型误差高斯过程模型与待修正参数后验采样计算3个相互独立的模块。在进行采样计算时,结合模型误差高斯过程模型与测量误差构建似然函数,解决了传统随机非线性模型修正中模型误差与测量误差难以同时考虑的问题,基于模块化贝叶斯推理的随机非线性模型修正方法具体的操作流程,如图1所示。

图1 基于模块化贝叶斯推理的随机非线性模型修正流程图Fig.1 Stochastic nonlinear model updating flow chart based on Modular Bayesian inference
1.2.1 非线性结构系统的高斯过程模型(模块一)
高斯过程模型是基于贝叶斯理论构建的,它采用高斯先验定义模型输出,通过对训练样本的最大似然估计得到预测样本的后验高斯分布。它除了具有计算效率快、拟合精度高等诸多优点外,还可以对预测值的不确定性进行估计,因此被广泛应用于高维、强非线性等复杂有限元结构的替代模型选择。为了提高后续采样计算效率,全面考虑模型修正过程中的多种不确定性因素影响,本文采用高斯过程模型构建非线性结构系统的替代模型,其具体建立方法如下所示:
首先,根据计算机试验设计方法,生成关于设计变量x与待修正参数θ的训练样本点,并计算非线性模型在相应训练样本点下的结构动力响应瞬时加速度幅值:然后,将设计变量x与待修正参数θ作为输入,将相应的结构动力响应瞬时加速度幅值作为输出,构建非线性模型的高斯过程替代模型,并验证替代模型的拟合精度。将非线性系统结构的高斯过程模型看作模块一。
1.2.2 模型误差的高斯过程模型(模块二)
模型误差δ(x)是导致非线性模型修正结果不确定性的重要原因之一,但由于模型误差无法直接观测,通常又与其他误差混淆。因此,如何量化模型误差对修正结果的影响是随机非线性模型修正研究的一项重要内容。在传统的随机非线性模型修正中,通常不考虑模型误差的影响,或将模型误差直接放在参数的不确定性中。但当模型跟真实结构之间存在较大模型误差时,一方面可能会导致修正后的模型参数失去物理意义,同时,当较大的模型误差存在时,即使修正后的模型能够对当前状态下的结构响应进行准确预测,但不能准确地预测结构在下一次激励作用下的动力响应,从而导致非线性模型修正的结果失去应用价值。
由于模型误差是非线性结构真实响应与计算模型在待修正参数真实值条件下输出响应之间的差值,因此只有首先确定待修正参数的“真实值”θ*才能准确构建模型误差的高斯过程模型,但在实际试验时,结构待修正参数的真实值θ*往往未知。目前常见的解决方法是直接将待修正参数的先验均值θprior当作待修正参数的真实值θ*,并分别将设计变量x作为输入,将ye(x)-ym(x,θprior)作为输出构建模型误差的高斯过程模型[17-18]。但当工程师根据经验设置的非线性参数先验均值与参数真实值相差较大时,模型误差的高斯过程模型建模则失去意义。为了尽可能准确的建立模型误差的高斯过程模型[19],本文采用如下建模方法:
首先假设非线性模型与真实结构之间仅存在测量误差,则等式(2)可以简化成
ye(x)=ym(x,θ*)+ε
(4)
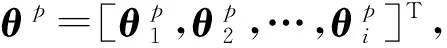
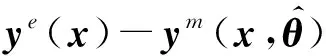
1.2.3 待修正参数后验概率密度函数求解(模块三)
由模块一与模块二高斯过程模型可知ym(x,θ)与δ(x)均服从高斯分布,测量噪声通常假设为服从零均值的高斯分布,结合式(2)可知ye(x)将服从均值为ym+δ,方差为Σ的多维高斯分布,待修正参数θ的后验概率密度函数可表示为
(5)
式中:Σ为似然函数的协方差矩阵,其中包含多种不确定性误差作用;Σexp为由测量噪声等引起的测量误差协方差矩阵;Σbias为模型误差高斯过程模型的协方差矩阵;Σcode为替代模型拟合精度的误差协方差矩阵;Σcode与Σbias分别由模块一和模块二的高斯过程替代模型得到。
由于采用贝叶斯方法的待修正参数后验概率密度形式较为复杂,且当参数维度较高时,其解析解难以通过积分求解。因此,通常利用马尔可夫链蒙特卡罗采样方法获得非线性模型待修正参数θ的后验概率分布函数。但传统的标准MH采样算法在采取高维参数时,容易出现采样“停滞”的现象,待修参数收敛较慢,甚至无法收敛。而TMCMC随机采样方法通过在参数先验分布与后验分布之间加入一系列“中间分布”,解决了直接根据后验概率分布采样困难的问题。
TMCMC算法虽然通过加入一系列中间分布解决了直接根据后验采样困难的问题,但仍存在计算量大的缺点,每组待修正参数后验样本的迭代均需调用有限元模型进行结构动力分析,当参数维度较高时,待修正参数先验与后验之间往往会过渡多个中间分布,而每一个中间分布均需要采取相应数量的样本,因而计算任务十分巨大。为了实现后验概率密度函数的快速计算,模块三结合了模块一和模块二的高斯过程模型,利用数值模型替代有限元模型进行非线性结构动力响应预测,从而大幅提高后验样本的计算效率。
2 数值验证
2.1 三跨连续梁桥非线性模型建立
为了验证本文所提非线性结构随机模型修正方法的可行性和有效性,利用Opensees有限元分析软件对地震激作用下的三跨连续梁桥进行数值研究,建立的桥梁结构模型如图2所示,桥梁总体跨径布置为3×30 m,桥墩高度为10 m。主梁结构采用线弹性梁柱单元进行模拟,桥墩采用基于纤维截面的非线性梁柱单元定义。桥墩的混凝土材料采用Concrete 02进行定义,钢筋采用Steel 02材料进行模拟,两类材料的本构模型分别如图3和图4所示,通过设置不同的非线性材料参数实现对结构非线性特征的模拟。其中,为了模拟主梁支座在地震作用下的边界非线性效应,主梁支座采用具有剪切非线性特征的支座单元进行模拟,支座单元的弹塑性特征如图5所示。图5中:k0为非线性支座的剪切刚度;α1与α2分别为支座单元线性与非线性硬化组件的屈服刚度比;μ为非线性硬化指标。
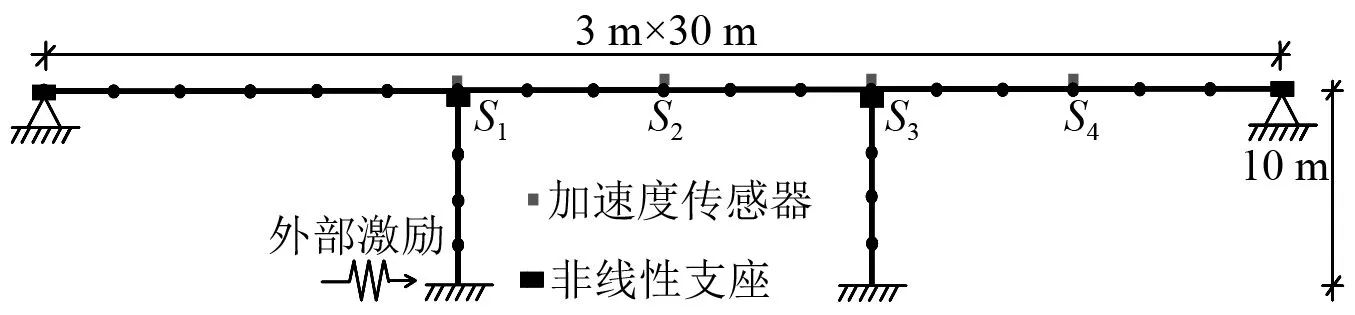
图2 三跨连续梁桥非线性模型Fig.2 Nonlinear model of three-span continuous beam bridge
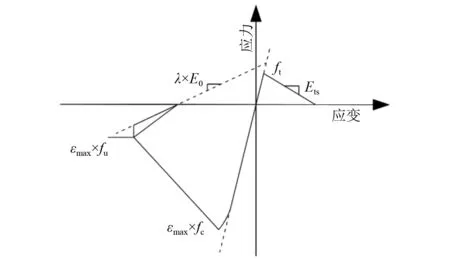
图3 Concrete 02 材料Fig.3 Concrete 02 material
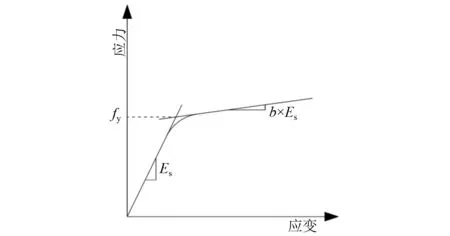
图4 Steel 02材料Fig.4 Steel 02 material
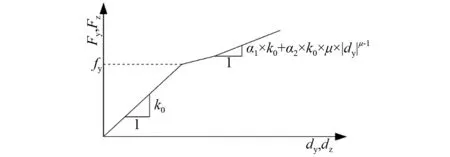
图5 非线性支座单元Fig.5 Nonlinear bearing element
针对该桥梁结构的非线性参数,如非线性材料本构参数、非线性边界参数等,首先利用灵敏度分析方法[20],选取对结构动力响应较为灵敏的7个非线性参数作为待修正参数。选取的非线性模型待修正参数主要包括:钢筋的屈服强度fy、初始弹性模量Es和应变硬化比b;混凝土的抗压强度fc、峰值压应变εmax;非线性支座的剪切刚度k0以及特征强度Qd,非线性待修正参数的理论值如表1所示。考虑到边界条件相对于材料参数具有更高的不确定性,因此,本研究将支座单元的非线性硬化指标μ作为模型的设计变量,用来定义桥梁结构的模型误差。本文取μ理论值为2。然而,对于复杂的土木工程结构,引起模型误差的因素有很多,如模型简化、节点等效、非线性材料本构假设等,往往需要选择更多的设计变量表征模型误差。考虑到本文的主要目的是为了验证方法的可行性和有效性,因此,本算例仅选取支座单元的非线性参数μ作为模型误差来源;在进行桥梁结构的非线性动力响应计算时,选择的外部激励为1940年的El Centro地震波,持续时间为30 s,采样频率为50 Hz,地震激励如图6所示。利用Newmark-β积分算法对结构在地震荷载激励作用下的加速度响应进行计算,加速度传感器S1~S4布置图见图2。

图6 地震荷载Fig.6 The seismic loads

表1 非线性待修正参数理论值Tab.1 Theoretical values of the candidate nonlinear parameters
2.2 基于模块化贝叶斯推理的桥梁结构随机非线性模型修正
在进行桥梁结构的随机非线性模型修正时,将2.1节中所述的7个非线性参数作为非线性模型的待修正参数。其中为了同时考虑模型不确定性与测量不确定性对修正结果的影响。本文先使用Sobol序列采样方法在设计变量μ理论值上下10%范围内产生100组试验输入样本,计算结构在相应设计变量与非线性参数名义值组合下的结构动力响应。另外在响应中添加5%的随机高斯白噪声,模拟实测动力响应数据。然后,利用离散解析模态分解和希尔伯特变换对结构的动力响应进行分解,提取动力响应主分量的瞬时加速度幅值,并从其中选取300个局部峰值点作为非线性指标。其中,传感器S2记录的加速度响应的瞬时幅值识别结果,如图 7所示。基于模块化贝叶斯推理的三跨连续梁桥的随机非线性模型修正过程如下:

图7 中跨跨中动力响应主分量瞬时加速度幅值Fig.7 Instantaneous amplitude of the acceleration response in mid-span
2.2.1 构建地震荷载作用下,三跨连续梁桥的高斯过程替代模型(模块一)
训练数据样本点的选取对高斯过程模型的构建至关重要,经典的试验设计方法(design of experiment,DOE)譬如均匀设计法、中心复合设计法等被广泛用于多项式响应面模型的构建。但这些经典的试验设计方法受限于试验成本与环境等因素有一个共同的特点,即试验点位于参数空间的边缘和中心,无法覆盖整个参数空间。而本文所涉及的试验为计算机试验,即通过计算机模拟物理系统输入输出关系的试验,不受试验环境和条件等因素的限制。作为常用空间充满采样方法之一,Sobol序列在所有维度上均以素数2为基,使得样本不仅在高维上具有较高的均匀性,而且便于利用点位运算,大大提高了计算机计算效率[21]。因此,本文选用Sobol序列采样方法进行试验设计。
通过Sobol序列采样方法在参数理论值上下20%范围内生成1 000组参数样本,其中参数包含上述一个设计变量μ及7个待修正参数θ,利用Opensees有限元模型计算结构相应的动力响应瞬时加速度幅值。分别将设计变量μ与非线性待修正参数θ作为输入,将相应目标响应瞬时加速度幅值作为输出,构建Opensees非线性模型的高斯过程替代模型。使用留一交叉验证方法验证替代模型的预测精度,以第2 s处中跨跨中的结构动力响应瞬时加速度幅值为例,其交叉验证残差的正态分位图如图8所示。由图8可知,交叉验证残差的正态分位图趋向于一条直线,残差的正态特性较好,所建立的高斯过程模型可以准确地预测结构动力响应瞬时加速度幅值。

图8 模块一残差正态分位图Fig.8 Normal quantile-quantile of module 1
2.2.2 构建非线性三跨连续梁桥模型误差的高斯过程模型 (模块二)
模块二中模型误差的高斯过程模型建立方法如1.2.2节所示。即先假设模型不存在模型误差,利用TMCMC随机采样方法获得非线性待修正参数θ的后

图9 模块二残差正态分位图Fig.9 Normal quantile-quantile of module 2
2.2.3 待修正非线性结构模型参数后验概率密度函数计算(模块三)
模块一与模块二建立后,再结合两模块,根据模型修正方程与式(5)在模块三中通过TMCMC随机采样方法,采取待修正参数θ的1 000组后验分布样本,其样本直方图如图10所示。由图10可知,非线性待修正参数的TMCMC随机抽样样本基本符合正态分布样本特征,可以根据中心极限定理估计出待修正参数的均值与方差等数字特征。
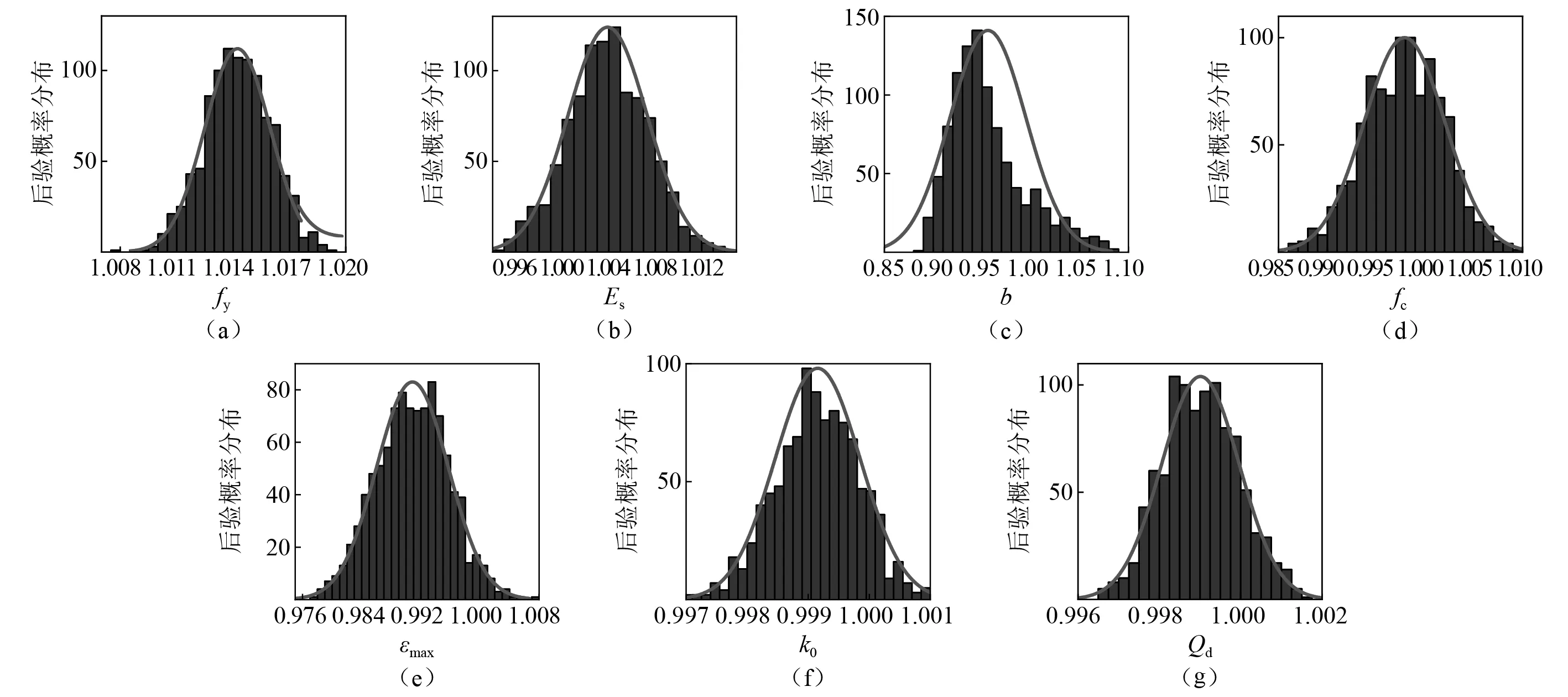
图10 非线性参数TMCMC采样样本分布直方图Fig.10 Histogram of sample distribution of TMCMC samples for the nonlinear parameters
在数值模拟过程中,采用的计算机CPU为Intel(R) Core(TM) i5-8500(3.0 GHz),内存配置为8 GB,整个模型修正过程需要进行两次TMCMC采样,每次TMCMC采样至少包含16个过渡阶段,每阶段采样1 000次,完成整个模型修正共耗时约2.39 h。若不采用高斯过程替代模型,直接使用非线性有限元模型进行采样,进行一次采样所需时间约为26 s,完成整个模型修正过程预计耗时约231.11 h;此外,为了提高待修正参数的估计精度,本研究分别利用TMCMC算法与MH算法进行待修正参数的后验采样,计算结果如表2所示。为了能直观反映非线性参数的修正误差,对本文待修正参数均进行归一化处理。

表2 5%噪声水平下非线性模型修正结果Tab.2 The nonlinear model updating results under 5% noise level
由表2可知,利用TMCMC算法的非线性参数估计结果具有更高的精度,且参数误差均低于5%;然而,基于MH采样算法的最大估计误差为14.423%,远低于TMCMC的采样精度。因此结合高斯替代模型与TMCMC算法进行非线性模型修正,能够有效地增强计算效率,并提高修正精度。利用后验样本均值来估计非线性模型待修正参数,并代入Opensees进行计算,得到结构的加速度响应与真实响应对比,如图11和图12所示。修正后的节点加速度响应与真实值响应吻合较好。为了能直观的量化修正前后加速度响应的修正误差,使用二范数Er作为误差指标,其具体计算方法如式(6)所示

图11 S2测点加速度响应修正结果Fig.11 The updated results of the acceleration responses obtained from sensor S2
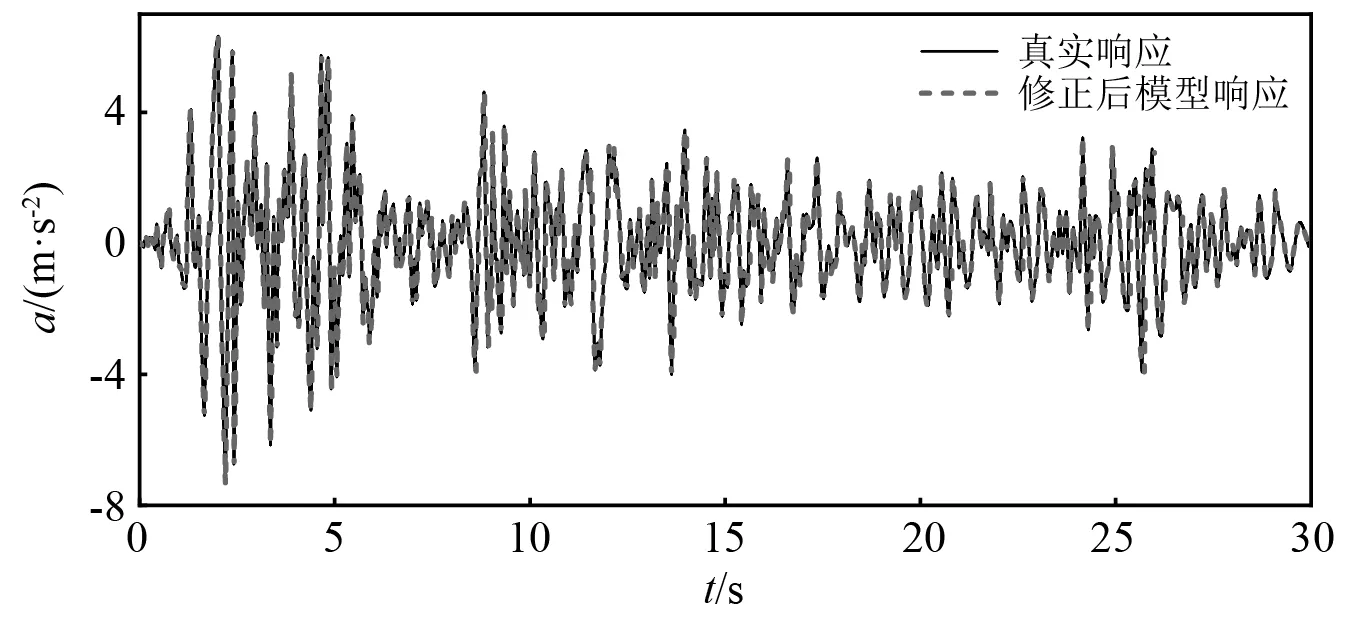
图12 S1测点加速度响应修正结果Fig.12 The updated results of the acceleration responses obtained from sensor S1
(6)
式中:yr为结构的真实响应;yp为修正后结构的预测响应。修正后的4个节点加速度响应误差,如表 3所示。

表3 计算的误差指标Tab.3 The calculated error indices 单位:%
由表3可知,修正后的结构动力响应与真实响应误差较小,其中最大误差也在1.6%以内,因此采用本文所提出的模块化贝叶斯方法可以在同时考虑测量误差与模型误差的基础上满足修正精度要求,可以应用于考虑多种不确定性因素的非线性模型修正问题。
3 非线性结构模型修正的鲁棒性研究
3.1 不同测量噪声水平下的非线性模型修正研究
为了研究本文所提非线性结构随机模型修正方法的抗噪性,本节分别对比了在5%,10%,20%三种不同噪声水平作用下的模型修正结果。其中在每一种噪声水平作用下,又分两种工况对比了初始参数不确定性对模型修正的影响。其中工况一中的待修正参数是一组确定值;工况二的待修正参数则是考虑结构初始参数的不确定性,服从均值为真实值θ*,标准差为0.05θ*的正态分布。其修正结果如表4~表6所示。
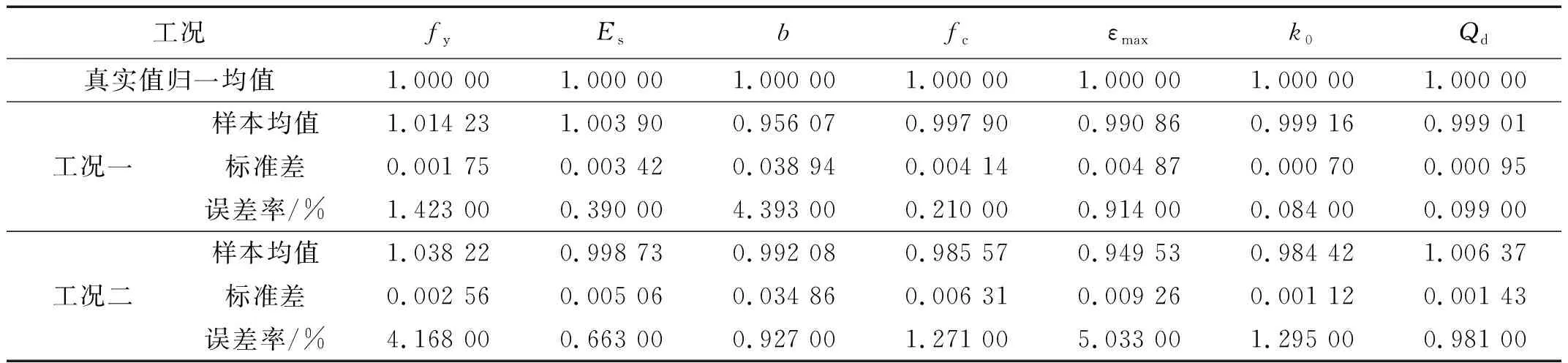
表4 5%噪声水平下不同工况修正结果对比Tab.4 Comparison of the updated results of the different cases under 5% noise level
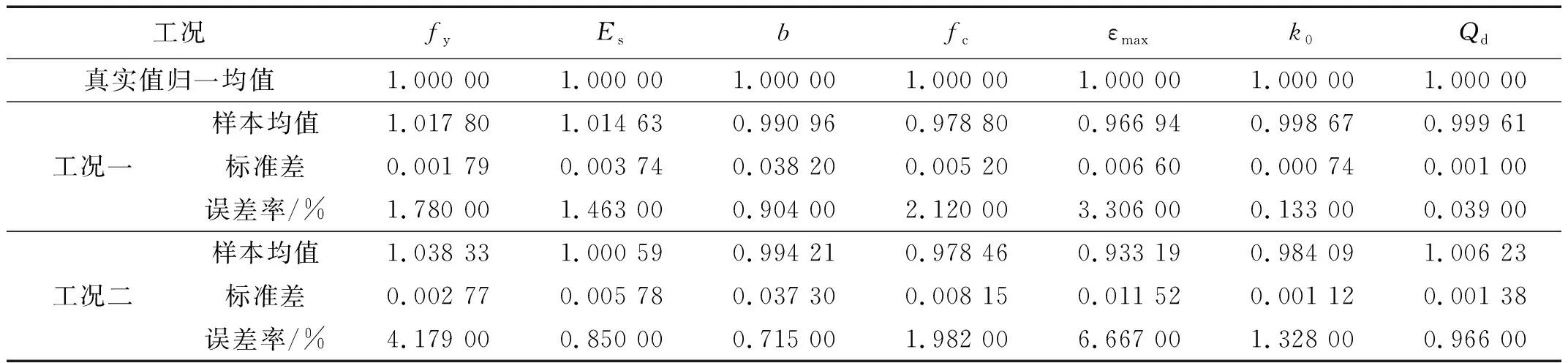
表5 10%噪声水平下不同工况修正结果对比Tab.5 Comparison of the updated results of the different cases under 10% noise level

表6 20%噪声水平下不同工况修正结果对比Tab.6 Comparison of the updated results of the different cases under 20% noise level
由表4~表6可知,在不同噪声水平作用下TMCMC采样样本均值均接近真实值均值。待修正参数修正误差较小,由此可知本文所提方法拥有较好的抗噪性能,在高噪声水平条件下依然可以准确修正模型。
对比表4~表6在同一噪声水平作用下,工况一与工况二的采样标准差可以发现,由于工况二相较于工况一多考虑了模型初始参数不确定性的影响,因此工况二的采样标准差要大于工况一;除此之外,在同一工况下,随着噪声水平的增加,样本的标准差也在逐渐增加。由上述结果可知采样样本的标准差随着结构不确定性因素的增加逐渐增加。
3.2 不同模型误差水平下的非线性模型修正研究
为了研究本文所提非线性结构随机模型修正方法的鲁棒性,探究设计变量的变化程度对模型修正结果的影响,本节分别对比了在使用Sobol序列采样方法进行试验设计时,设计变量μ在理论值上下5%范围产生试验输入,与10%范围产生试验输入两种不同情况下的模型修正结果,非线性模型修正结果如表7和表8所示。

表7 不同模型误差条件下工况一非线性模型修正结果Tab.7 The nonlinear model updating results of case 1 under different model uncertainties 单位:%
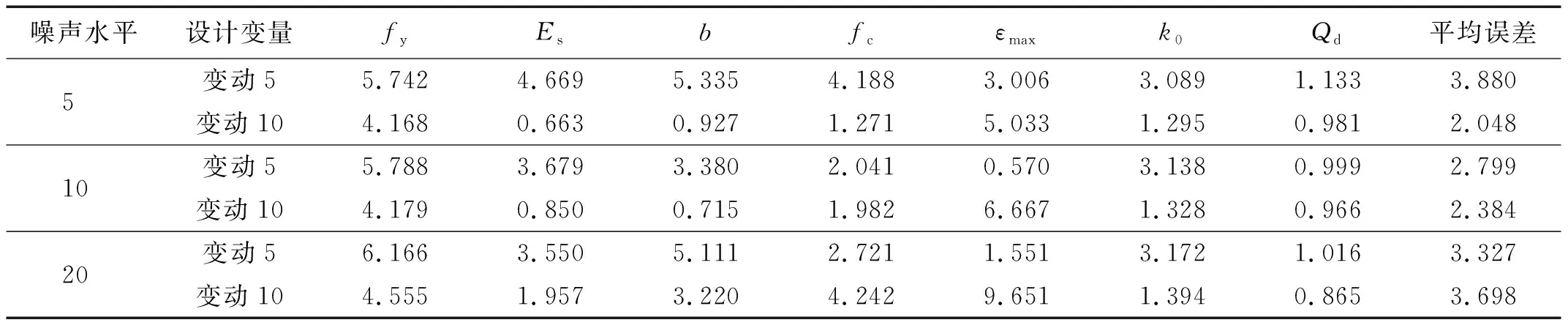
表8 不同模型误差条件下工况二非线性模型修正结果Tab.8 The nonlinear model updating results of case 2 under different model uncertainties 单位:%
表7和表8分别为工况一、工况二条件下,模型误差水平对非线性参数修正结果的影响。由表7和表8可知,设计变量无论在理论值5%范围内变动,还是在10%范围内变动,均能保证较高的修正精度。其中待修正参数的误差率随着噪声水平的逐渐增加与设计变量变动范围的增大有些许增大,但平均误差均在4%以内。因此使用本文所提出的方法,可以在结构设计变量变化较大情况下,仍能保证预测结果的准确与可靠性。
4 结 论
本文采用模块化贝叶斯的方法,将整个模型修正过程分成3个模块,基于实测结构动力响应主分量的瞬时加速度幅值,构建同时考虑测量误差与模型误差的似然函数,并结合高斯过程模型与TMCMC算法,实现了随机非线性模型修正及非线性待修正参数的不确定性量化。通过对地震激励作用下三跨连续梁桥的数值研究可以得出以下结论:
(1) 所提方法通过引入设计变量,将难以单独建模的模型误差巧妙表示出来,并结合模块化方法在贝叶斯理论框架下,实现了同时考虑模型误差与测量误差等多种不确定性因素作用下的随机非线性模型修正,并对参数的不确定性进行量化。
(2) 通过将高斯过程模型与TMCMC算法相结合,克服了传统MCMC算法高维采样收敛慢,计算效率低的缺点,大大提高了采样效率。
(3) 与不考虑初始参数不确定性相比,考虑模型初始参数不确定性的非线性参数修正误差与标准差更大,更能真实地反映结构的安全状态,因此在结构安全评估时,采用考虑模型初始参数不确定性的模型修正结果,能更好的反映实际结构的抗灾害能力。
(4) 本文仅对单一的模型误差展开了相关研究,然而,对于复杂的土木工程结构,引起模型误差的因素通常有很多,如模型简化、节点等效等。因此,如何对多种模型误差条件下的非线性模型进行修正需要进一步被研究。
(5) 本文为了对多重不确定因素下的非线性结构模型修正问题进行研究,将模型误差视为服从高斯分布,但该假设具有一定局限性。因此如何建立非高斯分布条件下的模型误差替代模型需要进一步被研究。

