基于模拟退火算法优化增益的车辆传动比算法设计
陈哲明,庄威洋,陶 军
(重庆理工大学 车辆学院,重庆 400054)
线控转向系统取消方向盘与转向轮之间的直接机械连接,由电子控制单元(Electronic Control Unit, ECU)控制电机转向[1]。由于机械转向系统方向盘与前轮转角比值为固定值,或仅可在小范围内变动,车辆的转向特性具有强非线性特征[2]。驾驶员需要调整操作适应车辆转向特性的变化,对驾驶产生额外的精神负担。
而线控转向(Steer By Wire, SBW)系统由控制器控制转向角,传动比可以自由设置,并不局限于固定值。通过变传动比设计,使车辆在全车速段具有期望转向特性。因为不存在机械结构的直接连接,转向系统力特性与角特性完全解耦,可以独立设计。根本上解决传统转向系统在低速段与高速段的性能的矛盾[3]。
关于线控转向系统,国内外已有一定的研究。卢少波等基于磁流变设计了路感反馈系统,并进行了相关的优化[4]。杨莉等提出一种基于位置-力矩混合方法的线控转向系统双向控制算法优化线控转向系统的控制效果[5]。公伟强基于全状态反馈控制策略,优化线控车辆的转向特性,提高车辆操纵稳定性[6]。JEFFREY C等依据路感电机线性关系,以路感电机电流为基础,研究线控转向系统的力传动特性[7]。AZZALINI M等针对“人车路”闭环系统模型强非线性特征,基于模糊算法,参考车速、转角、侧向加速度等多变量设计变传动比[8]。YAO等针对模糊算法过于依赖设计者经验,引入模糊神经网络调节模糊隶属函数及模糊规则设计变传动比[9]。周兵等通过对比分析多种传动比拟合曲线后,选择S函数对角传动比数据进行拟合,通过平滑处理的i曲线控制执行电机,使输出更加平滑[10]。赵林峰等改进滑膜控制,通过可拓滑膜控制,基于前路转角补偿,设计变传动比及转向轮转角控制器[11]。董铸荣等参照4WIS,进行了方向盘至后转向轮的传动比研究与设计[12]。
本文以定增益法为基础,通过车速、方向盘转角多变量共同设计线控转向车辆理想传动比。对定增益传动比。通过模拟退火算法(Simulated Annealing, SA)优化定横摆增益值,以郭孔辉院士提出的操纵稳定性综合评价指标作为目标函数,优化得到全局最优解。对比研究传统转向系统车辆和SBW车辆,分析所设计传动比算法对车辆转向性能的影响。
1 线控转向车辆模型建立
线控转向车辆与传统车辆主要区别在于转向系统不同。建立线控转向系统模型,替代机械转向系统得到整车模型。利用整车模型进行后续传动比算法的研究。
1.1 操纵稳定性二自由度车辆模型
车辆简化二自由度模型,可以反映车辆转向的最基本特征,包含车辆最主要的参数特征与轮胎侧偏参数。且二自由度模型研究成熟可靠,与线控转向车辆的变传动比研究十分适合。
参照车辆坐标系,通过将车辆简化为二轮模型,对二轮车辆进行分析。
图1为车辆的运动与受力分析。
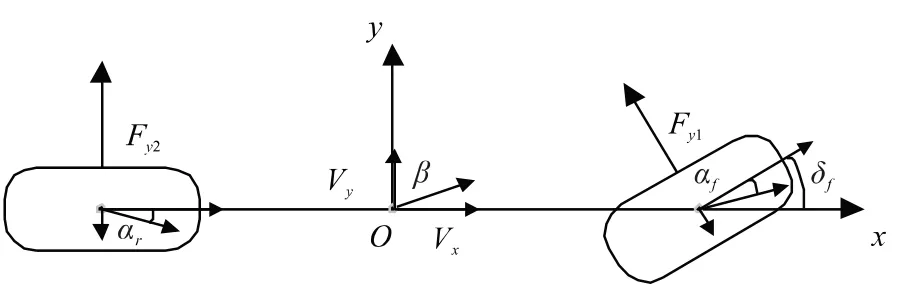
图1 操纵稳定性二自由度模型图
其中,Fy1、Fy2分别为前后轮所受侧向力;αf、αr分别为前后轮侧偏角;δf为等效转向轮转角输入;β为质心侧偏角;Vx、Vy分别为纵向速度与侧向速度。
经分析与化简,二自由度模型最终动力学方程式可表示为

由二自由度模型前轮稳态横摆角速度增益为

二自由度模型可分析前轮至车辆的响应,由SBW转向系统模型可分析方向盘至前轮响应。结合SBW系统模型与二自由度模型,可研究由方向盘至车辆的响应。
1.2 线控转向系统动力学模型
SBW系统主要分为路感模拟总成及转向执行总成。本文主要以 SBW 系统角传动比为研究对象,主要针对转向执行总成进行研究。
图2为转向执行总成结构图。

图2 转向执行总成结构图
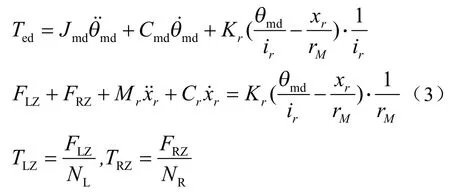
式中,Ted为电机转矩;Jmd为电机等效惯量;Cmd是电机等效阻尼;Kr为小齿轮轴刚度;θmd为电机转角;xr为齿条位移;rM为小齿轮半径;ir为电机减速比;F为齿条力;Mr为齿条质量;Cr为转向器等效阻尼;T为回正力矩。
线控转向系统采用直流有刷永磁电机,建立动力学方程:

式中,Um为执行电机电压;Rm为电阻;Lm为电感;i为电流;Km为反电动势系数;θm为电机转角;Ted为输出转矩;Kt为电机转矩系数。
1.3 整车仿真模型
建立SBW系统模型,替换传统车辆的机械转向系统模型,并在Simulink中建立控制器模块,控制转向轮转向。
通过上文分析所得动力学方程,利用Simulink搭建整车模型。
2 变传动比算法设计原理
由于线控转向系统取消了方向盘与转向轮之间直接的机械连接,采用控制器控制转向执行电机驱动转向轮转向。因此,转向轮与方向盘之间传动关系由算法决定,并未受到机械结构的限制,可以自由设计。
角传动比的设计为线控转向系统的重要研究方向。
变传动比设计主要包含 3种方法:(1)智能算法设变传动比;(2)基于定增益设计法;(3)综合多增益比例设计法。三种方法各有优劣,本文不做详细研究。
本文采用基于定横摆角速度增益法进行设计[13]。
2.1 定稳态横摆角速度增益变传动比
根据定增益法设计,期望方向盘转角dsw到车辆稳态横摆角速度响应wr为定值。记为

传动比定义为

式中,dsw为方向盘转角;df为等效前轮转角。
据稳态前轮横摆角速度增益,即前轮转角至车辆稳态横摆角速度响应:

因此,可得传动比的计算表达式:

根据式(8),由前轮稳态横摆角速度增益Gf与方向盘稳态横摆角速度增益GSW可计算出对应的传动比值。
2.1.1 前轮横摆角速度增益
根据式(7),在u=30,40,…,110,120 km/h共10种车速工况下进行测试。将零转角输入到极限转角输入10等分,在每一车速工况下测试10种不同角阶跃输入响应。
据每次一工况下所得的稳态横摆角速度wr以及等效前轮转角数值df,由定义式可得对应车速与前轮转角下的前轮横摆增益值Gf。
图3为其中一种工况下的测试结果,车速u=120 km/h,前轮转角阶跃输入df=1.2°。

图3 角阶跃输入测试
对所有工况进行测试,结果不完全列出。根据结果计算得到前轮横摆角速度增益。
限制车速范围为0 km/h~140 km/h,方向盘转角为0 deg~180 deg,采用最小二乘插值法,对测试所得离散前轮增益值进行插值,得到在全车速和转角范围内的Gf值。
根据式(8)传动比计算式,暂时依据经验,选取定方向盘转角增益Gsw=0.5,计算得到全车速及方向盘转角下的传动比算法。如图4所示。

图4 基于定Gsw的变传动比算法
2.2 变传动比算法改进
由定增益法所确定的理论传动比算法,当传动比极小之时,驾驶员输入很小的方向盘转角就会产生极大的横摆角速度,车辆会发生激转,失去稳定,这是必须避免的情况。并且转向系统的物理结构存在限制,无法响应过大输入。因此,对于传动比算法取最值限制。
并且设计传动比时,期望车辆可以拥有在低速时灵敏,高速时稳重。小方向盘转角输入时灵敏,转角过大时稳重的特性。因此,对传动比算法取单调限制。
因此,对传动比算法做出以下优化:
(1)限制imin=6,imax=22;
(2)改进传动比使随u增大,i单调增大或不变。
根据以上原则进行改进,得到改进后传动比算法,如图5所示。

图5 改进变传动比算法图
3 基于模拟退火算法定增益值优化
本文采用模拟退火算法对定增益值Gsw进行优化,确定全局最优增益值,以此作为变传动比算法设计依据。
3.1 模拟退火算法
SA算法是基于金属退火物理过程提出的一种通用算法,属于 Monte-Carlo 迭代求解策略的一种随机寻优算法,其流程如图6所示。
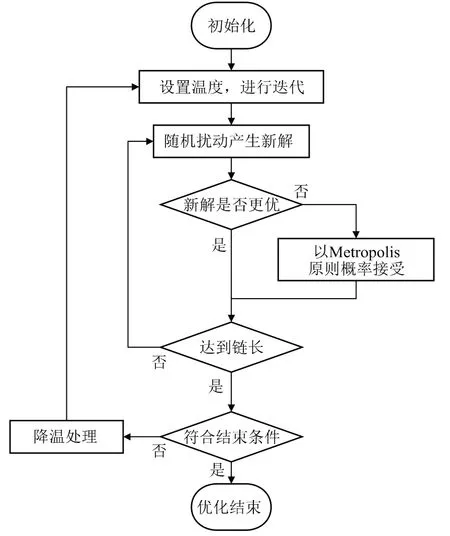
图6 SA算法流程图
SA算法从较高初始温度T0开始,由初始解x0计算相应目标函数值,并在x0领域内随机扰动产生新解xt+1,计算对应目标函数,求取最优解或依照 Metropolis原则以一定概率接受恶化解,以跳出局部最优,随机寻求全局最优解。
Metropolis原则如下:

在当前温度迭代后依据Tt+1=kTt降低温度继续进行优化。随着温度的降低,接受恶化解的概率降低,产生扰动范围变小,新解xt+1据xt较近。最终在低温冷却后趋于全局最优解[14]。
3.2 操纵稳定性综合评价指标
应用 SA算法进行优化定增益值的关键是确定目标函数。
郭孔辉院士所提出的操纵稳定性综合评价指标(记为FH)。其中包括:路径跟踪指标、操纵负担指标、侧翻指标、侧滑指标。包含了车辆最重要的转向特性,可以有效地分析车辆转向性能,因此,选用综合指标值作为SA算法优化函数值[15]。
1.路径跟踪指标
(1)路径跟踪误差:

式中,f(t)为驾驶员期望路径;y(t)为汽车实际行驶路径;为轨迹误差标准门槛值;tn为试验时间。
(2)方向误差:

式中,Vx为纵向速度;为质心侧偏角速度;为质心侧偏角加速度标准门槛值。
(3)取以上加权均值后得到总路径跟踪指标:

式中,We1和We2为权值。
2.操纵负担指标
(1)驾驶员忙碌程度:

(2)沉重程度:

式中,Tsw为方向盘转矩;为方向盘转矩标准门槛值。
(3)取以上加权均值后得到总驾驶员操纵负担指标:

式中,Wb1和Wb2为权值。
3.侧翻指标
(1)侧向加速度指标:

式中,ay为侧向加速度;为侧向加速度标准门槛值。
(2)侧倾角指标:

式中,φ为侧倾角;为侧倾角标准门槛值。
(3)取以上加权均值后得到侧倾指标为

式中,Wr1和Wr2为权值。
4.侧滑指标

式中,Fyi为某轴受到的侧向力;Fzi(t)为某轴的轴荷;Jsi为此轴侧滑危险性指标;Js为整车侧滑危险性指标;为侧向附着系数的标准门槛值。
3.3 横摆角速度增益优化及最终传动比i确定
根据经验选取增益值Gsw=0.5为初始值,得到相应传动比算法。利用Simulink进行仿真测试,将车辆运行参数导入Matlab进行计算,得到相应工况下的综合指标值FH。
以增益值Gsw为变量,综合指标值FH值作为目标函数值,将以上求解代码模块化,作为SA算法目标函数。
关于 SA算法关键参数,选取增益初始值Gsw=0.5,优化区间[0.01,1],迭代次数L=100,降温系数k=0.95。
选取双移线工况,在u=30,45,60,…,120 km/h共7个车速工况下进行测试。利用SA算法进行优化,得到在各自车速下最优的定增益值。
不同车速工况下对应最优横摆增益值Gsw值如表1所示。

表1 不同车速工况最优Gsw值表
基于不同Gsw值设计 7种对应传动比算法。对每种传动比算法在各车速段下进行测试,计算操稳综合指标值,对各车速工况下FH值取加权进行分析。结果表明定增益值Gsw=0.341时,对应传动比算法测试结果加权指标值最小,且在全车速段内都具有良好操纵特性。
最终选取Gsw=0.341作为最终采用定增益值。依照前文步骤,基于Gsw=0.341设计传动比,并进行改进,确定最终传动比。如图7所示。
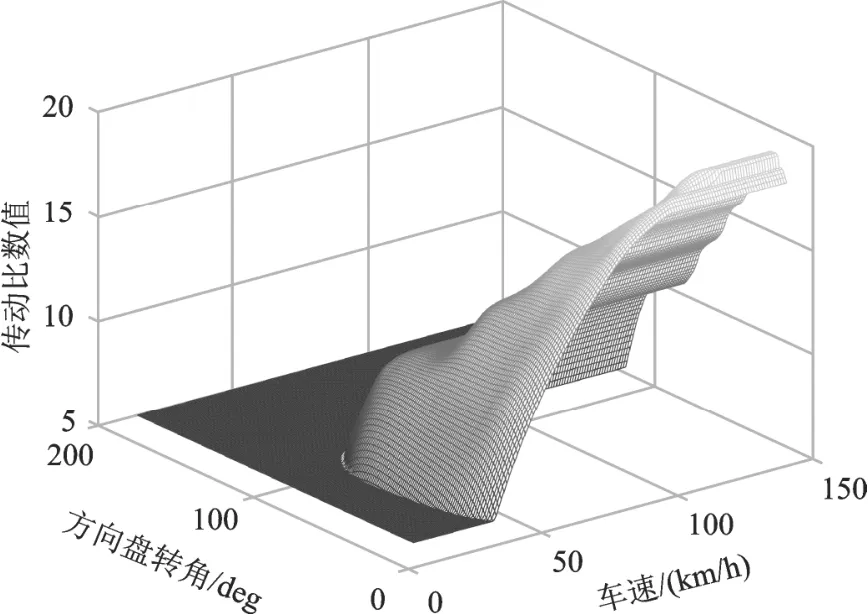
图7 最终传动比算法
4 SBW车辆仿真分析
根据传动比算法,利用 Smulink搭建传动比模块,嵌入整车模型进行仿真测试。对比分析基于优化前后增益值所设计的传动比算法对 SBW系统车辆转向性能影响。
4.1 双移线试验工况
设置车速u=80 km/h,良好路面,无外界干扰,进行双移线工况试验。基于优化前后增益值所设计的传动比算法进行测试。结果如图8—图10所示。
由图 8对比分析可知,增益值优化后传动比算法对期望路径跟踪效果更好,转弯后回到直线路径的速度也更快,整体转向效果比优化前更好。
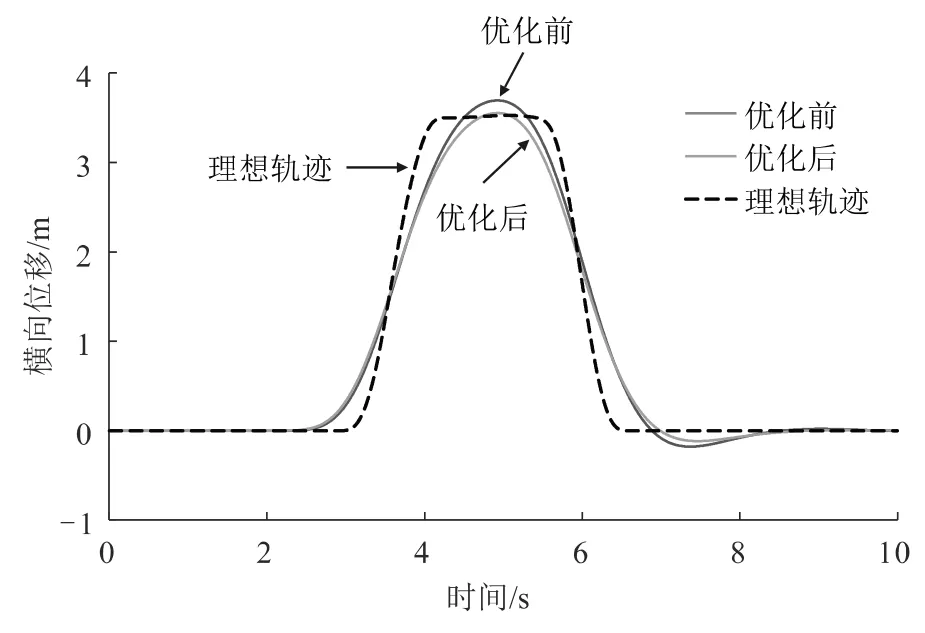
图8 双移线工况路径分析图
由图9、图10分析可知,增益值优化后传动比算法,完成同样转向动作时,横摆角速度和侧向加速度整体更小,且变化更加平稳,车辆的转向性能更好。

图9 横摆角速度结果图

图10 侧向加速度结果图
根据优化前后传动比测试结果计算综合评价值FH,如表2所示。

表2 综合评价指标值表
优化后综合指标值FH更小,车辆具有更好的稳定性。
综上,基于优化后定增益所设计的传动比,相较于优化前具有更好操纵稳定性能。
4.2 稳态回转工况
选取稳态回转工况进行测试,确定所设计传动比算法具有定增益转向特性。
固定方向盘转角dsw=30°,设置初始车速为u=20 km/h,随时间缓慢增加到u=60 km/h,运行工况t=40 s。测试结果如图11所示。

图11 稳态回转横摆角速度图
根据图11分析,在低速段由于限制了传动比算法最小值,所以当车速u<23 km/h时,传动比为定值,横摆角速度响应值随车速增加。当车速逐渐提高,具有变传动比特性,当车速变化时,横摆角速度响应不变。
仿真结果表明,所设计传动比算法使车辆横摆角速度增益值基本维持为定值。可以减轻不同车速下转向特性不同带来的驾驶员操作负担。
5 结论
(1)文章基于定横摆角速度增益法,测试车辆在不同速度及前轮转角下的车辆转向特性。选取方向盘横摆角速度增益值,根据车速与方向盘转角,设计车辆在对应条件下的离散变传动比值。根据最小二乘插值,得到在全车速与转角域下的传动比。
(2)根据转向系统物理结构限制改进传动比。仿真结果表明,传动比算法在u>23 km/h时,车辆具有恒定稳态横摆角速度增益,有效减轻驾驶员的操作负担。
(3)采用模拟退火算法,选取操纵稳定综合指标函数为能量函数,在范围[0.01,1]内对横摆角速度增益值进行优化,确定全局最优解Gsw=0.341。本文结合模拟退火优化算法,为SBW车辆定增益值确定提供一种新的方法。

