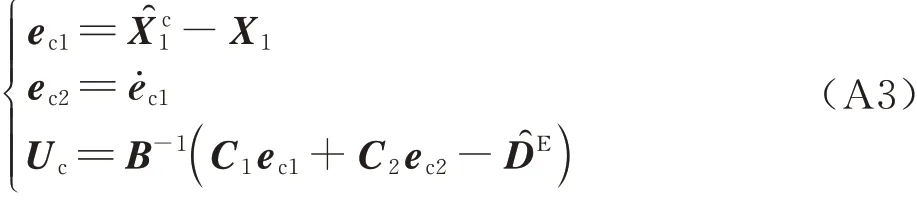伸缩套臂式无人机空基回收建模与对接控制

苏子康，徐忠楠，李春涛，陈海通，王宏伦

1．南京航空航天大学 自动化学院，南京 210016

2．北京航空航天大学 自动化科学与电气工程学院，北京 100191

近年来，小型固定翼无人机凭借其体积小、速度快的特点得到各国军界的广泛关注，并被航空发达国家用于侦察、监控、突防、打击、集群协同火力打击等军事领域［1-2］。但由于自身设计和作战使命限制，大多数小型固定翼无人机不具备远程作战能力，无法执行远程侦查、机动突防和敌后攻击等任务。即便采用大型运输机对其进行远程空基投放部署，由于远距离危险任务区域无可靠的陆基/舰基着陆平台，其在执行完任务后仍然面临无法有效回收的窘境。这不仅大大降低了其使用寿命，而且显著增加了作战成本。因此，在无可靠陆基/舰基回收平台情况下，如何采用大型空基回收平台飞机（以下称为母机）在空中进行快速、有效地回收，不仅可以实现无人机的重复使用、显著降低作战成本，而且还能为低成本无人机快速部署、机动突防、协同侦查和集群攻击等新型作战技术的发展提供技术支撑，具有重要的现实意义和可观的军事效能［3-4］。

目前以美军“小精灵”项目［5］为代表的空基回收方案主要有2种：拖曳浮标对接式回收、机械臂抓取式回收。其中，拖曳浮标对接式回收通过拖曳于母机的可收放缆绳-浮标对接锁定无人机，并由缆绳将无人机卷收回母机机舱［6-7］。该回收方式因缆绳拖曳浮标距母机较远，且采用空中柔性对接方式，可有效提高对接飞行安全，降低对接事故率和无人机损伤。但由于柔性易扰缆绳-浮标系统空中稳定性较差，使得对接过程较长，回收效率偏低。机械臂抓取式回收则是借助安装于母机的机械臂直接对稳定于期望位置的无人机进行“硬式”抓取对接，继而将其移动回收至母机机舱。相较于拖曳浮标对接式空基回收，该方式采用刚性机械臂进行直接抓取回收，避免了柔性易扰缆绳浮标系统空中稳定性差的问题，可进一步提高空基回收效率。

受启发于硬式空中加油技术［8-11］，提出了一种伸缩套臂式空基回收方法，采用嵌套伸缩机械臂结构，在中空套臂内安装可滑动伸缩臂以延长机械臂捕获距离，拓宽对接作业范围，进而在保障回收效率的同时使回收点远离母机平台，进一步降低回收风险。同时，区别于常见机械臂采用较多关节，所提伸缩套臂仅通过控制偏航、俯仰及伸缩3个关节便可实现对预对接位置处无人机的捕获回收。且各关节相互独立，避免了关节间复杂耦合，降低了运动控制难度。

然而，就伸缩套臂式空基回收而言，当前已公开文献相对较少，针对性研究有李俊国［12］提出的基于母机机腹下方伸缩臂的撞线式回收。但此项研究重点关注回收装置所受气动特性进行了分析，并未对回收控制技术展开详细研究。因此，将从与之类似的硬式空中加油伸缩套管相关方面研究现状及发展动态进行分析。针对硬式空中加油伸缩套管建模，Smith和Kunz［8］采用分离法分别构建了加油机、加油外管、加油内管模型。此外，他们还借助拉格朗日方程法构建了硬式加油系统模型［9］。对于加油管运动控制。薛建平等［10］针对加油管小扰动线性化模型，设计了H∞最优控制器进行运动控制。高久安和贾秋玲［11］则采用线性二次型调节器控制加油管跟踪目标轨迹。但以上控制方法均未能充分考虑系统内外扰动，导致系统不能迅速抑制扰动并消除跟踪误差，控制精度有待提高。而在具有相似结构的机械臂运动控制方面，此类问题得到较好的解决。姚来鹏等［13］设计了一种基于自适应终端滑模的弹药传输机械臂，实现了负载变化和非线性摩擦情况下机械臂的快速准确定位。Feng等［14］采用非奇异终端滑模控制，使机械臂控制系统能够迅速抑制扰动，实现了对多关节机械臂的精准运动控制。Zaare和Soltanpour［15］将模糊估计器与非奇异终端滑模结合，并采用自适应定律消除了模型不确定性及外界扰动影响，并在实际应用中证明了该方法的有效性。

为充分发挥伸缩套臂式空基回收优势，将借鉴上述已有研究，对其建模与对接控制技术展开深入研究。鉴于处于大型母机后方的对接回收作业区域存在母机尾涡和常值风扰持续作用。因此，如何精准地构建复杂扰流下伸缩套臂空基回收模型是首要解决的难题。而保障在上述环境扰动下依旧能够快速、精准地控制伸缩套臂与期望稳定位置处的无人机精准对接更是实现空基回收的关键性难点。所以，重点考虑针对性地解决以下技术难点：①多重复杂扰流下伸缩套臂运动非线性建模；②多重复杂扰流下伸缩套臂高精度、快速、抗干扰对接控制器设计与验证。

针对上述技术难题，借鉴硬式空中加油技术，本文构建了母机尾涡、常值风作用下的伸缩套臂仿射非线性模型。继而，为使对接控制器兼备良好的响应速度和抗扰能力，采用基于观测器的主动抗扰控制架构，研究伸缩套臂对接方法，并分析闭环系统稳定性。最后，通过仿真验证所提方法的有效性。主要创新性工作如下：

1） 相较于拖曳浮标对接式回收［6-7］，借鉴硬式空中加油技术，提出了一种新型伸缩套臂式空基回收方案，避免了柔性易扰缆绳稳定性差的问题，有效提高了空基回收效率。同时，分析了此种回收方式在母机尾涡及常值风扰流作用下的气动特性，并构建了相应仿射非线性模型。

2） 针对外界扰流和内部不可测瞬变模型项对空基对接控制性能的显著影响，设计了非奇异快速终端滑模观测器，能够更快速、准确地对扰动进行估计。

3） 采用基于观测器的主动抗扰控制架构，提出了基于非奇异快速终端滑模控制的伸缩套臂空基对接方法，弥补了相似场景下传统控制方法在响应速度上的不足，显著提高了对接控制精度、响应速度和抗扰性能。

1 问题建模

针对伸缩套臂空基回收系统结构进行介绍，并根据转动惯量质量投影法及拉格朗日方程法构建伸缩套臂仿射非线性模型。同时，采用CFD仿真软件对母机尾涡及常值风扰动综合作用下的伸缩套臂气动特性进行分析。

1.1 伸缩套臂运动学模型

受启发于硬式空中加油系统中所使用伸缩加油套管［8-9］，将回收机械臂设计为具有偏航、俯仰及伸缩三自由度的可伸缩套臂，如图1所示。该伸缩套臂主要由转动底座、可控俯仰关节、套臂、伸缩臂、机械手组成，并且整体通过固定平台安装于机舱尾部。同时，伸缩套臂各关节由液压驱动装置进行驱动，其自身的偏航及俯仰运动主要依靠转动底座和可控俯仰关节实现，伸缩运动则由液压机构驱动。

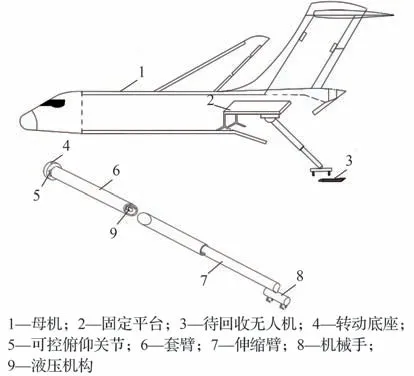
图1 伸缩套臂空基回收装置结构示意图Fig. 1 Structure diagram of telescopic boom aerial recovery device

为简化计算，便于展开后续研究，作出如下合理假设：

假设1 转动底座、套臂、伸缩臂几何外形均为规则圆柱体。

假设2 伸缩套臂各组成部件均为均质刚体，所构成伸缩套臂为刚体模型。

假设3 伸缩套臂末端机械手姿态运动的牵连影响可忽略不计，可视为质点。

假设4 所选择的对接回收区域气流较规律、平稳，可不考虑大气紊流影响。对接回收区域气流扰流主要为母机尾涡及常值风。

分别建立如图2所示的伸缩套臂偏航、俯仰及伸缩关节坐标系。其中，O0X0Y0Z0为偏航关节坐标系，其坐标原点与转动底座中心重合，Z轴方向与转动底座转轴方向重合，X轴及Y轴则分别与母机航迹坐标系X轴、Y轴平行，且坐标系整体满足右手法则；O1X1Y1Z1为俯仰关节坐标系，其坐标原点与可控俯仰关节中心重合，Z轴方向为俯仰关节转轴方向，X轴方向指向伸缩臂伸缩方向，Y轴方向依据右手法则确定；O2X2Y2Z2为伸缩关节坐标系，坐标原点位于套臂末端中心处，其各轴方向与俯仰关节坐标系各轴方向平行，且指向相同。

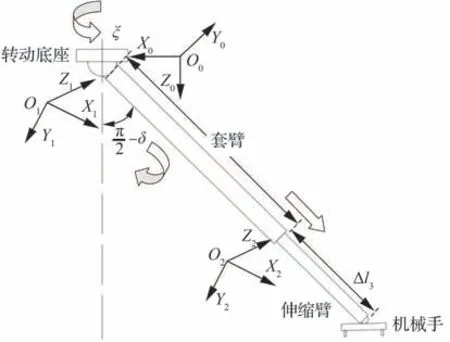
图2 伸缩套臂关节坐标系示意图Fig. 2 Diagram of joints coordinate system of telescopic boom

然后，采用齐次变换法［16］构建伸缩套臂运动学模型0Pe：

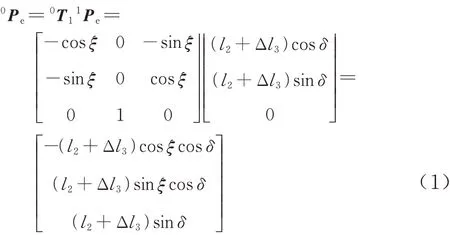
式中：1Pe为O1X1Y1Z1下末端机械手质心位置；0T1为 坐 标 系O1X1Y1Z1与O0X0Y0Z0间 变 换 矩阵；l2为套臂长度；Δl3为套臂外伸缩臂长度；δ为套臂与O0X0Y0平面夹角；ξ为套臂与O0X0Z0平面夹角。

1.2 伸缩套臂动力学模型

1.2.1 偏航关节动力学模型

对于伸缩套臂的动力学模型，可将其分为偏航和俯仰-伸缩2部分进行构建。其中，因偏航关节主要运动为驱动伸缩套臂整体绕转动底座进行旋转，故其动力学方程可表示为

式中：ω1为偏航关节角速度；τ1为偏航关节驱动力矩为伸缩套臂转动惯量，其中分别为转动底座、套臂、伸缩臂、机械手转动惯量。

式（2）中各刚体转动惯量可根据基础力学公式分别求取。其中，转动底座转动惯量I′0为式中：m1为转动底座质量；R1为转动底座底面半径。

由于套臂、伸缩臂及机械手自身与其转轴存在一定夹角（如图2），故对应转动惯量需通过转动惯量质量投影法［17］进行计算。因此，可得到

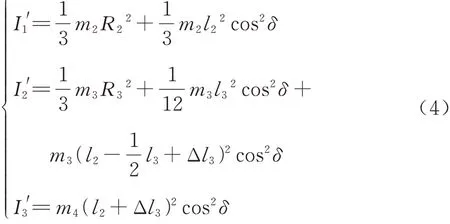
式中：m2、m3、m4分别为套臂、伸缩臂和机械手质量；R2、R3分别为套臂和伸缩臂截面半径；l3为伸缩臂长度。

由式（2）~式（4）可得伸缩套臂偏航关节仿射非线性模型如下所示：

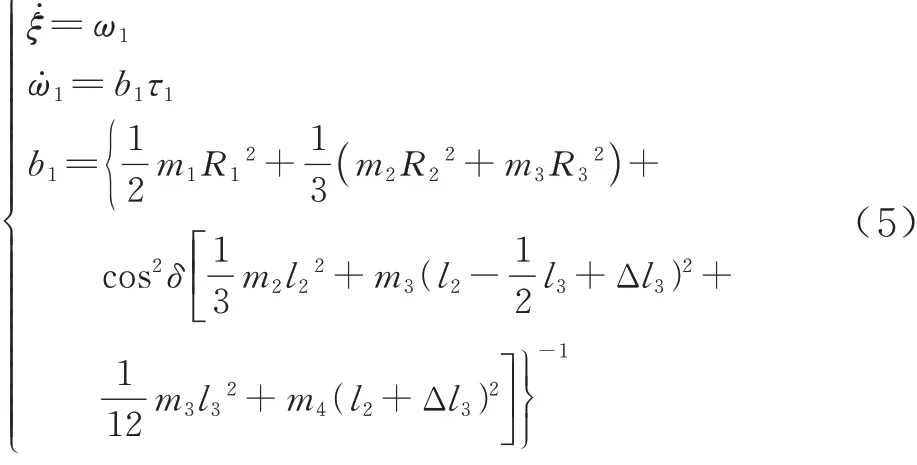
1.2.2 俯仰及伸缩关节动力学模型

俯仰关节及伸缩关节的动力学方程则可依照多关节机械臂的建模方法［18］，在不求取系统内相互作用力的情况下，借助拉格朗日方程获取。

据牛顿定理，得此部分动能Ek及势能Ep为

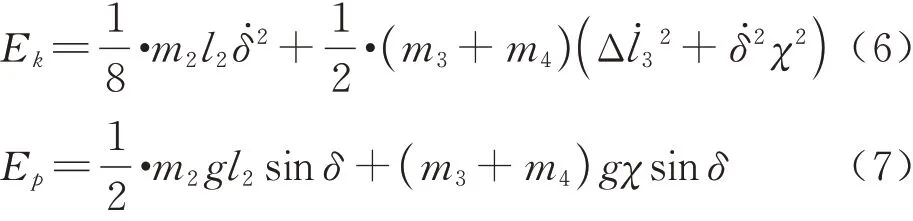
同时，定义广义坐标为q=[δΔl3]T，所以对应拉格朗日方程为

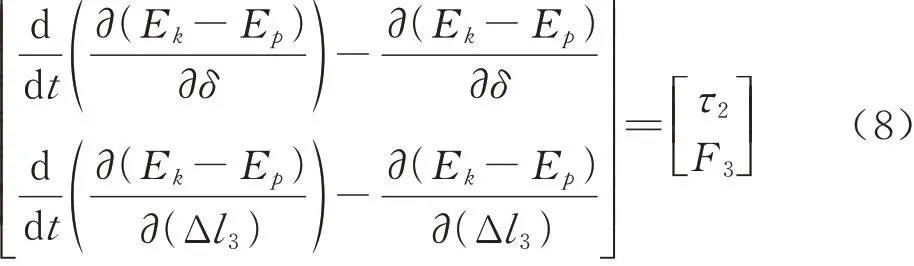
式中：τ2为俯仰关节驱动力矩；F3为伸缩关节驱动力。

至此由式（6）~式（8）可得伸缩套臂俯仰关节动力学方程式（9）及伸缩关节动力学方程式（10）：

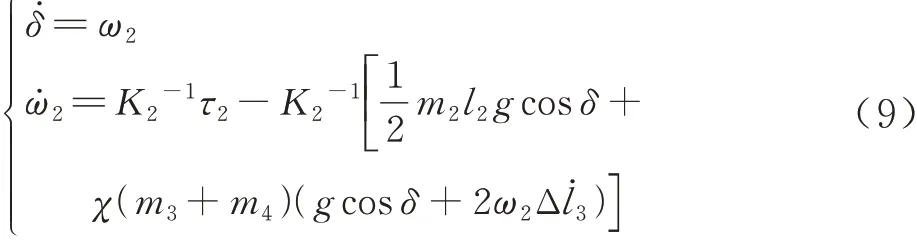
式中：ω2为伸缩套臂俯仰角速度；g为重力加速度；令K3=(m3+m4)，K2=m2(3R22+4l22)/12+，则 式（9）可 表示为

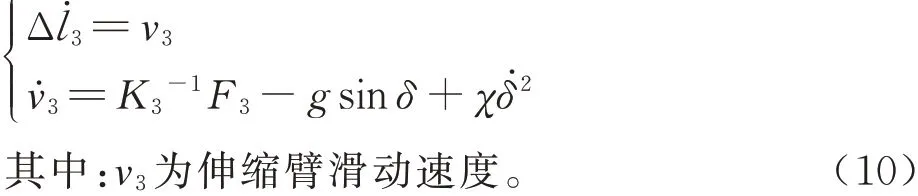
为简化模型，便于后续非线性控制设计，进一步将式（9）和式（10）中与控制输入无关且难以测量的非线性瞬变量记作关节不可测瞬变扰动，并将其改写成仿射非线性形式：

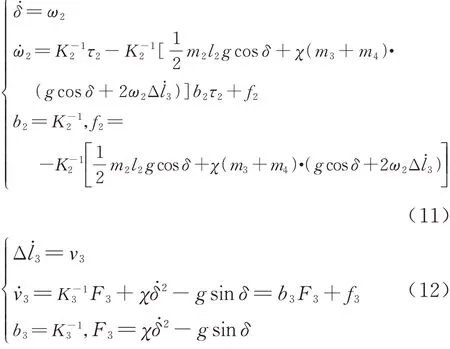
综上所述，结合式（5）、式（11）、式（12）及环境气流对伸缩套臂影响可得空基回收伸缩套臂仿射非线性模型如下所示：

式中：X1=[ξ δΔl3]T，X2=[ω1ω2v3]T均为伸缩套臂系统状态；B=diag(b1，b2，b3)，U=[τ1τ2F3]T分别为伸缩套臂系统输入矩阵及控制输入；F=[0f2f3]T为模型内不可测瞬变扰动项，主要由各关节动力学模型内与控制输入无关并且难以测量的非线性瞬变量构成；FW=[Fw1Fw2Fw3]T为伸缩套臂三通道气流扰动作用项，此项由回收区域内母机尾涡及常值风作用于伸缩套臂引起，其实质为环境扰流对关节力矩/力的干扰作用，其中，Fw1=0.5(l2+Δl3)fwsinξcosδ；Fw2=0.5(l2+Δl3)fwcosξsin2δ；Fw3=fwicosξcosδ；fw，fwi分 别为伸缩套臂及伸缩臂在环境扰流作用下气动阻力；D=[D1D2D3]T，Di(i=1，2，3)分别为系统三通道集总扰动，由模型内不可测瞬变扰动项及气流扰动作用项构成。

1.3 伸缩套臂气动特性分析

与硬式空中加油对接环境扰流类似，伸缩套臂在空基回收过程中同样会受到母机尾涡及常值风气流影响［19-20］。因此，为更准确地描述伸缩套臂在对接环境扰流下的运动特性，借助CFD软件对伸缩套臂进行气动特性分析。具体步骤如下：

步骤1 非结构化网格划分。构建伸缩套臂三维模型，并分别在偏航、俯仰及伸缩关节处设置坐标系及运动约束，使各关节可进行相应运动。同时，采用ICEM CFD软件围绕伸缩套臂建立外流场计算域，并针对计算域及伸缩套臂进行非结构化网格划分［21］。

值得注意的是，由于末端机械手相较于伸缩套臂整体而言，体积较小且形状不规则，因此，在进行网格划分时需对机械手进行加密处理，以提高网格整体质量。图3为伸缩套臂在偏航0°、俯 仰36°，伸 缩 臂 伸 出3.5 m时 网 格 划 分结果。

图3 ξ=0°，δ=36°，Δl3=3.5 m时伸缩套臂及外流场计算域网格划分结果Fig. 3 Grid division results of telescopic boom and out⁃flow field calculation domain atξ=0°，δ=36°，Δl3=3.5 m

步骤2 Fluent计算处理。借助Fluent软件对所划分网格进行迭代计算，并根据计算结果分析伸缩套臂在气流扰动作用下的气动特性。

值得注意的是，为考虑空基回收环境下流体压缩性的影响，选取隐式耦合求解器，并选用SA（Spalart-Allmaras）湍流模型进行求解计算。同时，设置仿真计算边界条件为压力远场（Pressurefar-field），在理想气体条件下，设置条件参数为马赫数Ma=0.3，并根据伸缩套臂当前姿态受常值风及尾涡等效风综合作用，确定笛卡尔坐标系内来流方向及大小，如表1所示。其中，尾涡等效风速通过等效气动效应法对Hallock-Burnham尾涡模型下伸缩套臂所受影响进行线性平均求和获取［19］。图4和图5分别为伸缩套臂在偏航0°、俯仰36°，伸缩臂伸出3.5 m时的外围压力云图和速度矢量图。

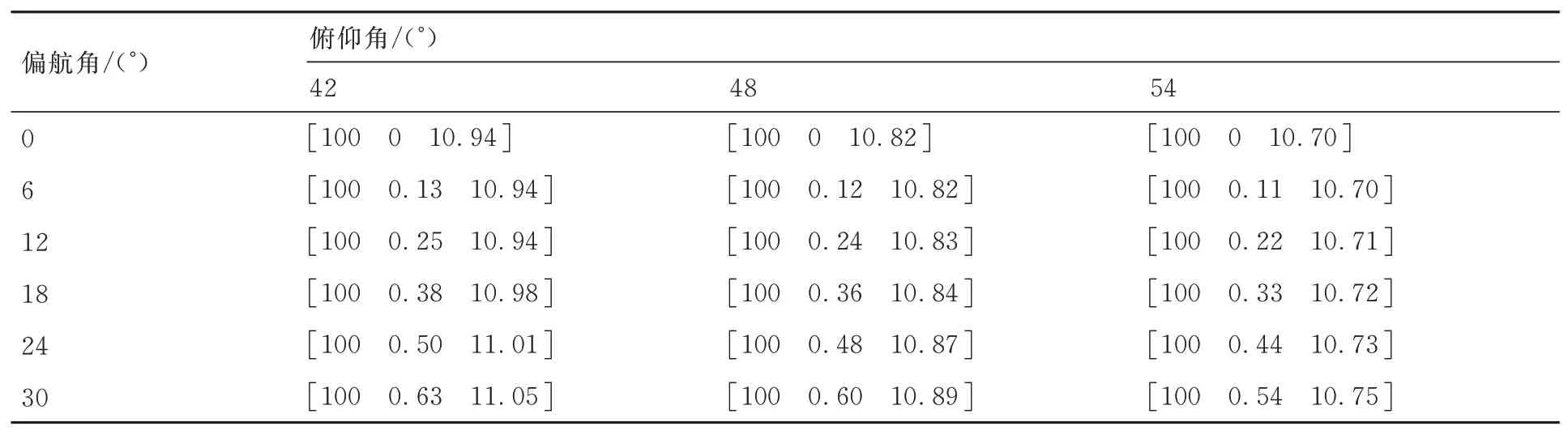
表1 笛卡尔坐标系下各方向来流大小Table 1 Magnitude of flow in cartesian coordinates

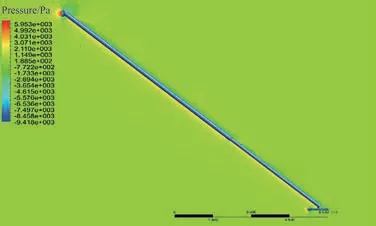
图4 ξ=0°，δ=36°，Δl3=3.5 m时计算结果压力云图Fig. 4 Pressure cloud diagram of calculated results atξ=0°，δ=36°，Δl3=3.5 m

图5 ξ=0°，δ=36°，Δl3=3.5 m时计算结果速度矢量图Fig. 5 Velocity vector diagram of calculated results atξ=0°，δ=36°，Δl3=3.5 m

步骤3 不同姿态/长度下气动分析与数据处理。调整步骤1中各关节运动约束参数，改变伸缩套臂姿态和长度，并重新进行网格划分和尾涡等效风速计算。同时对新姿态下的网格进行Fluent计算处理，分析其气动特性。重复以上操作，进而得到多组特定姿态下的伸缩套臂气动数据。在后续控制设计仿真验证中通过对其进行线性插值，获得不同俯仰角、偏航角及伸缩长度下的伸缩套臂气动数据。图6为伸缩臂伸出长度为3.5 m时，不同俯仰角及偏航角下伸缩套臂所受阻力大小情况。

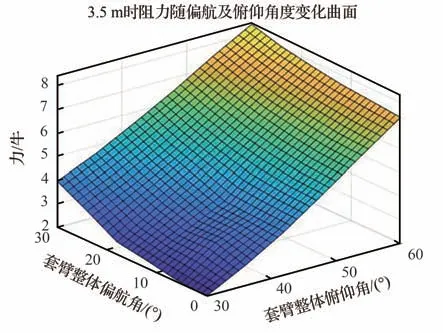
图6 Δl3=3.5 m时阻力随俯仰角及偏航角变化曲面Fig. 6 Surface diagram of variation of resistance of tele⁃scopic boom with pitch and yaw angle at Δl3=3.5 m

2 空基回收对接控制设计

为在环境扰流作用下实现伸缩套臂的快速准确高抗扰对接控制，采用干扰观测技术［22］（Disturbance Observer， DO），针对伸缩套臂偏航、俯仰及伸缩三通道分别构建非奇异快速终端滑模观测器（Nonsingular Fast Terminal Sliding Mode Observer，NFTSMO），以重构各通道集总扰动，并在此基础上，设计了非奇异快速终端滑模控制器［23-26］以提高控制精度，加快响应速度。图7为所提出的伸缩套臂非奇异快速终端滑模对接控制（Nonsingular Fast Terminal Sliding Mode Control，NFTSMC）方 法 控 制结构。

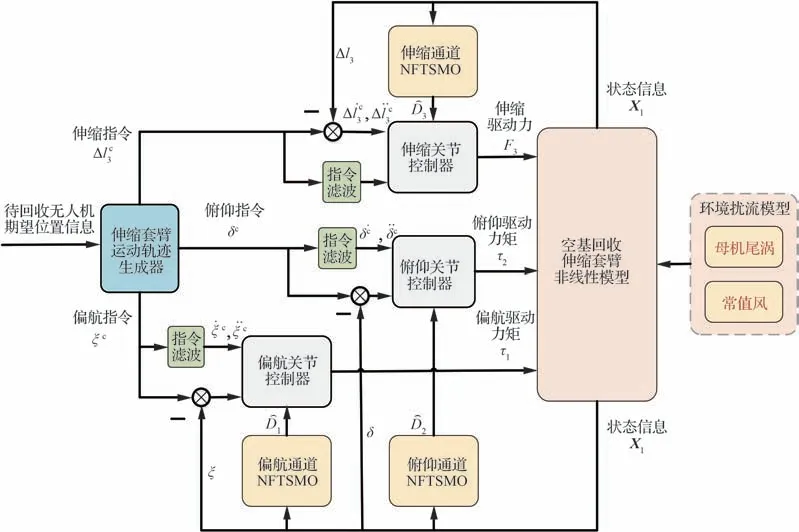
图7 伸缩套臂非奇异快速终端滑模对接控制方法Fig. 7 Nonsingular fast terminal sliding mode control method of telescopic boom

2.1 对接引导轨迹设计

在空基回收过程中伸缩套臂需平滑地驱使末端机械手靠近待回收无人机，因此，采用sigmoid函数构建伸缩套臂对接引导轨迹［27］。需要注意的是，由于伸缩套臂为刚性体，当末端机械手位置确定时，伸缩套臂姿态也相应确定。所以，对接引导轨迹设计主要针对末端机械手位置变化展开。

记机械手在O0X0Y0Z0坐标系内起始位置为P0=[x0y0z0]，终 端 目 标 位 置 为Ps=[xsyszs]，则采用sigmoid函数可设计机械手在Z轴方向上的位置引导指令函数z(t)为

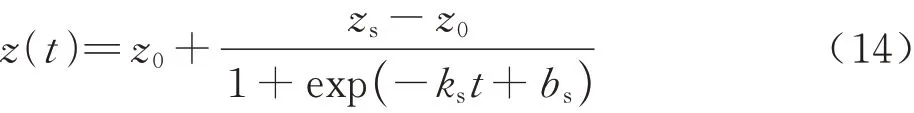
式中：t为时间变量；ks为时间常数；bs为时间偏移量。

以z(t)为时间基准进一步设计机械手在X，Y方向上多项式形式的轨迹引导指令函数，并根据起始位置P0及目标位置Ps求取其系数。至此，可得到伸缩套臂机械手轨迹引导函数：

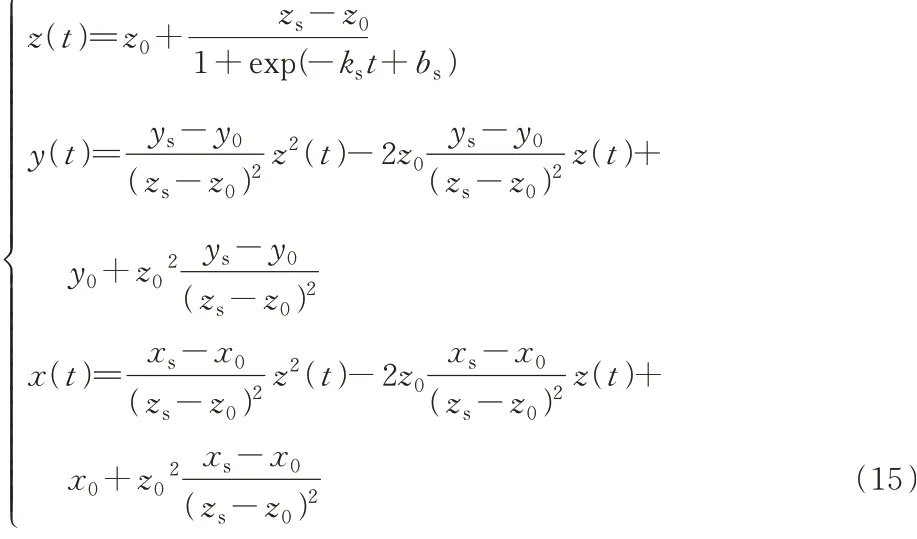
而实际采用的对接引导轨迹式（16）则需进一步对伸缩套臂运动学模型式（1）进行逆运动学求解，并结合式（15）获得。值得注意的是，引导轨迹式（16）中伸缩套臂偏航角及俯仰角取值范围分别为在该范围下伸缩套臂运动学逆解均存在，运动轨迹不存在奇点。

2.2 伸缩套臂运动干扰估计

针对伸缩套臂三通道中扰流关联项和不可测瞬变模型扰动构成的系统集总扰动，设计了NFTSMO，以重构各通道集总扰动。

如式（13）所示，NFTSMO主要对伸缩套臂所受扰流作用及动力学模型中不可测瞬变扰动构成的系统集总扰动D进行估计。基于前文集总干扰建模分析及NFTSMO设计中关于干扰假设［23-24］，对集总扰动D作如下假设：

假设5［14］系统集总扰动D连续可导且满足为系统扰动限定值，l>0。

根据式（13），设计NFTSMO如式（17）：

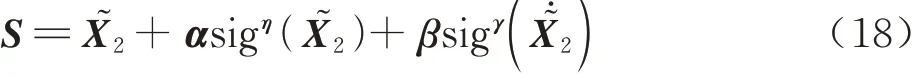
式中：S=[s1s2s3]T为三通道滑模面向量；分别为对应滑模面系数，且满足αi>0，βi>0，1<γi<2，γi<ηi（i=1，2，3）；sig(⋅)为新定义函数。对于向量

为使NFTSMO在观测过程中更加快速稳定地抵达滑模面式（18），进一步设计滑模趋近率：

式 中：Q=diag(Q1，Q2，Q3)，J=diag(J1，J2，J3)，σ=[σ1σ2σ3]分别为滑模趋近率系数，且满足Qi>0，Ji>0，0<σi<1（i=1，2，3）； sigσ(S)=

由NFTSMO式（17），滑模面式（18）和趋近率式（19），可设计观测器控制输入式（20）为

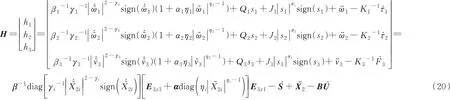
式中：E3x3=diag(1，1，1)；E3x1=[1 1 1]T；则分别对应

2.3 伸缩套臂控制器设计

为使伸缩套臂能够迅速响应控制信号，精准跟踪目标轨迹，采用非奇异快速终端滑模技术［24-25］对控制器进行设计。

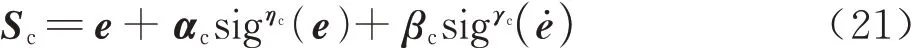
式中：Sc=[sc1sc2sc3]T为控制器滑模面向量；αc=diag(αc1，αc2，αc3)，βc=diag(βc1，βc2，βc3)，ηc=[ηc1ηc2ηc3]，γc=[γc1γc2γc3]分 别 为控制器三通道滑模面系数，且满足αci>0，βci>0，1<γci<2，γci<ηci（i=1，2，3）；sigηc(e)=

同时，为进一步提升控制器抵达滑模面的收敛速度，设计趋近率为

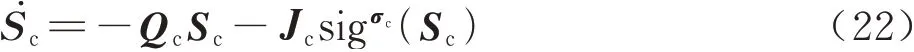
式 中：Qc=diag(Qc1，Qc2，Qc3)，Jc=diag (Jc1，分别为 滑 模 控制器趋近 率系数，且满足Qci>0，Jci>0， 0<σci<1（i=

最终，可设计滑模控制量式（23）为

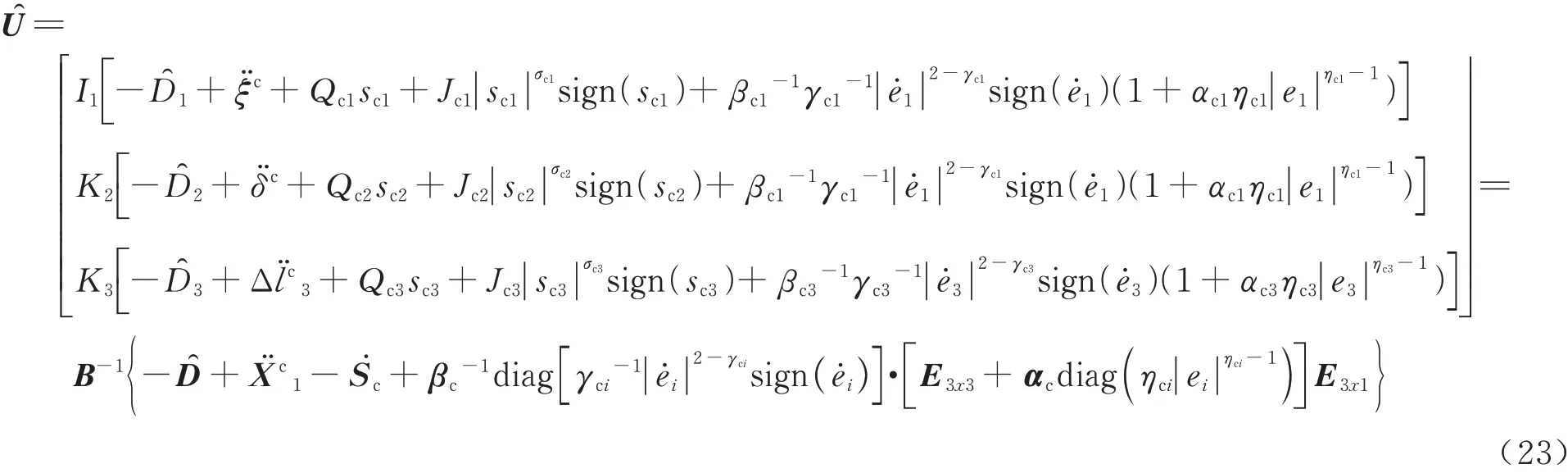
式中：i=1，2，3。

值得注意的是，所设计控制器中各通道指令输入及其微分信号可通过指令滤波式（24）获取［26］：

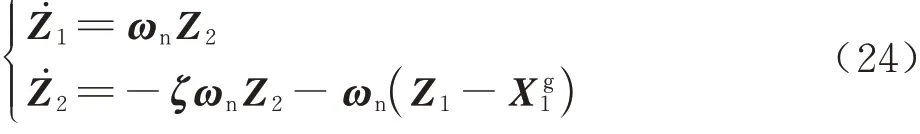
2.4 闭环稳定性分析

本节将结合2.3节所设计干扰观测器及对接控制器对伸缩套臂高抗扰对接控制系统闭环稳定性进行分析。

引理1 存在扩展Lyapunoy函数在有限时间内收敛，当Lyapunoy函数满足以下不等式［24］：

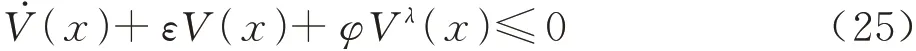
式中：ε>0，φ>0，0<λ<1。

进一步假设xv为系统初始状态，则系统状态在有限时间tv内收敛为0，其中：

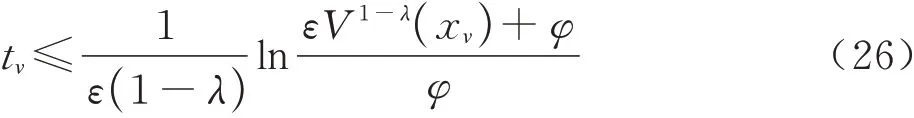
定理1 对于NFTSMO式（17），设计滑模面式（18）及趋近率式（19），则对给定观测器输入式（20），选取合适滑模面式（18）、趋近率式（19）及指令滤波器式（24）参数，可确保估计误差及有限时间内收敛为0。

证明对于NFTSMO稳定性，采用Lyapu⁃noy方程式（27）进行证明：

由干扰观测器对应滑模面式（18）推导得式（27）导数为

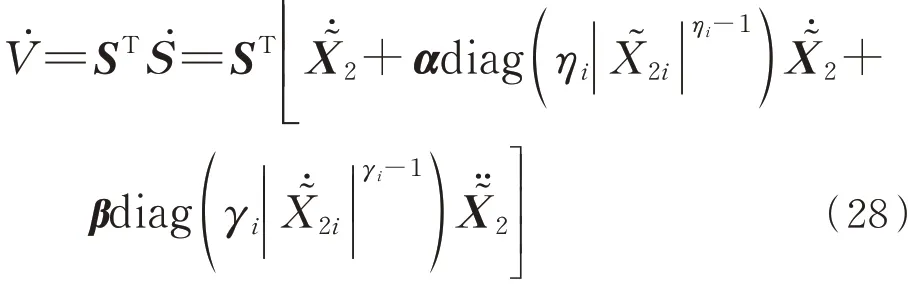
式中：i=1，2，3。

并且根据观测器式（17）及其控制输入式（20）可进一步得到：

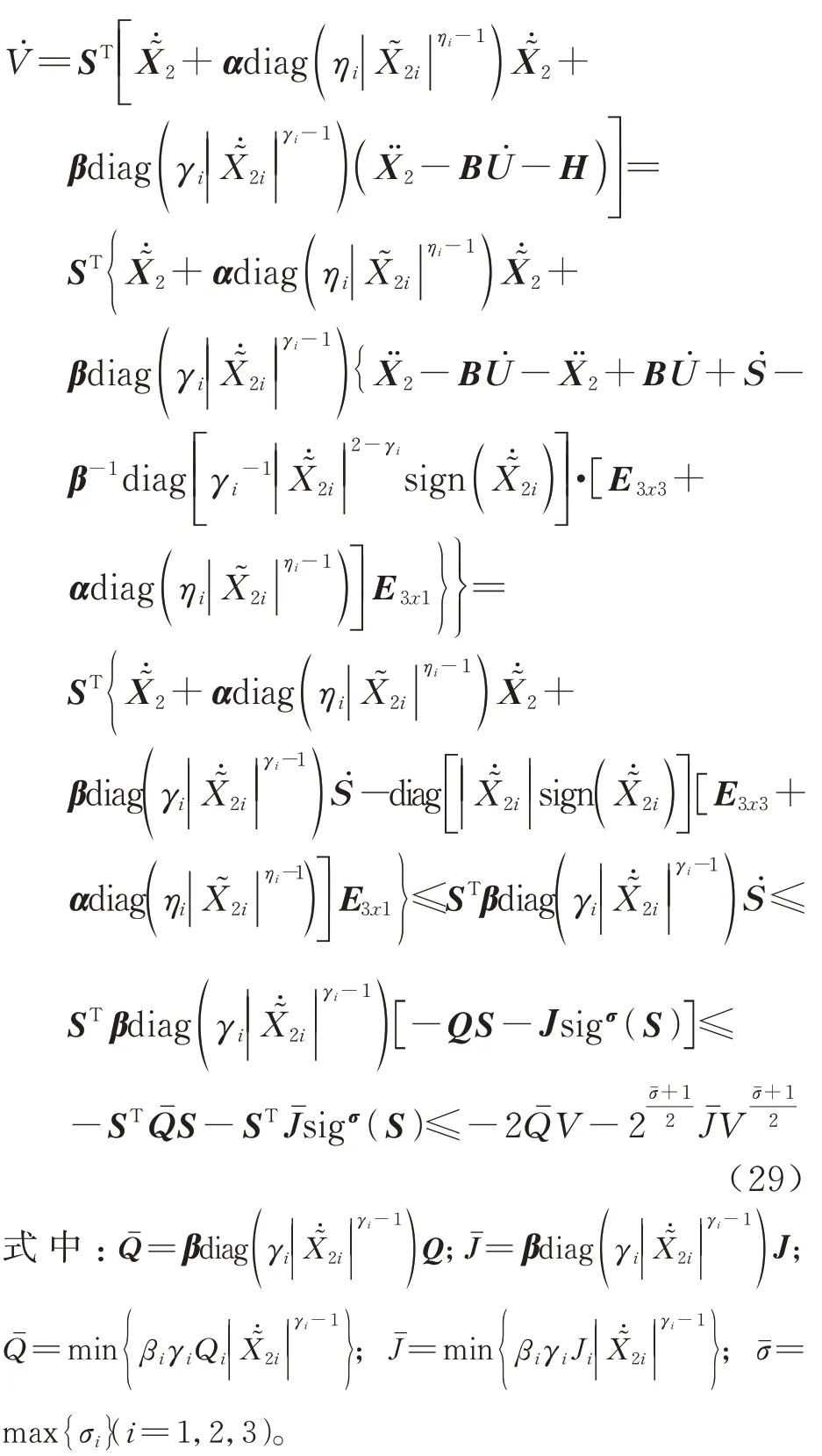
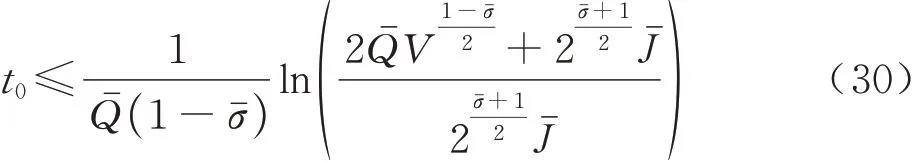
所以设计的观测器可在有限时间内准确估计模型的集总扰动。

证毕。■

定理2 针对伸缩套臂高抗扰对接控制系统，根据伸缩套臂三通道仿射非线性模型式（13）、NFTSMO式（17）及观测器输入式（20），设计滑模面式（21）及趋近率式（22），则对给定滑模控制量式（23），通过选取合适滑模面式（21）及趋近率式（22）参数，可确保跟踪误差ei(i=1，2，3)有限时间内一致收敛。

证明对于伸缩套臂高抗扰对接控制系统稳定性，选取Lyapunoy方程式（32）进行证明：

根据控制器滑模面式（18）对式（32）进行求导，可得：

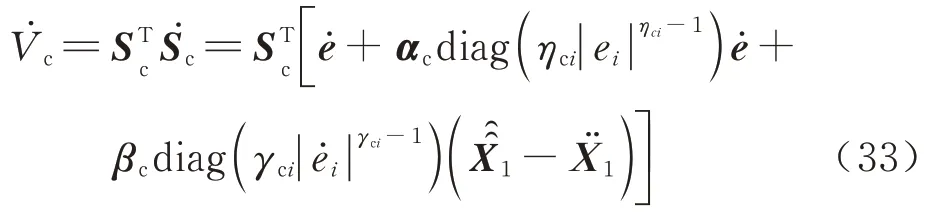
同时以滑模控制量式（23）为各通道控制输入，结合伸缩套臂模型式（13）可知：

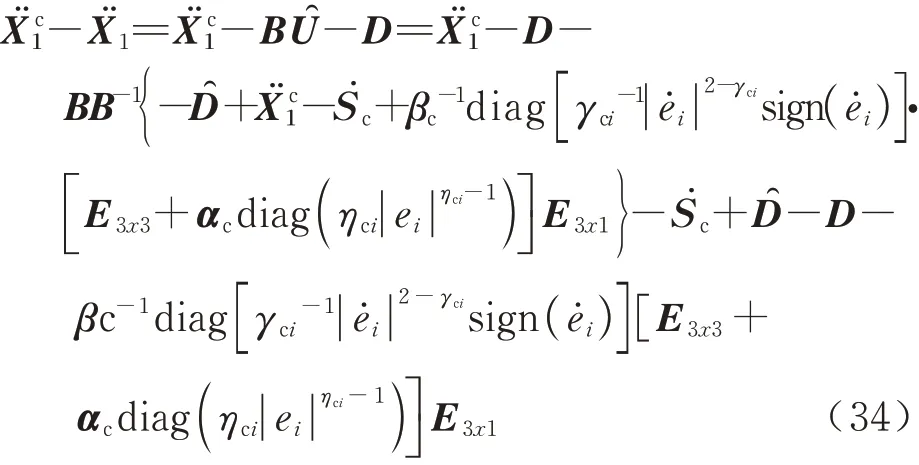
进一步将式（34）代入式（33）可得：

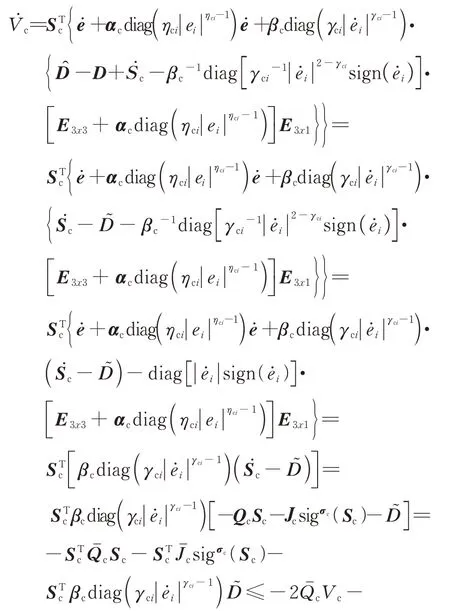
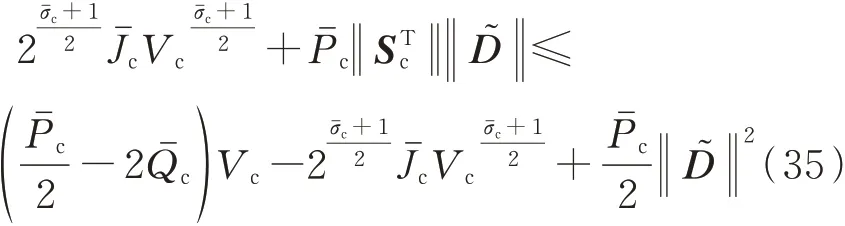
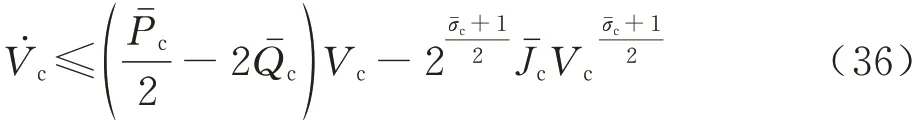
因此，根据引理1可知，所设计基于非奇异快速终端滑模技术的伸缩套臂高抗扰对接控制系统各控制回路均收敛，系统闭环稳定。

证毕。■

3 仿真验证与分析

基于构建的伸缩套臂非线性模型，借助Matlab仿真软件对所提对接控制方法的有效性进行数字仿真验证分析。假设对接过程中安装有伸缩套臂的母机作定直平飞运动，飞行高度H0=7 000 m，飞行速度V0=100 m/s，质 量 为136 000 kg，翼 展 为39.88 m，并且所安装伸缩套臂几何参数如表2所示。

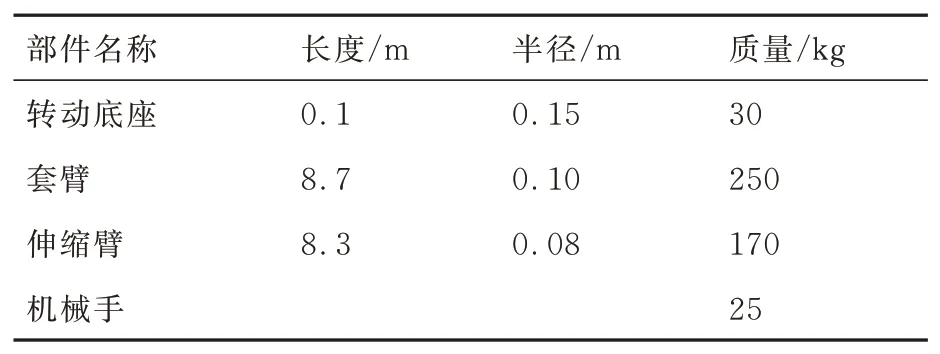
表2 伸缩套臂各部分参数Table 2 Parameters of each part of telescopic boom

同时，此次仿真中选取伸缩套臂状态X1初始值为目标值为则由运动学方程式（1）可知对应末端机械手质心位 置 分 别 为P0=[−8.25 4.76 5.50]，Ps=[−12.02 0 12.02]。因此，结合式（15）可得仿真过程中末端机械手运动轨迹为

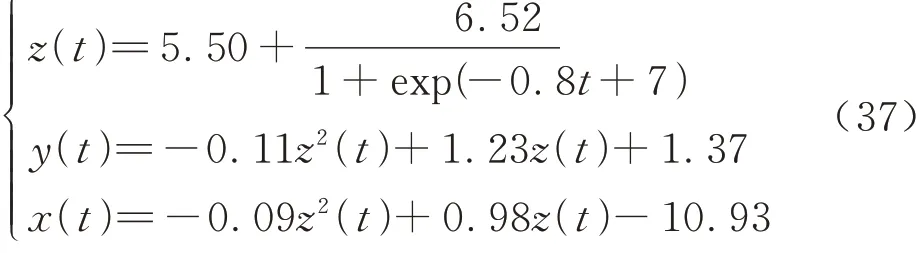
结合1.3节所得伸缩套臂气动数据，通过线性插值将目标轨迹下母机尾涡及常值风影响作用于伸缩套臂模型。同时，为验证所提对接控制方法的有效性及控制性能，与现有抗扰控制方法进行对比。考虑到伸缩套臂对接控制相关研究较少，为尽量确保对比的相对公平性，选取同样具有干扰观测器—扩张状态观测器（Extended State Observer， ESO）的 自 抗 扰 控 制（Active Distur⁃bance Rejection Control， ADRC）方法［28］进行对比，其具体公式见附录A。2种控制方法下各通道观测器及控制器对应参数设置如表3所示。

表3 伸缩套臂各控制回路参数Table 3 Parameters of telescopic boom control loop

图8~图15为上述参数配置下对接控制仿真结果。其中，图8和图9分别为各关节集总扰动估计及估计偏差。由图8可知，对接过程中伸缩套臂各关节集总扰动均以较快速度变化，且ESO及NFTSMO均能较好地进行估计。并且结合图9中各观测器估计偏差可知，相较于ESO，NFTSMO扰动估计精度更高，估计偏差更小。因此，本文所设计NFTSMO对伸缩套臂各关节不可测瞬变集总扰动具有更好的估计效果。

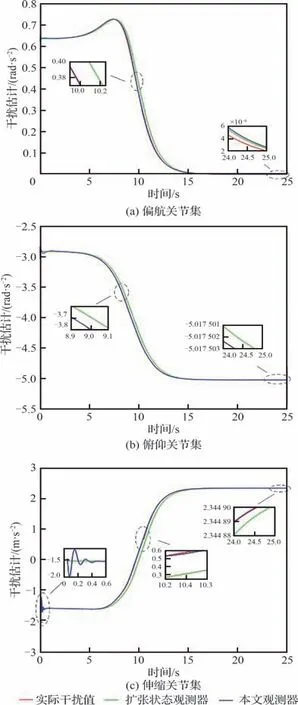
图8 各关节集总扰动估计Fig. 8 Estimation of lumped disturbances of telescopic boom

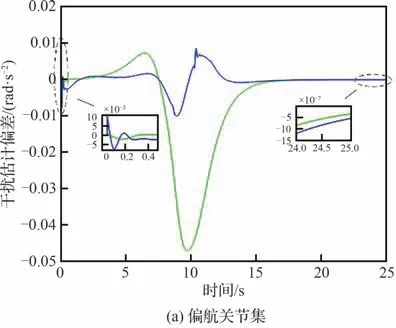
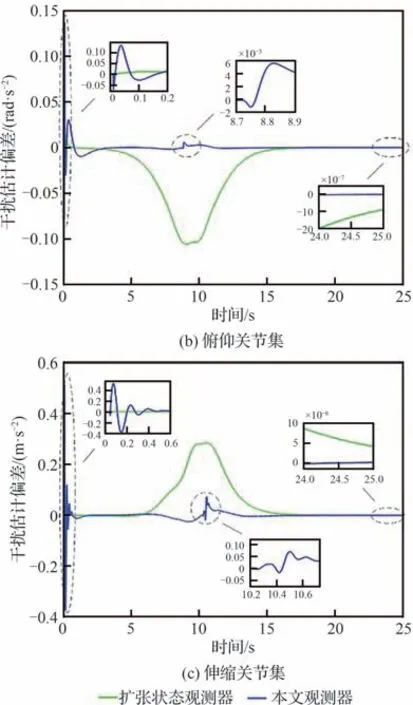
图9 各关节集总扰动估计偏差Fig. 9 Estimation deviations of lumped disturbances of telescopic boom joints

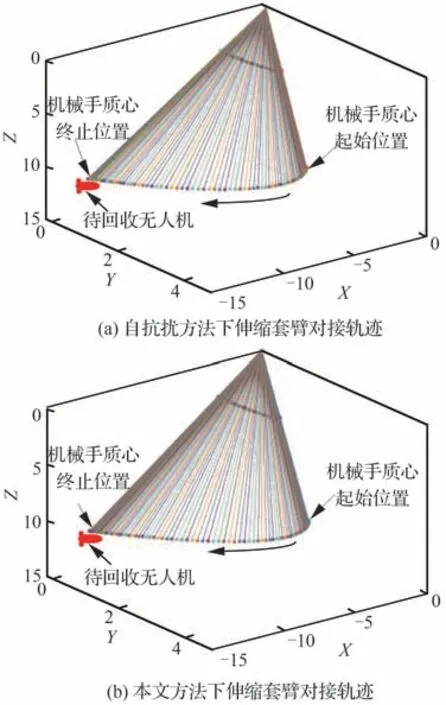
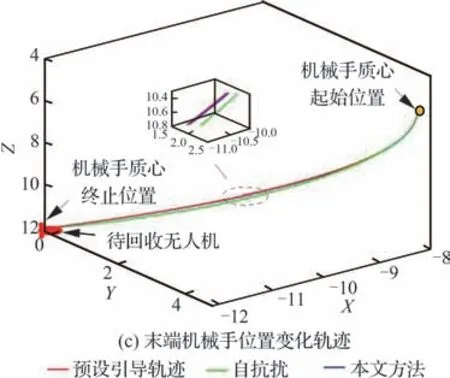
图10 伸缩套臂运动轨迹变化Fig. 10 Changes of movement trajectory of telescopic boom

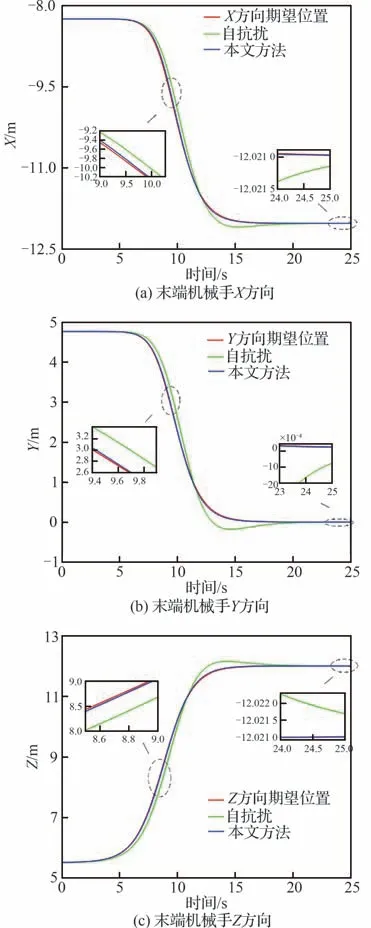
图11 伸缩套臂末端机械手位置变化Fig. 11 Position change of telescopic boom manipulator

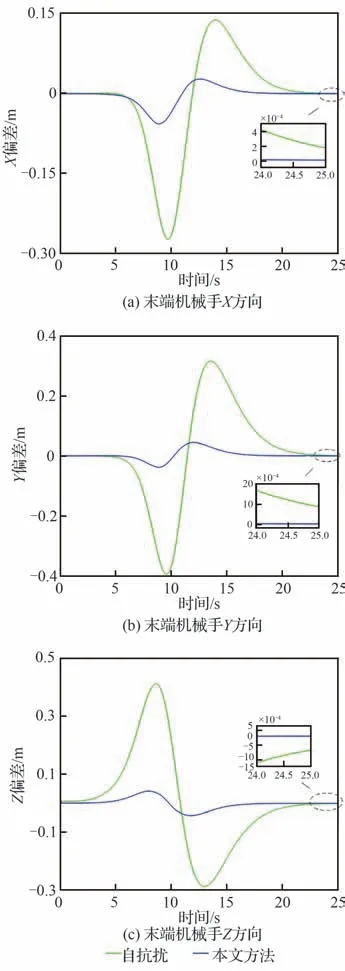
图12 末端机械手实际位置与期望位置偏差Fig. 12 Position deviation of the manipulator

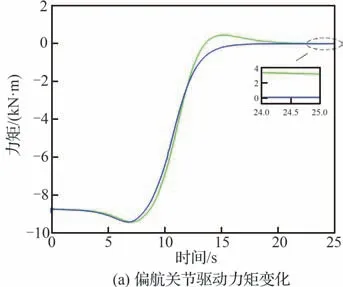
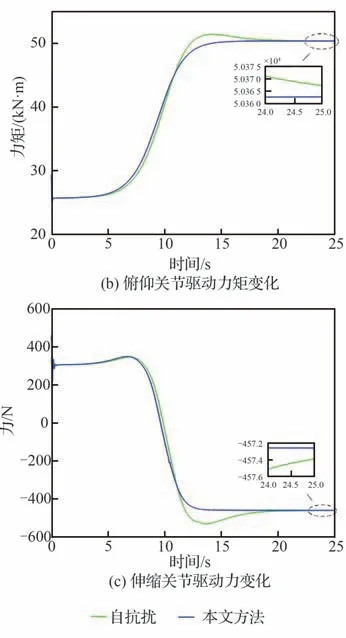
图13 伸缩套臂关节驱动力矩/力Fig. 13 Control torque/force of the telescopic boom

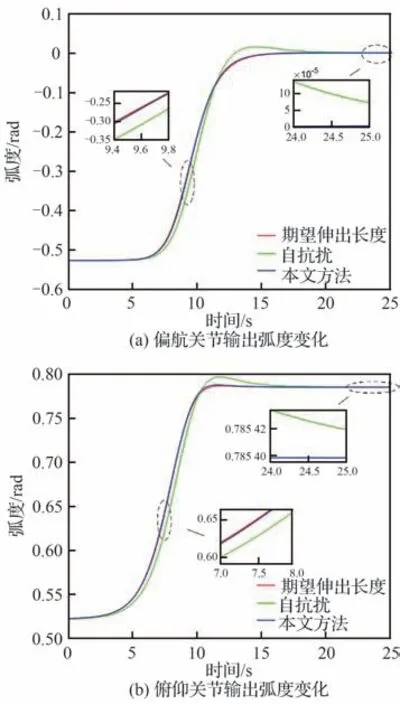
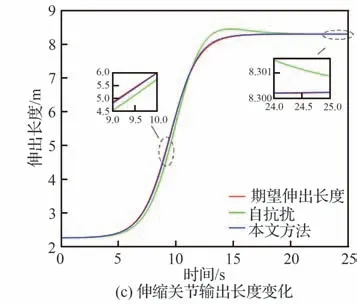
图14 各关节实际状态变化情况Fig. 14 State changes of telescopic boom joints

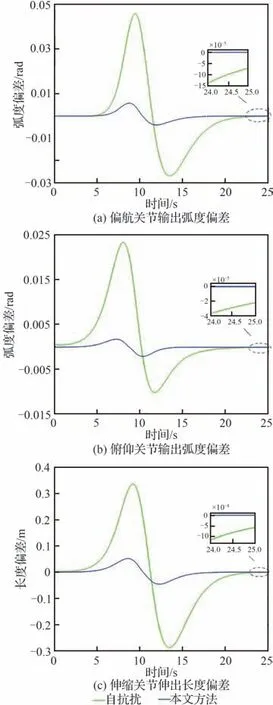
图15 各关节实际输出与期望输出间偏差Fig. 15 Output deviation of telescopic boom joints

对于所设计NFTSMC方法整体控制效果，则可通过图10~图15进行分析。其中，图10（a）和 图10（b）分 别为ADRC及NFTSMC方法下 伸缩套臂对接轨迹变化情况，图10（c）为伸缩套臂末端机械手运动轨迹。图11和图12则分别为运动过程中机械手位置变化及偏差情况。图13为ADRC及NFTSMC控制方法下伸缩套臂关节控制力矩/力变化情况，图14和图15则分别为2种方法下各关节输出弧度/长度变化情况及其与目标值间偏差。

由 图10（a）、图10（b）可 以 看 出，ADRC及NFTSMC方法均可控制伸缩套臂跟踪目标轨迹使其平滑地完成对接运动。但进一步结合图10（c）、图11、图12发 现，相 较 于ADRC，NFTSMC方法下末端机械手运动轨迹更接近目标轨迹，轨迹跟踪效果更好。并且，采用NFTSMC方法使得末端机械手在各方向上位置与期望位置偏差更小，系统收敛速度更快。尽管如此，2种方法均在10 s前后依旧存在明显偏差。而上述偏差产生原因可根据图13~图15进一步细致分析。

从图13中可以看出，在仿真时间10 s前后伸缩套臂关节力矩/力均迅速变化，且图14中对应各关节状态也快速变化。同时结合图9和图15可知，该时刻各关节集总扰动估计及输出均存在明显偏差。因此可知，对接过程中因伸缩套臂快速运动，观测器及控制器响应较慢，在系统内不可测扰动及外界风扰作用下，致使控制器未能精准补偿扰动并控制关节驱动力矩/力使其各关节输出与期望输出保持一致，从而导致末端机械手位置未能精准跟踪期望位置。但由以上仿真结果表明，相较于传统ADRC方法，NFTSMC方法下观测器及控制器响应速度更快，干扰估计及跟踪误差更小。因此，在考虑外界环境扰流下所设计的基于非奇异快速终端滑模技术的控制方法可使伸缩套臂各关节快速响应控制信号，实现较为精准地运动控制，具有较好的控制效果。

4 结论及展望

1） 借鉴硬式空中加油技术，提出了伸缩套臂式空基回收方案，构建了伸缩套臂仿射非线性模型，并分析了该模型在母机尾涡及常值风作用下的气动特性，为后续开展伸缩套臂运动控制设计奠定了模型基础。

2） 考虑到空基回收过程中存在环境扰流及伸缩套臂自身模型内不可测量瞬变扰动的影响，设计了三通道非奇异快速终端滑模干扰观测器，准确重构了系统不可测量集总扰动。

3） 结合干扰观测技术和快速终端滑模控制技术，提出了一种伸缩套臂非奇异快速终端滑模高抗扰精确快速对接控制方法，并分析了系统闭环稳定性。

4） 通过数值仿真对比分析了所提出的伸缩套臂对接控制方法的有效性。验证了所提对接控制方法具有更高的控制精度、更快的响应速度和更好的抗扰性能。

所提出的新型伸缩套臂式空基回收方案，相关研究目前尚处于初级阶段。后续将进一步考虑空基回收中待回收无人机受内外环境扰动问题，更深层次地开展伸缩套臂与无人机的协作对接控制研究，以实现无人机快速回收。

附录A：

伸缩套臂对接控制系统扩张状态观测器：

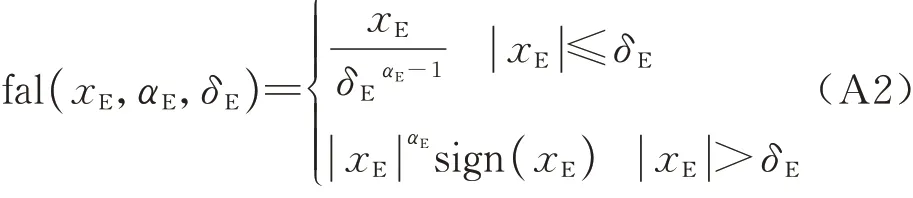
伸缩套臂对接控制系统自抗扰控制器表示为