基于改进波长调制光谱技术的高吸收度甲烷气体测量*
李绍民 孙利群
(清华大学精密仪器系,精密测试技术及仪器国家重点实验室,北京 100084)
本文对波长调制光谱(WMS)技术进行了改进,并以其为基础测量了高吸收度的甲烷气体.WMS 常被用于气体浓度测量,其依赖于二次谐波幅值与气体浓度之间的线性关系,但是传统的WMS 技术只适用于气体吸收度远小于1 的情况,这是因为在传统WMS 理论的推导中,需要对朗伯比尔定律进行一阶近似,而一阶近似仅在低吸收度下成立,所以在高吸收度下二次谐波与气体浓度的线性关系不成立.在本文的改进方案中,不需要对朗伯比尔定律做任何近似处理.将激光分为测量光与参考光两路,测量光被待测气体充分吸收后由光电探测器收集光强信号,参考光的光强信号不被吸收直接由另一个光电探测器直接探测,两个光电探测器的输出信号经模数转换后传输至上位机,上位机对两路信号均先取自然对数,然后根据参考信号确定二次谐波的解调相位,这样解调出来的二次谐波信号即使在高吸收度下也与气体的浓度保持线性关系.本文介绍了传统WMS 理论与改进后的WMS 理论,并分别测量了一系列浓度梯度的甲烷气体,对比了传统WMS 和改进WMS 的实验结果,证实了在高吸收度下,传统WMS 理论中的线性不再成立,但改进的WMS 仍能保证二次谐波与甲烷浓度之间的线性关系,验证了改进方案的优势;最后通过艾伦标准差分析,得到该甲烷测量系统在平均时间103.6 s 时稳定性达到最优,对应的艾伦标准差为26.62×10—9 分之一体积.
1 引 言
甲烷是一种重要的工业气体,在现代化工与能源领域发挥不可替代的作用[1−3],然而它易燃易爆,一旦泄露则会有非常大的安全隐患;同时它也是一种重要的温室气体[4],它的暖化能力是二氧化碳的数十倍[5],所以对甲烷气体浓度的测量对安全生产与环境保护都有重要意义.而波长调制光谱(wavelength modulation spectroscopy,WMS)作为一种高灵敏度、低噪声、低成本、实时性高、稳定性佳的光学测量手段[6−9],是一种常用的甲烷浓度测量技术[10−13].WMS 是可调谐半导体激光吸收光谱(tunable diode laser absorption spectroscopy,TDLAS)的重要分支,因其诸多优势,被广泛应用于诸多领域,比如呼吸诊断[14,15]、大气成分检测[16,17]、燃烧诊断[18,19]等.WMS 技术的起源可以追溯到20 世纪70 年代,研究人员通过探测吸收信号的一次谐波来提高测量的信噪比[20].经过近半个世纪的发展,WMS 的理论已经比较完善,根据测量原理层面的区别,可将WMS 划分为两类: 一类是传统WMS,另一类是免标定的WMS[21−23].传统WMS 通常依赖于二次谐波(2f)幅值与待测气体浓度之间的线性关系,需要事先使用一系列浓度梯度的标准气体对系统进行线性标定[24].在传统WMS 理论推导中,须对朗伯比尔定律进行一阶近似,于是气体的吸收项从e 的指数项变成了线性项,这是2f与气体浓度呈线性的关键,但也限制了其应用场景,即只能测量低吸收度气体,在高吸收度下一阶近似不再成立.免标定WMS 的基本思想是用理论仿真的谐波与实际测量的谐波进行拟合,当二者之间的残差最小时即可认为仿真中的气体吸收参数为真实值[25].免标定WMS 理论上适用于任何吸收度,并且可以同时测量气体的温度、压强、浓度等多种参数,但它需要额外的硬件设备实时监测激光的调谐参数,而且需要比较耗时的多变量拟合过程,通常用于气体所在环境的温度和压强不确定或剧烈变化的情况之下,比如内燃机和火焰的燃烧过程[26].
本文以传统WMS 技术为基础,提出了一种改进方案.在此改进的WMS 理论中,不需要对朗伯比尔定律进行任何低阶近似,而需要对其取自然对数,这样一来气体的吸收项就也变成了线性项,与传统WMS 中的一阶近似效果相同.但不同的是,非近似的处理方法能够摆脱低吸收的限制,即使在高吸收度下也严格成立.在实际操作层面,激光的调制方式与传统WMS 无异,调制信号同样是由低频锯齿波(或三角波)与高频(kHz 量级)正弦波叠加而成,在实验装置上则需将激光分为参考光与测量光两路,参考光直接用光电探测器探测,而测量光先被气体吸收后再被另一个光电探测器探测,两个探测器的输出信号被双通道ADC 转换后输入上位机,上位机对两通道信号均取自然对数.在解调吸收信号的二次谐波之前,首先借助参考信号确定二次谐波的解调相位,之后解调得到吸收信号的二次谐波,这样得到的2f与气体浓度之间的线性关系不受低吸收度的限制,相较于传统WMS 技术有更大适用范围.
在理论部分,以对照的方式详细推导了传统WMS 与改进WMS 的核心公式,凸显它们的异同点;在实验部分,用体积比为100.9×10—6,500.9×10—6,1002×10—6,2996×10—6,6960×10—6和 10510×10—6共6 种不同浓度的甲烷气体进行了实验.实验中采用了光程为8 m 的怀特型气体吸收池,根据HITRAN 数据库[27]中甲烷的吸收系数,计算得到实验中甲烷气体的吸收度约为0.024—1.78.实验对比了传统WMS 和改进方案的测量结果,正如理论分析所示,传统WMS 无法在高吸收度下保持二次谐波信号与浓度之间的线性关系,而改进后的WMS 仍表现出良好的线性.根据艾伦标准差分析,估计该甲烷测量系统的噪声水平最低约为1/26.62×10—9体积.本文提出的改进方案可用于测量高浓度气体或气体浓度有很大变化范围,比如监测空气中的水蒸气含量、矿井中的甲烷浓度等,具有实用价值.
2 传统WMS 技术及甲烷测量实验
2.1 传统WMS 技术理论
顾名思义,波长调制光谱技术需要对半导体激光器出射激光的波长进行调制.设半导体激光器注入电流是一个以ω为角频率的余弦信号 c os(ωt),那么激光的光强和光频分别可以表示为[28]

其中I0表示归一化的平均光强;i1和i2分别为光强的线性调制幅度与二次谐波调制幅度;ψ和δ分别表示线性调制相位和二次谐波调制相位;ν为激光的中心频率;a为频率调制幅度;φ为光的频率、光强相位差.实际上,i1通常比i2大一个数量级,所以通常认为i2=0 .
气体对光的吸收行为可用朗伯比尔定律描述:

其中It和I0分别为透射光强与入射光强;α(ν) 为气体的吸收系数;C和L分别为气体的浓度(本文中的浓度均指体积分数)和光在气体中通过的距离.根据泰勒级数展开,

当x≪1 时,可用一阶近似1 —x替代 e−x,近似误差(err)的典型值为:x=0.05 时,err=0.13%;x=0.1 时,err=0.53%;x=0.2 时,err=2.29%.可以看到,随着x的增大,1 —x的近似误差急剧增加;若要求该一阶近似的准确度不低于99.5%,则要求x<0.1.结合(3)式可知,当气体的吸收度α(ν)CL ≪1时,朗伯比尔定律可以近似为

(5)式称为朗伯比尔定律的“弱吸收近似”.
把(1)式与(2)式带入(5)式中可得

根据(6)式与(7)式可知,如果用正交的参考信号对It(t) 进行锁相放大,分别得到二次谐波(2f)信号的X分量与Y分量,它们分别可以表示为
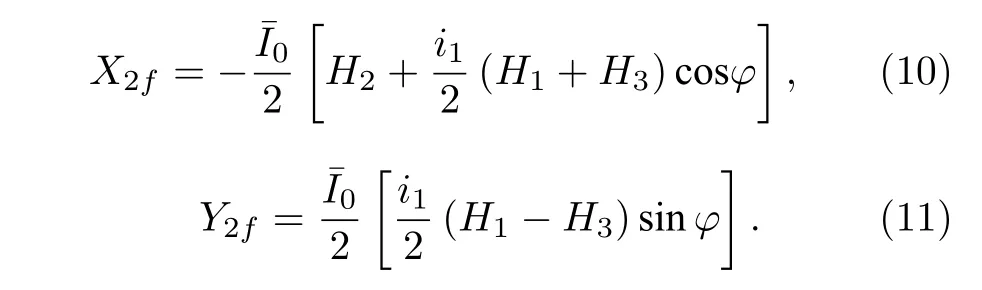
对于理想的吸收线型而言,在中心频率ν0处有:H1(ν0)=H3(ν0)=0,则可以得到,中心频率ν0处的二次谐波幅值为

再结合(9)式可知,二次谐波信号在中心频率处的值与气体的积分浓度CL成线性关系.然而,该线性关系建立在朗伯比尔定律的一阶近似即(5)式之上.如果气体的吸收度较大,该弱吸收近似就不再成立,便会导致R2f(ν0) 与积分浓度CL之间的线性关系不再成立.
2.2 利用传统WMS 技术测量甲烷气体
实验中测量的甲烷吸收峰位于1653.7 nm 附近,如图1 所示.
实验中使用的光源为NEL 公司生产的分布式反馈激光器(DFB),输出激光的波长范围可以通过温度与电流进行调谐,能够输出1625—1655 nm近红外光,可以覆盖图1 所示的甲烷吸收峰.实验装置如图2 所示: 信号发生器产生50 Hz 锯齿波与5 kHz 正弦波的叠加波形,输入激光控制器;激光控制器可以通过PID 闭环控制,使激光器处于稳定的工作温度,并可以将信号发生器产生的电压信号转换为电流信号,加载给DFB 激光器;DFB激光器的输出激光经过准直后进入总光程为8 m的怀特型多光程气体吸收池,在气体池的光出口处使用铟镓砷红外光电探测器接收出射光;探测器的响应经过数据采集卡的模数转换,交由卡片式计算机树莓派4B 处理,可以实现数字锁相放大、信号提取等后续数据处理操作.

图1 1653 nm 附近处的甲烷吸收线型(P =1 × 105 Pa,T =296 K)Fig.1.Absorption profile of methane around 1653 nm (P=1 × 105 Pa,T=296 K).
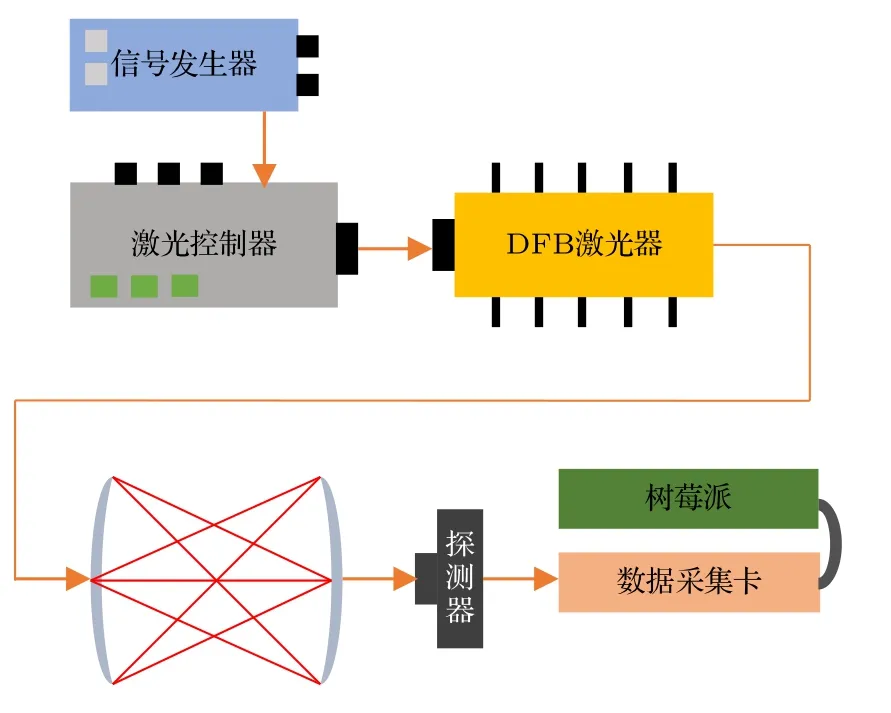
图2 基于WMS 技术测量甲烷气体的实验装置示意图Fig.2.Illustration of the WMS−based methane measuring system.
为了说明传统WMS 技术在测量高吸收度气体时的局限性,实验测量了体积比为100.9×10—6,500.9×10—6,1002×10—6,2996×10—6,6960×10—6和10510×10—6的甲烷,根据图1 可知,对应的甲烷吸收度范围在0.024—1.78 之间.实验中典型的二次谐波波形如图3 所示,其峰值即为(12)式中的R2f(ν0).
通过测量上述6 个浓度下的二次谐波值,可以得到如图4 所示的二次谐波幅值与甲烷浓度之间的关系.可见,当甲烷的吸收度较大时,朗伯比尔定律的弱吸收近似不再成立,便会导致(12)式中所描述的二次谐波与气体积分浓度之间的线性关系不再成立.这是WMS 技术的局限性所在,即其仅适用于弱吸收情形,下一小节将详细介绍针对此局限性的改进方法.
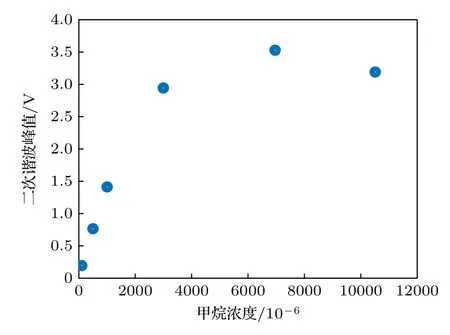
图4 WMS 实验中甲烷的二次谐波幅值与甲烷浓度之间的关系Fig.4.Relationship between the amplitude of the 2nd har−monic of methane and the concentration of methane in the WMS experiment.
3 改进的WMS 技术及甲烷测量实验
3.1 改进的WMS 技术理论
根据上一小节的分析可知,WMS 技术之所以只能保证弱吸收下的线性响应,是因为其理论建立在朗伯比尔定律的弱吸收近似上,所以如果要使得WMS 能够适用于任意高的吸收度,就要基于朗伯比尔定律的原型推导WMS 理论.弱吸收近似的本质是使用线性表达式取代e 指数项,自然地想到,对朗伯比尔定律两边同时取自然对数也可以达到类似的效果.对(5)式式两边同时取自然对数并结合(1)式可得

根据泰勒级数公式:

可以把(13)式.等号右边的第二项写作:

(15)式中的第二个等号变换的依据是三角函数的积化和差变换,其中n为i1的多项式,是与激光参数有关的常数.
根据(7)式的傅里叶级数展开以及(15)式,对(13)式进行改写:
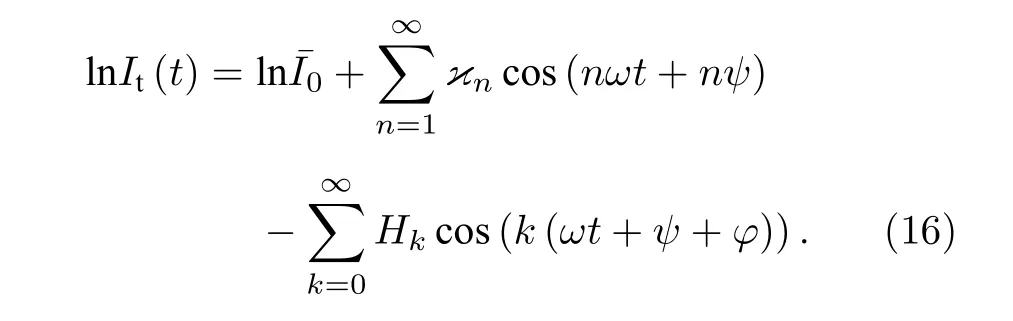
气体的吸收效应在(16)式等号右侧的第三项,如果没有气体吸收,即激光器输出的激光直接被探测器接收,光强可表示为

如果使用 c os(ωt+ξ) 作为参考信号对lnIt(t)NA锁相解调,得到的一次谐波的表达式为

在确定了ξ之后,使用 c os(2ωt+2ξ) 作为参考信号对 l nIt(t) 锁相解调,可以得到气体吸收信号的二次谐波:

3.2 利用改进的WMS 技术测量甲烷气体
通过前面理论分析可知,改进的WMS 需要有一个参考通道,目的是为了得到未经气体吸收的光强信号It(t)NA.实验装置如图5 所示,激光被分为90:10 两路,90%的一路进入气体池,经过甲烷气体的吸收后被探测器接收;10%的一路直接被探测器接收.两个探测器的响应分别输入到数据采集卡的两通道中,经过模数转换后由树莓派进行数据处理.参考通道和测量通道的波形示意图分别如图6及图7 所示.

图5 基于改进的WMS 技术测量甲烷气体的实验装置示意图Fig.5.Illustration of the modified−WMS−based methane measuring system.
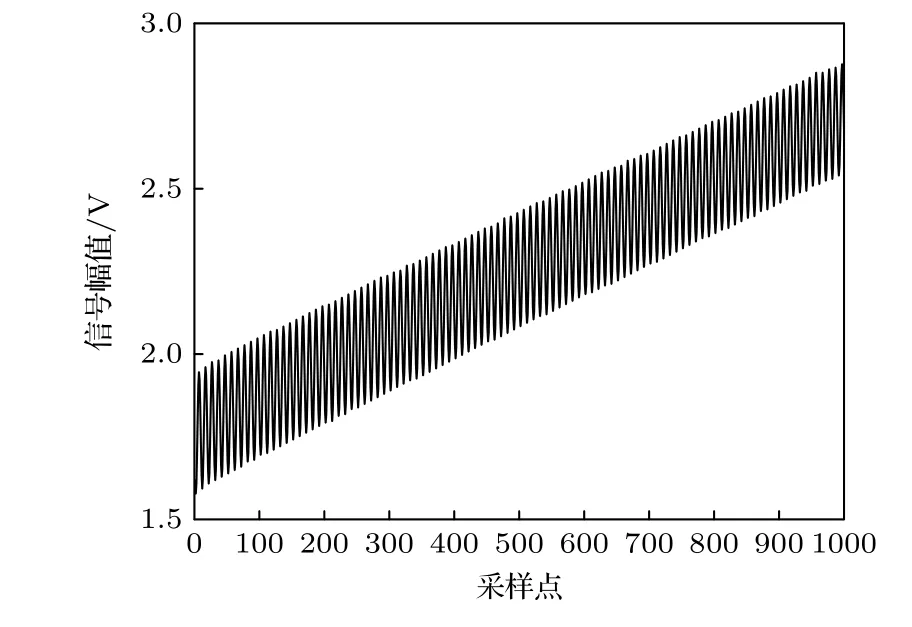
图6 参考通道波形示意图Fig.6.Illustration of the waveform of the reference channel.

图7 测量通道波形示意图Fig.7.Illustration of the waveform of the measurment channel.
在实验中同样使用体积比为100.9×10—6,500.9×10—6,1002×10—6,2996×10—6,6960×10—6和10510×10—6的甲烷气体,吸收度在0.024—1.78 区间.先利用参考通道确定二次谐波的解调相位,再对测量通道的信号进行锁相解调,得到二次谐波信号,如图8 所示.

图8 改进的WMS 实验中甲烷的二次谐波信号示例Fig.8.Illustration of the 2nd harmonic of methane in the modified−WMS experiment.
可见,与传统WMS 相比,改进后的WMS 的二次谐波信号可能出现负值,这是因为传统WMS的正交锁相放大有平方和的操作((12)式),而改进的WMS 中没有类似操作.
为了验证在高吸收度下,改进的WMS 中二次谐波响应也可以与甲烷浓度之间保持线性关系,分别测量了在上述6 个甲烷浓度下二次谐波的幅值,它们的关系如图9 所示.可见,即使在高吸收度下,基于改进的WMS 理论的二次谐波测量结果也能保持与甲烷浓度之间的线性关系,对测量点进行线性拟合,可以得到拟合方程为:y=−9.0507×10−5x−0.0076,拟合优度为0.9984.由此可以验证,改进的WMS 技术相比于传统的WMS 有更大的线性范围,适用于气体浓度变化范围很大的应用场景,比如实时监测地下矿井的瓦斯气体浓度等.

图9 改进的WMS 实验中甲烷的二次谐波幅值与浓度的关系Fig.9.Relationship between the amplitude of the 2nd har−monic of methane and the concentration of methane in the modified−WMS experiment.
4 结果分析与讨论
4.1 改进的WMS 技术的二次谐波解调相位
通过第3 小节的介绍可知,在改进的WMS 技术中,二次谐波信号的解调需要明确的解调相位2ξ,而不是像传统WMS 那样,使用两个正交的参考信号解调得到二次谐波.二次谐波的解调相位是依据未被吸收的光信号实时得到的,通过优化算法使得It(t)NA的一次谐波绝对值最小化,对应的一次谐波解调相位ξ即为所求.ξ的取值与多方因素有关,比如信号发生器所产生的调制信号的相位、激光控制器内部电路引入的信号相移等,它们虽可以视为实验仪器的本征参数,但并不恒定,导致解算出来的ξ并非固定值,而是在一定区间内都有分布.图10 给出了在1000 次连续测量中解算出来的ξ值的频率分布直方图,显然ξ并不固定,而是呈现近似的均匀分布.这说明实时解算ξ是有必要的,并不能事先确定ξ的数值.

图10 1000 次连续测量中解算出的 ξ 值的频率分布直方图Fig.10.Frequency histogram of the value of ξ calculated in 1000 continuous measurements.
4.2 基于改进的WMS 技术的甲烷测量系统的噪声水平评估
由于噪声的影响,实际测量系统的测量值会呈现一定程度的波动,而通过多次测量取平均则可以降低噪声的干扰,使得测量数据的稳定性得到提升.艾伦标准差通常用以评价一个测量系统的噪声水平,其反应了在一定的平均时间下,测量数据的波动情况.假设一个系统的测量时间间隔为τ,n次连续测量结果为y1,y2,···,yn,如果每m(m<n)个测量结果取平均,得到序列Y1,Y2,···,YN,其中此时对应的平均时间为mτ.则在平均时间mτ下,艾伦标准差的表达式为[29]
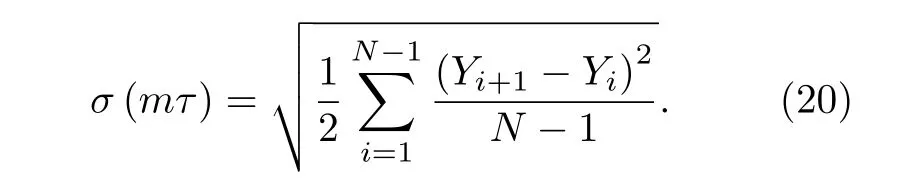
该甲烷测量系统的艾伦标准差分析如图11 所示,可以得出,该测量系统在平均时间为103.6 s时艾伦标准差达到最低,体积比为26.62 × 10—9.

图11 基于改进的WMS 的甲烷测量系统的艾伦标准差分析Fig.11.Allan deviation analysis of the modified−WMS−based methane measurement system.
5 结 论
本文使用改进的WMS 技术对强吸收的甲烷气体进行了测量,相比于传统WMS,该改进技术可以保证在高吸收度下,甲烷吸收的二次谐波幅值与浓度之间的线性关系仍然成立,其中最本质的原因在于,传统WMS 理论建立在朗伯比尔定律的一阶近似之上,而改进的WMS 是以朗伯比尔定律的原始形式为基础推导而得.传统WMS 中一阶近似的核心作用是使得气体吸收项αCL从非线性项(e 的指数)变为线性项,从而使得最终的二次谐波表达式也是一个关于CL的线性表达式;而改进的WMS 则是通过对朗伯比尔定律的原型取对数的方式,使得原本在e 的指数部分的吸收项αCL成为线性项,起到了与一阶近似类似的作用.取对数的好处是,这是一个严格的数学变换,不会引入任何近似误差.通过对6 个不同浓度的甲烷进行实验测量,验证了传统WMS 在甲烷吸收度比较高时已经失去了线性响应,而改进的WMS 则可以始终保持线性响应.这种改进方法极大地拓展了传统WMS 的适用范围,打破了其内在的低吸收度限制,为扩大甲烷气体测量的应用场合奠定了基础.

