二维气体模型中的负微分热阻*

黄礼胜 罗荣祥

(福州大学物理系,福州 350108)

负微分热阻效应是指在一个热输运系统中增大热流驱动力热流反倒减小的现象.理解和控制非平衡热输运系统中的负微分热阻效应,并利用其设计制造新功能热器件是科学技术的前沿挑战,有着重要的理论意义和应用前景.相对晶格模型中的负微分热阻研究而言,流体模型中的负微分热阻性质还亟待认知.本文选用由多粒子碰撞动力学描述的二维气体模型为研究对象,理论证明了热库对气体粒子运动的约束是诱导负微分热阻的一个新机制,并通过非平衡分子动力学方法揭示了该机制仅适用于弱相互作用的小尺寸系统.这些结果为气体模型能表现出负微分热阻现象提供了微观机制的支持,同时也为开发新的应用提供了新思路.

1 引 言

考虑到日益增长的能源需求以及化石燃料对生态环境的影响,人们一直致力于开发新能源和提高能源的利用效率.在这个背景下,新功能热器件的开发对解决或缓解能源危机具有重要的意义.实现新功能热器件的关键点在于全面深入地理解各种热输运现象[1−5],如热传导、热电效应、热整流、负微分热阻、热隐身等.目前,这些热输运现象的研究已经取得了一系列重要的成果,极大地促进了非平衡态统计物理理论与实验在各个方向的发展,由此形成了与上述现象密切相关的热输运理论和实验研究为中心的热点[2,4−7].本文主要对负微分热阻展开相关的研究.

随着人们对低维热输运的探索日益加深,负微分热阻的理论研究在近20 年得到了快速发展.2004 年Li 等[8]在研究非对称的Frenkel-Kontorova晶格模型热整流时注意到了负微分热阻效应.两年后,基于对负微分热阻的认识,他们的研究工作为设计制造热三极管提供了理论依据[9].在控制热流已经成为可能的情况下[10],这些开创性的工作在设计新功能热器件领域启发了许多后续工作.迄今的理论研究表明,负微分热阻在设计热三极管、热逻辑门、热存储器以及热流限制器中起着关键性的作用[9,11−13].研究晶格模型中的负微分热阻能为设计制造新功能固体热器件提供直接的理论指导依据,因此在过去的十多年里,人们对晶格模型进行了大量的理论和数值研究.到目前为止,人们已经在各种具有不同非线性相互作用的晶格模型中观测到了负微分热阻现象[9,14−19],也揭示了系统各种参数对负微分热阻性质的影响[20−24].对于负微分热阻的微观起源,人们的研究表明晶格模型中的负微分热阻现象可以从声子相互作用[9]和声子模的动力学局域化[25]的角度去理解,而且还给出了晶格模型要产生负微分热阻现象需要满足的一些必要条件[24,26].尽管负微分热阻的研究在实验上尚未取得突破性进展,但显然,晶格模型中的负微分热阻的理论研究已经取得了显著的成绩.

近来的研究表明,负微分热阻仍有许多未被人们充分认识以及尚未被发现的新现象和新机制.除了在晶格模型和宏观经典系统中取得的最新进展[27,28],更令人吃惊的是,2019 年的研究发现,代表流体类的一维气体模型在可积和不可积的情况下热库对气体粒子运动的约束是诱导负微分热阻的一个新机制[29].值得注意的是,可积的晶格模型中是不存在负微分热阻现象的.也就是说,这一工作不仅证明了流体模型也存在负微分热阻现象,而且还证实了两种模型之间的负微分热阻性质存在本质上的区别.众所周知,流体模型中的热载流子(分子、原子、离子)在相互作用力和调控方法上与晶格模型中的声子存在本质上的区别.因此,从新的流体模型视角出发对负微分热阻展开研究,势必有助于揭示负微分热阻的新现象和新性质,甚至有可能会导致理论和实验上的新突破.

负微分热阻效应具有哪些特征以及这些特征产生的条件和机制是一个重要的基本物理问题.然而,选用流体类模型来研究负微分热阻的工作还未深入展开.虽然在流体类模型负微分热阻研究的第一篇工作中证明了热库对气体粒子运动的约束是诱导负微分热阻的一个新机制,也揭示了该模型负微分热阻与系统参数之间的重要性质[29].但是,作为说明例子,该机制目前仅在一维弹性碰撞相互作用的原子气体模型中得到了数值验证,揭示的负微分热阻性质也仅是该模型在特定参数下的情况.众所周知,粒子与热库的相互作用是不受空间维度限制的,粒子间的相互作用也不仅局限于弹性碰撞.因此,目前急需回答的一个重要的基本问题是,热库诱导的负微分热阻机制是否也适用于更具有一般性的高维流体模型? 若适用,值得进一步研究的问题是高维流体模型的负微分热阻效应将具有哪些新性质? 搞清楚这些对理解特定条件下流体系统的负微分热阻性质和开发其新应用都有极大的帮助.

为对上述问题给出明确的答案,本文选用更具有一般性的二维气体模型来阐明其在特定条件下的负微分热阻性质.要从微观角度搞清楚二维气体模型中的宏观输运性质,关键的一个技术是要化简气体粒子间的相互作用使得其动力学演化能够被分子动力学模拟,同时要求这种简化能够正确地保留流体力学方程的性质.符合这一要求且已成功应用的关键数值技术被称为“多粒子碰撞方法”[30],目前该方法还被成功应用于带电多粒子系统的非平衡热输运研究[31,32].本文将利用该方法数值证明热库对粒子运动的约束也是诱导二维气体系统出现负微分热阻效应的机制,并进一步揭示该机制仅适用于弱相互作用的小尺寸系统的性质.这些结果将会深化人们对流体模型负微分热阻基本原理、性质及其应用相关的重要问题的认识.

2 二维气体模型

本文研究的二维气体模型如图1 所示.N个质量为m的粒子被限制在长度为L、宽度为W的长方形系统中.为驱动系统形成稳定的热流,把两个统计力学热库与系统的两端相耦合,其中TL和TR是系统左端和右端的热库温度.当粒子与热库发生碰撞时,将从热库的速度分布函数中随机选择一个速度作为粒子的新速度反射回系统中.满足热库的速度分布函数为[33,34]

图1 由多粒子碰撞动力学描述的与热库耦合的二维气体模型示意图Fig.1.Schematic drawing of the two-dimensional gas model described by the multi-particle collision dynamics.The system is coupled at its left- and right-hand ends to two thermal baths of fixed temperature T L and T R .The x coordinate goes along the channel and y is perpendicular to it.

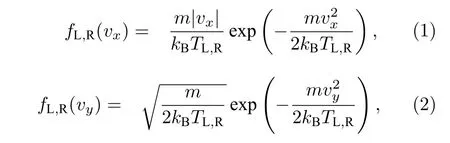
其中vx和vy是粒子在横轴和纵轴方向的速度,kB是玻尔兹曼常数.在数值模拟中,vx ＞0 (vx ＜0)表示从左端(右端)热库选择粒子速度.需要强调的是,不管在y轴方向取周期性边界条件还是固定边界条件,由于两种情况下粒子的速度vy ＞0 和vy ＜0都是等概率的,因此所得的结果不依赖于边界条件.

图1 所示系统的动力学演化可用多粒子碰撞方法来模拟.多粒子碰撞方法在物理学研究中之所以能够被广泛应用,是基于其可以正确地保留流体力学方程的性质,还可以化简动力学演化的数值模拟[30].简单地说,该方法通过对时间和空间的粗粒化使得系统的动力学演化过程分为两步.第一步,粒子在时间步长为τ的时间间隔内在系统中自由运动,其位移随时间t的演化方程为

其中ri和vi表示系统中第i个粒子的位移和速度.第二步,每演化一个步长,系统中的粒子速度将更新一次,用来模拟粒子间的相互碰撞.首先,把系统均匀地分成许多个小单元格(如图1 虚线所示),每个单元格的边长为a.然后,把每个单元格中的粒子速度都绕其质心速度做一个旋转操作,旋转角θ可以是任意角度.在二维系统中,旋转方向可以是顺时针(+θ)、也可以是逆时针(−θ),两者的取值概率相同.因此,粒子在每个单元格中的速度演化方式可以表示为

需要强调的是,粒子的速度由于旋转操作将发生改变,但旋转操作并不改变每个单元格中粒子的总能量和总动量.基于旋转操作的这一特点,多粒子碰撞方法已被成功应用于研究动量守恒系统的热传导行为[31,35,36].在数值模拟中,通过调整步长τ的取值,可以调控粒子间的相互作用强度,进而也会影响系统的输运性质.

在数值模拟中,令系统左右热库温度分别为TL=1 和TR=1−ΔT,其中 ΔT为系统两端温差.同时,其他的主要系统参数被设置为m=kB=W=1,a=0.1 ,θ=π/2 ,系统的粒子数密度为ρ=N/(WL)=22.系统演化的初始条件为随机给定每个粒子的位置和速度.当系统经过长时间演化达到非平衡稳态后,再根据定义计算系统的热流,其中热流的定义为单位时间单位面积内粒子与热库交换的能量.在数值模拟中,我们在y轴方向取的是周期性边界条件,且已数值检验了本文所得的数据与系统宽度无关.

3 理论分析

接下来给出图1 所示系统在可积条件下的热流表达式,并揭示热库诱导该系统出现负微分热阻的机制.在可积的条件下,即在不考虑系统粒子相互作用的情形下,可解析得到流过系统的热流,推导过程如下.若系统中只有一个粒子,当该粒子与左（右）边界碰撞时,粒子反射回系统的平均动能EL(ER)可表示为

因此,该粒子在热库之间传递的平均动能为

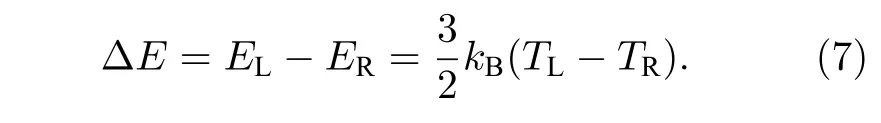
该粒子从左端热库运动到右端热库所需要的平均时间tL→R可以表示为

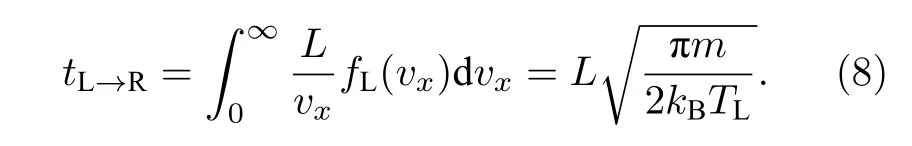
同理,可以得到tR→L.因此该粒子在两热库之间传递一次能量所需要的平均时间为

根据热流的定义,可知当系统仅有一个粒子时,其热流为

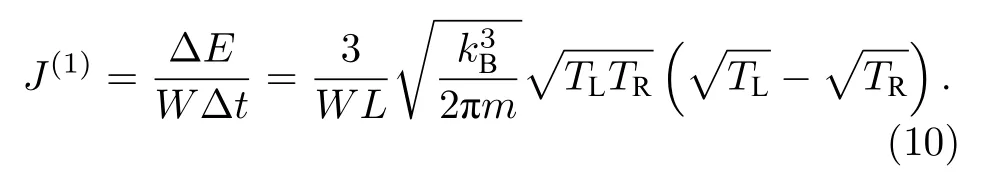
对于N个无相互作用的多粒子系统,其热流是J(1)的N倍,即为

其中,ρ=N/(WL) 是系统的粒子数密度.

若热库温 度设置为TL=1 和TR=1−ΔT,ΔT ∈[0,1).(11)式可以表示为

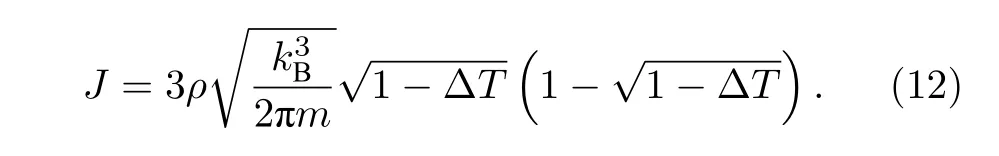
根据(12)式可画出系统热流J与温差 ΔT的函数关系,结果如图2 红色实线所示.可以看出,当ΔT ＞0.75 时,J随ΔT的增大而减小,系统表现出了负微分热阻现象.值得强调的是,由(12)式可知,在可积情况下负微分热阻的存在并不依赖于系统的粒子数密度、系统温度和粒子质量.

图2 不同时间间隔 τ 下,热流 J 与温差Δ T 的函数关系.红色曲线为(12)式给出的解析结果,符号数据点是系统尺寸 L =64 时的数值结果.黑色点虚线是出现负微分热阻现象的参考线Fig.2.The heat current J as a function of temperature difference Δ T for various time interval τ .The red curve is the analytical result given by Eq.(12).The symbols are for the numerical results and obtained for L =64,and the black dashed line is drawn for reference.

(13)式表明,f随 ΔT的增大而减小,意味着降低低温热库的温度(TR=1−ΔT)将减小粒子与高温热库的碰撞次数,进而使单位时间内热库之间交换的热量也随之减小.可知,通过降低热库温度来增大 ΔT,虽然可使粒子在热库之间单次传递的平均热量增加,但由于f的减小也将使系统的热量交换受到抑制.因此,ΔT和f对热流均有贡献、且为竞争关系: 当减小f对热量交换的抑制效应大于ΔT对热量交换的促进效应时,系统将产生负微分热阻效应.为了更好地理解这个性质,可以分析一个极端情况来阐明其物理图像,即在TR→0 的情况下,由于粒子与低温库碰撞后反射回系统的速度趋于零,使得该粒子停在低温热库端.这个极端现象可以简单地理解为粒子被低温热库冻住了,进而导致热库之间的热流将如图2 红色实线所示趋于零值.基于上述微观动力学分析,得到的结论是降低热库温度能诱导二维气体模型产生负微分热阻效应.

4 数值结果

为了验证上述理论分析结果,通过分子动力学方法数值测量了可积情况下不同温差时的热流值,测量结果如图2 中的黑色数据点所示.从图2可以清楚地看到,可积情况下我们的数值结果与理论分析结果((12)式)完全一致.这一结果为上述理论分析提供了强有力的证据,证明热库的确能诱导二维气体模型产生负微分热阻效应.

众所周知,由于可积系统的热输运是弹道的、热库之间并不存在温度梯度,所以可积情况是非常特殊、平庸的结果.因此,现在最重要的是要确认热库诱导的负微分热阻机制是否也适用于更一般的考虑粒子相互作用时的不可积情况.若适用,进一步要搞清楚的是该机制的适用范围.为了搞清楚这些问题,本文继续用分子动力学方法研究不同粒子相互作用强度和不同系统尺寸对该诱导机制的影响.

如前所述,通过取不同步长τ值可调控粒子间的相互作用强度,因此数值给出不同τ值下热流与温差的函数关系便可知不同粒子相互作用强度对该诱导机制的影响.图2 给出了系统尺寸L=64时,不同τ值下J与 ΔT的关系.注 意τ→∞时 对应可积情况下的数值结果,所以τ越小表示粒子间相互作用越强.从图2 可知,考虑相互作用后的不可积系统也存在负微分热阻,但随着τ的减小负微分热阻的存在区间将逐渐减小直至消失,即粒子间的相互作用越弱负微分热阻效应越明显.由这些数值结果可知,通过降低热库温度来产生负微分热阻效应的机制仅适用于弱相互作用的模型系统.

接下来研究当粒子间的相互作用强度不变时,不同系统尺寸对该诱导机制的影响.图3 给出了粒子相互作用强度τ=1.0 时,不同L下J与 ΔT的关系.从图3 可知,负微分热阻的存在区间随系统尺寸的增大而减小,并最终消失.这一数值结果表明降低热库温度仅能诱导小尺寸的系统产生负微分热阻效应.结合图2 和图3 的数值结果,最终可得到的结论是热库诱导的负微分热阻产生机制仅适用于具有弱相互作用的小尺寸系统.这个结论可能对理解和控制微纳米尺度下的流体热输运有一定的帮助[37−39].

图3 不同系统尺寸L 下,热流 J 与温差 Δ T 的函数关系.这里时间间隔τ=1.0Fig.3.The heat current J as a function of temperature difference Δ T for various system size L. Here we set τ=1.0.

最后解释强相互作用和增大系统尺寸导致负微分热阻效应消失的原因.控制系统行为的关键参数是粒子在穿过系统时与其他粒子相互碰撞的“机会”数量,或称之为碰撞概率.根据多粒子碰撞方法的数值特点可知,这个参数与τ的关系为负相关、与L的关系为正相关,即减小τ值和增大L都将增大粒子间的碰撞概率.由于碰撞越频繁粒子间的动量交换越充分,使得从低温热库反射回系统的慢速粒子的速度得以提升.因此,粒子间的碰撞概率越大,将越显著地削弱低温热库对反射粒子运动的约束,最终导致热库诱导的负微分热阻效应在强相互作用和大系统尺寸的情况下失效.

5 结论与讨论

本文研究了由多粒子碰撞动力学描述的二维气体模型,解析给出了可积情况下该系统的热流表达式,揭示了热库能诱导负微分热阻效应的物理机制.从动力学的角度说,这个机制是通过不断降低低温热库的温度来约束粒子的运动,使得粒子与高温热库的碰撞率越来越小,进而导致高低温热库间的热量传递受阻.此外,本文通过分子动力学方法研究了二维气体模型中系统粒子间相互作用强度和系统尺寸长度对该负微分热阻诱导机制的影响,研究发现: 1) 负微分热阻的存在区间随着系统粒子间相互作用强度的增大而逐渐减小直至消失;2)负微分热阻的存在区间随系统尺寸长度的增大而逐渐减小直至消失.综上,本研究得到一个具有普适性的结论,即对于弱相互作用的小尺寸气体热输运系统,减小低温热库温度能诱导该系统产生负微分热阻效应.

本文涉及的主要是关于系统界面与外界热库相互作用的理论结果,与前人研究界面对热传导和热整流的影响一样[40−42],这些研究结果共同说明在特定条件下,界面与热输运系统的相互作用将会产生新颖的物理效应.我们注意到多粒子碰撞动力学模拟方法已被成功应用于等离子体系统的热输运研究[31],因此本文揭示的热库诱导的负微分热阻机制可能也适用于弱耦合的小尺寸等离子体系统.我们还注意到在具有弱相互作用的超冷原子中已经观测到了热电转换效应[43],因此在冷原子环境中可能也能够观测到负微分热阻效应.此外,与晶格模型中的负微分热阻研究类似[9,11−13],我们期待本文揭示的负微分热阻机制能被用于设计制造流体热三极管及其他更加复杂的流体类新功能热器件.最后,值得指出的是,本研究所选用的气体模型是介观物理研究中非常受欢迎的模型[30],因此我们推测本文揭示的机制可以在介观系统中得到实验验证,并在不远的将来找到有趣的应用.