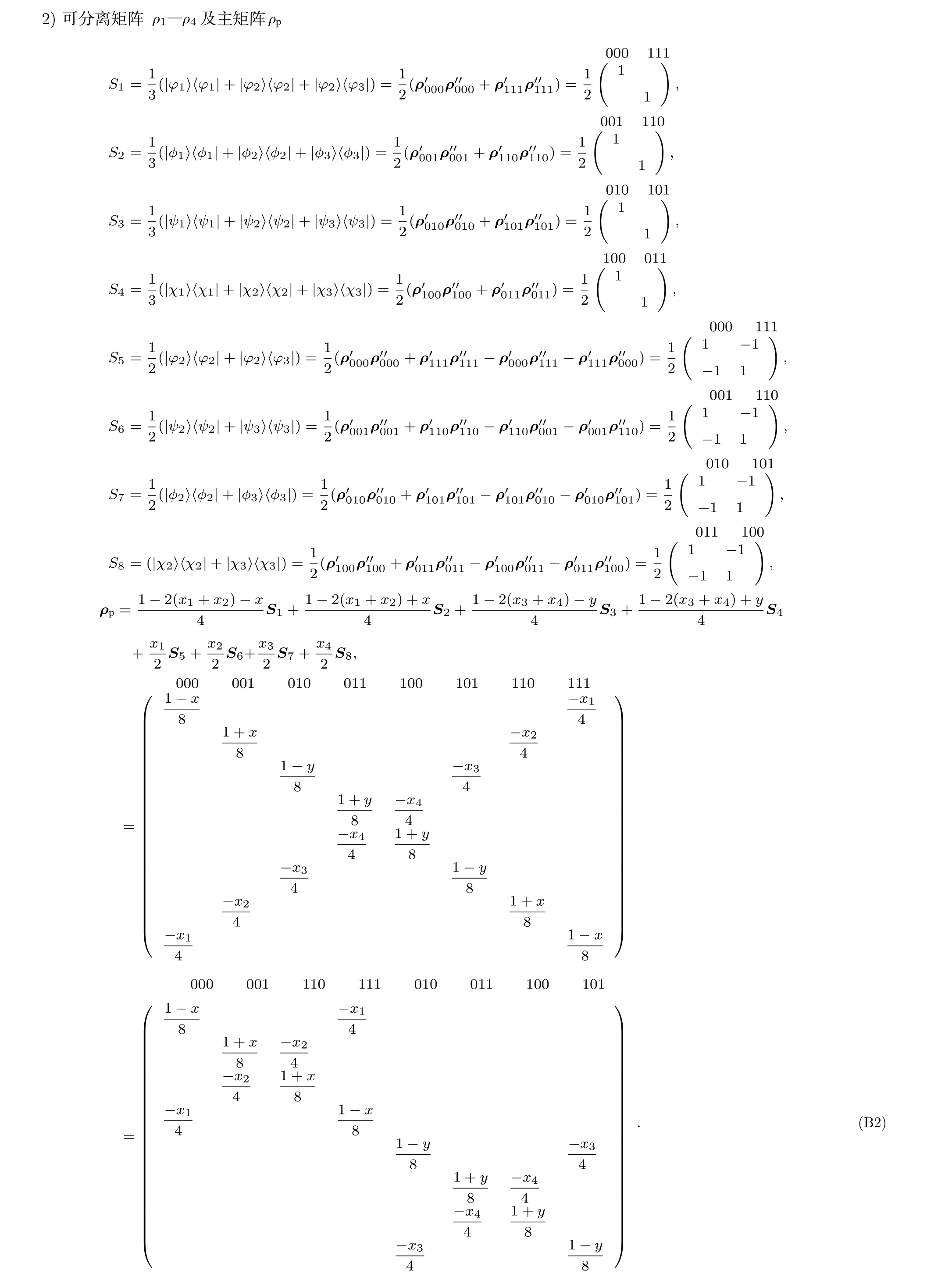
N 量子比特系统的纠缠判据*

谭维翰 赵超樱 郭奇志

1) (上海大学物理系,上海 200444)

2) (杭州电子科技大学物理系,杭州 310018)

3) (山西大学光电研究所,量子光学与光量子器件国家重点实验室,太原 030006)

在前文(2019 Int.J.Mod.Phys.B 33 1 950197;2020 Int.J.Mod.Phys.B 34 2050022)中,我们提出了一种判断2 量子比特系统纠缠的方法,2 量子比特系统可分的充分必要条件是相关系数为正且主密度矩阵可分,否则系统纠缠.在本文中,通过数值计算与讨论,先将2 量子比特系统纠缠判据的方法推广到3 量子比特系统中去;接着,继续将3 量子比特系统推广到N 量子比特系统中去.这是一个复杂而有趣的问题.

1 引 言

自从上世纪三十年代Schrödinger 提出量子纠缠态的概念以来,有关量子纠缠态的研究就从未间断过.量子纠缠态在量子密钥分配、量子密集编码、量子隐形传态、量子纠错码和量子计算等诸多领域有着重要的应用.但是,迄今为止,仍有许多理论问题没有得到解决,这些都制约着实验工作的进展.量子纠缠理论的发展将为量子信息技术打开广阔的应用前景,其研究是当前国际上量子信息论和量子光学等学科关注的前沿课题之一.

近年来,纠缠态在量子计算、量子纠错等方面具有很大的应用前景[1−3],但是关于纠缠本质等的基本问题还没有解决,一个非常引人注目的量子现象是复合量子系统的纠缠[4−6].Peres 的PPT 判据和Horodecki 的约化判据.Peres 和Horodecki 等最早提出经PPT 后系统特征值是否全为正来判别该系统为可分或纠缠.Peres 判据,从物理本质上来看就是对两体中的任一单体做部分时间反演操作.对于2×2 维和2×3 维系统,它是充要条件;对于其他情况,它是必要非充分条件.Horodecki 等采用约化判据对2×4 维和3×3 维系统做了详细的研究.最近又有关于 2×N维和N×N维系统的研究报道,计算相当繁琐.Werner[7]基于对局部隐变量模型的分析和翻转算子均值的正定性给出了一个判据.Horodecki 等[8,9]得到了一个关于所谓熵的不等式形式的判据.Peres[10]判据基于部分转置后密度算符的正定性.由两个子系统组成的量子系统是可分的,当且仅当密度矩阵可以写成两个子系统的密度矩阵,其中,权重满足为正条件时,系统是可分的,否则系统是纠缠的.Peres-Horodecki 准则是充要条件[11−16].

由于非对角矩阵元的存在,求密度矩阵ρ的解析解比获得ρ可分的充要条件要困难得多.这是一个更为复杂和有趣的基础物理问题.2019 年,我们课题组采用标准矩阵法研究了任意2×2 复合系统密度矩阵ρ的解析解.该解可以表示成主密度矩阵和可分离密度矩阵ρ1—ρ4的和,如果这些几率是全正的,则密度矩阵ρ可分,并且分离后的密度矩阵也一并求出来了.如果这些几率不是全正的,则复合系统就是纠缠的.可以很容易就验证出几个已知2×2 系统的不可分判据与PPT 判据一致[17].2020 年,我们研究任意3×3 复合系统密度矩阵ρ的解析解.将密度矩阵ρ分解为主密度矩阵ρp和六个约化密度矩阵ρ1—ρ6的总和,给出判断两个三量子态(0,1,2)系统纠缠的充要条件,并得出几率是全正的解[18].在这篇文章中,只讨论二量子态(0,1),即通常说的量子比特.我们试图将前文[17]用方法推广到N量子比特系统.第一步是3 量子比特系统;第二步到N量子比特系统.本文的安排是:第2 节对2 量子比特系统纠缠判据的简介.第3 节将上述解决方案推广到N量子比特系统.第4 节是关于2 量子比特和3 量子比特系统的数值计算.

2 量子比特系统纠缠态解析解简介

对于一个单量子比特系统,上能级 |1〉,下能级|0〉 .2 量子比特的基向量 |00〉,|01〉,|10〉,|11〉 是所有纠缠态的基.一般的,假设密度矩阵元素是实数,2 量子比特系统的密度矩阵ρII具有如下的形式:

3 N 量子比特系统纠缠判据

3.1 3 量子比特系统纠缠判据

应用上方法研究了3 量子比特的纠缠态问题.这个方法包括写出基函数,由此构成的可分离的密度矩阵,进一步便是3 量子系统主矩阵(详细见附录B).先按附录A 导出(2)式的办法导出下面3 量子系统的相应方程(3).这过程很复杂,很难被推广到N量子比特系统.但有趣且有用的是我们发现3 量子系统主矩阵可表示为2 量子系统的对角矩阵(见附录(B2)式).这就为下面推广到N量子比特系统成为可能:

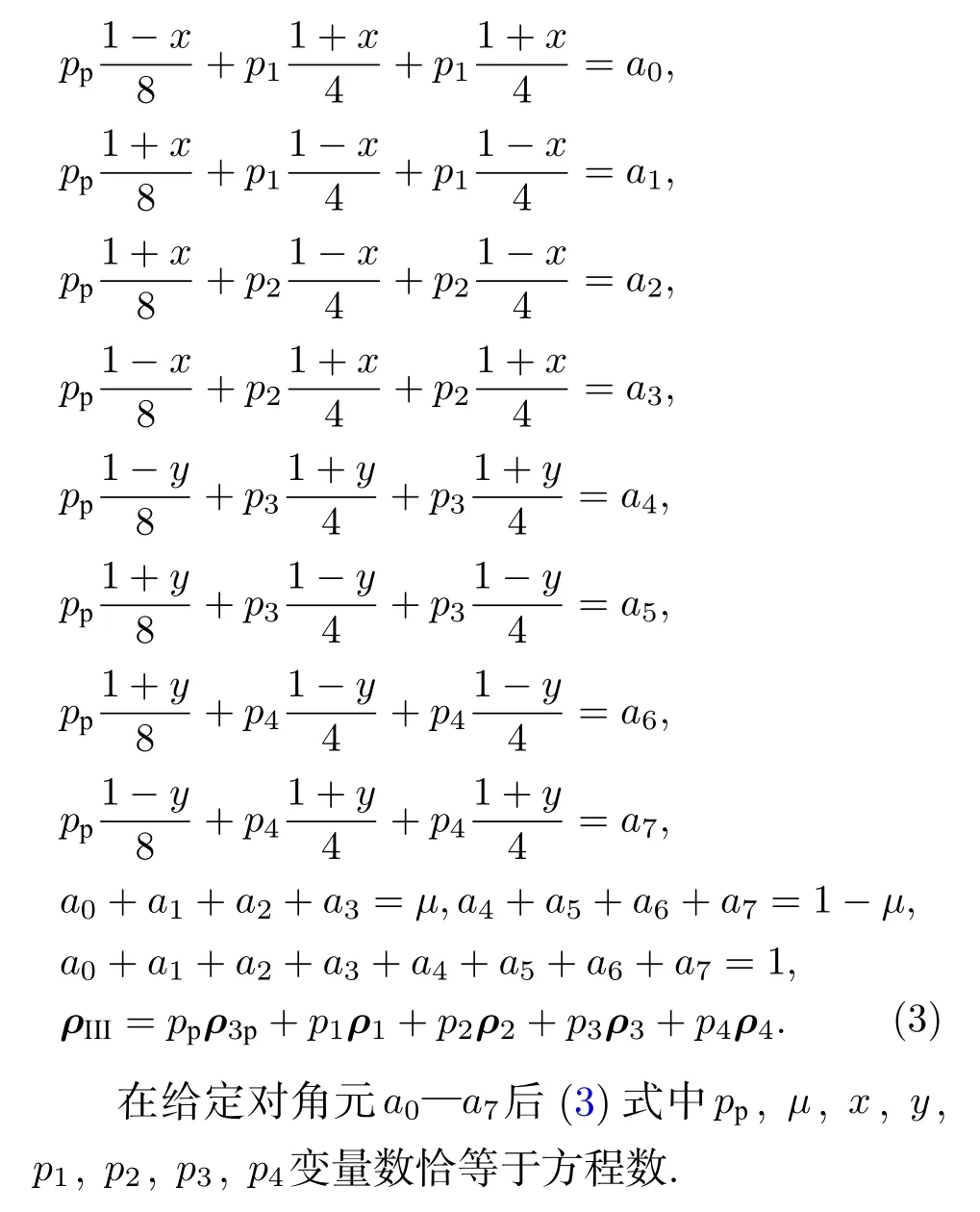
3.2 N 量子比特系统纠缠判据

一般来说,N量子比特系统的密度矩阵可以由矩阵ρn=AN表示出来,其秩为N=2n.对于3 量子比特系统,矩阵的秩为N=23=8 .假设密度矩阵元素是实数,3 量子比特系统有如下形式[19]:

其中

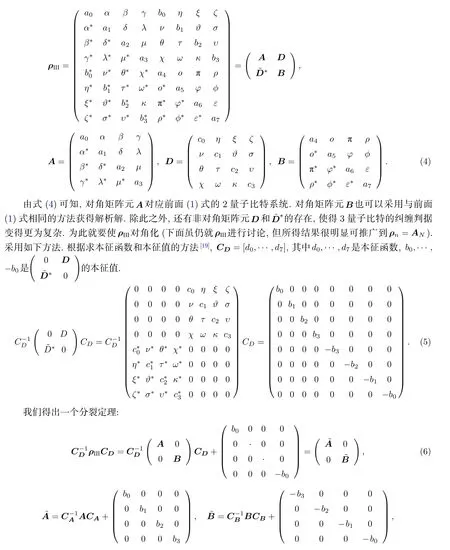
图1 纠缠态的“N-AB-tree 结构”Fig.1.24-AB-tree to four 2 qubit string.

3 量子比特密度矩阵的解析解可以由两个2 量子比特系统密度矩阵表示.n量子比特密度矩阵的解析解可以由两个n–1 量子比特系统密度矩阵表示.即密度矩阵ρn的解析求解转化为ρn−1,A,ρn−1,B.计算过程只需将(7)式的本征函数改写为CD=[d0,···,dN],本征值改写为(b0,···bN/2,b−N/2···b0) ,相应的CA=(d0,···,dN/2) ,CB=(dN/2+1,···,dN).

4 2 量子比特和3 量子比特系统主纠缠态 pp 的数值计算

对于2 量子比特与3 量子比特系统主纠缠态pp的计算分别由图2 和图3—图5 给出.(2)式右端的系数分别表示为a0+a1+a2+a3=r2,a0=0.5×(rcos[θ])2+Δ,a3=0.5(rcos[θ])2−Δ,a1=(rsin[θ]×cos[ω])2,a2=(rsin[θ]sin[ω])2,参照(1)式密度矩阵ρII,a0,a1,a2,a3分别表示对角矩阵元,考虑到参量a0,a3分别为两个二能级原子分别同时取基态或激发态的几率.故a0−a3=2Δ 就代表集居数的差.这个差与驱动场的失谐有关Δω+iγ=(ω21−ω)+i(1/T1+γc) ,T1即纵弛豫时间,γc即碰撞系数[20].

图2 2 量子比特系统主密度矩阵系数 pp 随 { θ,0,0.2} ,{ w,−π,π} 变化的三维曲线图,r =1 (a) Δ =0.002 ;(b) Δ =0.00103 ;(c) Δ =0.0002 ;(d) Δ=0.0001Fig.2.Principal entangled state pp of 2 qubit system with the parameters { θ,0,0.2} ,{ w,−π,π} ,r =1 : (a) Δ =0.002 ;(b)Δ=0.00103 ;(c) Δ =0.0002 ;(d) Δ =0.0001 .

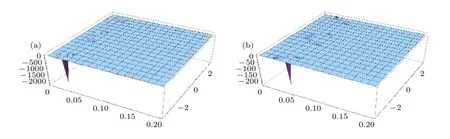
图3 3 量子比特系统主密度矩阵系数 pp 随 { θ,0,0.2} ,{ w,−π,π} 变化的三维曲线图 (a) r a=0.867 ,Δ =0.0001 ;(b) r b=0.547,Δ=0.001,ξ+η=+=1Fig.3.Principal entangle state pp of 3 qubit system with the parameters { θ,0,0.2} ,{ w,−π,π} : (a) r a=0.867 ,Δ =0.0001 ;(b) rb=0.547 ,Δ =0.001 ,ξ +η=+=1 .

图4 3 量子比特系统主密度矩阵系数 pp 随 { θ,0,0.2} ,{ w,−π,π} 变化的三维曲线图 (a) r a=0.724 ,Δ =0.0001 ;(b) r b=0.652,Δ=0.001,ξ+η=+=1Fig.4.Principal entangled state pp of 3 qubit system with the parameters { θ,0,0.2} ,{ w,−π,π} : (a) r a=0.724 ,Δ =0.0001 ;(b) r b=0.652 ,Δ =0.001 ,ξ +η=+=1 .

图5 3 量子比特系统主密度矩阵系数 pp 随 { θ,0,0.2} ,{ w,−π,π} 变化的三维曲线图,r a=rb=0.707 (a) Δ =0.0001 ;(b) Δ=0.0002 ;(c) Δ=0.00103Fig.5.Principal entangled state pp of 3 qubit system with the parameters { θ,0,0.2} ,{ w,−π,π} ,r a=rb=0.707 ;(a) Δ =0.0001 ;(b) Δ =0.0002 ;(c) Δ =0.00103 .

1) 2 量子比特系统

2) 3 量子比特系统

在图2 和图3—图5 描述了2 量子比特和3 量子比特系统的主密度矩阵系数pp的数值计算结果.一般的,存在两种类型的纠缠: 一个是浅纠缠,处于初始阶段,最大值从10 到100;另一个是深度纠缠,处于末了阶段,最大值达到1000.拥有大量的深纠缠的2 量子比特系统.所谓深浅只是对纠缠程度一个唯象的描述,并没严格定义.纠缠对失谐参数的的变化很敏感.图6 描绘出了图2(b)曲线的轮廓.图7 描绘出了图5(c)曲线的轮廓.

图6 和图7 的结果显示曲线的轮廓依赖于纠缠度.在初始阶段,纠缠度从0 逐渐变到100.随后,快速变化到–600 (见图6)和–1400 (见图7).最后,突然返回0.从上面的关系可以获知:

图6 图2(b)曲线的轮廓.Fig.6.The profile of Fig. 2(b).pp vs (Δ=0.00102+x×10−5).

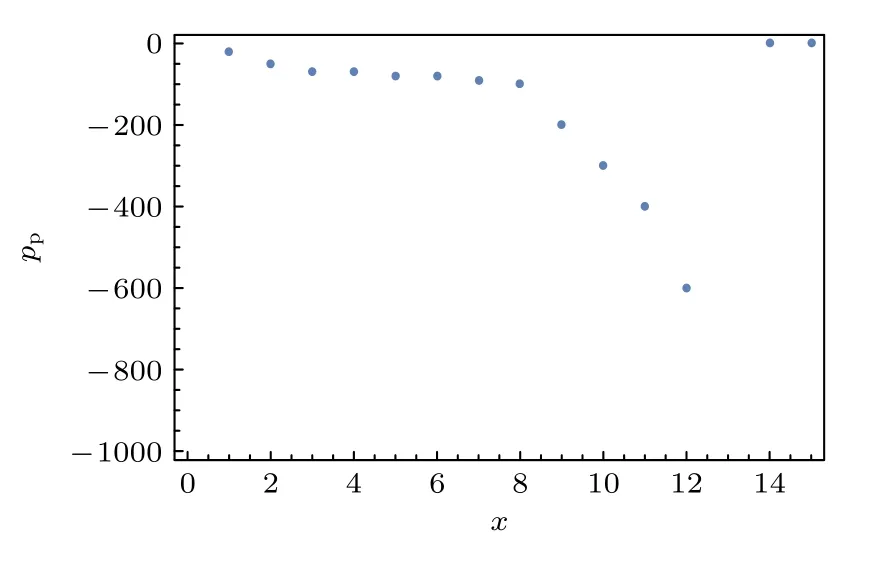
图7 图5(c)曲线的轮廓.Fig.7.The profile of Fig. 5(c).pp vs (Δ=0.00102+x×10−5).

1) 越大粒子量子比特系统会产生更深的纠缠度和更窄的轮廓带宽.

2) 曲线的轮廓与线性色散理论的线型相似[20].使用拉普拉斯变换可以得到纠缠度将随时间τ衰减为∝e−γτ,γ=1/T1+γc为色散曲线的带宽.产生大纠缠的物理条件是上下能级的集居数差即2Δ要求比较小,但不要求反转.

5 结 论

1) 在前文的基础上,我们用同样方法求得3 量子比特系统的主密度矩阵,并发现其结构恰是两个2 量子比特系统的主密度矩阵的对角矩阵.我们称此为A-B分裂.并在这个基础上,应用数学归纳法求得n量子比特系统的主密度矩阵解,我们将其称之为“ 2N-AB-树”.

2) 通过数值计算2 量子比特和3 量子比特揭示出存在2 种类型的纠缠: 浅纠缠和深纠缠,曲线的轮廓具有典型的洛伦兹线型[20].经过对线型的拉普拉斯变换可得出: 1) 纠缠态的衰变时间反比于线型的宽度;2) 线型的宽度又反比于 2n,n为参与纠缠的粒子数.换句话说,参与的粒子数n越大,线型的宽度越乍纠缠态存在时间越长.

附录A 关于(2)式的计算及分离态的矩阵形式

1) (2)式的计算

(1) 式对角化元素相等,有如下的方程:

根据(A1)式—(A4)式,可以得到(2)式:

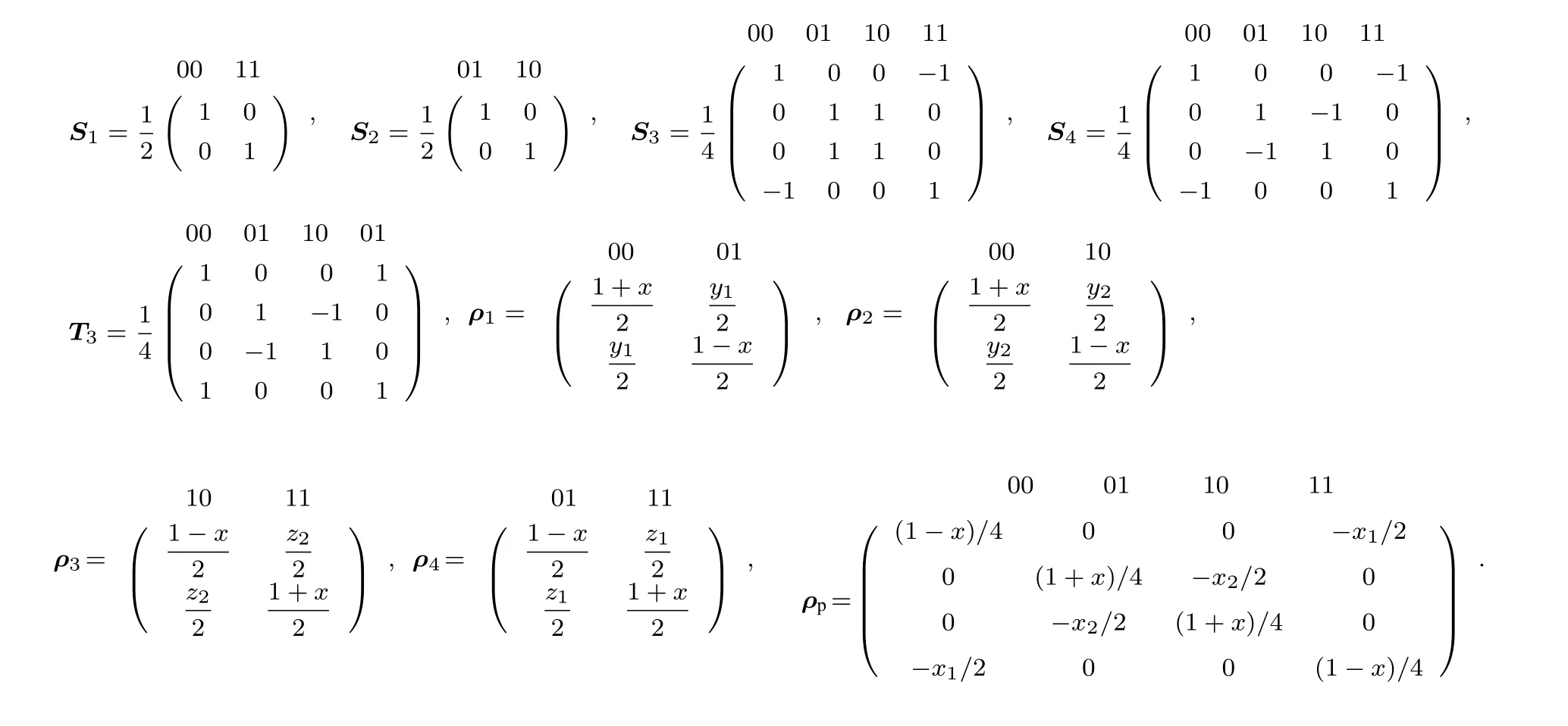
附录B 3 量子系统的基函数,可分离矩阵及主矩阵