基于转换学习的半监督分类
康 昭 刘 亮 韩 蒙
1 (电子科技大学计算机科学与工程学院 成都 611731)2 (电子科技大学公共管理学院 成都 611731) (zkang@uestc.edu.cn)
传统的监督分类只能使用已标记的数据进行训练,而标记样本通常需要耗费大量时间或精力.同时,未标记数据相对容易收集,因此发展能处理它们的算法尤为重要.半监督学习试图处理有大量未标数据的问题,旨在通过学习大量未标记数据和小部分有标签数据来构建更好的分类器.相对而言,半监督学习只需要较少的人力就能达到更高的准确性,在近年来受到了广泛的关注.
在众多半监督分类方法[1-6]中,基于图方法[7-11]的研究是近年来机器学习与模式识别领域的研究热点之一.这类方法通过定义一个图,然后基于图上的局部平滑程度来推断缺失的标签,即若2个样本越相似,它们具有相同标签的可能性就越大.刘钰峰等人[12]在相似样本的类别也相似的一致性假设下,提出图正则化框架对异构图信息网络进行半监督分类.
总的来说,这些方法通常由2步组成.首先,从所有的数据点中构造图,其节点是数据集中有标签和无标签数据样本,而边反映数据间的相似性;其次,假定图上的标签平滑性,利用标签传播方法[13]来推断所有的标签.因此,有大量的算法关注于构建图或标签传播,Jebara等人[14]提出了一种基于b-matching的图构造方法;Cheng等人[15]通过将每个数据点分解为稀疏线性组合来衡量数据点之间的相似性,从而构造图的相似度矩阵;Li等人[16]提出了一种基于低秩子空间的图构造方法;Wang等人[17]提出了一种基于线性邻域的标签传播方法.
尽管现有的算法已经在各种实际应用中取得了不错的效果,但它们依然在某些方面受到限制:
1) 大多数图都是直接基于原始数据上构建的.但由于原始数据的污染,建立的图可能无法准确反映样本之间的潜在关系.而图的质量对于后续任务的执行至关重要[18-19].
2) 现有方法通常将图的构造与标签传播视为2个单独的步骤,这样可能会产生低质量图导致的次优解.即在第1步中构建的图对于后续任务处理可能并不是最优的.
面对上述2个限制,本文提出了一种基于转换学习的半监督分类(semi-supervised classification based on transformed learning,TLSSC)算法.该算法是一个统一的联合优化框架,会根据分类结果更新其他变量.该框架由3个部分组成:1)使用转换学习将原始数据映射到转换空间中;2)借鉴数据自表示思想,在转换空间上学习一个图;3)在图上进行标签传播.
数据自表示的主要策略是将每个数据点表示为其他数据点的线性组合,线性权重将构成相似度矩阵.该思想在子空间聚类问题上取得了巨大成功.研究发现,即使数据不能在原始域中被分割聚类,变换后的数据点也能够被聚类成独立的子空间[20].因此,本文利用转换学习将数据映射到转换空间中,并在转换空间中应用数据自表示进行图的构造.
总的来说,本文的主要贡献有3个方面:
1)提出了一种用于半监督分类的转换学习方式.这种方式将数据映射到一个转换空间,再对转换空间中的数据进行处理,这为表征学习提供了一个新的策略.
2)提出了一种基于转换学习的半监督分类算法框架.该框架将数据映射、图构造和标签传播集成到一个统一的框架中,进行联合优化.
3)在数据集上进行了大量广泛的实验.与现有具有代表性的半监督分类算法相比,本文提出的算法在某些方面展现了其优越性.
为避免混淆,此处将给出本文主要使用的符号.将半监督分类问题的训练数据矩阵表示为X=(x1,···,xl,···,xl+u)T,其中l+u=N,l和u分别是有标签和无标签数据的数目,xi∈Rn为数据样本(数据点),n为特征数.c为数据的类别总数,Y为标签矩阵,当第i个样本属于第j个类别时yij=1,否则yij=0.向量xi=(xi1,xi2,···,xin)∈ Rn的 ℓ2-范数定义为
1 相关工作
1.1 转换学习
传统的字典学习是一个合成过程,它通过从数据中学习一个字典矩阵,利用字典矩阵A对数据进行合成.在数学上,可以这样表示:

而转换学习是字典学习的分析形式,它通过学习一个转换矩阵,将原始数据投影到转换空间内.在数学上,可以这样表示:

其中T是转换矩阵,X是数据矩阵,Z是相关系数矩阵.Ravishankar等人[21]提出了一种转换学习的公式:
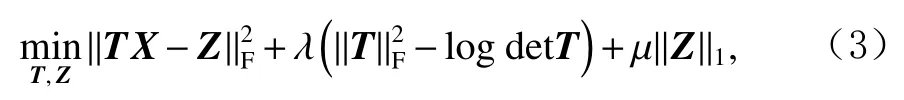
其中参数 λ和 µ为正数.− logdetT能够保证学习到的转换矩阵是满秩的,防止产生退化解,即T= 0,Z= 0.正则化项能够平衡尺度,否则 − logdetT项可以无限增加,产生另一个极端退化解.
Ravishankar等人在文献[22]中提出了一种交替更新的方式解决转换学习问题.具体算法为
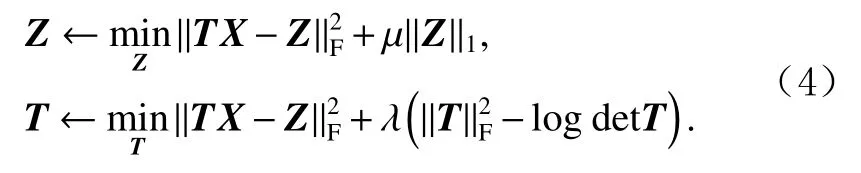
通过软阈值函数直接求解Z:
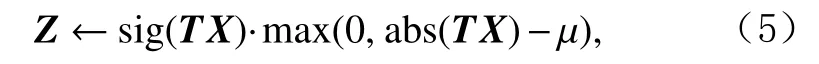
其中“·”表示元素积.对于更新转换矩阵T,可以发现式(4)中各项的梯度都非常容易计算,求导结果为
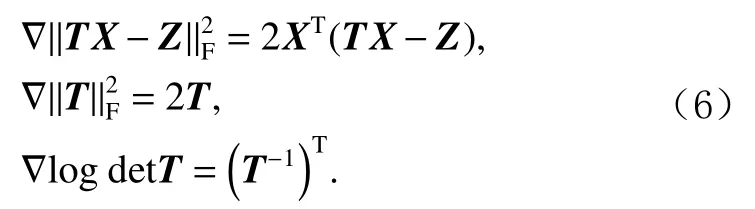
在最初关于转换学习的文献[22]中,提出了一种基于非线性共轭梯度技术来解决转换矩阵的更新问题.接着,在文献[23]中,通过一些线性代数技巧,证明了该迭代更新算法的收敛性.
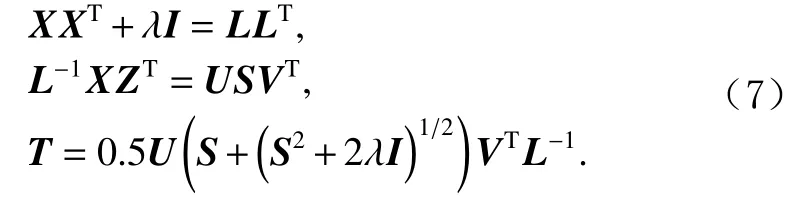
该算法首先进行霍尔茨基分解,XXT+λI是正定对称矩阵,其中I为单位矩阵;接着进行奇异值分解;最后一步对转换矩阵T进行更新.可以发现,L是一个下三角矩阵,因此L−1很容易计算,这极大地减少了计算量,提高了运算效率.由于代价函数是一个单调递减函数,并存在下限,因此代价函数收敛,它的闭式解存在.
1.2 半监督学习
近年来,基于图的半监督分类吸引了广泛关注.例如,Zhu等人[24]设计了一种基于高斯场和谐波函数 (Gaussian field and harmonic function, GFHF)的半监督分类算法,它利用图上的高斯随机场上的谐波特性进行半监督分类.尽管该算法已经取得了广泛的普及,但其分类性能很大程度上仍然取决于输入图.
有一些半监督分类算法关注构造图的鲁棒性对于分类性能的影响.例如,Nie等人[25]提出了一种基于最小化谱嵌入的 ℓ1-范数的半监督分类算法;古楠楠等人[26]提出了一种基于放射子空间稀疏表示的图构造方法,这种方法能够快速对新来样本点进行分类,并且继承了稀疏表示的能够自适应进行邻域选择以及具有较高判别性的优点.
尽管文献[25−26]所提的算法在很多方面已经取得了成效,可以避免直接从嘈杂数据中构造图,但由于图构建和标签传播是分开进行的,其分类性能仍然可能受到影响.
2 基于转换学习的半监督分类
2.1 综合方程
本文提出的算法使用转换学习将原始数据映射到转换空间中,并在转换空间上学习一个图,最后在图上进行标签传播.
本文提出的框架其综合表述为
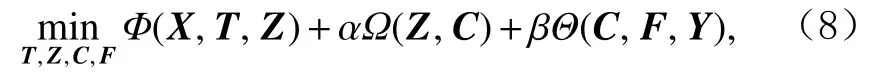
其中,T是转换矩阵,Z表示系数矩阵,C代表一个建立在转换空间上的图的邻接矩阵,F表示标签指示矩阵.α和 β 是参数,用于平衡式(8)的3个函数 Φ (), Ω (),Θ()部分之间的作用.本文将会详细讨论问题(8)中的各项.
2.2 转换学习
本文已经在1.1节讨论了转换学习的现有概念.为了在转换空间中构建一个图并进行标签传播,首先需要从原始数据中学习到一个转换空间:
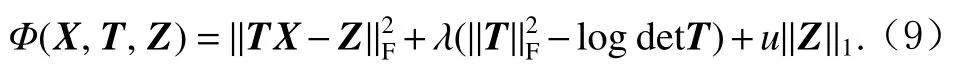
2.3 图构建
式(9)在原始数据X中学习了系数矩阵Z,本节将在系数矩阵Z上建立一个图,Z中每个样本(即每行)对应该图中一个节点.2节点之间的相似度很高(或者相关性很强),则对应的节点之间将存在1条边,这条边的权重正比于样本之间的相似度(或相关性).
定义图的邻接矩阵C=(Cij),其中Cij表示第i行和第j行之间的相似度.本文借鉴数据自表示的思想来建立相似度矩阵[27],其核心思想是数据来自多个子空间,每个样本都可以用同一个子空间的样本的线性组合来表示.数学上,通过式(10)求解:
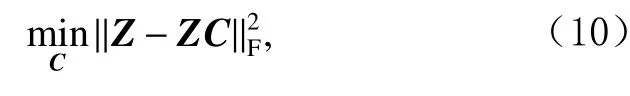
因此,式(8)的第2项可以表示为
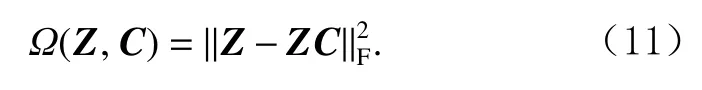
2.4 标签传播
式(11)自动地从数据中学到了一个图,但本文不能保证它对接下来的分类是最优的.理想情况下,如果数据中有c类的话,图C应该恰好拥有c个连通成分.使用 σi表示拉普拉斯矩阵L中第i个最小的特征值.由于L是一个半正定矩阵,所以 σi>0.为了解决这个问题,可以采用定理1:
定理1.图C的连通分量c的个数等于其拉普拉斯矩阵L的零特征值的重数[28].
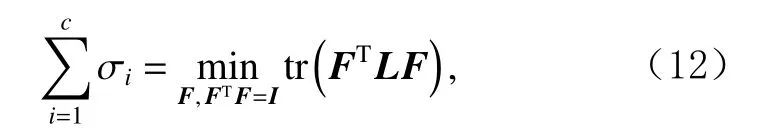
在半监督学习中,矩阵F可以被分解成F=(Fl;Fu)=(Yl;Fu).根据 Nie等人[18]提出的理论,式(12)的等号右边其实就是半监督分类的标签传播目标函数.因此,式(8)的第3项可以表示为
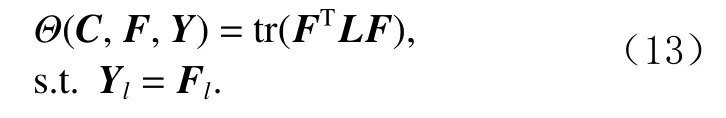
2.5 统一联合优化目标函数
根据式(9)(11)(13),TLSSC 目标函数可写为
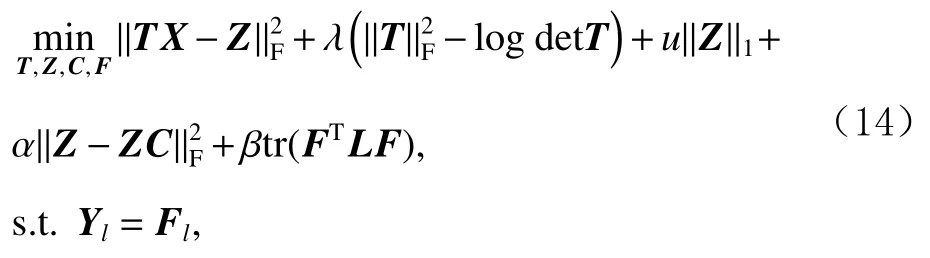
可以观察到,式(14)将转换学习、图构建和标签传播整合到一个统一的框架中,矩阵T,Z,C,F的联合优化有助于实现整体的最优解.系数矩阵Z建立在转换空间中.
3 对式(14)的求解
3.1 优化步骤
本节基于一种交替迭代的策略来求解式(14),即固定某一个变量的同时确定另一个变量.
1)更新转换矩阵T.当固定矩阵Z,C,F后,式(14)变为以下形式:
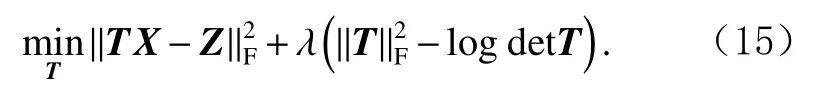
如第1节中所述,式(15)可以通过非线性共轭梯度技术来解决.
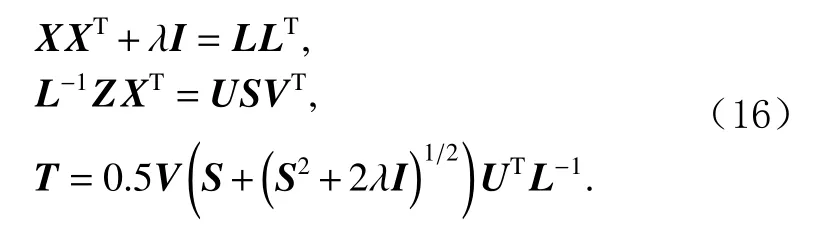
2)更新系数矩阵Z.当固定矩阵Z,C,F后,式(14)转换为:

由于有
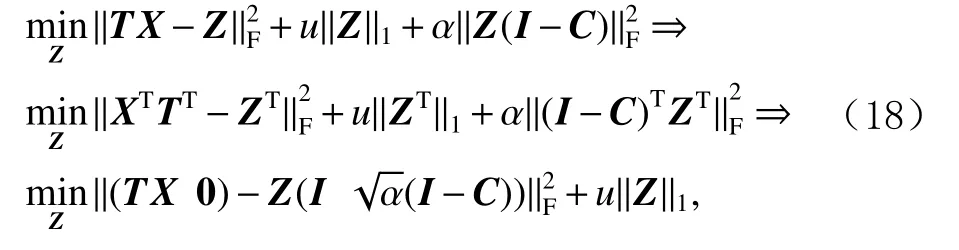
因此式(18)仍可以用软阈值函数进一步求解.
3)更新邻接矩阵C.当固定矩阵T,Z,F后,式(14)转换为:
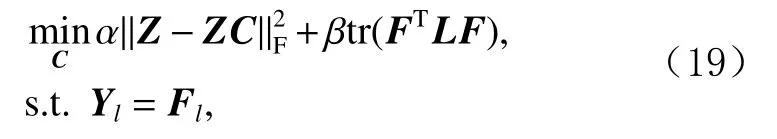
式(19)可以通过逐列来求解,即
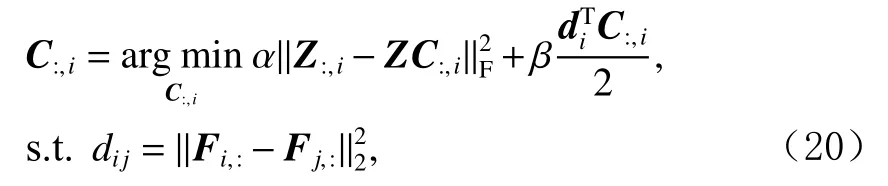
对式(20)进行求解,有
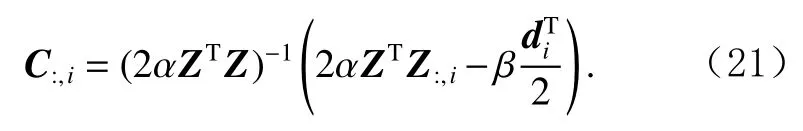
4)更新标签指示矩阵F.固定矩阵T,Z,C后,式(14)转换为:


将上述步骤1)~4)迭代多次,直至F的变化程度小于阈值 ε.最后,未标记的数据点的标签可以通过以下决策函数得到:
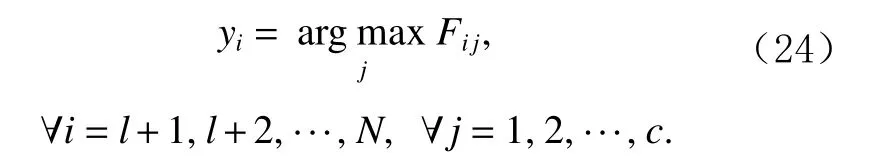
完整的基于转换学习的半监督分类算法如算法1所示.
算法1.基于转换学习的半监督分类算法.
输入;数据矩阵X,标签矩阵Yl,参数 α ,β,λ,µ;
输出:未标记数据的标签.
① 初始化标签指示矩阵Fu,t=0;
② repeat
③t=t+1;
④ 更新转换矩阵Tt根据式(16);
⑤ 更新系数矩阵Zt根据式(18);
⑥ 更新相似度矩阵Ct根据式(21);
⑦ 更新标签矩阵Ft根据式(23);
⑧ until ∥Ft−Ft−1∥2F< ϵ.
3.2 复杂度分析
本文提出的基于转换学习的半监督算法是采用交替迭代的更新策略,给定数据矩阵X∈ Rn×N,固定矩阵Z,C,F,更新转换矩阵T∈ Rm×n,目标方程的各项梯度表达式如式(16)所示.为估算转换学习更新的成本,首先假定XXT已经预先计算,式(16)中的梯度包括了矩阵乘积TXXT和ZXT.计算T(XXT)需要n3次乘加运算,矩阵乘积ZXT在每次更新都会计算,并且当Z是稀疏的且有Nm个非零元素时m=αn(一般 α ≪1),计算ZXT需要 αNn2次乘加操作.接下来式(6)中剩下的梯度计算主要由C3n3决定(矩阵求逆过程),其中C3是一个常数.因此,转换学习更新步骤的计算成本大约为 αNn2+(1+C3)Ln3,其中L通常是固定的共轭梯度步数.假设 (1 +C3)nL<αN,那么每次转换学习更新的成本可以缩放为O(Nn2).每次更新系数矩阵Z∈ Rm×N,使用了 ℓ1−范数,并且使用软阈值求解Z,需要进行O(nN)次操作,同时计算TX(在阈值设定之前)需要O(Nn2)次操作,子空间矩阵计算ZC需要O(N3)次操作,每次更新系数矩阵复杂度为nN+Nn2+N3,n 为了评价本文算法的分类性能,本节在以下3个标准数据集和2个扩充数据集上进行了分类实验. 1)YALE人脸数据库.由耶鲁大学计算视觉与控制中心创建,包含15位志愿者的165张图片,每个对象采集的样本包含11张有明显的光照变化的近额图像.图1(a)展示了一些示例图片. 2)JAFFE人脸数据集.包含10位日本女性志愿者的213张图片,每个对象的样本包含7种不同的面部表情.图1(b)展示了一些示例. 3)COIL20图像数据集.由哥伦比亚大学图像库发布,包含20个物体在360°旋转中不同角度成像的图片,每个对象包含72种姿势.图1(c)展示了一些示例. 4)COIL100图像数据集.包含100个物体,每个物体72张图片在360°旋转中不同角度成像的图片. 5)YALEB.耶鲁大学扩充人脸数据库,总样本数2 414张,共38类,每类大约64张图片,每张图片在不同的光照条件和不同的面部表情下拍摄. Fig.1 Sample images of three datasets图1 3个数据集样本的示例 本节将TLSSC与4种现有具有代表性的算法进行了比较: 1)LGC(learning with local and global consistency)算法.由Zhou等人[30]提出,是一种广泛使用的半监督分类算法. 2)GFHF(Gaussian fields and harmonic functions)算法.它是除了LGC外的另一个流行的标签传播算法. 3)S2LRR(semi-supervised low-rank representation)算法.Li等人[31]提出了一种基于自表达的方法来构建半监督学习图.相似度矩阵和类别指示矩阵交替迭代更新,从而达到互相学习和提高.基于低秩假设,得到 S2LRR 模型. 4)SCAN(semi-supervised classification with adaptive neighbors)算法.Nie 等人[18]提出一种基于图的方法,使用自适应邻近点的方法构造相似度矩阵,将图构造和标签传播集合到一个框架中联合优化. 在上述4种算法中,LGC与GFHF均以拉普拉斯矩阵作为输入.为了使其获得更好的性能,本文基于7种核矩阵计算拉普拉斯矩阵,其中7种核矩阵包含4个形式分别为t∈{0.1,1,10,100}的高斯核、1个形式为K(x,y)=xTy的线性核,以及2个形式为K(x,y)=(α+xTy)2, α ∈{0,1}的多项式核.另外2种算法则直接从原始数据中构建图. 所有算法均选择10%,30%,50%有标签的数据,重复实验20次,将分类准确度(accuracy,Acc)和标准差记录于表1中.所有算法都选择了在最好参数下的结果,LGC和GFHF算法选择了在最好的核矩阵下产生的结果.结果显示,当标签比例增大时,所有方法的分类准确度都有所上升,在大多情况下,TLSSC算法的分类性能比其他现有算法更好,尤其在YALE数据集上得到了大量的提升.另外,相对于紧密相关的S2LRR算法,TLSSC在大部分情况下也大大提升了分类性能,尤其是在YALE和COIL100数据集上. 图2展示了邻接矩阵C在3个数据集上的分布,可以发现C几乎可以被视作为块对角矩阵,这符合本文的预期,说明了在数据集上学到的图能很好地反映样本间的关系. Table 1 Experimental Results of Classification Accuracy for Each Algorithm on Benchmark Data Sets表1 各种算法在数据集上的Acc实验结果 % Fig.2 Distribution of the adjacency matrix Con 3 datasets图2 邻接矩阵 C在3个数据集上的分布 为了测试TLSSC算法对参数α,β,λ,μ的敏感性,文本以JAFFE数据集为例,在图3中给出了在λ=0.000 1,μ= 0.000 01 时,不同α和β在不同标签比例下的实验精度.可以发现,当标签比例减小时,分类准确率有所下降;在标签比例较小时,参数α和β的变化对分类结果影响较大.而图4 给出了在α= 0.000 1,β=0.000 1 时,不同λ和μ在不同标签比例下的实验精度.图4的结果显示,λ的变化对分类结果的影响更小,而且在μ取较小的值时性能相对好一些. Fig.3 Influence of α and β on Acc in JAFFE dataset图3 α和β在JAFFE数据集上Acc的影响 Fig.4 Influence of λ and μ on Acc in JAFFE dataset图4 λ和μ在JAFFE数据集上Acc的影响 本文提出了一种基于转换学习的半监督分类算法,该算法提出了一个统一联合优化框架.该框架首先利用转换学习,将原始数据映射到一个数据平面(转换空间);接着借鉴数据自表示思想,在转换空间中构建了一个图,并在图上进行标签传播.该框架集成了转换学习、图构建和标签传递3个步骤,联合统一优化有利于获得全局最优解.实验表明,本文提出的TLSSC算法在大部分情况下优于其他现有分类算法,证明了该算法的有效性. 作者贡献声明:康昭负责论文方案设计实施、实验结果整理与分析以及论文整体攥写和修订;刘亮和韩蒙负责论文撰写与修订.4 实 验
4.1 数据集
4.2 对比算法
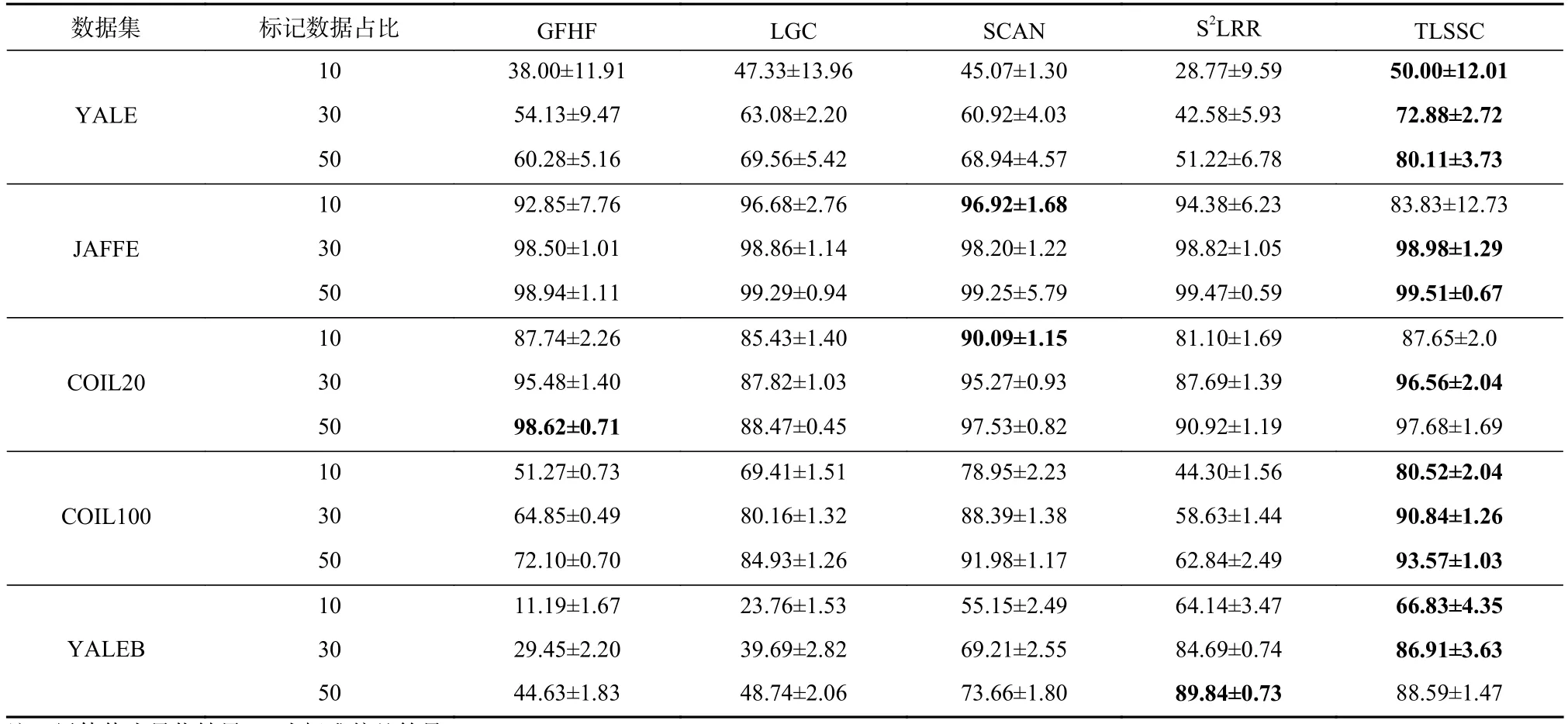
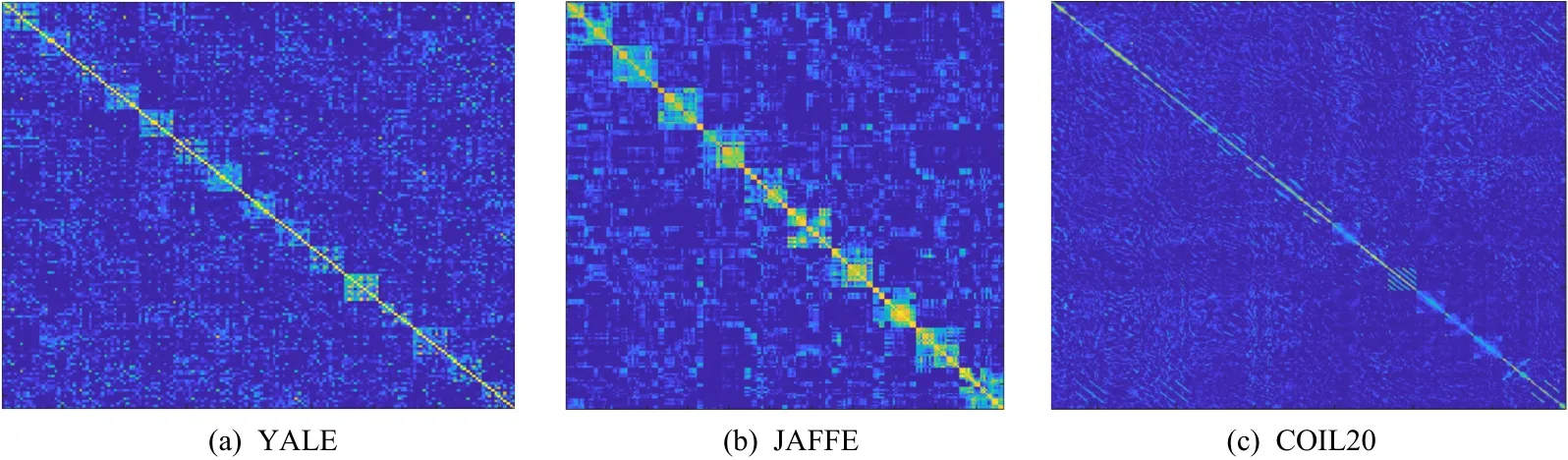
4.3 结 果
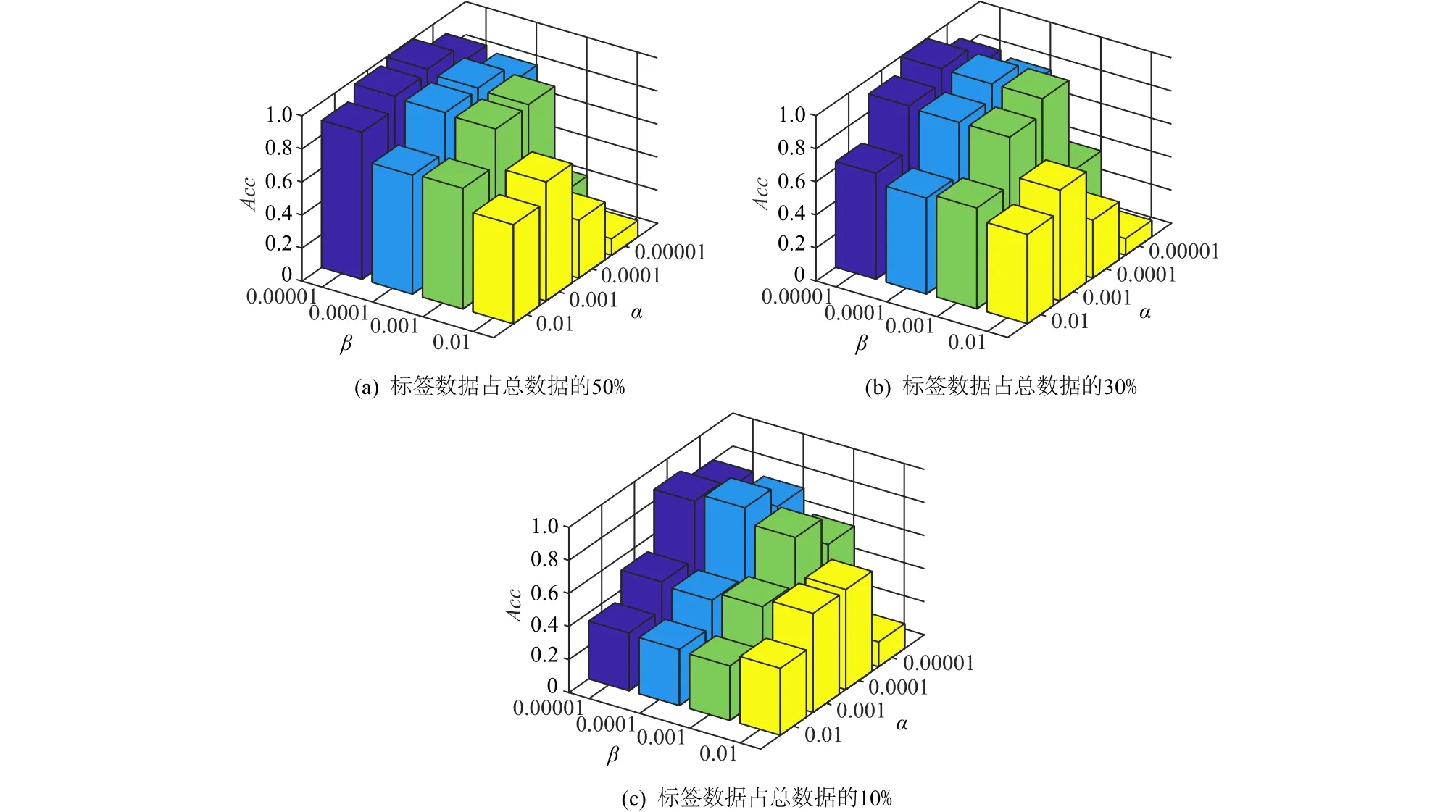
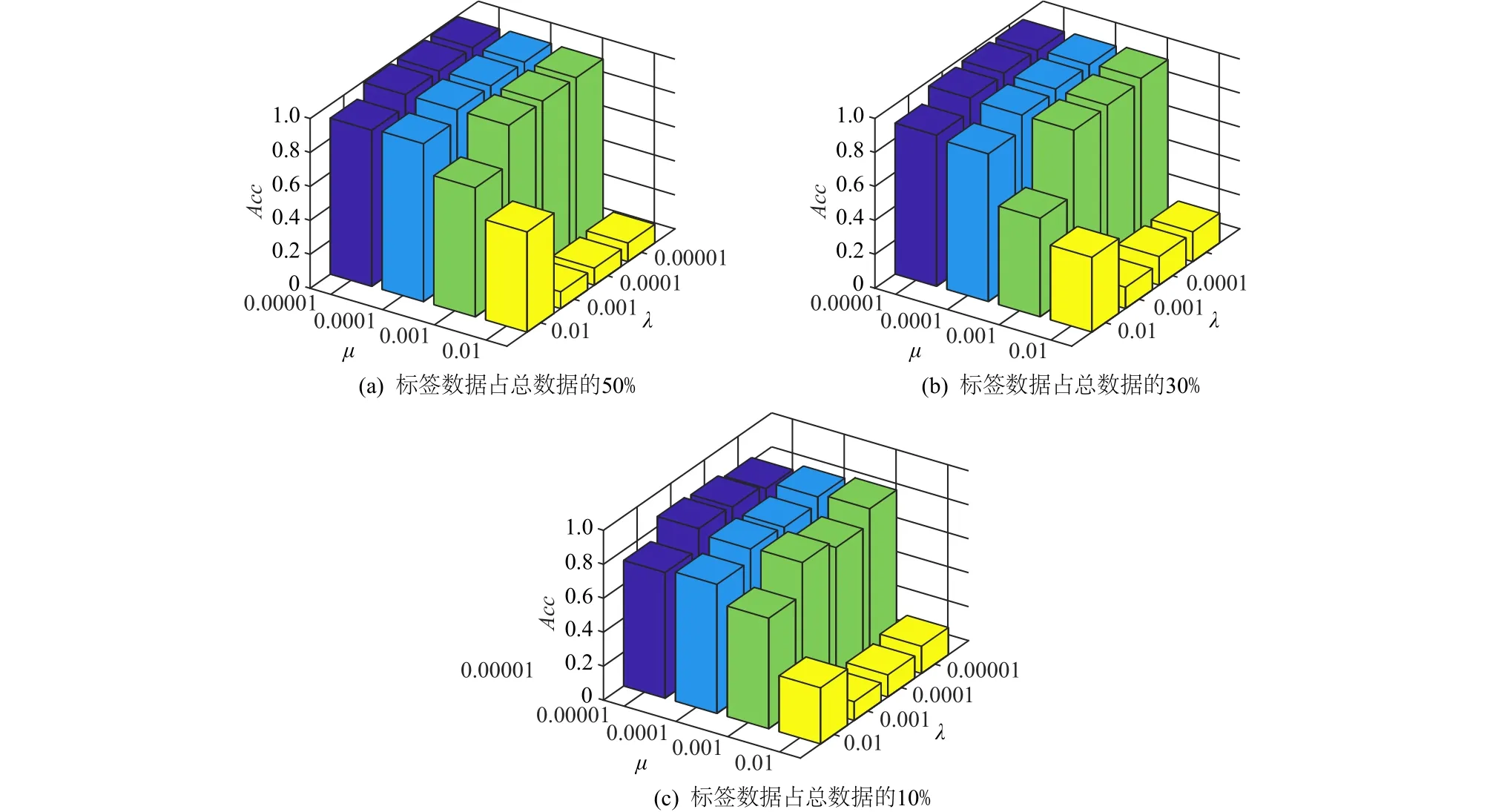
4.4 参数敏感性
5 总 结

