基于自适应k近邻的时间序列异常模式识别
王 玲 周 南 申 鹏
(北京科技大学自动化学院 北京 100083)
(工业过程知识自动化教育部重点实验室(北京科技大学) 北京 100083)(lingwang@ustb.edu.cn)
目前,时间序列的异常检测作为一项重要的数据挖掘任务,已被广泛应用到气象信息[1]、水文监测[2]、医疗保健[3]、工业应用[4]等众多领域中.根据异常的表现形式不同,时间序列的异常可以分为异常点、异常序列及异常子序列[5].异常点是与大部分数据点有显著差异的数据点[6-7];异常序列指的是与大部分时间序列有显著偏差的整条时间序列[8-9];异常子序列是与大部分子序列有显著不同的子序列[10-11].考虑到异常子序列可能与一段时间内的特殊事件有关,往往会比正常子序列包含更多有用的信息,更有研究价值,本文主要对异常子序列进行研究.
异常子序列并非只有一种,不同的机制[12]会导致多类异常子序列的产生.例如,心电图的异常子序列即心率失常,可以分为窦性心动过速、早搏、房颤、窦性心动过缓、房室传导阻滞等多种类型;水文时间序列中的异常子序列也可以分为洪水、干旱等多种异常类型.为了识别不同类型的异常,可以先检测异常子序列,然后再利用聚类算法区分异常子序列的类型,令一个异常模式代表一类异常子序列,进而实现异常模式的识别.下面分别对异常子序列检测和异常子序列聚类这2部分的相关工作进行说明.
目前, 常见的异常子序列检测算法包括基于距离的异常子序列检测方法[13-15]、基于聚类的异常子序列检测方法[5,16]、基于密度的异常子序列检测方法等[17-18].基于距离的异常子序列检测方法利用子序列之间的距离计算子序列的异常分数(异常因子), 通过比较异常分数与设定阈值的大小来检测异常子序列.文献[13]提出一种基于距离的异常子序列检测算法DBAD,通过计算两两子序列的欧氏距离,并比较其与分布中心的偏差程度实现异常子序列检测.文献[15]将子序列与其最近的k个子序列距离的平均值作为异常分数,并利用假设检验确定子序列是否异常.基于聚类的异常子序列检测方法是将子序列划分到不同的类簇中,使得簇中的子序列具有较高相似度,簇间的子序列具有较低相似度.通过分析子序列和类簇中心之间的关系,来寻找异常子序列.文献[16]使用模糊c均值聚类[19]来揭示子序列的结构,然后利用从簇中心和划分矩阵得到的重构准则[20]重建原始子序列,对于每个子序列,根据原始子序列与重建子序列的差值分配其异常分数.该聚类算法需要人为设置聚类个数,但在实际应用中,我们通常缺少对数据集的先验知识,这会严重影响聚类的效果.而基于密度的异常子序列检测方法是根据子序列的密度与其周围子序列的密度之间的比值来定义异常分数,从而检测出异常子序列.文献[18]提出了一种动态局部密度估计(dynamic local density estimation, DLDE)异常子序列检测算法,利用时间分割树 (time split tree, TSTree)动态分割时间序列,并通过子序列中每个数据点的动态局部密度来评估子序列的异常程度;但该算法需要利用集成学习获取参数,算法复杂度较大.
由于不同结构的异常子序列预示着不同的异常事件,因此需要对异常子序列进行聚类以区分不同类型的异常子序列,识别所有异常模式.这里介绍一些可用于聚类异常子序列的时间序列聚类算法.文献[21]提出了一种基于轨迹形状的时间序列聚类算法kmlShape,该算法是k均值聚类算法[22]的一个变体,利用弗雷歇距离计算出时间序列之间的距离,并提出弗雷歇平均值确定每个类别的均值以实现时间序列的聚类;文献[23]提出一种基于统计预处理的距离密度聚类DDC,将平滑和特征选择作为预处理步骤,在每个特性集群中进行距离密度聚类以完成时间序列聚类;文献[24]提出了一个新颖的时间序列聚类算法,该算法可以生成同质且较好分离的聚类,其采用标准的互相关距离度量方法并基于此提出了一个计算簇心的算法,在每一次迭代中都用其来更新时间序列的聚类分配.然而,这些聚类算法对输入参数较为敏感,影响最终聚类结果的正确性,这在一定程度上限制了这些聚类算法的应用.
文献[21−24]中提出的算法在设置参数方面较为薄弱,且忽略了异常子序列的类别区分问题,因此,本文重新定义了异常模式这一概念,提出一种基于自适应k近邻的异常模式识别算法(anomaly pattern recognition algorithm based on adaptiveknearest neighbor, APAKN).该算法首先根据各子序列的自适应k近邻计算其自适应距离比和相对密度,这里相对密度与传统基于密度的异常检测算法[25]的局部密度有所区别,无需计算待测对象密度与其邻域对象密度之比;然后提出一种基于最小方差的自适应阈值方法确定异常阈值;最后采用基于自适应k近邻的聚类算法自动发现聚类中心并聚类异常子序列.整个算法过程在无需设置任何参数的情况下,不仅解决了密度不平衡问题,还精简了传统基于密度异常子序列检测算法的步骤,实现良好的异常模式识别效果.
1 相关定义
定义1.子序列.给定一子序列集合D={s1,s2,…,, 其中为子序列的个数其中表示子序列所包含的数据点个数.
定义2.异常子序列和正常子序列.异常子序列是子序列集合中异常分数大于异常阈值的子序列,异常子序列集合表示为其中n为异常子序列的个数, 则正常子序列的个数为N−n,正常子序列集合表示为
定义3.异常模式.异常模式是由相似异常子序列构成的类簇的中心, 异常模式集合表示为P={p1,p2,…,pi,…,pc},其中c为聚类后的类簇个数.
定义4.子序列距离.对于子序列集D中任意2个子序列si,sj, 采用动态时间弯曲(dynamic time warping,DTW)距离[26]度量计算si与sj之间的距离
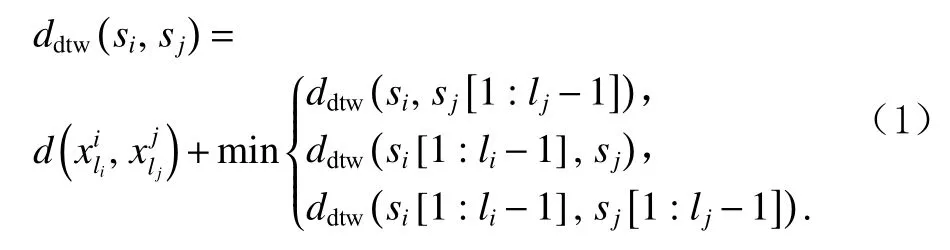
其中,si[1:li−1]为si去除尾元素后剩余的子序列,即去除尾元素后剩余的子序列,即表示数据点与数据点之间的欧氏距离,计算方法为 √
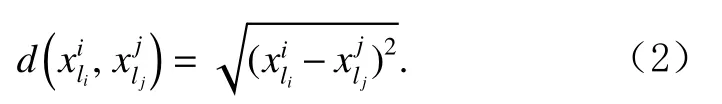
定义5.第k近 邻 和 第k近 邻 距 离.假 设si和sj为 子序列集D中 的子序列,对于任意正整数k,si的第k近邻为sj,si的 第k近 邻 距 离 为si与sj之 间 的 距 离,记为kdk(si),sj需要满足2个条件:
1)D中 至 少 存 在k个 子 序 列sj′, 使kdk(si)成立;
2)D中 最多存在k−1个子序列sj′,使kdk(si)成立.
定义6.k近邻域.子序列集合D中 ,除si外所有与si的距离小于等于si的第k近邻距离kdk(si)的子序列构成子序列si的k近邻域KNNk(si),即

将KNNk(si)中子序列的个数定义为si的k近邻个数,记为 |KNNk(si)|.
定义7.反向k近邻域.对于任意子序列,如 果si属 于sj的k近 邻 域 , 则sj属 于si的 反 向k近 邻 域RNNk(si),即
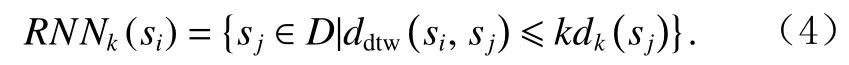
将RNNk(si)中子序列的个数定义为si的 反向k近邻个数,记为 |RNNk(si)|.
为说明k近邻域和反向k近邻域,图1利用7个空心圆分别表示7个子序列,显示出各子序列之间的距离关系.表1列出近邻值k=4时7个子序列的k近邻域、反向k近邻域、反向k近邻个数.
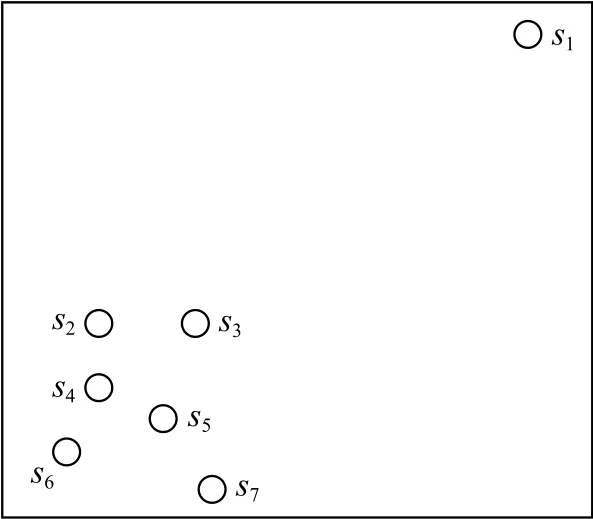
Fig.1 Schematic diagram of subsequence distribution图1 子序列分布示意图

Table 1 k Near Neighbors Domain and Reverse k Near Neighbors Domain of Subsequences when k = 4表1 k = 4时子序列的k近邻域与反向k近邻域
从表1可以看出,同一子序列的k近邻域和反向k近邻域并不存在对称关系.
2 基于自适应 k近邻的异常模式识别算法
APAKN是一个基于自适应k近邻的异常模式识别算法,算法整体工作流程如图2所示,主要由异常子序列检测和异常子序列聚类2个部分组成.本节将对 APAKN 算法的基本思想及其实现过程进行详细介绍.
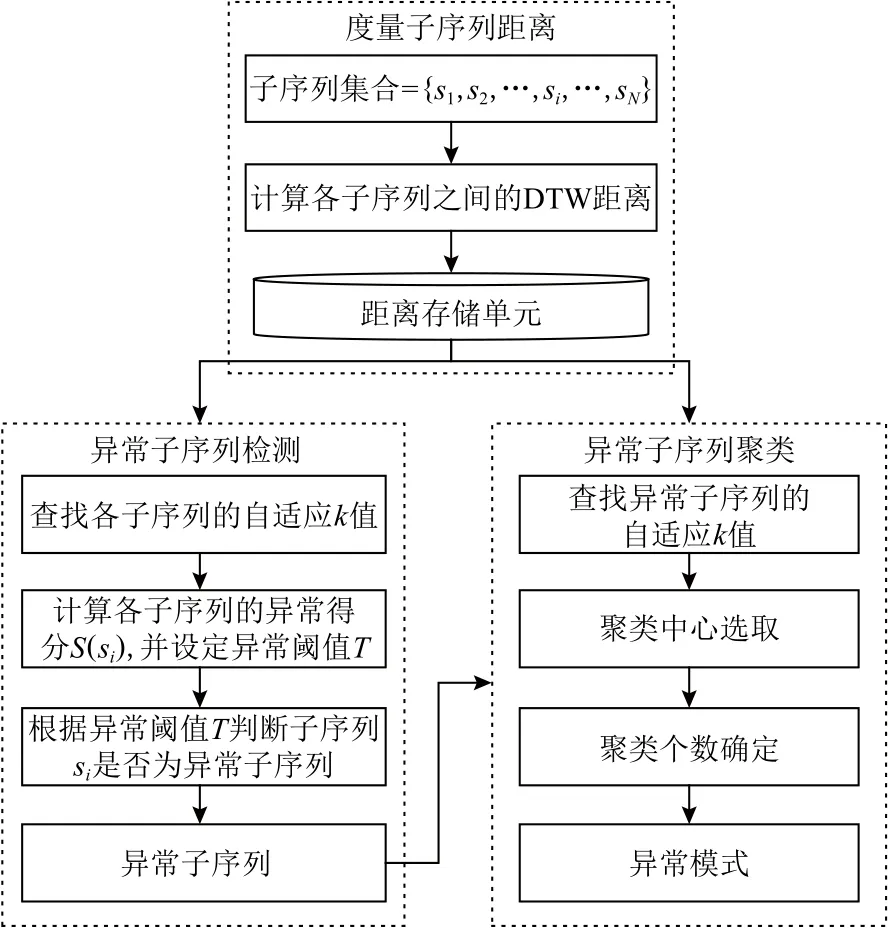
Fig.2 The overall workflow of the APAKN图2 APAKN的总体工作流程
2.1 基于相对密度的异常子序列检测
为了确定子序列是否异常,查询各子序列的自适应k近邻值计算子序列的相对密度,根据相对密度计算异常分数,将异常分数大于异常阈值的子序列视为异常子序列.
考虑到异常子序列具有较少的邻居,正常子序列具有较多的邻居,各子序列的k近邻值并不相同是自适应k近邻搜索算法区别于传统k近邻[27]算法的主要特征.搜索子序列si(si∈D)的自适应k近邻值ki的主要过程为:令搜索次数r=1,迭代地寻找每个子序列的r近邻 域,使用Numr记 录 第r次迭代时集合中0的个数.若Numr在连续3次迭代中未发生变化,即Numr=Numr+1=Numr+2,则认为算法达到稳定状态,迭代停止,否则,令r=r+1继续迭代.将迭代停止后的迭代次数计为kf=r+2,子序列si的 自适应k近邻值
以图1中的子序列为例查找各子序列的自适应k近邻值.图3展示了7个子序列在r=1,r=2,r=3,r=4时的近邻情况.
当r=1时, 图3 (a)展示了所有子序列的 1近邻,其 |RNN1(si)|=0的子序列为s1,s6,s7, 此时Num1=3.
当r=2 时,图3 (b)展示了所有子序列的2近邻,{|RNN2(si)|}i=1={0,3,2,3,4,1,1} ,其 |RNN2(si)|=0 的子序列为s1, 此时Num2=1.
当r=3 时, 图3 (c)展示了子序列s1,s5的3近邻,{|RNN3(si)|}7i=1={0,4,3,5,6,2,1},其 |RNN3(si)|=0的子序列为s1, 此时Num3=1.
当r=4 时, 图3 (d)展示了子序列s1,s5的4近邻,{|RNN4(si)|}7i=1={0,4,5,6,6,4,3},其 |RNN4(si)|=0的子序列为s1, 此时Num4=1.
当r=2 时满足Num2=Num3=Num4, 搜索停止,kf=r+2=4, 输出所有子序列的自适应k值为{k1,k2,…,k7}={0,4,5,6,6,4,3}.
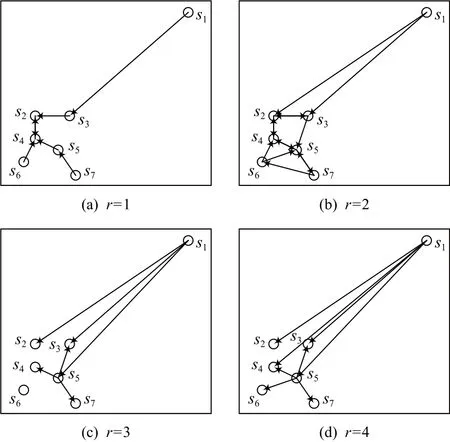
Fig.3 Neighbors of subsequences at different values of r图3 子序列在不同 r值时的近邻情况
在得到子序列si(i=1,2,…,N)的自适应k近邻值ki(i=1,2,…,N)的基础上,计算子序列的相对密度来进一步得到子序列的异常分数.许多复杂的数据集可能有多个密度不同的集群,如果只比较局部密度的大小可能会将一些密度较小集群中的数据对象误检为异常.为解决密度不平衡问题,目前基于密度的异常子序列检测算法通常在估计出所有子序列的局部密度后,通过比较待测子序列的局部密度与其邻域内子序列的局部密度来检测异常,但算法结果对邻域参数较为敏感,人工选择合适的邻域参数较为困难,需要研究者的经验或大量的实验,也使算法不具备自适应性.为此,本文引入自适应距离比计算相对密度,不仅解决密度不平衡问题,而且无需人为选择近邻参数.
令km为集合 {k1,k2,…,kN}中的最大值,为子序列si的km近邻域中的子序列,为子序列的自适应k近邻值,si与的距离为,的第近邻距离为,计算si与其km近邻域KNNkm(si)内所有子序列的自适应距离比.子序列si相对于子序列的自适应距离比为
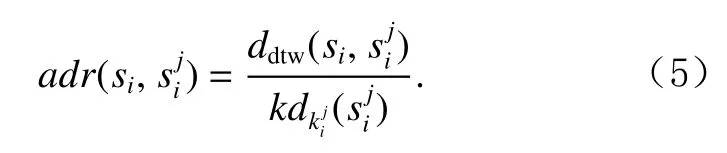
计算子序列si(si∈D)的相对密度,其为si与其所有KNNkm(si)内子序列的平均自适应距离比的倒数,KNNkm(si)中的子序列个数用表示.si的相对密度计算公式为
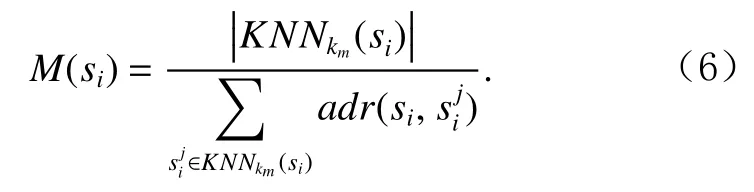
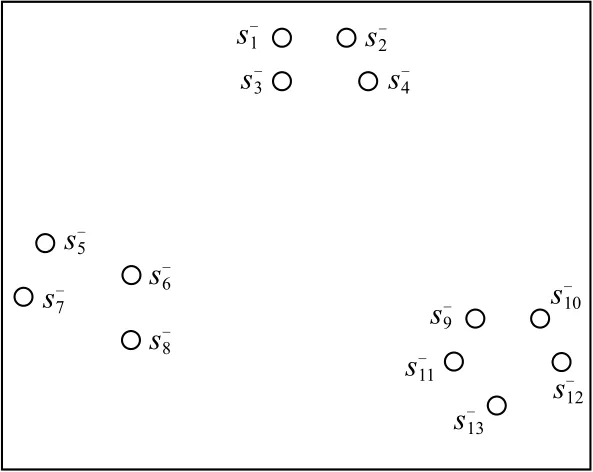
以图4为例说明自适应距离比如何解决密度不平衡问题.图4中s8,s9,s10属于高密度集群,s11为异常子序列,s12,s13,s14,s15,s16属于低密度集群.若是单纯将密度小的子序列视为异常,则低密度集群都有可能被视为异常.这里以s8,s11,s14为例证明自适应距离比解决密度不平衡问题的有效性.在该示例中km=8,图4中已标注出s8,s11,s14的8近邻域范围,表2列出km=8时s8,s11,s14相对于其第8近邻的自适应距离比.
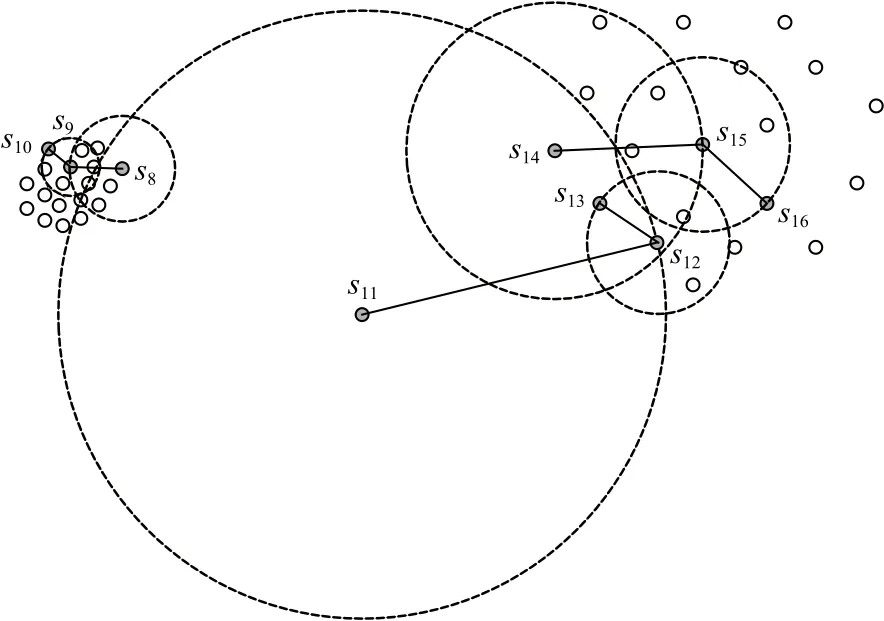
Fig.4 Density imbalance data图4 密度不平衡数据

Table 2 Adaptive Distance Ratio of s8, s11, s14 Relative to Its 8th Nearest Neighbor表2 s8, s11, s14相对于其第8近邻的自适应距离比
从表2可以看出adr(s8,s9)与adr(s14,s15)相差较小,而adr(s11,s12)远大于adr(s8,s9)和adr(s14,s15),根据相对密度的计算公式(6)可以推断出M(s8)与M(s14)的值大致相同,而M(s11)远小于M(s8)和M(s14)的值.这可以证明本文提出的自适应距离比和相对密度不受其所属集群密度的影响,解决了密度不平衡问题.
子序列相对密度较低意味着其可能具有较高的异常分数.进一步,子序列si的异常分数为
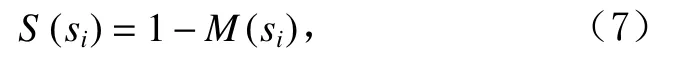
得到异常分数集合S={S(s1),S(s2),…,S(si),…,S(sN)}后,对其做归一化处理,子序列si的最终异常分数为
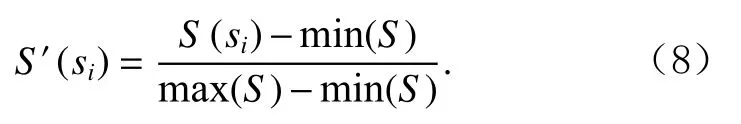
以图1中s1为例计算异常分数:由于{k1,k2,…,k7}={0,4,5,6,6,4,3},所以该集合中的最大值km=6,为子序列s1的6近邻域中的子序列,即(j=1,2,…,6)∈KNN6(s1)={s3,s2,s5,s4,s7,s6},为子序列的自适应k近邻值,s3,s2,s5,s4,s7,s6的自适应k近邻值分别为5,4,6,6,3,4,s3,s2,s5,s4,s7,s6的第近邻分别是s6,s6,s1,s1,s4,s7,因此的第近邻距离分别为ddtw(s3,s6),ddtw(s2,s6),ddtw(s5,s1),ddtw(s4,s1),ddtw(s7,s4),ddtw(s6,s7);代入式(6)可以得到M(s1)=0.413,s1的原始异常分数为S(s1)=1−M(s1)=0.586,归一化异常分数为S′(s1)=1,后文中若无特殊说明,异常分数即是指归一化后的异常分数.
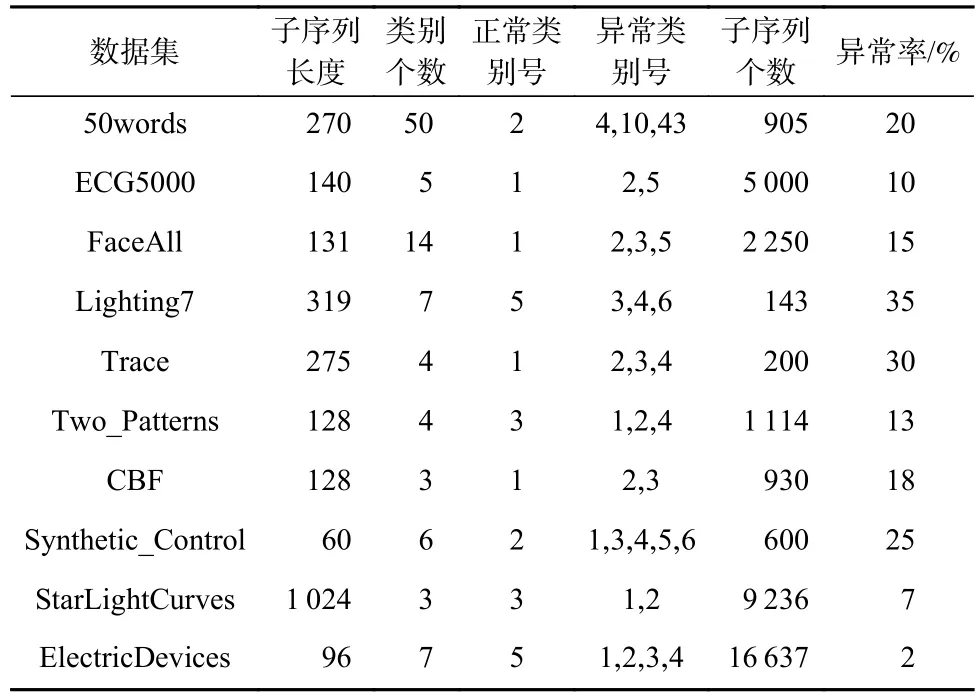
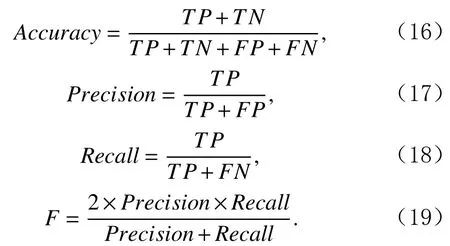
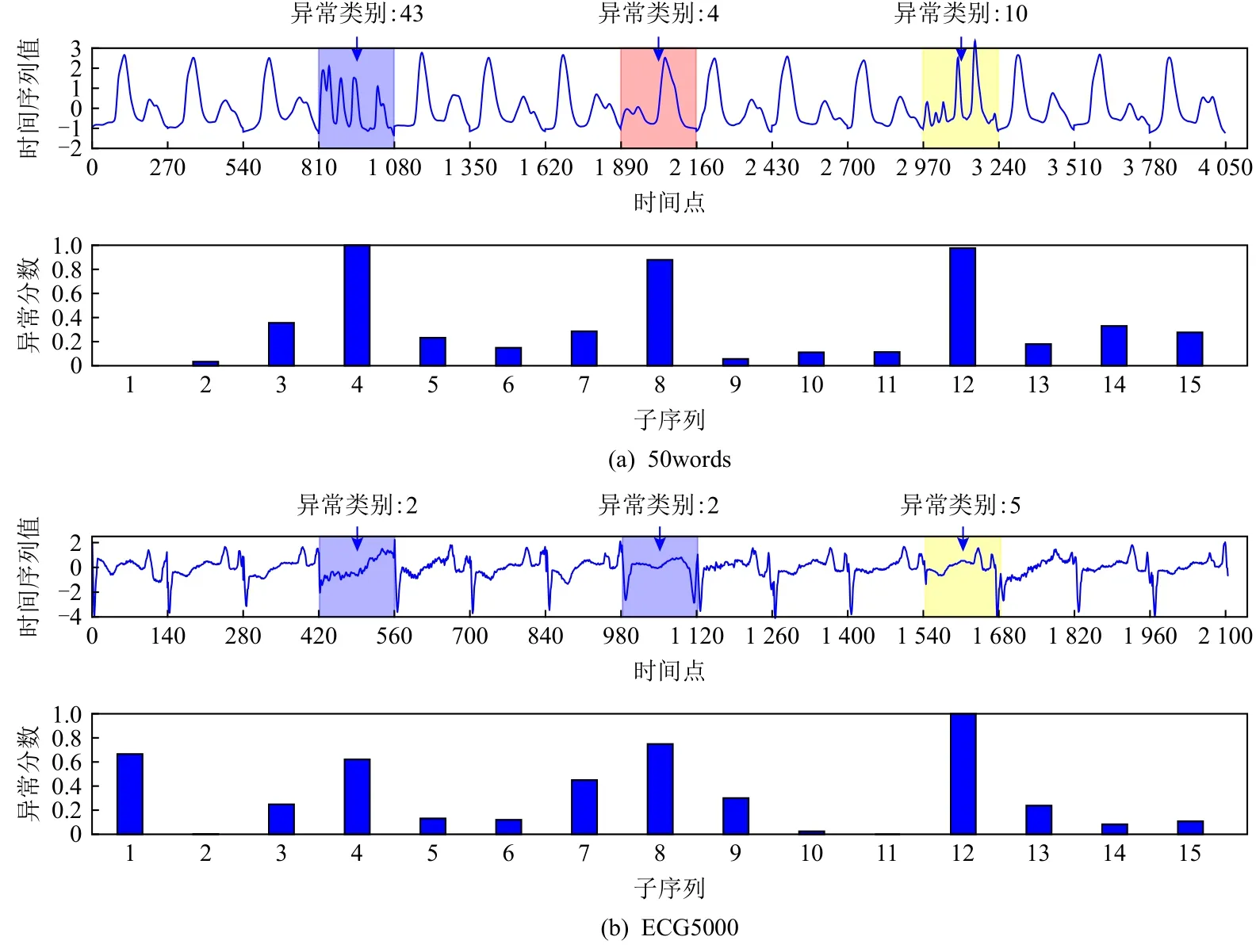
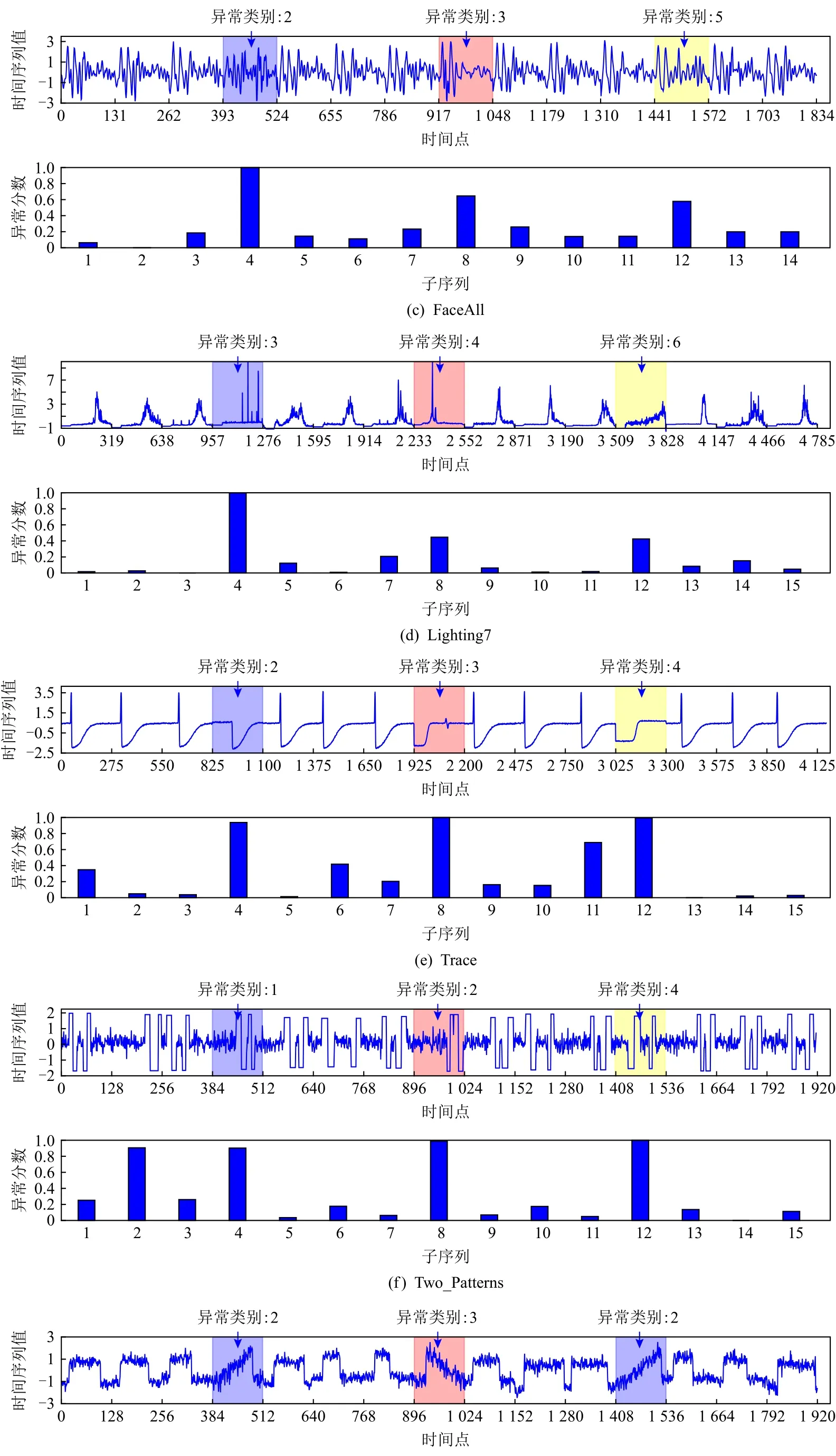
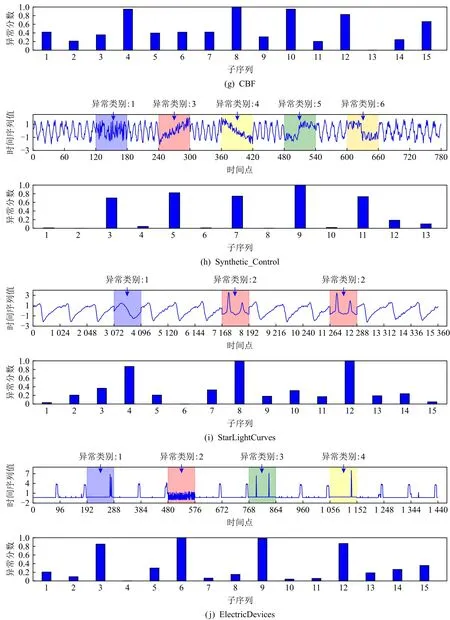
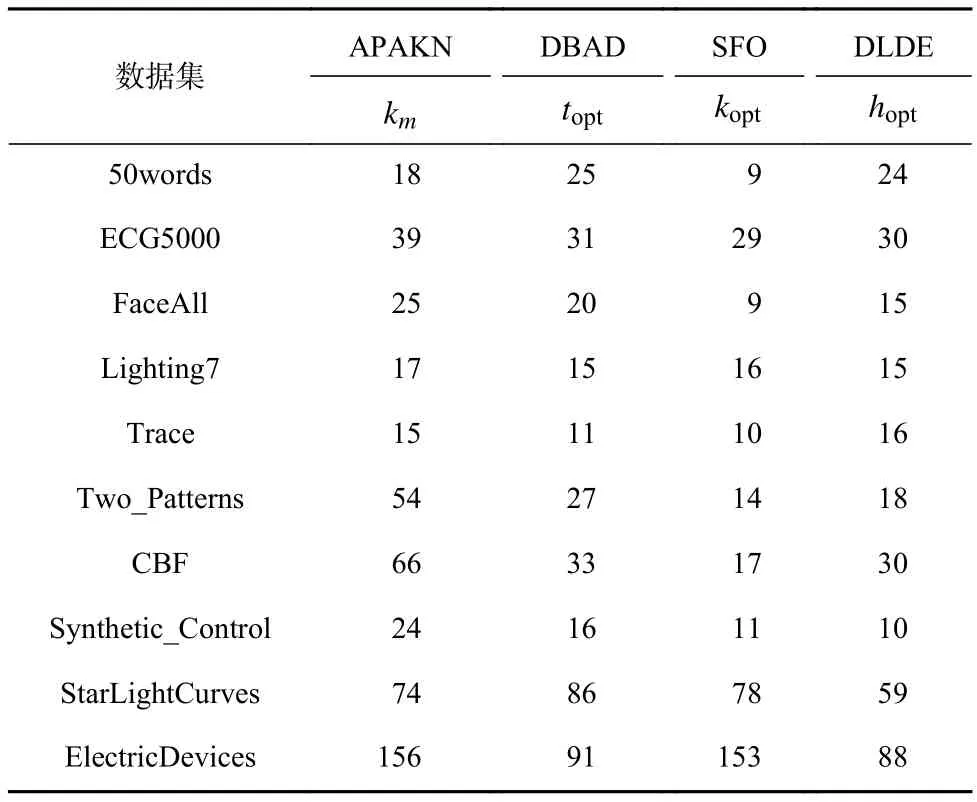
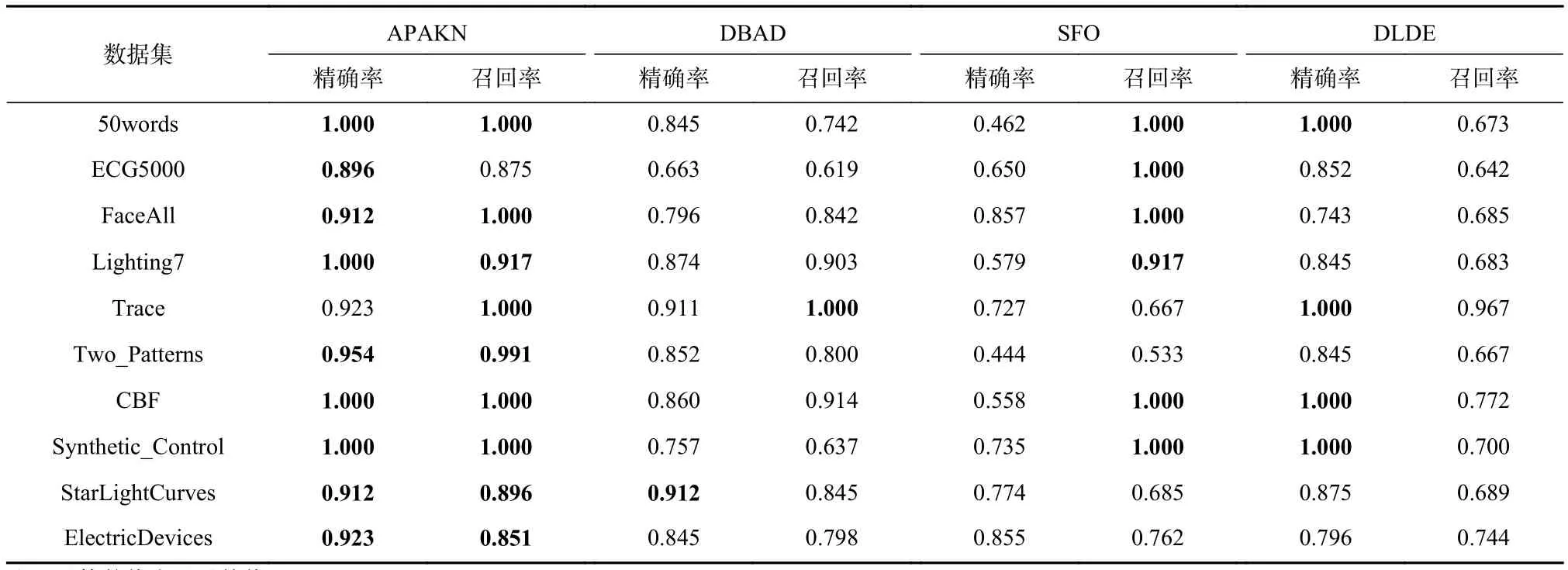
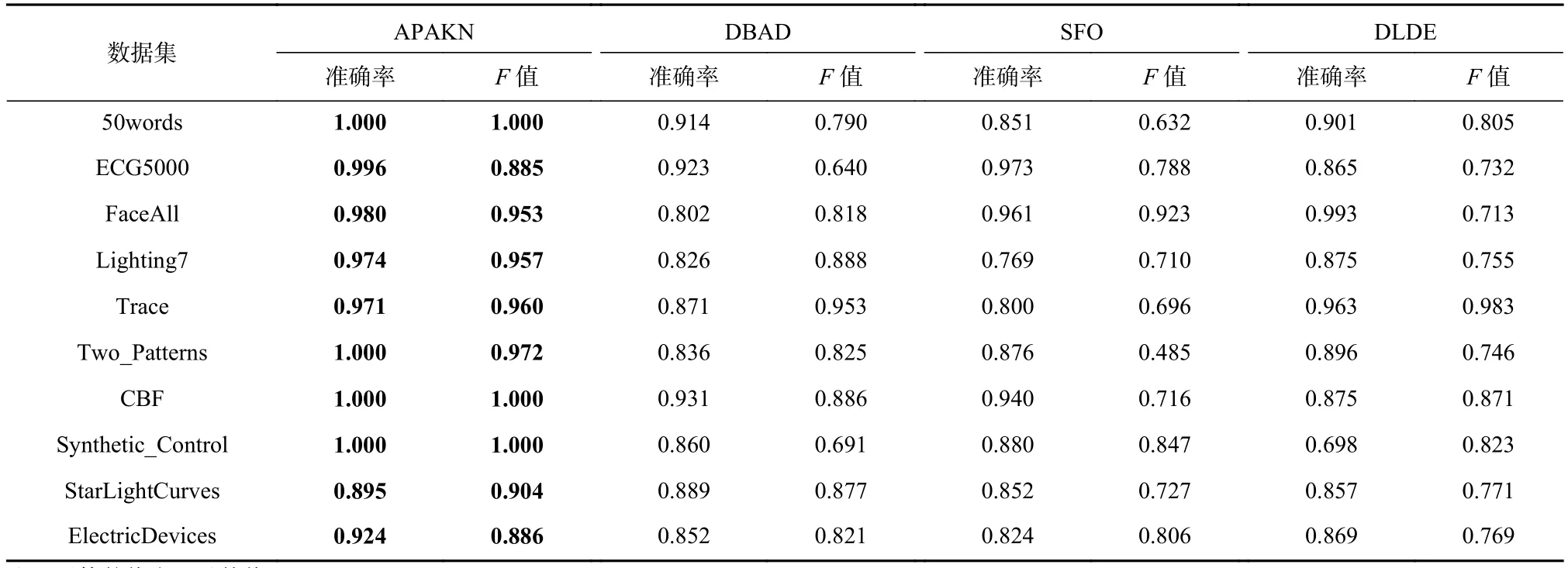
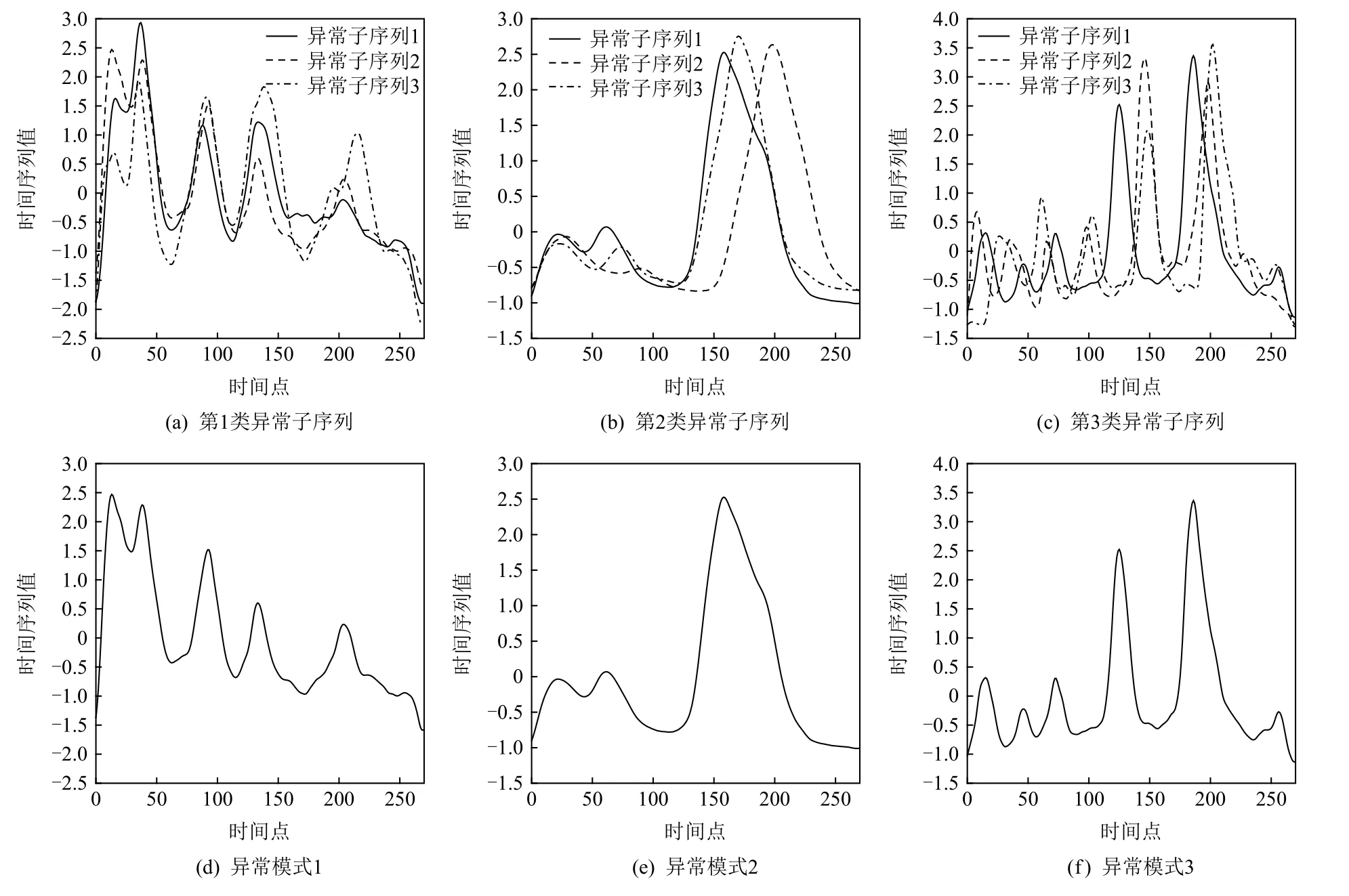
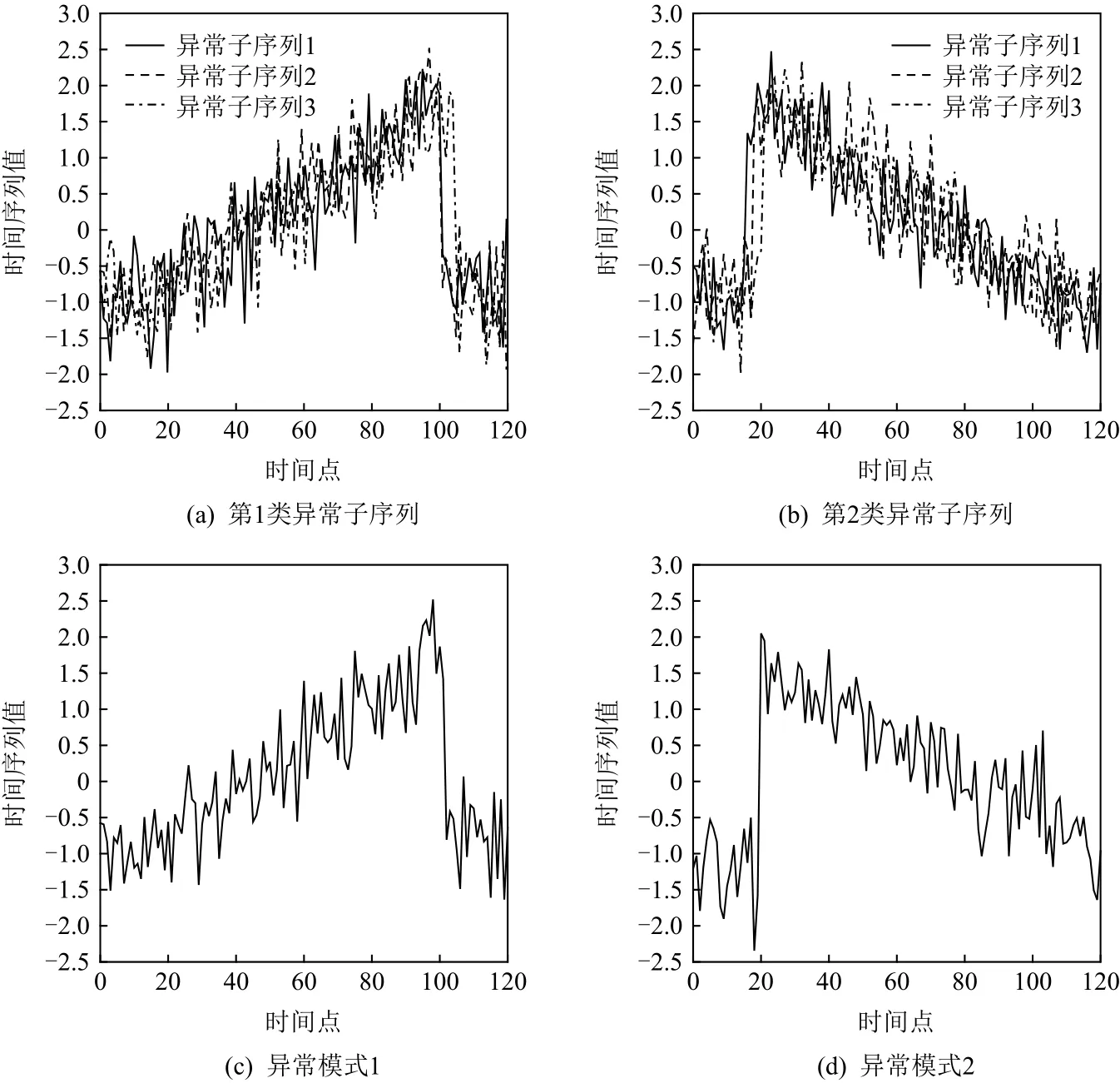
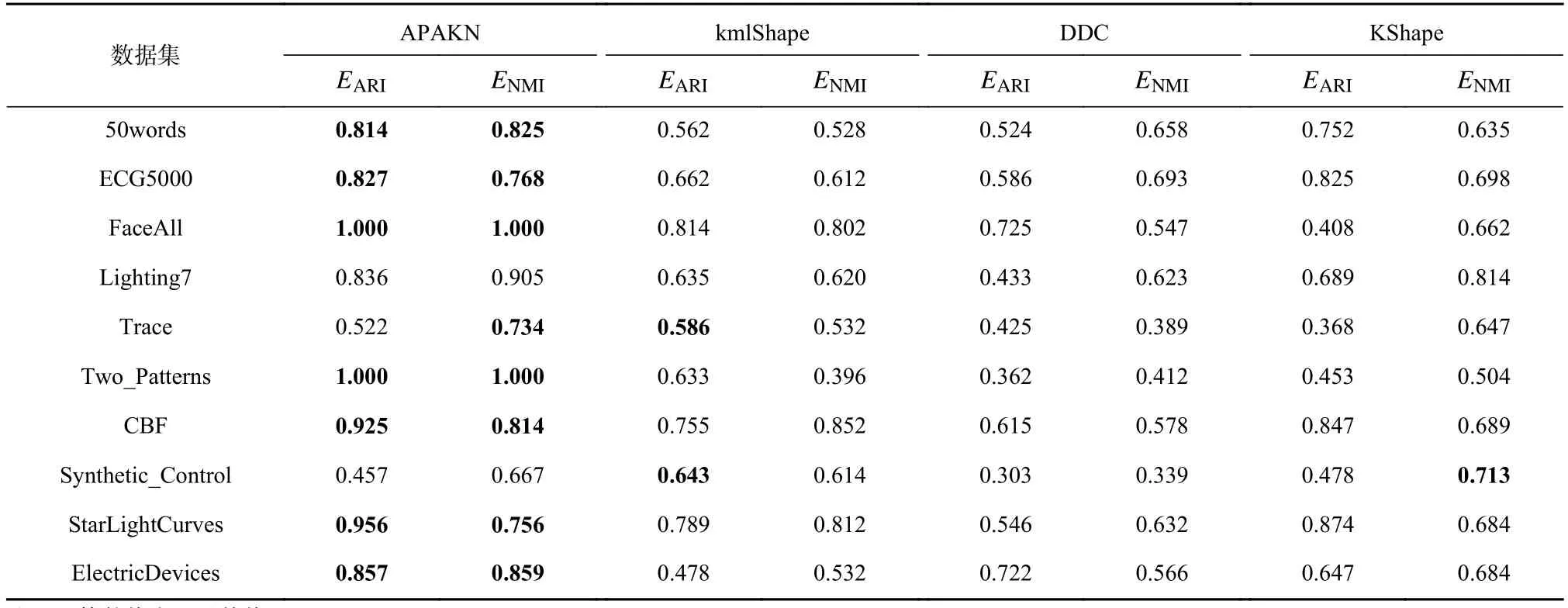
为了准确确定异常子序列,需要设置异常阈值T,将待检测子序列si(i=1,2,…,N)的异常分数S′(si)与异常阈值T相比较.若S′(si) 其中均值u和标准差 σ 是确定值,令参数 β∈{0,0.1,0.2,0.3,…,2.8,2.9,3.0}.为了选择合适的 β值确定最佳异常阈值T,以异常子序列和正常子序列的异常分数集合的方差之和作为目标函数,找出使得目标函数最小的 β以确定异常阈值T. 以图1中子序列为例确定异常阈值T:所有子序列的异常分数的均值和标准差分别为0.280和0.315,β∈{0,0.1,0.2,0.3,…,2.8,2.9,3.0},则 异 常 阈 值T∈{0.280,0.312,0.343,0.375,…,1.162,1.194,1.225}, 根 据这31个阈值取值分别得到31种异常子序列集合,根据式(12)计算得出目标函数值的集合,当 β =0.3 时取得目标函数的最小值0.015,此时确定异常阈值T=0.280+0.315×0.3=0.375,由于只有S′(s1)≥T,则检测出图1中子序列s1为异常子序. 针对异常子序列的多样性,为区分不同类型的异常子序列,本节对得到的异常子序列进行聚类,将每个聚类中心定义为一个异常模式,对不同的异常模式进行识别.本算法能够在聚类个数未知的情况下保证聚类结果的有效性. APAKN根据2个条件寻找聚类中心:1)聚类中心的密度高于其邻近的子序列的密度;2)任意2个类中心的距离相对较远.首先利用2.1节描述的自适应k近邻搜索算法确定所有异常子序列的自适应k近邻值(i=1,2,…,n),将其作为各异常子序列的密度.将异常子序列中自适应k值最大的子序列作为第1个聚类中心p1,在与p1距离最远的v个子序列中找出密度最大的异常子序列作为第2个聚类中心p2,其中即为异常子序列个数与10的比值取整加1.在距离存储单元搜索剩余子序列与2个聚类中心之间的距离,确定聚类数为2时各子序列所属聚类.同时使用轮廓系数 (silhouette coefficient)[29]作为聚类有效性指标计算当前的轮廓系数sil2. 当聚类数为q时,轮廓系数的计算公式为 其中N为所有子序列个数,Ci表 示第i个类簇,w为属于类簇Ci的 子序列,sam(w,Ci)被称为子序列w的簇内不相似度,是子序列w到同类其他子序列的平均距离,dif(w,Ci)被称为子序列w的簇间不相似度, 是子序列w到所有其他簇的所有子序列的平均距离中最小的那一个.定义分别为: 其中nCi为 类别Ci所 包含 子序列的 个数,nCl为 类 别Cl所包含子序列的个数,ddtw(w,u)表示子序列w与u之间的DTW距离.轮廓系数的值越大,说明同类样本相距越近,不同样本相距越远,聚类效果越好.使得有效性指标最大的聚类中心集合即是算法求得的所有聚类中心. 当聚类数为i时,在与已有聚类中心{p1,p2,…,pi−1}的距离之和最大的v个子序列中找出密度最大的异常子序列作为第i个聚类中心pi,把每个剩余异常子序列分配给距离其最近的聚类中心.计算此时的轮廓系数sili,若sili Fig.5 Schematic diagram of anomaly subsequence distribution图5 异常子序列分布示意图 算法 1.APAKN 算法. 输入:子序列数据集D={s1,s2,…,si,…,sN}; 输出:异常模式集合P={p1,p2,…,pi,…,pc}. 步骤1.对于数据集D={s1,s2,…,si,…,sN},计算所有子序列之间的DTW距离并将其存放在距离存储单元中以便随时调用,利用子序列距离搜索子序列si(i=1,2,…,N)的自适应k近邻值. 步骤2.将k值集合 {k1,k2,…,kN}中的最大值km代入式(6)计算所有子序列的相对密度,计算异常分数和确定异常阈值,将异常分数大于异常阈值的子序列检测为异常子序列 步骤3.重新搜索异常子序列s−的自适应k值j将其作为的密度,根据所得密度和距离存储单元中的子序列距离迭代地获取聚类中心,并根据式(13)中的轮廓系数判断迭代停止时聚类中心的个数c. 步骤4.输出聚类中心集合,即异常模式集合P={p1,p2,…,pi,…,pc}. APAKN算法采用DTW 度量所有子序列之间的距离,该步骤的最大时间复杂度为,其中数据集中子序列数为N, 所有子序列长度都为l;异常子序列检测步骤的最大时间复杂度为其中km为所有子序列自适应k值集合中的最大值;异常子序列聚类步骤的最大时间复杂度为,其中,n为异常子序列的个数.可见,APAKN算法的时间复杂度为由于NlogN++nlogn≪N2l2,算法的时间复杂度可以表示为 为了更好地验证所提出算法的有效性,采用了美国加州大学滨河分校 (University of California Riverside,UCR)的时间序列数据集合[30]中的10个通用数据集作为实验对象对本文算法进行实验评估.由于APAKN算法主要是由异常子序列检测和异常子序列聚类2个方面组成,因此实验部分也将从这2个方向来进行评价.实验环境均为 Win 10 64 b 操作系统,Python 3.7.6 软件,8 GB 内存,Intel(R) Core(TM),i5-4200H CPU@2.80 GHz 处理器. 本次实验所用数据为 10 个公开的UCR数据集,由于UCR数据集中并未标出各类子序列是否异常,所以我们选择子序列个数最多的一类作为正常类,随机选择其他几类中的若干子序列组成异常类,使各数据集的异常率不同.表3列出了本次实验中各数据集的详细信息.以50words数据集为例,原数据集包含50个类别,其中类别号为2的子序列簇包含最多的子序列且被选作正常类,类别号为4,10,43的子序列簇被选作异常类,从中随机选择若干子序列作为实验中的异常子序列. Table 3 Experimental Data Sets表3 实验数据集 3.2.1 评价指标 本节使用准确率(Accuracy)、精确率(Precision) 、召回率(Recall) 、F值作为性能评价指标来评价本算法中异常子序列检测部分的性能,分别定义为: 其中,TP被定义为将异常子序列检测为异常子序列的个数;FP为把非异常子序列检测为异常子序列的个数;FN为将异常子序列检测为非异常子序列的个数;TN表示将非异常子序列正确检测为非异常子序列的个数. 准确率代表的是所有正确预测的样本数占总样本数的比重;精确率衡量算法的查准率,即正确预测为异常子序列占全部预测为异常子序列的比例;召回率衡量算法的查全率,即正确预测为一场子序列占全部实际为异常子序列的比例;F值则为精确率和召回率的调和平均数,同时兼顾算法的精确率和召回率,F度量值的大小反映了聚类结果的精度,它是一个介于−1和1之间的值,该值越接近1,算法的精度就越高. 3.2.2 实验结果 为了证明APAKN算法的优异,图6将算法异常子序列检测部分在10个数据集上的部分实验结果可视化地表示出来.图6中共包含代表着10个数据集的10个子图,每个子图由2个部分组成:时间子序列和子序列异常分数.以50words数据集为例,该数据集的子序列长度为270,我们从类别号为4,10,43这3个异常子序列簇中分别选择了3个子序列,从类别号为2的正常子序列簇中选择若干子序列,将这些子序列的异常得分在图6 (a)中显示出来.如图6 (a)所示,异常子序列的异常分数远远高于正常子序列的异常分数.此外,对数据集的其他子序列都分配了一个异常分数来度量它们的异常程度. 为了验证提出的异常模式识别算法APAKN在异常子序列检测部分的性能, 本文比较了APAKN与DBAD[13],SFO[15],DLDE[18]算法在各数据集的实验结果.APAKN利用自适应k近邻搜索算法自动确定各子序列的最佳近邻值 {k1,k2,…,kN},km为近邻集合中的最大值;异常子序列检测部分的对比算法DBAD递归计算拟合分布均值方差,需要人为设置递归参数t;SFO需要人为设置近邻参数k;DLDE构造Hash表以加快估计子序列的局部密度,需人为设置参数Hash值h.为了突出显示本文算法的优越性能,在10个实验数据集上,对3个对比算法分别进行多次实验,最终选出一个使其对应检测结果最优的参数值作为其最佳参数,分别记为topt,kopt,hopt.APAKN算法得到的自适应k值中的最大值km以及对比算法相应的topt,kopt,hopt如表4所示. Fig.6 UCR partial time subsequences and anomaly scores图6 UCR部分时间子序列及其异常得分 此外,APAKN提出基于最小方差的自适应阈值方法确定异常阈值;SFO算法利用统计假设检验方法判断数据是否异常,其计算较为复杂;而DLDE算法只是对所有数据对象按异常分数值降序排序,人为选择异常分数值最大的几个数据对象作为异常对象,该阈值选择方法需要实验者熟悉各数据集,并且对不同数据集进行实验时需要置换阈值参数,使实验过程更为繁琐.DBAD利用均值和方差确定异常阈值,同样需要人为设置阈值参数.本次实验利用较为常见的 3 σ准则作为DBAD和DLDE算法的异常阈值T=u+3σ.基于表4的最佳参数,表5和表6分别给出了4种算法在异常子序列检测部分的精确率和召回率以及准确率和F值. 表5给出了4种算法在10个数据集上异常子序列检测的精确率和召回率对比,表6则给出了异常子序列检测部分的准确率和F值对比, 可以看出,APAKN在10个数据集上的实验结果皆具有最佳性能.此外,DBAD算法有1个最佳精确率和1个最佳召回率;SFO有6个最佳召回率;DLDE有4个最佳精确率.由上述实验结果可以判断出,相较于其他算法,本文算法不仅具有很强的自适应性,而且具有很高的异常子序列检测水平. Table 4 km Value of APAKN and the Optimal Parameter Values of Comparison Algorithms表4 APAKN的 km 值和对比算法的最佳参数值 3.3.1 评价指标 本文利用调整兰德系数 (adjusted rand index, ARI)[31]和标准化互信息 (normalized mutual information, NMI)[32]两种衡量标准对异常子序列聚类结果进行评判.这2个衡量标准的上限均为1,该值越接近1,表示该聚类算法的准确率越高,算法聚类结果越好. Table 5 Comparison of Accuracy and Recall of Each Algorithm on 10 Data Sets表5 各算法在 10 个数据集上的精确率和召回率对比 Table 6 Comparison of Accuracy and F Value of Each Algorithm on 10 Data Sets表6 各算法在 10 个数据集上的准确率和F值对比 调整兰德系数值EARI定义为 其中na表示在算法聚类结果中为同一类、在数据集真实聚类中也为同一类的子序列对数;nb表示在算法聚类结果中为同一类、在数据集真实聚类中不为同一类的子序列对数;nc表示在算法聚类结果中不为同一类、在数据集真实聚类中为同一类的子序列对数;nd表示在算法聚类结果中不为同一类、在数据集真实聚类中也不为同一类的子序列对数. 标准化互信息值ENMI定义为 其中cA表 示算法聚类结果的聚类类别数,cB表示数据集本质聚类类别数,nij表 示子序列属于真实标签类j但被划分到聚类结果簇i中的个数,ni表示聚类结果类i中子序列的个数,nj表示真实标签类j中子序列的个数. 3.3.2 实验结果 为了证明APAKN算法的优异, 图7和图8分别将算法异常子序列聚类部分在50words和CBF数据集上的实验结果可视化地表示出来.图7包含代表着3类异常子序列的异常子序列示例和聚类算法下生成的簇质心即异常模式.通过图7中不同类别下的异常子序列的示例可以看出,同一类别下的异常子序列具有相同的趋势.从异常模式图可以看出算法得到的质心很好地表征了每个类别的趋势特征. 在异常子序列聚类部分,本文选择了kmlShape[21],DDC[23],KShape[24]算法进行性能比较.APAKN的聚类部分同样无需设置任何参数,而为了更好地显示出算法的优异性,对3种对比算法都进行了参数调优.由于kmlShape算法选取的初始类簇中心不同,则聚类结果也不同,对每个数据集进行多次重复实验, 取其中最好的结果.kmlShape,DDC,KShape算法需要给定类簇个数,为这3种算法分别选出一个使评价指标最优的参数作为其聚类个数.表7为APAKN的异常子序列聚类部分在10个UCR数据集上与kmlShape,DDC,KShape这3种算法的聚类结果对比. 通过表7可知,即使已经给定了对比算法的最佳参数,kmlShape,DDC,KShape算法的聚类结果还是波动较大, DDC聚类效果不佳.kmlShape算法在FaceAll,Trace,CBF,Synthetic_Control数据集上的性能值较优,在其他数据集上的表现不佳;KShape算法在 50words,ECG5000,Lighting7,CBF 数据集上表现较好.但从总体上来看,APAKN在各个数据集上的评价指标值大部分都要优于与之比较的算法,其余指标均值与最佳指标值相差不大. Fig.7 Examples of anomaly subsequences and anomaly patterns in different categories of the 50words dataset图7 50words数据集在不同类别下的异常子序列示例和异常模式 Fig.8 Examples of anomaly subsequences and anomaly patterns in different categories of the CBF dataset图8 CBF数据集在不同类别下的异常子序列示例和异常模式 Table 7 Comparison of ARI and NMI of Each Algorithm on 10 Data Sets表7 各算法在 10 个数据集上的ARI和NMI对比 因此,结合异常子序列检测与异常子序列聚类2部分的实验结果, 可以验证出算法APAKN是有效可行的. 本文提出了基于自适应k近邻的异常模式识别算法APAKN,该算法在无需任何参数输入的情况下,不仅检测异常子序列,还区分出异常子序列的不同类别,重新定义了异常模式.采用自适应k近邻搜索算法获取子序列的自适应k近邻值,解决传统k近邻算法的参数设置问题;提出一种基于最小方差的自适应阈值方法解决阈值选择问题;APAKN通过密度与距离结合的思想寻找最优聚类中心,并利用轮廓系数得到聚类数,从而实现异常子序列的快速聚类.在UCR数据集上的实验结果表明了APAKN算法的自适应性与有效性.下一阶段我们将考虑如何从距离度量方面减少算法的时间复杂度以期望提高算法的效率. 作者贡献声明:王玲提出文章的算法思路设计,对论文的逻辑性以及算法的合理性进行指导;周南负责文章的定理和论证过程,以及实验部分的算法实现与实验结果分析;申鹏对文章整体格式进行修改.
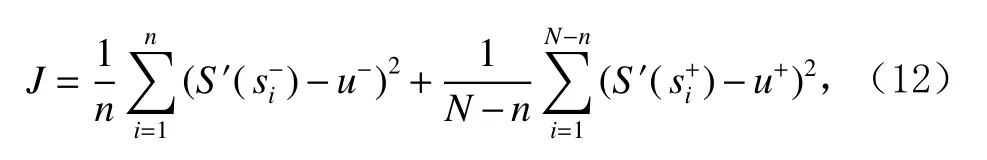
2.2 基于自适应 k 近邻的异常子序列聚类
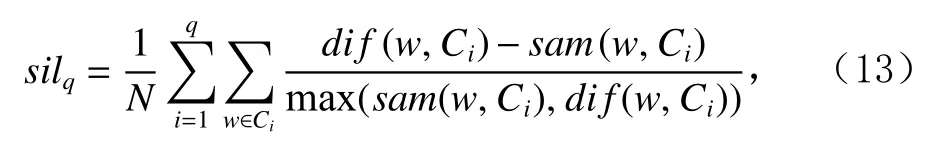
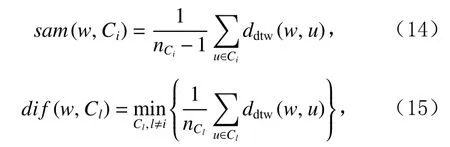
2.3 APAKN算法步骤
2.4 时间复杂度
3 实验与结果
3.1 实验数据
3.2 异常子序列检测
3.3 异常子序列聚类
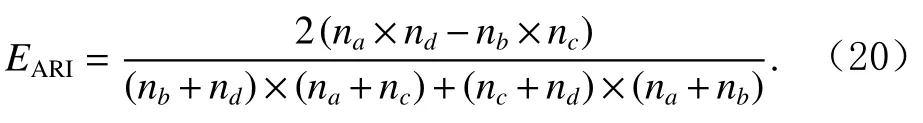
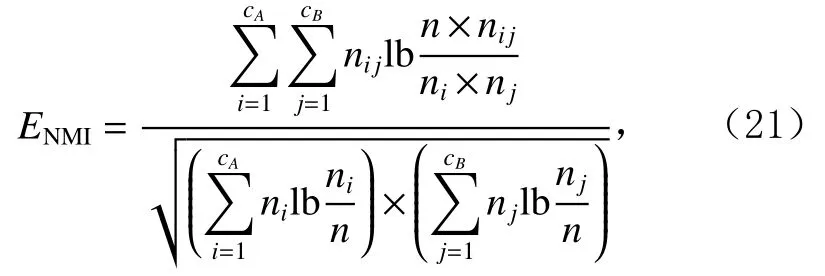
4 结 论

