因果机器学习的前沿进展综述

李家宁 熊睿彬 兰艳艳 庞 亮 郭嘉丰 程学旗

1 （中国科学院网络数据科学与技术重点实验室（中国科学院计算技术研究所） 北京 100190）

2 （中国科学院大学 北京 100049）

3 （清华大学智能产业研究院 北京 100086）

4 （中国科学院计算技术研究所数据智能系统研究中心 北京 100190） （lijianing@ict.ac.cn）

机器学习是一门研究如何设计算法、利用数据使机器在特定任务上取得更优表现的学科，其中以深度学习[1]为代表的相关技术已成为人们研究实现人工智能方法的重要手段之一.至今机器学习研究已经取得大量令人瞩目的成就：在图像分类任务上的识别准确率超过人类水平[2]；能够生成人类无法轻易识别的逼真图像[3]和文本[4]；在围棋项目中击败人类顶尖棋手[5]；蛋白质结构预测结果媲美真实实验结果[6]等.目前机器学习在计算机视觉、自然语言处理、搜索引擎与推荐系统等领域发挥着不可替代的作用，相关应用涉及互联网、安防、医疗、交通和金融等众多行业，对社会发展起到了有力的促进作用.

尽管机器学习研究获得了一系列丰硕的成果，其自身的问题却随着应用需求的提高而日益凸显.机器学习模型往往在给出预测结果的同时不会解释其中的理由，以至于其行为难以被人理解[7]；同时机器学习模型还十分脆弱，在输入数据受到扰动时可能完全改变其预测结果，即使这些扰动在人看来是难以察觉的[8]；机器学习模型还容易产生歧视行为，对不同性别或种族的人群给予不同的预测倾向，即使这些敏感特征不应当成为决策的原因[9].这些问题严重限制了机器学习在实际应用中发挥进一步的作用.

造成这一系列问题的一个关键原因是对因果关系的忽视.因果关系，指的是2个事物之间，改变一者将会影响另一者的关系.然而其与相关关系有所不同，即使2个事物之间存在相关关系，也未必意味着它们之间存在因果关系.例如图像中草地与牛由于常在一起出现而存在正相关关系，然而两者之间却没有必然的因果关系，单纯将草地改为沙地并不会改变图像中物体为牛的本质.机器学习的问题在于其模型的训练过程仅仅是在建模输入与输出变量之间的相关关系，例如一个识别图像中物体类别的机器学习模型容易将沙地上的牛识别为骆驼，是因为训练数据中的牛一般出现在草地上而沙地上更常见的是骆驼.这种具备统计意义上的相关性却不符合客观的因果规律的情况也被称为伪相关（spurious correlation）.伪相关问题的存在对只考虑相关性的机器学习模型带来了灾难性的影响：利用伪相关特征进行推断的过程与人的理解不相符，引发可解释性问题；在伪相关特征发生变化时模型预测结果会随之改变从而导致预测错误，引发可迁移性和鲁棒性问题；如果伪相关特征恰好是性别和肤色等敏感特征，则模型决策还会受到敏感特征的影响，引发公平性问题.忽视因果关系导致的这些问题限制了机器学习在高风险领域及各类社会决策中的应用.图灵奖得主Bengio指出，除非机器学习能够超越模式识别并对因果有更多的认识，否则无法发挥全部的潜力，也不会带来真正的人工智能革命.因此，因果关系的建模对机器学习是必要的，需求也是十分迫切的.

因果理论即是描述、判别和度量因果关系的理论，由统计学发展而来.长期以来，由于缺乏描述因果关系的数学语言，因果理论在统计学中的发展十分缓慢.直到20世纪末因果模型被提出后，相关研究才开始蓬勃兴起，为自然科学和社会科学领域提供了重要的数据分析手段，同时也使得在机器学习中应用因果相关的技术和思想成为可能.图灵奖得主Pearl将这一发展历程称为“因果革命”[10]，并列举了因果革命将为机器学习带来的7个方面的帮助[11].本文将在机器学习中引入因果技术和思想的研究方向称为因果机器学习（causal machine learning）.目前机器学习领域正处于因果革命的起步阶段，研究者们逐渐认识到了因果关系建模的必要性和紧迫性，而因果机器学习的跨领域交叉特点却限制了其自身的前进步伐.本文希望通过对因果理论和因果机器学习前沿进展的介绍，为相关研究者扫清障碍，促进因果机器学习方向的快速发展.目前针对因果本身的研究已有相关综述文献[12−14]，内容主要涵盖因果发现和因果效应估计的相关方法，但很少涉及在机器学习任务上的应用.综述文献[15−16]详细地介绍了因果理论对机器学习发展的指导作用，着重阐述现有机器学习方法的缺陷和因果理论将如何发挥作用，但缺少对这一方向最前沿工作进展的整理和介绍，而这正是本文重点介绍的内容.

1 因果理论简介

因果理论发展至今已成为统计学中的一个重要分支，具有独有的概念、描述语言和方法体系.对于因果关系的理解也已经不再仅停留在哲学概念的层面，而是有着明确的数学语言表述和清晰的判定准则.当前广泛被认可和使用的因果模型有2种：潜在结果框架（potential outcome framework）和结构因果模型（structural causal model, SCM）.Splawa-Neyman 等人[17]和Rubin[18]提出的潜在结果框架又被称为鲁宾因果模型（Rubin causal model, RCM），主要研究 2 个变量的平均因果效应问题；Pearl[19]提出的结构因果模型使用图结构建模一组变量关系，除了效应估计也会关注结构发现问题.RCM与SCM对因果的理解一致，均描述为改变一个变量是否能够影响另一个变量，这也是本文所考虑的因果范畴.两者的主要区别在于表述方法不同，RCM更加简洁直白，相关研究更为丰富；而SCM表达能力更强，更擅长描述复杂的问题.虽然目前依然存在对因果的其他不同理解，这些理解通常不被视为真正的因果，例如格兰杰因果（Granger causality）[20]描述的是引入一个变量是否对另一个变量的预测有促进作用，本质上仍是一种相关关系.

本节将对因果相关概念以及RCM与SCM 的相关理论和技术进行简要介绍.由于本文关注的主要内容是因果机器学习而不是因果本身，本节将侧重于介绍机器学习中所使用的因果的概念和思想，而不会过多关注因果领域自身的前沿研究.

1.1 因果概念

统计学中对于因果关系的定义符合人们直觉上的认知.在一个数据系统中，用于分析的数据通常会表述为一组变量，每个变量都对应一种已知或未知的产生机制.对于2个给定的变量，如果在保持其他机制不变的情况下，改变一个变量会使得另一个变量也发生改变，则称前者为因，后者为果，同时称两者之间存在因果关系（causal relationship），因变量对果变量的影响称为因果效应（causal effect）.求解 1 对或多对变量是否存在因果关系以及因果效应强度的任务称为因果推断（causal inference）.通常而言，如果对因果效应强度的定量研究是显著的，则认为因果关系存在.判定因果关系的存在性将不可避免地涉及到对原始变量系统的改变，即需要改变目标变量的产生机制，这也是其区别于相关关系（correlation）的关键点.相对而言，判定2个变量X和Y是否存在相关关系则不需要改变系统，只需检验观测变量的边际分布与条件分布是否一致，即判定P(X|Y)=P(X)是否成立.Pearl等人[10]在阐述相关和因果之间的差异时提出了“因果之梯（ladder of causation）”的概念，自下而上将问题划分为关联、干预和反事实3个层次，分别对应于观察、行动和想象3类活动.通常而言，回答因果问题需要借助反事实或者干预，若希望仅借助关联来判定因果关系则必须处理好混杂因素，这些都是研究因果理论所需的重要概念.下面将从回答因果关系判定问题的角度出发，对反事实、干预和混杂因素3个概念进行介绍.

反事实（counterfactual）指的是在已经观测到一组变量的情况下，假设其中部分变量具有另外的取值的操作.例如人在反思自己的行为时，往往会考虑“如果我当时没有做某事而是做了其他某事，那么结果将会怎样”，这是典型的基于反事实的思考，是根据结果溯源寻找原因的有效手段.如果发现某个变量改变取值后会导致结果改变，该变量即是结果的原因之一.反事实考虑的是一种实际并未发生过也难以再次观测到的情景，因为它假定2次观测之间除了需要研究的变量有所改变外，其他外部变量取值和作用机制需完全保持一致.尽管反事实操作的结果直接反映了变量之间的因果关系，由于通常无法针对同一个体平行地实施2种不同操作，使得在实际应用中几乎无法用于因果判定，更多情况下只是作为一种指导性思想使用.想要判断因果关系的存在性，人们只能诉诸群体层面上的平均观测结果，即采用干预操作.

干预（intervention）指的是改变部分变量产生机制并维持其余机制不变的操作，是因果关系判定和度量的关键操作.如果对一个变量的干预改变了另一个变量的概率分布，则意味着前者是后者的因.例如，通常认为海拔高度是气温的因，这是因为海拔高度通过特定的物理机制对气温产生了影响.如果对海拔高度进行干预，即调整地理位置来改变海拔，气温也会随之产生变化，因为背后的物理机制仍然能够生效；相反，如果对气温进行干预，例如提供额外的热源对空气进行加热，这改变了气温的产生机制却保持海拔的产生机制不变，最终海拔并不会因此而改变.可见通过干预操作可以对因果关系的存在性和方向性做出清晰的判断，事实上这也是科学研究中最常用的手段，随机对照实验即属于这一思路.干预不同于反事实，不要求外部变量的取值严格一致，只需要满足概率分布不变的假设即可，这在一般的应用场景中通常可以满足，因此更常用于因果关系的判定.然而这种通过干预观测系统的改变来判断因果关系的做法并不能解决实际中所有的因果问题，在许多情况下干预操作的成本过高或实施风险过大，甚至可能因为违反伦理道德而无法实际实施，如研究吸烟对肺癌的影响时不能强制要求普通人群吸烟.这种情况下就需要避免对目标变量进行干预，而仅仅通过观测原有机制产生的数据来估计干预的效果，这类研究问题也成为了因果推断领域重点关注的问题.

混杂因素（confounder）指的是一类变量，如果不对它们的取值进行控制，通过观测数据得到的干预结果的估计就会产生偏差.通常来说，混杂因素指的是那些能够对所研究的一对变量同时产生影响的因素.例如对于儿童穿鞋尺码与阅读能力呈正相关的现象，年龄即是一个混杂因素，如果不控制年龄则会得出“儿童穿更大尺码的鞋子能提升其阅读能力”的错误结论，相反若控制年龄变量，即针对不同年龄的儿童分组考察他们鞋子尺码与阅读能力的关系，则会发现两者之间不存在相关关系.理论上如果可以发现并控制所有的混杂因素，那么因果关系的判定就等价于该条件下相关性的判定.然而寻找一个充分的变量集合以囊括所有的混杂因素是十分困难的，也不可能在不做任何假设的情况下判断已有变量集合是否充分.另外，简单地将所有其他变量都视为混杂因素的做法也不可取，例如研究一个人才华和外貌的关系时，对其是否是名人这一变量进行控制就是错误的.因为一个人成名需要好的才华或者好的外貌，两者都不好的人很难成为名人，所以如果一个名人的外貌不好那么他就更可能有好的才华.在这种受控条件下两者呈现一种负相关，即使原本两者是不相关的.如何鉴别和处理混杂因素始终是因果推断领域的核心问题之一.

1.2 因果模型

记待研究的变量为X和Y，其他协变量（covariate）构成的向量为Z=(Z1,Z2,···).为简化考虑，假设X是二值{变量，即取}值只能为 0或 1.现在观测到1组数据D=X(i),Y(i),Z(i)ni=1，需要估计X取值由 0变为 1时对Y的因果效应.由于Z中可能存在混杂因素，直接使用条件期望差值 E [Y|X=1]−E[Y|X=0]作为估计值可能导致偏差.在这种情况下想要准确进行因果效应估计，需要做出适当的假设构建模型.本节将对RCM 和SCM这2种因果模型的概念理论内容进行简要介绍.

1.2.1 潜在结果框架(RCM)

潜在结果指的是一个个体如果接受了某种处理会怎样，也就是指如果X(i)取某种值时对应Y(i)取值会如何.对于个体i来说，采取X=x的处理的潜在结果记作Yx(i)，X(i)对Y(i)带来的因果效应可由X(i)的不同取值对应的潜在结果差值来计算，即个体处理效应（individual treatment effect, ITE）， 定 义 为ITE(i)=Y1(i)−Y0(i).由于同一个个体通常不可能既采取X=0的处理同时也采取X=1的处理，实际最多只能观测到1个结果，另一个结果则是反事实的，这也是被称为“潜在结果”的原因.X对Y的总体因果效应记为个体处理效应的期望，称为平均处理效应（average treatment effect, ATE）：

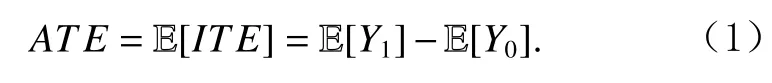
平均处理效应等同于对X的不同干预所得结果之差.如果这种干预是实际可行的，那么可以直接通过干预操作获得潜在结果的平均取值，从而计算ATE.干预意味着X的取值不再由观测决定，而是由实验者确定，这种方式通常称为随机对照实验，X=1的群体称为处理组，X=0的群体称为控制组.

然而如1.1节所述，干预在许多情况下是不可行的，只能使用观测数据对ATE进行估计.基于潜在结果框架使用观测数据研究因果效应的做法最早由Rubin[18]提出，因此该模型也称作鲁宾因果模型，即RCM.RCM对因果的描述较为简洁，除了要研究因果效应的一对变量以外，对其他变量的相互作用机制不做假设，因此经常在进行因果效应估计的场景中使用.这种情况下需要考虑混杂因素，真实的ATE 可以由通过控制全部混杂因素获得.对变量进行控制指的是按照该变量的不同取值分组，组内计算效应期望之后再在组间计算期望.如果Z包含了全部混杂因素，那么

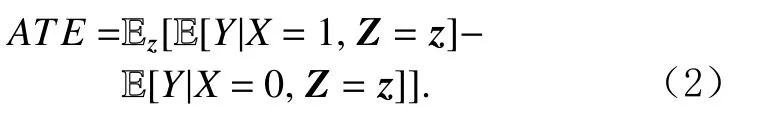
在RCM中，如果满足一定的假设，上述计算得到的ATE即是X对Y的真实因果效应.这些假设包括：

1)个体处理值稳定假设（stable unit treatment value assumption, SUTVA）[21]，指的是一个个体的潜在结果不受其他个体处理的影响.例如一个人服用药物获得的治疗效果不受其他人是否服用药物的影响.

2)处 理 分 配 机 制 可 忽 略 性 （ignorability of treatment assignment mechanism）[22]，指的是固定混杂因素后，潜在结果不受处理方式的影响.例如对于一个人是否服药导致的潜在治疗效果具有确定性，不随实际是否服药的行为而发生改变.

3)正值性（positivity）[22],指的是对于每个个体均有非零的可能性采取每种处理方式.

采用控制所有混杂因素的方法计算ATE在实际问题中可能会遇到困难，通常是由于混杂因素的维度很高，控制相同取值的样本可能数量很少，导致期望估计不准确.针对这一问题，研究者们提出了多种解决方案.常见的方法有基于倾向性得分的估计方法、基于回归的估计方法以及两者相结合的方法.倾向性得分（propensity score）指的是给定协变量Z的情况下获得处理X=1的概率，即P(X=1|Z)，可以使用机器学习模型进行建模.文献[22]指出，在ATE的表达式中使用倾向性得分代替协变量Z仍能够保证估计的正确性，因此可以通过控制倾向性得分计算分组期望的方式来计算ATE.一种做法称为倾向性得分匹配（propensity score matching）[22]，为处理组中的每个个体选择得分最接近的1个或1组对照组个体进行匹配，计算它们结果的平均差值，然后在整个处理组上取平均，即可得到ATE的估计.另一种做法称为逆处理概率加权（inverse probability of treatment weighting,IPTW）[23]，也称为IPW或IPS，通过将每个样本的结果除以倾向性得分后再取平均，即可得到ATE的估计值IPTW:

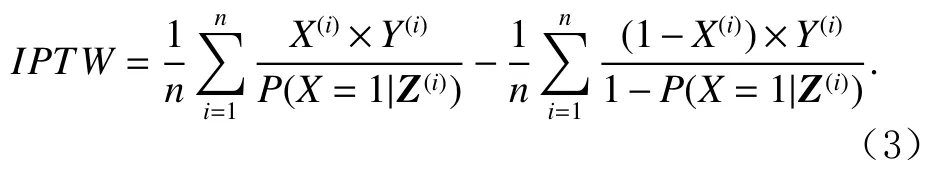
基于回归的估计方法简称回归估计[24]，其思想是使用机器学习模型建模给定处理X和协变量Z时结果Y的期望，即 E [Y|X,Z]，然后用这一回归模型来模拟干预，即可得到ATE的估计值REG：

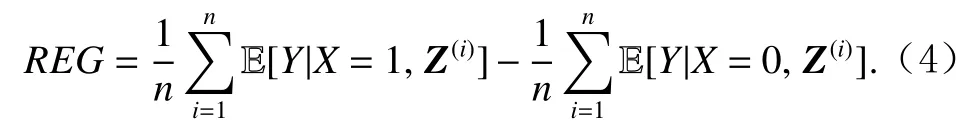
回归估计方法可以和IPTW方法相结合得到双稳健估计（doubly robust estimation, DRE）[25]：只要2种估计中的1种是可靠的，那么DRE整体即是可靠的.

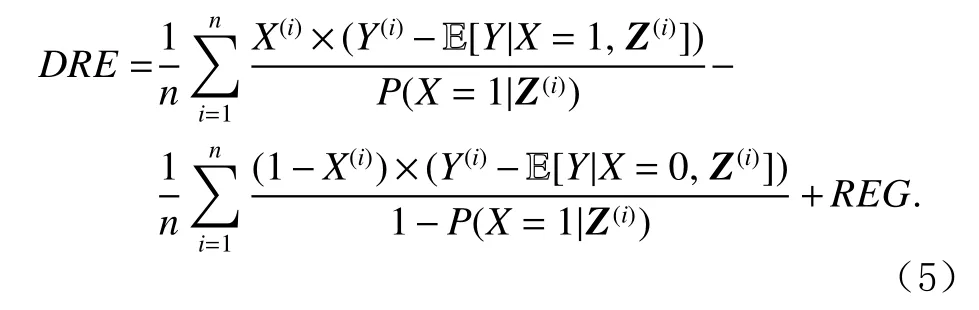
除以上方法外，还有混杂平衡（confounder balancing）[26]、分层（stratification）[27]等众多其他方法处理混杂因素的问题，可参考文献[28]中的介绍，在此不再详细展开.这些方法都要求混杂因素的值是可观测的，限制了RCM在一些场景中的应用.这种情况下的部分问题可以使用SCM解决.

1.2.2 结构因果模型(SCM)

SCM由Pearl[19]提出，其思想是将所有需要考虑的变量组织成一个有向无环图，图的每个节点都代表1个变量，1条由节点A指 向节点B的有向连边代表A对B有直接的因果作用.这种图又称为因果图（causal graph），记作G=(V,E)，其中节点集合V={X,Y,Z1,Z2,···}包含所有考虑的变量，边集合E包含所有对变量直接因果关系的先验假设.例如儿童穿鞋尺码与阅读能力关系的因果图可如图1(a)表示（假设穿鞋尺码对阅读能力的因果效应是待研究的未知量）：

结构因果模型中的一个重要概念是结构方程（structural equations），其假设每个节点都对应一个未观测到的外生变量（exogenous variable），节点的值由该外生变量及所有直接父节点变量通过一个方程来唯一确定，例如

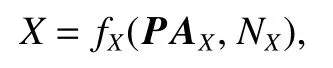
其中PAX指的是节点X的所有父节点变量，NX是X对应的外生变量.图1所对应的完整结构方程为

之所以称为这些方程是“结构方程”，是因为其代表变量的生成机制，只能由等式右边对左边赋值，而不能随意变换方向.外生变量描述的是对应节点变量的所有随机因素，其自身具有确定性的概率分布，通常未被观测也无法进行控制，而且SCM中假设所有外生变量之间相互独立，图1(b)展示了一个外生变量的例子.通过结构方程和外生变量，SCM能够很清晰地定义干预和反事实操作，其中干预操作是将干预节点的结构方程替换掉，对应在因果图中即是去掉所有指向干预节点的箭头.这在SCM中也称为do操作，例如将通过干预将节点X的取值置为 1记作do(X=1)，X的结构方程也对应修改为X=1，意味着X不再受其父节点和外生变量的影响.反事实操作同样由do操作给出，但同时会限制所有外生变量取值不变.

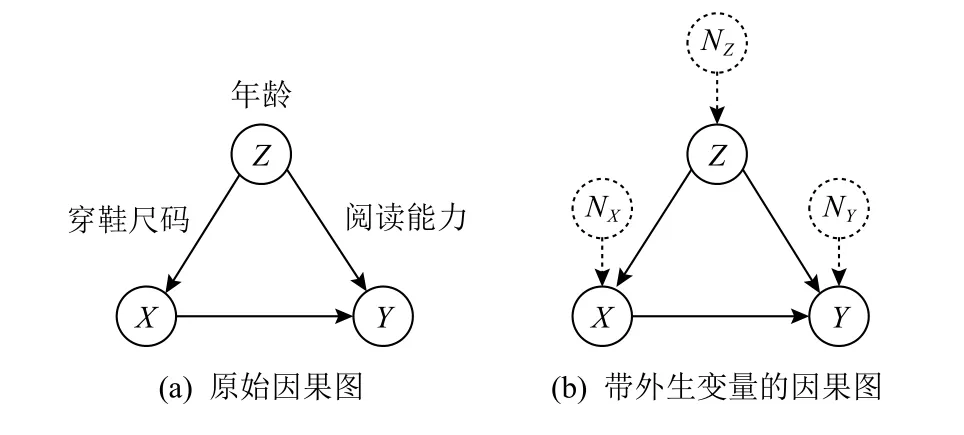
Fig.1 Example of causal graph图1 因果图示例

在SCM中，混杂因素识别可以直接借助因果图结构完成，一个变量成为混杂因素当且仅当存在由该节点指向X和Y的各1条有向路径（指向Y的路径不能通过X）.X对Y的因果效应仍然可以像RCM 中一样在识别混杂因素后计算ATE得到，不过在SCM中可以由干预操作直接给出，即E[Y|do(X=1)]−E[Y|do(X=0)].这种方法的关键是计算P(Y|do(X=x))，这可以通过将因果图视为贝叶斯网络（Bayesian network）进行概率分解得到.然而由do操作定义直接给出的求解方法面对稍复杂的因果图时也会变得很复杂，因此一般不会直接使用.更常用的方法称为后门调整（backdoor adjustment）：一条指向X并连接Y的路径称为X到Y的后门路径，通过控制路径上的某些节点使得所有后门路径被关闭的方法称为后门调整.路径上的边均指向自身的节点称为对撞节点（collider）.一条路径是关闭的，当且仅当某个对撞节点没有被控制或者某个非对撞节点被控制.RCM中控制所有混杂因素而不控制其他节点的做法恰恰是后门调整中的一个特例.例如图2(a)中的因果图，Z是一个混杂因素，X←W←Z→Y是一条后门路径，W和Z均不是对撞节点，所以单独控制Z或W，或者同时控制两者都是可以的.

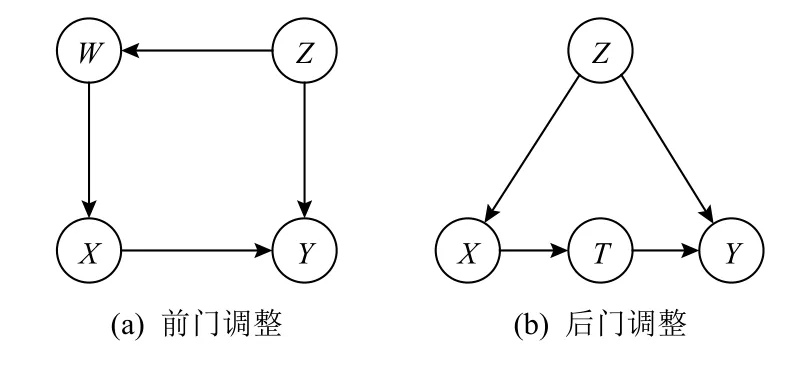
Fig.2 Example of frontdoor/backdoor adjustment图2 前门/后门调整示例

使用SCM相对于RCM的优势最主要体现在混杂因素无法观测的场景.这种情形下RCM将无法使用，而SCM 可以通过一种称为do演算（do-calculus）的方法将因果效应的计算转化为仅在可观测变量上的计算，从而解决部分问题.do演算包含3条规则，这些规则已被证明是完备的，即如果存在一种仅通过可观测变量的观测分布计算因果效应的方法，那么这种方法一定能由do演算推导得到，由于篇幅所限不在此展开详细介绍.do演算的一个常见实例是前门调整（frontdoor adjustment）[29]，如图2(b)中的因果图，变量T称为前门变量，因为其不受Z的直接影响，且X对Y的效应仅仅通过T生效.通过前门变量T可以在不观测Z的情况下计算因果效应：

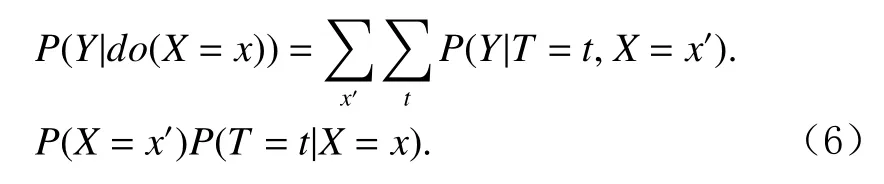
在因果推断及因果机器学习任务中，因果图通常是未知的.一种方式是根据具体问题结合领域知识给出先验的因果图结构，另一种方式是从数据中学习部分因果图信息.后者又被称为因果发现（casual discovery）任务，目的是从一系列变量的观测结果中推断因果图结构.因果发现有3类主要方法：基于约束的方法、基于评分的方法和基于结构方程的方法.基于约束的方法主要考虑数据中的条件独立性，通过检验各个变量之间是否条件独立，给出可能的因果图的等价类，即确定部分连边及其方向.这类方法包括 PC（Peter and Clark）[30]，IC（inductive causation）[31]，FCI（fast causal inference）[32]方法等.基于评分的方法思路是利用评分函数来求解得分最高的因果图，常见的评分为贝叶斯信息准则（Bayesian information criterion, BIC）[33]，即联合考虑样本似然和因果图的复杂度，代表性方法是 GES（greedy equivalence search）[34].基于结构方程的方法是对结构方程的形式做一定的假设，从而可以求解完整的因果图，但同时适用范围也受到方程形式的限制，常见方法包括LiNGAM（linear non-Gaussian acyclic model）[35]和后非线性模型（post-nonlinear model）[36]等.因果发现在实际应用中面临的最大问题是可识别性（identifiability），即能否从观测数据中识别唯一确定的因果图.

因果图的出现还催生了中介分析[37-38]的研究方向，即在有中介变量（mediator）存在的情况下将X对Y的因果效应分解为直接效应和间接效应.如图3所示，X对Y产生的因果效应由2条路径共同决定，一条是经由中介变量M间接影响Y，一条是直接对Y产生影响.

假设已观测到X=x,M=m时有Y=Yxm，这一观测相对于参考情况X=x∗下的期望Y=E[Yx∗]之间的差距称为全效应（total effect, TE），即TE=Yxm− E[Yx∗].直接效应和间接效应需要依靠反事实来定义，例如直接效应可以视为在观测样本上缺少X=x造成的差距或者在参考情况下添加X=x造成的差距，前者称为全直接效应（total direct effect, TDE），后者称为自然直 接 效 应（natural direct effect, NDE）， 分 别 有TDE=Yxm−Yx∗m，NDE=E[Yx]−E[Yx∗].同样地，间接效应也分为 2 种，全间接效应（total indirect effect, TIE）与自然间 接 效 应（natural indirect effect, NIE）， 分 别 有TIE=Yxm−E[Yx]，NIE=Yx∗m− E[Yx∗].以上效应之间满足关系TE=TDE+NIE=TIE+NDE.

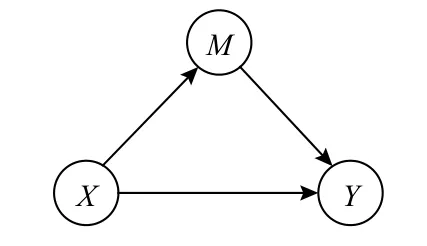
Fig.3 Example of mediation analysis图3 中介分析示例

2 因果机器学习相关工作介绍

近年来随着因果理论和技术的成熟，机器学习领域开始借助因果相关技术和思想解决自身的问题，这一研究方向逐渐受到研究者越来越多的关注.至今，因果问题被认为是机器学习领域亟待解决的重要问题，已成为当下研究的前沿热点之一.机器学习可以从因果技术和思想中获得多个方面的益处.首先，因果理论是一种针对数据中规律的普适分析工具，借助因果图等语言可以对研究的问题做出细致的分析，有利于对机器学习模型的目标进行形式化以及对问题假设的表述.其次，因果推断提供了消除混杂因素以及进行中介分析的手段，对于机器学习任务中需要准确评估因果效应及区分直接与间接效应的场景有十分重要的应用价值.再者，反事实作为因果中的重要概念，也是人在思考求解问题时的常用手段，对于机器学习模型的构建和问题的分析求解有一定的指导意义.

本节将对近年来因果机器学习的相关工作进行整理介绍，涉及应用领域包括计算机视觉、自然语言处理、搜索引擎和推荐系统等.按照所解决问题的类型进行划分，因果机器学习主要包括以下内容：可解释性问题主要研究如何对已有机器学习模型的运作机制进行解释；可迁移性问题主要研究如何将模型在特定训练数据上学到的规律迁移到新的特定环境；鲁棒性问题主要研究寻找普适存在的规律使模型能够应对各种未知的环境；公平性问题主要研究公平性度量指标并设计算法避免歧视；反事实评估问题主要研究如何在存在数据缺失的场景中进行反事实学习.这些问题与因果理论的关系如图4所示，下面针对这些问题分别展开介绍.

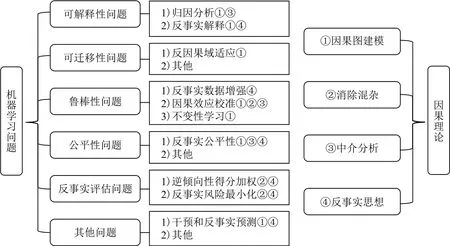
Fig.4 Overview of main research problems in causal machine learning图4 因果机器学习的主要研究问题总览

2.1 可解释性问题

机器学习模型会根据给定输入计算得到对应的输出，但一般不会给出关于“为什么会得到此输出”的解释.然而这种解释有助于人们理解模型的运作机制，合理的解释能够使结果更具有说服力.因此近年来涌现出许多致力于为现有模型提供解释方法的工作，为模型的诊断分析提供了有效手段[39].解释的核心在于“模型得到此输出，是因为输入具有什么样的特征”，这本质上是在探讨在此模型参与过程中输入特征与输出结果之间的因果关系，例如估计特征对输出变量的因果效应强度.

由于机器学习模型对输入数据的处理过程是一个独立而完整的过程，输入与输出变量之间一般不会受到混杂因素的影响，因此即使不使用因果术语也可以对任务进行描述.这体现为早期的模型解释方法并不强调因果，少数强调因果的方法也并不一定依赖因果术语.因果理论的引入为可解释性问题领域带来的贡献主要有2个方面：一是在基于归因分析的解释方法中建模特征内部的因果关系；二是引入一类新的解释方法即基于反事实的解释.基于归因分析和基于反事实的解释构成了当前最主要的2大类模型解释方法如表1所示，以下分别展开介绍.

2.1.1 基于归因分析的解释方法

基于归因分析（attribution）的方法是机器学习模型解释方法中最早出现也是最为成熟的方法.对于一个具有n个特征的样本X=(X1,X2,···,Xn)，模型将其映射为输出Y=y，归因分析指的是为每个特征分配一个 归因 值，即构造一个归因向量Φ =(ϕ1,ϕ2,···,ϕn)， 其 中 ϕi代 表 特 征Xi=xi对 结 果Y=y的 贡 献 大 小（本节所用符号与前文无关）.基于归因分析的常见解释 方 法 主 要 包 括 ：LIME[40]， Grad-CAM[41]， Integrated Gradient(IG)[42]，Shapley Values(SHAP)[43]等.

以SHAP方法为例，SHAP方法认为一个特征对于输出变量的效应强度应该为：使用该特征的预测结果与不使用该特征的预测结果之差.将整个特征集合记作 F ={1,2,···,n}，预测输出结果需要选择一个特征子集，计算特征i的效应需要对比不含i的所有子集与对应添加i的子集的差别，即fS∪{i}(XS∪{i})−fS(XS).在所有满足条件的子集上取加权平均的结果即为特征i的Shapley值.SHAP方法将Shapley值作为特征的归因值，其他归因方法也会得到这样的归因向量.

基于归因分析的解释方法虽然描述的是因果关系，但一般不依赖因果术语，一些文献采用了因果的表述，本质上仍属于归因解释的框架.例如文献[44]提出一种针对端到端文本生成模型的因果解释框架，预测源文本中的单词对目标文本中单词的影响强度，相当于将源文本单词视为特征集合，针对每个目标单词的预测都给出1个对应的归因向量.文献[45]提出一种在不确定因素下图像分类模型的因果解释方法，其主要贡献在于对每个特征除了计算其归因值以外还会计算其置信度.文献[46]提出将机器学习模型整体视为一个SCM模型，然后计算每个特征对输出结果的平均处理效应，相当于将解释问题重新使用因果语言进行形式化，但在做法上与其他归因解释方法并无本质不同.

基于归因分析的解释方法一般将每个特征视为独立的变量进行考虑，而当特征之间存在相互影响时就必须借助因果理论进行刻画和求解.文献[47]基于SHAP方法将先验因果知识引入，提出非对称SHAP方法，其核心思想在于：原始Shapley值计算方法会将所有特征序列的置换平等看待，而非对称SHAP会调整这些置换的权重，例如将不符合因果顺序的置换的权重置为 0，从而将子节点的因果效应汇总归于祖先节点的因果效应.文献[48]同样基于SHAP方法，从另一个角度提出了引入因果知识的方式.SHAP 方法需要计算特征子集S下模型的期望输出v(S)，为保持样本位于数据流形之上，一般选择计算以XS=xS为条件下的期望.该文献认为，在给定因果图结构的情况下应使用do操作而非取条件的操作，即do(XS=xS)，由该方法得到的归因值称为因果Shapley值.同时，该文献利用中介分析将总体效应v(S∪{i})−v(S)拆解为直接效应与间接效应，展示了在不同因果结构下对于相同观测数据的解释存在的差异.

2.1.2 基于反事实的解释方法

基于反事实的解释方法是近年来新兴的一类模型解释方法，其中“反事实”作为一种因果术语指的是如果样本的部分特征发生了改变而其他特征不变将会怎样.一般而言，反事实解释方法会寻找一种样本特征处理方法使样本的预测结果发生显著改变，例如对图像的局部进行替换或遮挡从而改变分类类别等.与归因分析不同，反事实解释并不会提供每个特征的重要度，而是直接给出改变预测结果的途径，相当于给出信息“模型对样本X的输出为A而 不是B，是因为X具有特征f，如果该特征变为g则其输出会变为B”（本节所用符号与前文无关）.

Table 1 Application of Causal Methods on Interpretability Problems表1 因果方法在可解释性问题上的应用

文献[49-50]提供了一类典型的反事实解释方法.针对图像分类任务，需要从给定原始图像中选择一块区域使其替换为其他内容后变为目标类别.所替换内容为目标类别的1幅干扰图像的某一块区域.修改后的复合图像构成了原样本的一个反事实解释，如图5所示：

Fig.5 Example of counterfactual explanation [49]图5 反事实解释示例[49]

文献[51]在为图像分类模型构造反事实解释时避开了图像的修改合成过程，直接生成可读的文本解释，例如“它不是猩红丽唐纳雀，因为它没有黑色的翅膀”.文献[52]通过优化的方式求解图像的掩码，使得遮挡该区域后模型不再将其分类为原始类别.文献[53]在视频分类上应用反事实解释，选取视频中关键片段的关键矩形区域，并通过预测该区域的语言学属性为其搭配简单的文本解释，如“是骑行而不是滑板运动，因为姿势是坐着”.文献[54]利用局部语义纹理特征作为解释工具，称为断层线（fault-line），解释原始图像需要增减哪些语义特征才能改变为目标类别.文献[55]在强化学习中将行动影响建模为SCM，为智能体的行为做模板式的反事实解释，例如“智能体选择建造供应站而不是兵营，因为可以拥有更多供应站，有利于破坏对手更多的单位和建筑”.文献[56]提出反事实解释需满足可行性和多样性，并采用优化的方式求解反事实解释的集合.文献[57]为贝叶斯网络分类器构造反事实解释，求解值改变即引起结果改变的变量集合.文献[58]在反事实解释的基础上提出半事实（semi-factual）解释的概念，与反事实解释的区别在于其对于样本的修改接近改变输出但实际并未真正改变.文献[59]为针对图（graph）数据的分类器设计反事实解释方法，提出一种基于搜索的方法寻找反事实图.文献[60]针对以往基于算法的反事实样本构造方法过于耗时的问题，提出一种基于模型的反事实样本生成方法.文献[61]为集成树（tree ensemble）模型设计了反事实解释方法，建模为混合整数规划问题并进行求解.

文献[62]针对图像生成模型研究了一种特殊的反事实解释方法.由于图像生成模型的输入为无直观意义的噪声，一般的反事实研究不易产生有价值的解释，因此该方法不再针对输入特征进行反事实，而是将神经网络模型视为白盒SCM，在其内部表达节点上进行反事实，其目的是寻找模型中的独立生成机制，从而有助于对模型的理解.具体方法是寻找一些网络内部节点集合，使得在2幅图像上做数值交换后输出差异尽可能大，这些节点即反映了图像的关键生成机制.图6展示了该文献方法可通过2幅图像在关键内部节点上的数值交换实现反事实的图片混合效果.

Fig.6 Example of counterfactual image hybridization [62]图6 反事实图像混合示例[62]

基于反事实的模型解释方法相对于归因解释的优势在于其直接提供了改变当前模型预测结果的操作手段.然而一些文献指出，反事实解释提出的建议并不会考虑实际实施的代价，甚至可能是无法操作的.文献[63]研究了反事实解释偏离数据分布的问题，提出基于马氏距离和局部异常因子的代价函数约束反事实解释的可行度，将寻找可行反事实解释的问题转化为混合整数线性优化的求解问题.文献[64]在此基础上基于因果图分析了在多个特征上反事实操作的顺序问题，因果图可由因果发现技术获得.文献[65]研究了在特征为二值情景下的反事实解释的可行性问题，证明寻找最优反事实策略是NP难的，因此提出一种高效的随机算法进行近似求解.文献[66]研究了特征之间存在因果关联时如何提供可行反事实解释的问题，在假设因果图结构已知的情况下，用高斯过程建模结构方程的不确定性，提出个体和亚群体级别的2类可行性反事实解释，使用梯度优化的方式求解.

2.2 可迁移性问题

机器学习研究通常会在一个给定的训练数据集上训练模型，然后在同数据分布的验证集或测试集上进行测试，这种情况下模型的表现称为分布内泛化（in-distribution generalization）.在一般的应用场景中，机器学习模型会部署在特定数据环境中，并使用该环境中产生的数据进行模型训练，其性能表现可以用分布内泛化能力来度量.然而在一些场景中，目标环境中的标注数据难以获取，因此更多的训练数据只能由相似的替代环境提供.例如训练自动驾驶的智能体时由于风险过高不能直接在真实道路上行驶收集数据，而只能以模拟系统中所获取的数据为主进行训练.这种场景下的机器学习任务又称为域适应（domain adaptation），属于迁移学习（transfer learning）的范畴，即将源域（source domain）中所学到知识迁移至目标域（target domain）.这里的域（domain）和环境（environment）的含义相同，可以由产生数据的不同概率分布来描述，下文将沿用文献中各自的习惯称呼，不再对这2个概念进行区分.

在可迁移性问题中，因果理论的主要价值在于提供了清晰的描述语言和分析工具，使研究者能够更准确地判断可迁移和不可迁移的成分，有助于设计针对不同场景的解决方案.因果推断中关注的效应估计问题本质上是在研究改变特定环境作用机制而保持其他机制不变的影响，这与迁移学习中域的改变的假设相符，即目标域和源域相比继承了部分不变的机制可以直接迁移，而剩余部分改变的机制则需要进行适应.因此在因果理论的指导下，迁移学习中的关键问题就是建模并识别变与不变的机制.目前因果迁移学习一般假设输入X与输出Y之间有直接因果关系，重点关注无混杂因素情况下变量的因果方向和不变机制，如表2所示，以下介绍相关工作.

Table 2 Application of Causal Methods on Transferability Problems表2 因果方法在可迁移性问题上的应用

文献[77]是早期研究因果理论对机器学习指导作用的经典工作，主要使用结构方程模型研究输入变量X与输出变量Y之间的因果方向对可迁移性的影响：1）如果有X→Y，那么输入分布P(X)与条件分布P(Y|X)可视为独立的机制，目标域数据所提供的输入P′(X)信息对P′(Y|X)的预测不会产生直接作用，而输出P′(Y)却因包含了P′(Y|X)的信息而有助于预测；2）如果有Y→X，则输入分布P(Y)与条件分布P(X|Y)可视为独立的机制，结论将与1）情况完全相反，这种情况称为反因果（anti-causal）.正向因果情景1）中仅P(X)发生改变而P(Y|X)不变的情况常被称为协变量偏移（covariate shift, CovS）.文献 [70]针对实际情形中更常见的反因果迁移问题进行了进一步的建模，如图7所示：如果只有P(Y)发生了改变则称为目标偏移（target shift, TarS）；如果只有P(X|Y)发生了改变则称为条件偏移（conditional shift, ConS）；如果两者都发生了改变则称为广义目标偏移（generalized target shift, GeTarS）.这些工作为因果理论指导迁移学习奠定了基础.

后续许多工作沿用正反向因果框架展开，在不同的先验因果图结构下求解迁移学习问题.文献[78]探讨了在有多个源域提供数据的情况下如何求解各类反因果迁移问题.文献[67]提出协变量偏移情况下对P(Y|X)不变的假设过强，认为只需假设存在特征集合S使得P(Y|S)跨环境不变即可，并设计搜索算法寻找S.文献[68]针对目标偏移问题已有方法无法处理高维数据、连续数据和大规模数据等问题，提出一种新的标签变换方法求解，将源域的标签Y变换之后再重新训练或微调获得P(Y|X)模型.文献[69]研究条件偏移情况，基于变分自编码器结构学习X的隐变量表达，并引入对抗训练使语义表达与域表达解耦合，语义表达即可用于迁移.文献[71]指出在广义目标偏移的情况下使用文献[70]中的局部尺度变换方法可能无法满足需求，进而设计算法通过寻找条件可迁移成分（conditional transferable components）进行求解.

一些迁移学习的工作也考虑从其他角度引入因果理论和技术.文献[72]在因果图建模的基础上额外建模了结构方程，基于非线性独立成分分析构造目标域的伪样本对训练数据进行扩充.文献[73]利用因果图在一个虚拟的“密室逃生”任务上建模不同层次的因果结构，以将所学知识迁移到未见过的相似场景.文献[74]研究了一种特殊的模仿学习迁移任务，即演示者与学习者接收不同的传感器输入，如自动驾驶智能体上路时无法观测到学习时的指示灯信号，使用SCM分析可变与不变的部分以指导学习.文献[75]针对小样本学习（few-shot learning）这一特殊的域适应任务，认为预训练知识是特征和标签的混杂因素，采用后门调整消除其影响.文献[76]将域适应问题转化为增广的因果图上的推断问题，在多个源域的数据上进行结构发现，然后使用条件生成对抗网络建模.

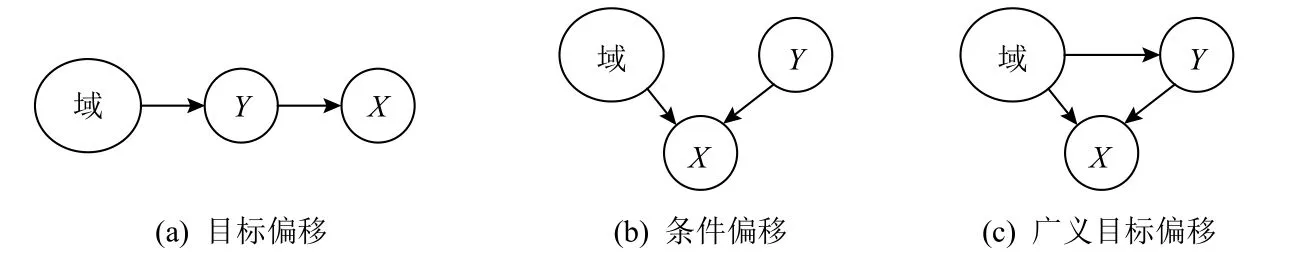
Fig.7 Causal graphs of three types of anti-causal transfer problems [70]图7 3类反因果迁移问题的因果图[70]

迁移学习问题与因果密切相关，对于跨环境不变机制的挖掘和利用始终是其核心问题之一.由于问题场景的不同会导致因果机制可变也可不变，无法统一下定论，需要具体问题具体分析，因果机器学习在这一问题上仍有宽阔的发展空间.

2.3 鲁棒性问题

迁移学习允许模型获得目标环境的少量数据以进行适应学习，然而在一些高风险场景中，可能需要机器学习模型在完全陌生的环境中也能正常工作，如医疗、法律、金融及交通等.以自动驾驶为例，即使有大量的真实道路行驶数据，自动驾驶智能体仍会面临各种突发情况，这些情况可能无法被预见但仍需要被正确处理.这类任务无法提供目标环境下的训练数据，此时模型的表现称为分布外泛化（out-ofdistribution generalization）.如果模型具有良好的分布外泛化能力，则称其具有鲁棒性（robustness）.

这类问题在未引入因果术语的情况下就已经展开了广泛的研究.如分布鲁棒性研究[79-81]考虑当数据分布改变在一定幅度之内时如何学习得到鲁棒的模型，常见思路是对训练样本做加权处理；对抗鲁棒性研究[8,82-83]考虑当样本受到小幅度扰动时模型不应当改变输出结果，常见思路是将对抗攻击样本加入训练.这类研究常常忽略变量间的因果结构，面临的主要问题是很难决定数据分布或者样本的扰动幅度大小和度量准则，这就使得研究中所做的假设很难符合真实场景，极大地限制了在实际中的应用.因果理论的引入为建模变量间的结构提供了可能，同时其蕴含的“机制不变性”原理为鲁棒性问题提供了更合理的假设，因为真实数据往往是从遵循物理规律不变的现实世界中采集获得.例如针对输入为X、输出为Y的预测问题，不考虑结构的分布鲁棒性方法会假设未知环境P′(X,Y)应当与真实环境P(X,Y)的差异较小，如限制联合分布的KL散度小于一定阈值；而考虑结构的因果方法则通常会假设机制不变，例如当Y是X的因时假设P′(X|Y)=P(X|Y)，在因果关系成立的情况下后者通常是更合理的.

一些从伪相关特征入手研究鲁棒性问题的工作虽然未使用因果术语，实际上已经引入了因果结构的假设.这些工作针对的往往是已知的伪相关特征，如图像分类任务中的背景、文本同义句判断SNLI数据集中的单条文本[84]、重复问题检测QuaraQP数据集中的样本频率[85]等.在实际场景中针对这些伪相关特征进行偏差去除（debias），以避免其分布发生变化时影响模型表现.这类工作隐含的假设是伪相关特征与目标预测变量没有因果关系.一种直接的解决方法是调整训练数据的权重，使得伪相关特征不再与预测变量相关[85].还有一类方法会单独训练一个仅使用伪相关特征预测的模型，然后将其与主模型融合在一起再次训练，完成后仅保留主模型[86-87].然而由于实际应用中通常很难预先确定伪相关特征，这类工作在解决鲁棒性问题上具有明显的局限性.

因果理论的引入对于解决鲁棒性问题提供了新的思路，主要的优势在于对变量结构的建模和更合理的假设.这类方法包括反事实数据增强（counterfactual data augmentation）、因果效应校准和不变性学习.如表3所示 ，反事实数据增强考虑从数据入手消除伪相关关系，因果效应校准通过调整偏差特征的作用来减轻偏差，不变性学习通过改变建模方式学习不变的因果机制，以下分别展开介绍.

2.3.1 反事实数据增强

反事实数据增强的核心思想是针对真实的因果关系额外构造反事实数据加入训练，以消除非因果变量与预测变量间的相关性，这里的因果关系通常是由人的先验认知给出的.“反事实”指的是对样本做改动，通过改变关键的因果特征使得预测结果改变.文献[114]给出了这类方法的有效性分析，下面对这类方法的相关工作进行简要介绍.

在自然语言处理领域主要关注文本分类任务中的数据增强.文献[88]针对文本数据中的性别-职业偏差，将性别相关词语替换成相反性别的对应词语作为数据增强.文献[89]同样针对性别偏差，认为直接替换性别词加入数据会造成统计属性的异常，因此建议改为随机替换原有数据，并额外提出一种姓名干预的方法将与性别相关的姓名词一同替换.文献[90]指出性别词替换的方法并不适用于某些性别与语法关联紧密的语言，如西班牙语和希伯来语，因此提出一套新的方法针对这类场景，在对性别词进行干预后重新推断新的词形和句法标签，在整条文本上进行调整.文献[91]针对文本情感分类任务中未知的伪相关特征问题，通过人工编辑文本使得改动幅度不大且情感类别反转，修改得到的文本作为训练数据扩充.文献[94]同样针对文本情感分类任务，通过匹配含义相近但标签相反的文本来寻找关键因果词，然后在原始文本上将因果词替换为其反义词，同时反转标签构成反事实数据.

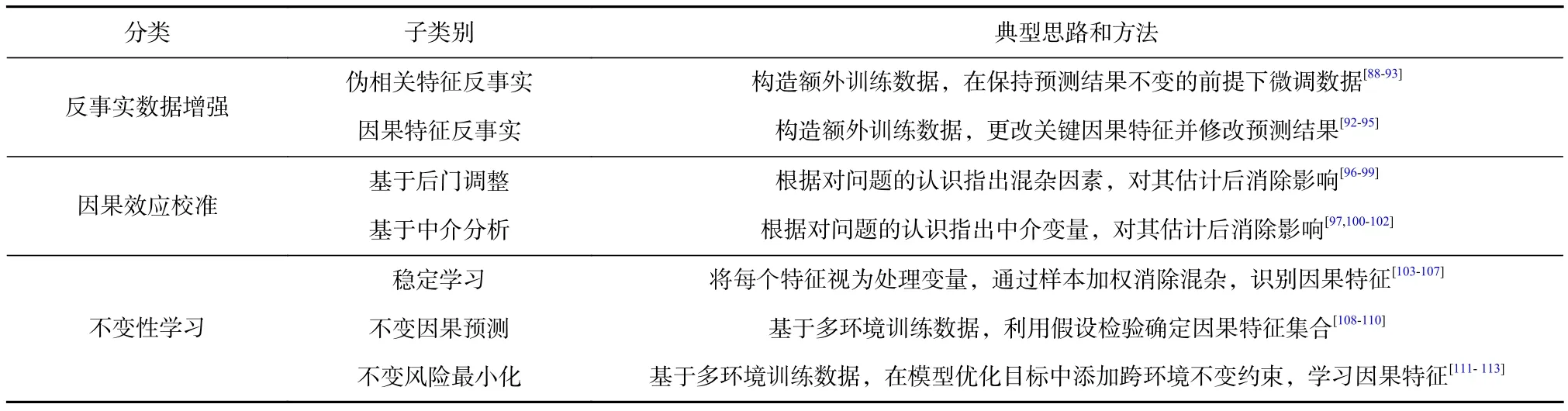
Table 3 Application of Causal Methods on Robustness Problems表3 因果方法在鲁棒性问题上的应用

在计算机视觉领域主要关注视觉问答(visual question answering, VQA)和图像分类等任务中的数据增强.文献[92]在VQA任务中使用生成对抗网络合成图像进行数据增强，针对语义实体进行相关或无关物体的移除，从而去除模型中的一部分伪相关关系.文献[95]提出2种针对VQA任务的数据增强方法，即遮挡图像中的关键区域，或者遮挡问题文本中的关键词，2种方法都不依赖人工标注.文献[115]使用SCM 对VQA 任务进行建模，通过推断外生变量的分布来构建改变图片或者改变问题的反事实数据.文献[116]提出在使用反事实数据时并不直接加入训练，而是与原数据配对构造对比损失，可以取得更好的效果.文献[117]提出在使用反事实数据增强方法时同时采用梯度监督正则项，可以进一步提高分布外泛化性能.文献[118-119]针对视觉−语言导航（vision-and-language navigation）任务，分别使用对抗训练寻找最难路径以及修改图像特征改变智能体行为的方式构造反事实样本.文献[120]借助因果独立机制概念，人为将图像生成过程分离为背景、形状和纹理的单独作用机制，从而构造出反事实图片的生成模型，将生成的伪造图片加入训练可提升图像分类模型鲁棒性.文献[93]在图像物体分类任务中利用人工标注的边界框信息，通过修改边界框内外的图像，分别构造类别改变和不变的2类反事实样本.文献[121]利用图像生成模型习得的隐状态特征表达，使用主成分分析方法识别关键因果成分，通过干预隐状态和风格迁移的方式分别构建反事实图像，提升了图像分类模型的鲁棒性.

反事实数据增强作为一种与模型无关的技术，除了直接应用于去除伪相关特征外，本身也是一种解决训练数据不足的有效手段.这种情况下也可以看作是过少的训练数据更容易带来各种伪相关特征问题.文献[122]针对命名实体识别任务中数据标注代价高的问题，使用替换实体的方法进行数据增强，并从SCM的角度阐述了方法的合理性.文献[123]研究基于语言的图片编辑任务中的数据稀缺问题，将语言指令关键词随机替换为同类别词进行数据增强.文献[124]关注强化学习任务中的一类局部机制可以解耦合的场景，如打台球任务中短时间内台球只会两两碰撞，提出一种局部因果模型，通过替换可解耦的局部状态实现数据增强.

2.3.2 因果效应校准

针对机器学习的鲁棒性问题，有一类工作会根据人的先验知识，对容易带来偏差的特征的作用进行调整，使其符合真实的因果效应，从而实现跨环境预测的稳定性.本文将这类研究统称为因果效应校准.典型的思路是根据问题的特点提出对应的因果图假设，然后针对混杂因素变量使用后门调整进行校准，或者针对中介变量使用中介分析进行校准等.以下对各个工作分别进行简要介绍.

文献[96]研究法庭意见文本生成任务，由于原告通常会在很可能被支持的情况下提起诉讼，因此主张是否受法庭支持成为了原告声明和法庭意见之间的混杂因素，使用后门调整处理后减少了支持主张的意见文本，更符合真实判决结果.文献[97]在视觉对话任务中根据因果图结构提出2种校准策略（如图8所示）：1）切断对话历史H对于未来对话文本A的直接效应而仅保留经由问题文本Q的中介效应；2）建模未观测混杂因素并使用后门调整消除其带来的伪相关作用.文献[98]在视觉常识推理等任务中，认为图像中的物体标签是混杂因素，使用后门调整处理后获得更准确的图像特征表达.文献[99]在弱监督语义分割任务中，只利用图像标签作为监督信号，并认为图像标签是混淆因素，通过后门调整改善分割质量.文献 [100]研究场景图（scene graph）生成任务，由于训练数据中缺少针对图像中物体位置关系的精确描述，如本因该描述成“站在······上面”和“躺在······上面”，却使用了“在······上面”这种缺乏信息的描述，提出物体标签是图片特征对位置描述关系的中介变量，这一中介效应应当被削弱，因此在预测描述关系时使用TDE来代替TE.文献[101]指出分类问题中长尾分布的尾部预测不准的部分原因是在优化算法中使用了动量，而动量是输入变量和输出变量间的混杂因素，且动量在头部的投影是输入到输出间的中介变量，因此同时采用后门调整和TDE方法进行校准.文献[102]研究视觉问答任务中问题文本引起的语言偏差问题，使用全间接作用TIE代替原有预测，避免问题文本对回答产生直接作用，获得更高的预测准确率.

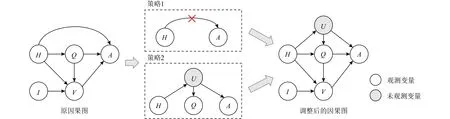
Fig.8 Causal graph and two calibration strategies in visual dialogue tasks [97]图8 视觉对话任务的因果图和2种校准策略[97]

除了后门调整和中介分析以外，也有工作采用其他方法实现因果效应校准.文献[125]在模仿学习任务中，由于专家对环境的观测与智能体的观测并不一致，因此定义了一种部分可观测的SCM进行建模和求解.文献[126]研究了一类运行时混杂（runtime confounding）的问题，即模型在训练时可以访问所有特征，而在测试时却有部分特征无法获取，采用双稳健估计DRE算法解决该问题.文献[127]针对图像分类中的组合泛化问题，认为标签和属性相互独立且图像由两者生成，采用反向因果建模求解.文献[128]研究词向量中性别偏差的问题，认为单纯使性别无关词向量垂直于性别定义词向量不足以解决问题，因为性别无关词仍可能被聚类为同一簇从而提供偏差信息，因此使用半兄弟回归（half-sibling regression,HSR）[129]消除两者之间的混杂因素.文献[130]同样针对词向量的性别偏差问题，提出一种反事实生成的方法，将词向量解耦成性别相关和性别无关的2部分，通过反转性别标签得到性别相反的词向量，与原词向量取平均后得到中性的词向量.文献[131]使用HSR 技术为词向量降噪，使内容词和功能词有更准确的含义表达.文献[132]在视觉问答任务中使用前门准则修正图像和问题对回答的因果作用，使模型中的注意力机制更好地捕获真实因果关系.

2.3.3 不变性学习

机器学习中的鲁棒性问题与现实物理世界中的因果不变性机制有着紧密的联系.由于实际应用考虑的往往是宏观的物理过程，任何因果机制都难以保证一成不变，因此考虑无任何约束的鲁棒性问题意义不大且没有必要，重要的是满足常见环境下的需求.要达到这一目标，建模常见环境中不变的因果机制就成了实现模型鲁棒性的必然需求.本文将这类研究统称为不变性学习.不同于反事实数据增强和因果效应校准等方法需要对伪相关特征有一定的认识，不变性学习可以对伪相关特征未知的情景进行处理.常见思路包括稳定学习（stable learning）、不变因果预测（invariant casual prediction, ICP）和不变风险最小化（invariant risk minimization, IRM），以下分别展开介绍.

稳定学习[103]指的是要求模型在不同的环境中具有稳定的性能表现，既要有较高的平均表现，也要有较低的方差.稳定学习假设预测目标仅由一组因果特征决定，其预测作用具有不变性，而其他特征为伪相关特征.稳定学习一般利用单个环境的数据，通过样本加权的方式消除伪相关特征的影响，从而使因果特征被保留下来.文献[104]提出因果正则化逻辑回归（causally regularized logistic regression, CRLR），对每个样本学习一个权重，在优化经验风险的同时需使得以每个特征为处理变量（treatment variable）的协变量分布尽可能一致，所学得的关键特征更符合人的判断标准.文献[103]明确提出稳定学习的概念，并提出深度全局平衡回归（deep global balancing regression,DGBR）算法，使用自编码器（auto-encoder）将特征降至低维空间，然后采用与CRLR相同的思路求解，根据学到的权重检查每个协变量条件下处理变量是否与预测结果变量独立，不独立的即为稳定特征.文献[105]指出DGBR算法可能存在模型设定偏误（misspecification）问题，提出去相关加权回归（decorrelated weighting regression）算法，引入特征非线性变换解决这一问题.文献[106]同样针对设定偏误问题，指出输入特征之间存在的共线性特点会放大模型设定偏误带来的误差，因此提出一种样本重加权去相关算子（sample reweighted decorrelation operator）消除共线性.文献[107]针对CRLR和DGBR只能针对线性框架的缺陷，提出基于随机傅立叶特征的非线性特征去相关算法StableNet，可以更有效地应用于图像等复杂数据类型.目前基于样本加权的稳定学习方法对于数据有一个较强的假设，即对于可能存在的因果特征和伪相关特征的组合均需要存在对应的训练样本，这在实际场景中可能难以满足.因此在该假设不成立时如何应对仍是有待研究的课题.

不变因果预测ICP[108]方法的思路是借助多个环境的数据来确定跨环境不变的特征.文献[108]在线性框架下提出了ICP，基于假设检验的方式确定不变因果特征集合，同时还可以给出置信区间.文献[109]将这一方法拓展至非线性框架，并且可以适用于连续环境.文献[110]将ICP方法进一步拓展至时间序列数据上.基于ICP的方法均要求因果变量是输入特征的子集，因此一般不适用于高维复杂数据如图像和文本等，然而其思想对这类问题的解决提供了很好的启发作用.

不变风险最小化IRM[111]方法延续了ICP的思想，同样是借助多个环境的数据来学习跨环境鲁棒的模型，但不再从输入特征集合中选择因果特征，而是使用模型抽取特征.IRM认为机器学习模型可以拆分为特征抽取器和预测器2个部分，即输入样本首先通过特征抽取器得到分布式表达，然后预测器将该表达映射为目标输出结果.IRM假设因果特征应当使得预测器保持跨环境不变性，这种不变性约束被转化为损失函数中的正则项，即在各个环境数据上损失函数对于预测器参数的梯度尽可能为零.许多后续研究沿用或者借鉴了IRM的方法.文献[112]考虑强化学习在多环境中的泛化问题，假设下一状态仅与当前状态构成因果关联并构建因果图，使用IRM学习状态摘要表达，然后对接下游任务.文献[133]考虑模型隐私保护问题，证明了因果学习得到的模型相对于相关学习得到的模型的分布外泛化误差更小，且能够抵抗隐私攻击，方法使用IRM实现.文献[113]针对IRM所需要的多环境数据的构造问题，提出在没有显式环境类别标注时可以引入辅助的环境推断任务，直接由单一数据集构建多环境子集.

除以上常见方法外，也有研究工作基于不变性学习探索了其他方案.文献[134]针对反因果任务使用因果图建模（如图9(a)所示），提出Deep CAMA方法解决模型鲁棒性问题.除输入变量X和输出变量Y以外还引入了其他未观测变量，分为可干预的变量M及不可干预的变量Z.对分解的因果图各部分使用神经网络建模，利用原始训练数据和干预过的数据进行证 据 下 限 优 化（evidence lower bound optimization）.其中干预数据指的是对变量M的do操作，具体的干预数值可以通过推断获得，而原始训练数据被视为do(M=0)操作下的观测.文献[135]同样针对鲁棒性问题使用因果图建模（如图9(b)所示），提出潜在因果不变模型（latent causal invariance model, LaCIM），认为不同的域Y决定了混杂因素C，进而生成构成输入h的2组特征Z和S，其中S决定了 输出结果Y，而Z与Y无因果关系.除D可变以外，其他因果机制视为不变.该方法利用变分自编码器（variational auto-encoder）将变量X和Y编码至隐空间，并视为由代表S和Z的2部分组成，两者共同通过解码器重构X，同时令S通过单独的解码器重构输出变量Y.在测试阶段，给定输入X后输出Y可以由因果图上的推断过程获得.文献[136]认为图像数据由内容C和风格S共同决定，对于分类任务而言不论风格怎样改变，内容对类别的作用机制是固定不变的，即P(Y|C,do(S=s))=P(Y|C,do(S=s′)).因此利用大量无监督图像数据，通过旋转、裁剪、灰度调整等风格干预操作构造成对图像，使特征抽取模型所习得的特征表达在成对的图像对实例判别（instance discrimination）任务有相似的预测作用.在无监督预训练之后得到的特征抽取模型可用于下游任务的学习，能够有效提升分布外泛化能力.文献[137]认为在分类任务中相同物体的不同表现应当具有不变的特征表达，在模型优化目标中添加额外的正则项，要求同类别的随机选取的2个样本具有较高的匹配程度，其中匹配程度的度量方式通过对比学习（contrastive learning）习得.文献 [138]在多实例学习任务中，认为实例集合的标签取决于集合中的某些关键实例，将其称为因果实例（causal instance），且认为利用因果实例判别标签的过程在协变量偏移场景下具有不变性.因此采用RCM建模并利用回归估计识别因果实例，然后通过与因果实例进行比对来确定集合判别结果.

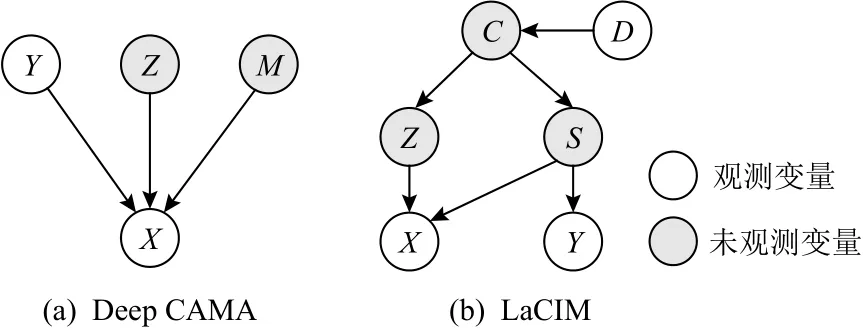
Fig.9 Causal graph of invariance-learning methods [134-135]图9 不变性学习方法的因果图[134-135]

基于不变性学习解决模型鲁棒性问题是一种在机器学习中引入因果的自然方式，同时也有较好的发展前景.目前已有工作只是在该领域的初步尝试，需要针对不同任务和数据设定不同的假设，并分别设计求解方案，缺乏统一的方法论的指导，仍有待进一步研究探索.

2.4 公平性问题

机器学习中的公平性（fairness）指的是，对于特定的敏感特征如性别、年龄、种族等，不同的取值不应该影响某些任务中机器学习模型的预测结果，如贷款发放、法律判决、招生招聘等.公平性对于机器学习在社会决策中的应用是十分重要的考虑因素，与因果有密切的关系，直观上体现为敏感特征不应成为预测结果的因变量.模型中存在的不公平常常由伪相关特征问题导致，因此公平性也可以视为针对敏感特征的鲁棒性，但有着自己独有的术语和研究体系.下面首先介绍一下公平性的基本概念，然后介绍因果理论在公平性问题中的应用.

公平性的定义和度量指标目前十分多样化，并没有完全统一确定，不同的定义所反映的问题也有所不同，甚至可能是相互不兼容的[139].为便于表述，记敏感特征为A，其他观测特征为X，真实输出结果为Y，模型为f，模型预测结果为=f(A,X)（本节所用符号与前文无关）.早期公平性问题的相关工作并没有考虑因果，最简单直白的方式是在决策时避免使用敏感特征[140]，即f(A,X)=f(X).然而这一方案显然是不够的，因为其他特征中也可能会包含敏感特征的信息.因此一般会考虑个体级别的公平性或者群体级别的公平性的度量，并设计方法实现.个体公平性（individual fairness）通常会限制相似的个体之间应该有相似的预测结果[141]，难点在于相似性指标的设计.群体公平性（group fairness）会定义不同的群体并设置度量指标使得各个群体之间差异尽可能小，一种思路是人群平等（demographic parity）[142]，希望在不同敏感特征取值的群体中预测结果的分布一致，即另一种思路是机会均等（equality of opportunity）[143]，希望在那些本该有机会的人群所获得的机会不受敏感特征的影响，即P还有一种思路是条件公平（conditional fairness）[144],希望在任意公平变量F条件下不同敏感特征群体的结果一致，即这些定义并不考虑特征内部的依赖关系，对模型的决策机制也没有区分性，在更细致的公平性分析中难以满足要求.因果理论的引入为公平性研究起到了极大的推动作用，许多概念必须借助因果的语言才能表达，如表4所示:

Table 4 Application of Causal Methods on Fairness Problems表4 因果方法在公平性问题上的应用

较早引入因果的公平性研究工作是反事实公平性（counterfactual fairness）[145].这里的反事实指的是，仅仅改变个体的敏感特征而保持其他特征不变，包括未观测的特征.反事实公平性指的是对任何个体的反事实操作都不应当影响其预测结果，即这种定义避免了个体公平性相似性指标设计困难的问题，同时相对于群体公平性又有更高的要求.具体实现公平性的方法通常是利用数据推断未观测变量作为数据增强，或者避免使用敏感特征及其在因果图上的后继节点作为模型输入.反事实公平性的一个重要研究内容是特定路径（pathspecific）上的反事实公平性，即考虑在因果图上从敏感特征到预测结果的不同路径，造成直接影响的路径会引发公平性，而间接影响的路径则未必引发不公.文献[146]针对这一问题提出“未解决的歧视”（unresolved discrimination）概念，指出任何基于观测的标准均无法判断模型是否表现出未解决的歧视问题，通过施加干预不变性的约束可以解决这一问题.文献[147]同样针对特定路径的反事实公平性，将问题转化为约束优化问题，使用逆概率加权IPW方法求解.文献[148]针对前面2项工作容易丢失个性化信息的问题，提出一种基于隐变量的方法修正在不公平路径上敏感变量的后继节点的观测.文献[149]延续文献[148]的研究内容，将个体级别的讨论拓展到子群体的级别，并提出方法解决这一框架下的可识别性问题.文献[150]研究了反事实公平性中的可识别性问题，即反事实结果是否能够通过观测数据获得唯一解.该工作指出当且仅当敏感特征后继和预测结果的祖先存在交集时不可识别，这种情况下虽无法确定唯一解，但可以计算上下界.文献[151]研究了文本数据中国家、职业、姓名等敏感特征对情感预测的反事实公平性问题.文献[152]在文本分类任务中提出反事实符号公平性（counterfactual token fairness）新概念，即针对敏感词的反事实公平性，提出敏感词替换和反事实逻辑匹配的方法解决该问题.

除了反事实公平性，一些工作也从其他角度引入了因果技术.文献[153]研究了多模型级联构成的决策系统的公平性问题，如果单个模型存在不公平问题则会导致整体不公平，但逐个模型进行处理的效率太低，因此将整体系统建模为SCM，视单个模型的调整为因果图上的软干预，从而实现全局的高效求解.文献[154]考虑多步决策中存在数据缺失时的公平性问题，使用因果图建模这一问题，并提出一种去中心化的方法避免公平性算法依赖那些缺失后无法恢复的信息.文献[155]考虑从构建数据集的角度实现公平性，利用生成对抗网络建模在敏感特征受到干预时的生成机制，通过控制干预下的样本生成过程，消除数据中的不公平因素.文献[156]基于RCM提出2种新的群体公平性指标：平均因果效应公平（FACE）和处理组平均因果效应公平（FACT），相当于反事实公平性在群体上的平均度量，使用倾向性得分方法IPTW进行因果效应估计.文献[157]尝试基于中介分析将全局变化量（total variation, TV）拆解成多个细粒度的度量，包括反事实直接效应、反事实间接效应和伪效应.文献[158]延续文献[157]的工作，将方法拓展到TV以外的其他度量指标，并给出了这类问题的求解方法.文献[159]针对达到公平性需要重新训练模型的问题，提出一种基于样本加权的反事实分布修正方法，可以避免重新训练的开销.文献[160]考虑动态系统中的公平性度量问题，将动态系统建模为SCM，则公平性度量就成了因果效应估计问题，使用双稳健估计DRE方法进行处理.

目前针对机器学习公平性问题的研究已经与因果密切相关，包括描述语言、建模方法和求解手段都在一定程度上依赖因果研究的相关成果，预计未来因果理论在这一方向将持续起到不可替代的作用.

2.5 反事实评估问题

反事实评估（counterfactual evaluation）指的是机器学习模型的优化目标本身是反事实的，这通常出现在使用有偏差的标注数据训练得到无偏模型的情景，例如基于点击数据的检索和推荐系统学习任务.由于任务本身需要反事实术语进行表述，因果理论对这类问题的建模和研究起到了关键性的作用，如表5所示：

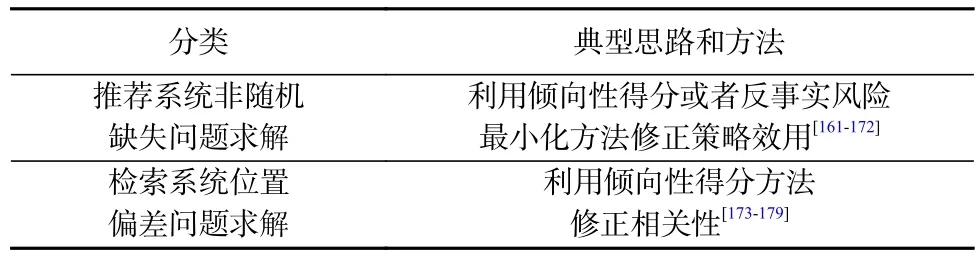
Table 5 Application of Causal Methods on Counterfactual Evaluation Problems表5 因果方法在反事实评估问题上的应用

以推荐系统为例，这类任务的目的是根据用户的意图和喜好向用户展示相关性更高的物品，如文档、商品及广告等.由于难以获得物品真实相关性的人工标注，实际应用中通常会使用用户的点击（click）数据指导模型学习.然而系统每次只能向用户展示部分物品，这就使得未展示物品无法被估计相关性，从而对系统策略的评估带来偏差.考虑假设所有物品都被展示的情况下的点击率即属于反事实评估问题.由于未展示物品是由系统策略决定而非完全随机，其点击数据的缺失也是非随机的，因此也被称为非随机缺失（missing-not-at-random, MNAR）问题.文献 [180]在广告推荐系统中使用因果图建模这类问题（如图10所示），并指出这种情况下的系统评估是反事实的.这种情况需要估计物品是否被观测这一变量对是否被点击这一变量的因果效应，可以用RCM建模，使用逆倾向性得分（inverse propensity scoring, IPS）方法修正偏差.这里的倾向性得分指的是物品被观测到的概率，用得分的倒数作为权重为训练样本加权，即可消除偏差.记用户特征为x，物品特征为y，向用户展示物品的策略为h，倾向性得分为p，是否被点击为δ（本节所用符号与前文无关），则对于展示策略效用的无偏IPS估计为

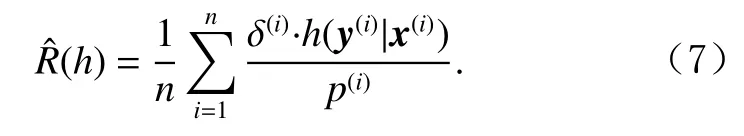
文献[161]称这类任务为从Bandit反馈日志中批量学习（batch learning from logged bandit feedback, BLBF），在IPS的基础上额外采用权重裁剪和方差正则，提出一种新方法称为反事实风险最小化（counterfactual risk minimization, CRM）:

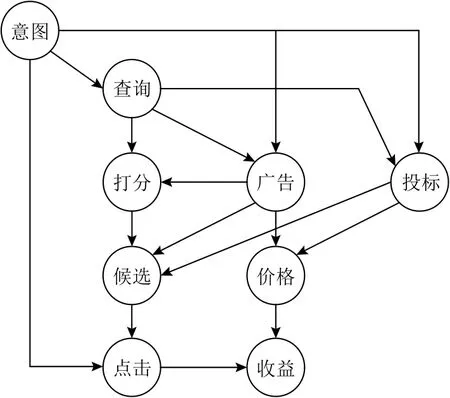
Fig.10 Causal graph in advertising recommendation systems[180]图10 广告推荐系统的因果图[180]

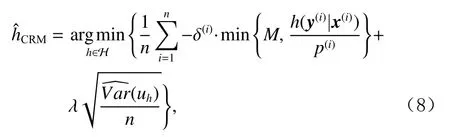
其中，M为权重裁剪参数，λ为方差正则权重，uh为带权重裁剪的IPS估计值.

大量工作延续IPS和CRM方法展开研究.文献[162]指出CRM中存在倾向性过拟合问题，提出自归一化估计方法解决.文献[163]指出CRM中的方差估计需要遍历整个训练集导致计算开销大，提出一种变分散度最小化方法解决.文献[164]从贝叶斯视角重新分析CRM，提出一种更易实现的新正则化方法.文献[165]针对系统行为空间极大的情况提出分布鲁棒的CRM 算法.文献[166]将IPS 推广至更广泛的评价指标，并针对推荐系统任务提出倾向性得分的估计方法.文献[167]将IPS拓展至隐反馈问题，即只有点击记录而没有未点击记录的情况.文献[168] 额外考虑推荐系统的使用会改变未来用户行为的问题，基于IPS提出一种因果嵌入表达方法.文献[169]提出在IPS中使用估计的倾向性得分要比真实的倾向性得分获得更低的方差.文献[170]考虑推荐的集合被捆绑为一个整体同时选择推荐或者不推荐，因此原有IPS作为针对单个物品的方法在此并不适用，提出一种变分样本加权的方法来解决.文献[171]指出由于展示物品只是整体的一部分，因此整体系统的展示机制不可识别，提出一种对抗学习的方案改进IPS.文献[172]考虑BLBF问题中反馈信息存在序结构的情况，由于CRM 方法无法利用结构信息，因此提出一种基于域适应的算法进行求解.BLBF这一建模框架也被用于推荐系统以外任务，如文献[181]在语义解析任务中引入人工反馈信号，同样使用IPS方法进行反事实评估.

检索系统中也会面临类似的MNAR问题，这类应用需要对展示物品进行排序，与用户需求相关性更高的物品应当排在更靠前的位置.这种情况下用户选择物品的点击行为会受物品列表的展示位置的影响，位置越靠后则越不容易被用户观测到，进而使点击率也偏低，因此这一问题也被称为位置偏差（position bias）问题.文献 [173]指出了位置偏差问题，并使用IPS方法进行处理，其中倾向性得分指的是物品在当前位置被观测到的概率.一个关键的问题是如何估计倾向性得分，一般需要在线上系统中单独收集数据进行估计.文献[174]指出直接采用随机策略估计倾向性得分会影响用户体验，提出一种期望最大化算法避免随机策略；文献[175]指出倾向性得分估计和消除位置偏差的任务互为对偶任务，提出对偶学习方法，同时学习2个模型.一些工作也考虑对IPS进行改进，文献[176]对IPS方法进行扩展，能够适配一般的加性排序指标和非线性模型；文献[177]针对IPS稳定性问题，提出使用采样代替加权的做法，使训练更稳定；文献[178]将IPS 由点击模型推广到级联模型.文献[179]对比了IPS和在线学习方法，指出IPS在偏差和噪声较小的情况下优于在线学习方法.

反事实评估问题在检索和推荐系统中的技术已经相对成熟和固化，许多文献除了沿用IPS和CRM的概念以外未必会使用额外的因果术语进行表述，但这并不影响因果理论在其中的根基作用.未来如果出现其他需要使用反事实评估的场景，也可以继续通过因果分析与已有技术快速建立联系.

2.6 其他问题

因果机器学习的研究工作种类十分丰富，除了在可解释性、可迁移性、鲁棒性、公平性和反事实评估这些主要问题上的研究以外，还有部分其他方面的研究.以下选择其中值得关注的部分工作进行简要介绍.

因果理论在一些需要建模变量间结构信息的情况下十分有效.文献[182−184]研究多臂老虎机问题（multi-armed bandit）中变量存在因果结构的情况，称为结构老虎机（structured bandit）问题，指出忽略因果结构可能导致次优的解，并设计各类方法求解.文献[185]指出模仿学习中忽略因果关系会导致错误识别问题，即更多的学习数据反而导致性能下降.因此将变量组织成图结构，随机连接一些节点，依据性能表现学习背后的真实因果图.文献[186]研究机器学习任务在特征和输出之间存在因果图的情况下，可以在预测的同时进行因果发现，作为一种正则化手段可以使回归任务更准确.文献[187]研究特征之间存在结构关系的解耦表达任务，在模型中设计SCM层结构，借助对特征的额外标注学习特征表达，得到的解耦模型可实现干预或反事实下的生成.

因果理论中的反事实思想和技术为多个领域的问题提供了求解思路.文献[188]在不完全信息博弈问题中，使用反事实的思想设计了反事实遗憾最小化（counterfactual regret minimization）算法，已成为求解该问题的重要方法[189-192]，其中反事实指的是将当前策略替换为最优策略会带来多大改进.文献[193]研究强化学习中多类别分布下的SCM 可识别性问题，通过选择风险最高的反事实轨迹，提供离线策略评估方案，为专家提供诊断建议.文献[194]研究离线强化学习问题，将原有的在自身策略下的探索改为基于日志的反事实探索，获得性能提升.文献[195]研究使用Actor-Critic方法训练场景图生成模型，提出在Critic 模型中使用反事实结果作为基线可以提升生成效果.文献[196]研究对话生成任务，借助已经生成的回复文本来构建反事实回复文本，获得更好的生成质量.文献[197]在文本分类任务的注意力监督方法中，使用反事实推理替代人工标注，得到了优于人工标注的结果.文献[198]在弱监督视觉语言举证（vision-language grounding）任务中提出一种反事实对比学习方法提升了举证效果.

因果机器学习本身也提出了更高层级的问题，即干预和反事实结果预测问题，这需要机器学习和因果推断2个领域的协作才能完成.文献[199]和文献[200]分别基于生成对抗网络和变分自编码器实现干预和反事实下的图像生成能力.文献[201]和文献[202]分别在文本生成领域提出和求解反事实故事重写问题.文献[203]在文本生成任务中根据不同的属性要求针对已有文本生成不同的反事实文本.文献[204]尝试解决多智能体任务中针对环境改变的反事实提问.文献[205]在3D物理引擎世界中预测改变初态后的反事实未来发展.

3 总结与展望

本文介绍了因果相关的概念、模型和方法，并着重对因果机器学习在各类问题上的前沿研究工作展开详细介绍，包括可解释性问题、可迁移性问题、鲁棒性问题、公平性问题和反事实评估问题等.从现有的应用方式来看，因果理论对于机器学习的帮助在不同的问题上具有不同的表现，包括建模数据内部结构、表达不变性假设、引入反事实概念和提供效应估计手段等，这在缺少因果术语和方法的时代是难以实现的.有了因果理论的帮助，机器学习甚至可以探讨过去无法讨论的问题，如干预和反事实操作下的预测问题.

对于可解释性、公平性和反事实评估问题，因果理论和方法已成为描述和求解问题所不可缺少的一部分，且应用方式也渐趋成熟.这是由于对特征的重要程度的估计、对模型公平性的度量和对反事实策略效用的评估均属于因果效应估计的范畴，问题本身需要使用因果的术语才能得到清晰且完整的表达，因果推断的相关方法自然也可以用于问题的求解.可以预见，未来这些问题将继续作为因果理论和方法的重要应用场景，伴随因果推断技术的发展，向着更加准确和高效的目标前进.

对于可迁移性和鲁棒性问题，目前所采用的因果相关方法大多还处于较浅的层次，有待深入挖掘探索.在这些问题上，因果推断的相关技术不易直接得到应用，这是由于这类问题的目标不再是单纯估计因果效应或者发现因果结构，而是需要识别跨环境不变的机制.这对于因果而言是一项全新的任务，需要研究新的方法来求解.在机器学习尤其是深度学习中，这项任务的主要难点在于数据的高维复杂性.对于图像和文本等数据而言，其显式特征高度耦合，难以从中提取出有效的因果变量，阻碍了效应估计和结构发现等后续分析手段.目前所采用的反因果迁移、反事实数据增强和因果效应校准等手段大多只能针对可观测的已知变量进行处理，适用范围受到很大限制.相对地，不变性学习有能力处理未知的伪相关特征并识别因果特征，具有良好的发展前景.然而目前的不变性学习方法也存在局限性，主要在于对数据做了较强的因果结构假设，一方面数据可能无法满足假设而又缺少验证假设的手段，另一方面需要为满足不同假设的数据设计不同的方法而缺乏通用性.因此，未来在这些方向上都值得开展研究.一种思路是继续针对具体任务做出不同的因果结构假设，并设计对应的学习算法，这就需要构建成体系的解决方案并配备验证假设的手段；另一种思路是从数据本身出发，推断和发现潜在的因果结构，这就需要研究全新的方法来突破由数据的高维复杂性带来的障碍.

从因果机器学习的研究进展来看，机器学习领域的因果革命将大有可为.不可否认，当前正处于因果革命的起步阶段，由于现实问题存在极高的复杂性，这一革命的历程也将曲折而艰辛，需要更多的研究和支持.希望更多的研究者能够加入到因果机器学习的研究中来，共同创造和见证因果革命的新时代.

作者贡献声明：李家宁和熊睿彬合作完成文献调研、内容整理和文章写作，对本文具有同等贡献；兰艳艳对本文选题、组织结构和文章写作提供了关键性的指导意见；庞亮对本文组织结构和部分内容提供了重要的指导意见；郭嘉丰和程学旗对本文的选题提供了重要的指导意见.