基于工厂物流中遗传算法的多AGV路径规划研究

付博言 张一帆

(广西科技大学经济与管理学院 广西柳州 545006)

进入21世纪以来，中国加入世贸组织，对外贸易出口日益增加，伴随而来的经济体量大幅度增加，一些小众企业不得不转型升级，为了让企业的效益得到最大化，很多企业先后引入自动化物流来提高企业自身的生产效率[1]，而AGV作为自动化中的一环在提高生产效率、企业效益方面尤为关键，有着更加广阔的市场应用前景，在未来的发展中它将可能完全替代人力成为主要的劳动输出。

AGV在我国的发展时间较为短暂，直到20世纪六七十年代，北京起重运输机研究所、中科院邮政研究规划院联合清华大学在内的国内多家理工类高等院校进行AGV小车的研发，1975年，北京起重运输机研究所成功制造出国内首台AGV小车[2]，并进行了产品的量产。

AGV的量产成功地迈开了第一步，如何提高AGV在实际生产中的运用显得尤为重要，在生产中AGV通过牵引、拉拽装载货物的货架将其送到指定地点就算完成一次运输任务，为了提高AGV的运输效率，Dijkstra首先提出了AGV最短路径问题的研究[3]，此后，AGV的路径算法被越来越多地研究出来，国内学者对于路径算法的理论研究提出了自己的见解，其中陈华志[4]通过神经网络并行性和融合性，研发了一种基于神经网络的AGV小车路径规划的算法，提高了路径规划的速度；肖本贤(2004)[5]运用模糊逻辑实现对超声波和视觉传感器的数据进行融合，使AGV小车能在不确定的环境中进行自主导航；李建华等(2005)[6]提出了一种AGV轨迹更理想自适应的轨迹跟踪控制方法。

国内众多学者提出的路径优化研究都是在模糊神经算法、免疫网络算法、Dijkstra算法等众多算法的基础上，通过对AGV小车在运输过程中的运行速度、运输环境中的自主导航能力进行优化改良[7]。

本文基于遗传算法对多AGV小车的路线问题进行优化，相较传统的AGV单一路线运输，拥有固定的路线以及需要运输的固定位置的货物，多AGV路线研究借助于计算机的智能算法对多辆AGV小车的路线进行模拟分析[8]，在运输速度与可控性尽可能最大化的情况下将位于不同区间货架上的不同货物位置坐标化，然后找到每一辆小车通过这些位置坐标的用时最短、效率最高的路径。

1 研究方法

1.1 遗传算法

基本遗传算法是一种模拟自然演变寻找最优解的方法。通过模拟自然选择的方式来复制初始群体中的个体，不断发生交叉、变异等操作产生优于上一代且更适应于新环境的群体，不断通过迭代进化直到产生最优个体。遗传算法具有不断优化的特性，采用遗传算法来对多AGV小车路径进行优化可得出最优的路线选择。

1.2 模型构建

1.2.1 模型环境构建

柳州某物流中心位于柳州市柳南区，是现代物流基地的重点物流中心，该物流中心是集工程机械、汽车配件、高新技术等产业为一体的大型综合工业园区，为了提高企业效益，公司采用AGV小车进行物料和货物的运输，由于物流中心的货物放置过于分散且该物流中心的AGV小车运行只能进行单一的固定线路运输，为了增加运输效率进而提升效益，决定对单一的固定运输线路进行优化并增设多条AGV运输线路。首先对AGV出库运输货物建立出库模型，AGV起始点为出库月台，其次采用数据为随机数据设计一百个出库货位点，并用0—100序号进行标号。最后用Excel软件进行随机选择坐标点，坐标点在(0，0)至(99，100)，建立(0，100)范围内的二维坐标系，出库月台点设计坐标为(100，50)，对应序号为0，如图1所示。

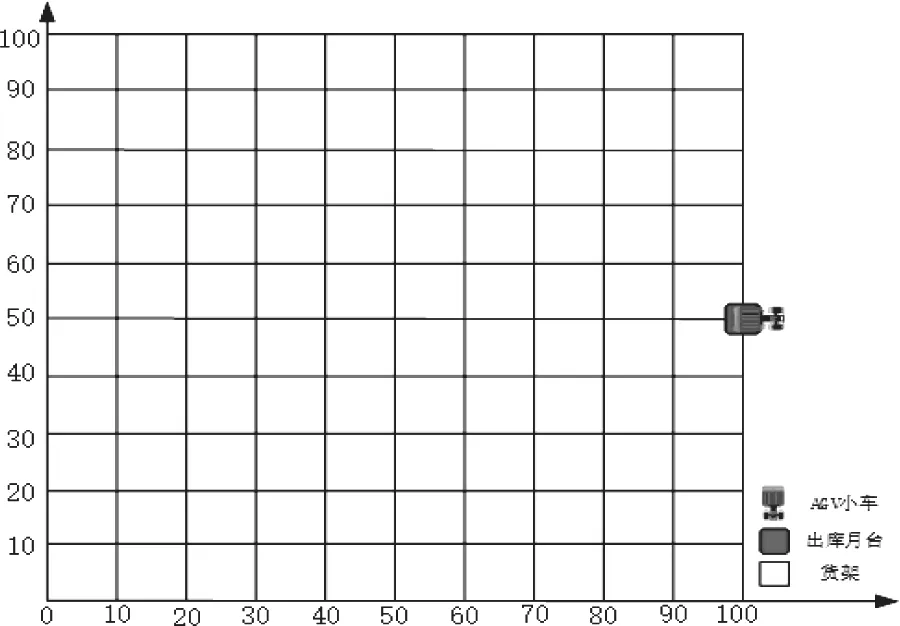
图1 柳南物流中心出库模型二维平面图

1.2.2 模型约束构建

根据出库需求时间区间进行约束条件设计。

最优值求解

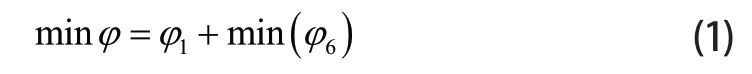
具体公式

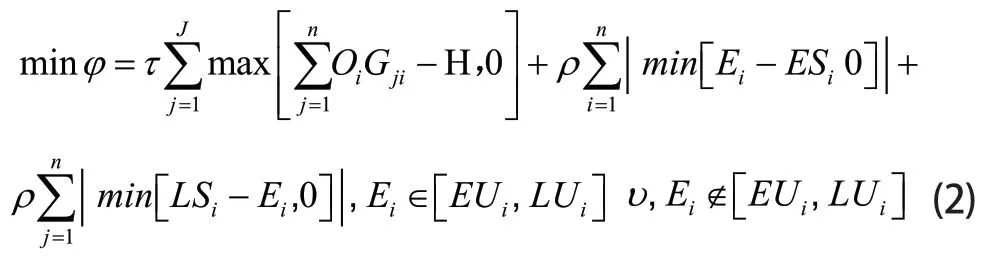
约束条件为：

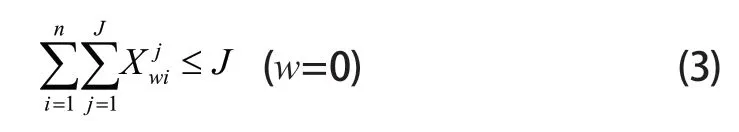
在运行中的AGV小车总数要小于拥有的AGV小车总数

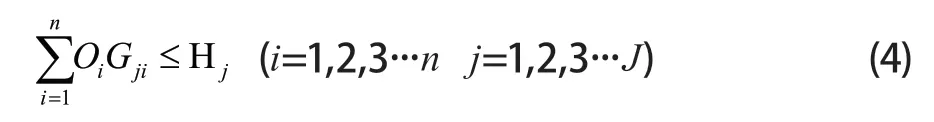
路线中所有货架、货物容量小于AGV小车容量

选择完成车辆

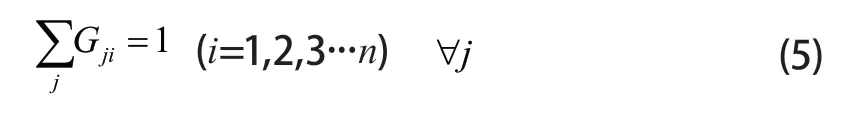
任意车辆下任务w随机

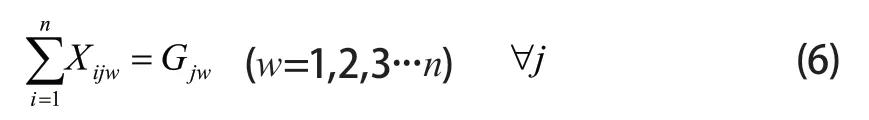
任意车辆下任务i随机

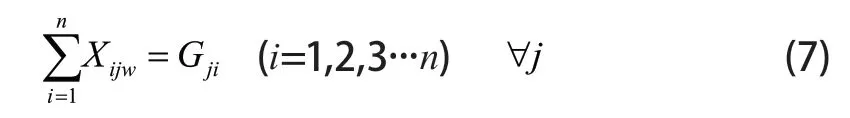
任意车辆下i=0完成任务

任意车辆下路径选择

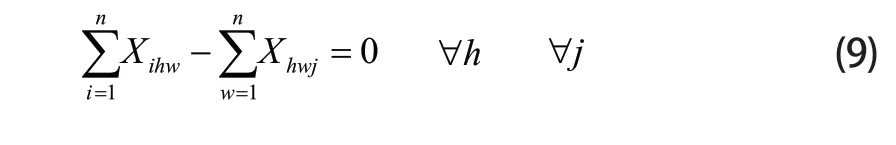
任意车辆下W=0完成任务

任意车辆下AGV满足时间窗需求

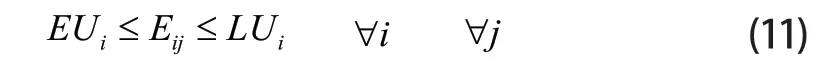
车辆实际到达时间大于货柜需求最早时间小于货柜需求最晚时间

数学模型中的符号说明如下：

φ：目标函数值；

φ1：车辆配送过程中因超载带来的惩罚成本；

φ6：由于配送车辆早到或者延迟带来的时间惩罚成本；

ρ：惩罚系数，其为一个常数；

τ，υ：惩罚系数，认为无穷大的正实数；

Oi：表示第i个货位的需求出库量；

Gji：货位i的任务由配送AGV小车j完成的选择变量；

Hj：AGV小车j的容量；

n：需求货位的总数；

J：拥有的可供配送的AGV小车总数；

：车辆j在路段(Ow O i)上行驶的选择变量；

：AGV车辆j到达客户i的时间；

ESi：任务i期望的最早开始时间；

Ei：AGV小车实际到达任务i的时间；

LSi：任务i期望的最迟开始时间；

EUi：货位能够接受的配送车辆最早卸货时间；

LUi：货位能够接受的配送车辆最晚的卸货时间

2 计算过程及结果

2.1 坐标数据选取

采用Excel软件进行随机选择坐标点数据点在(0，0)至(99，100)之间，如图2所示。设计点(100，50)为出库站台左边点。并且采用Excel软件，在原来随机数据的坐标点上进行随机时间，要求需求起始时间小于终止需求时间，如表1所示。

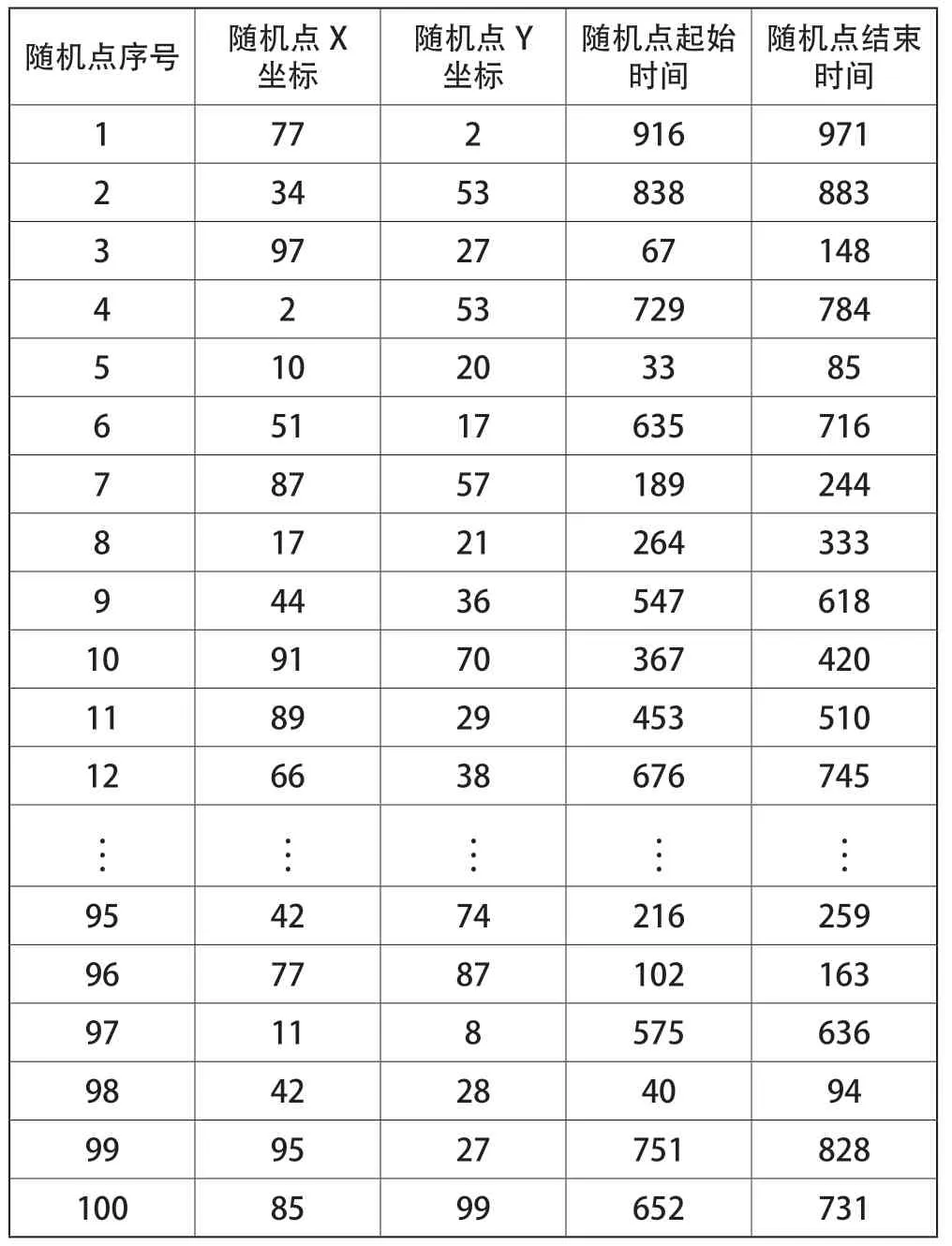
表1 随机点坐标和需求时间短表

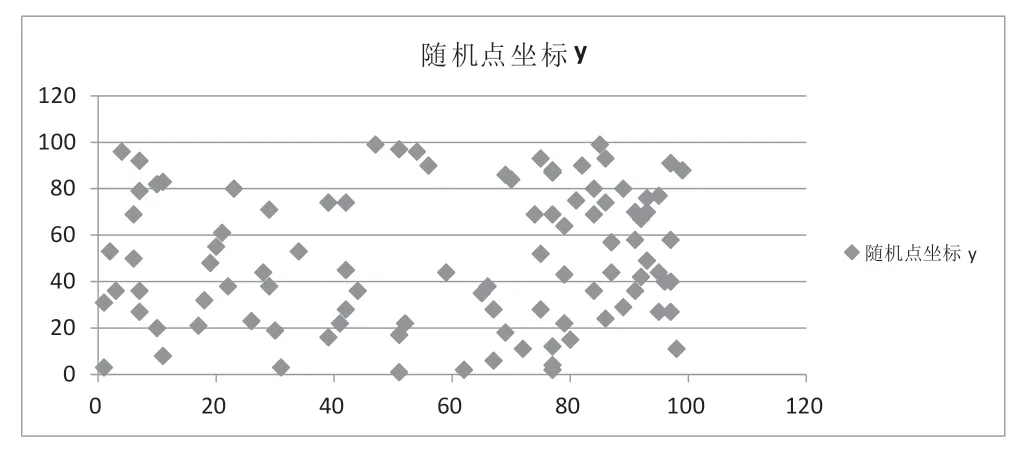
图2 随机点坐标

2.2 Matlab迭代求解

2.2.1 迭代优化

将表1随机点坐标和需求时间短表中的数据代入matlab软件，进行迭代优化，每次迭代的过程逐渐趋于最优值，五十次迭代能够选择出更具代表性和更加优秀的结果，最终得到迭代次数-优化过程图，如图3所示。

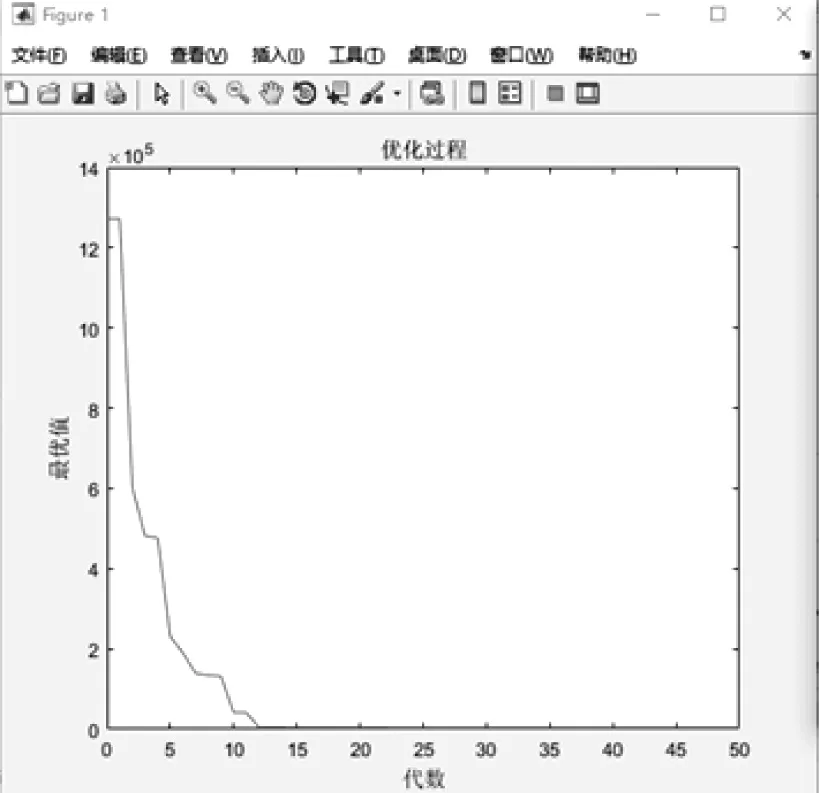
图3 迭代次数-优化过程图

2.2.2 结果求解

对于现代物流中心货物运量增加、货物放置分散，AGV小车固定线路的取货不够精准，无法将加急货物在需求时间内取出，造成AGV小车运输效率低下，我们利用MATLAB软件进行迭代优化，10个不同编号的AGV小车对应着10条不同的运行路线，根据位置坐标AGV从0点即出库月台出发，经由多个不同坐标点，即不同区间的货架最终回到出发点的过程，最终得出最优解是车辆使用数目10辆，车辆行驶总距离2554.8071m。

以下是10辆AGV运行路线表及运行过程图，如表2和图4所示。

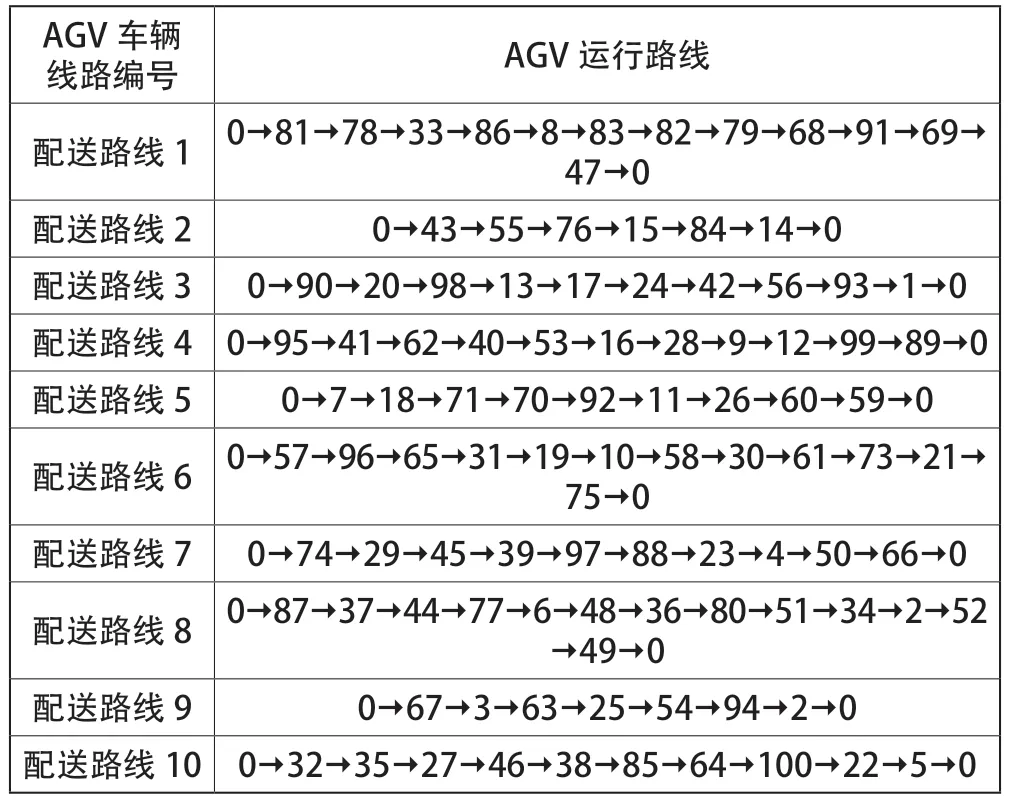
表2 AGV运行路线表

3 结果分析

根据图4 AGV最优方案配送路线图可知，多AGV小车生成了各自的一条运输路线，且每一条运输路线都在约束条件下经由电脑模拟产生，AGV小车由蓝色出库站台点出发，经过不同区间上的货架装载着不同货物，最终回到蓝色出库站台点，该路线符合当时该生产时刻的运载需求，并能够更好地满足运输线路上装载多种商品运输，对比传统的固定线路往返式运输大大降低时间成本，传统的AGV小车在往返式运输线路上空载时以1m/s的速度运行，以表2 AGV运行路线表中的2号车辆运输线路为例，当AGV小车从初始点出发，首先到达43序号点，其位置坐标为(93，76)，装载货物后返回时负载运行速度是0.5m/s，逐一到达该线路其他5个坐标点，完成一组商品的运输总计耗费538.11秒，优化后的运输路线只需将本次运输需要的所有要取得的货物位置坐标输入系统，就会生成多区间、多货架、多品种货物的运输路线图，将2号运输线路的位置坐标输入，生成的运输线路且完成该线路总计用时399.99秒，优化后的路线比传统路线快138.12秒。此外，将剩余的9条运输线路计算并进行对比，最终得出10条运输路线在优化后比原先快了近2.86小时，证实了在时间窗条件下大运量AGV通过算法的优化能够保证最短路径和最优时间进行高效地运行。同时也表明企业要想实现对于一组商品完成快速的出库任务，仅靠传统模式已远远不够，在兼顾效率与成本的前提下多AGV的自主决策路径运输将是推动企业提高效益的关键步骤。

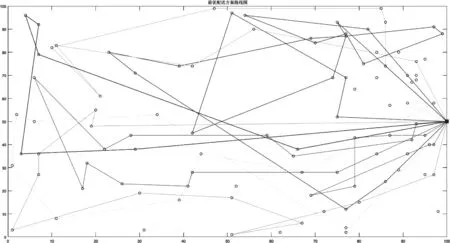
图4 AGV最优配送方案路线图

4 结语

通过对Matlab运行结果的分析，传统的AGV运输路径在运输效率、运输时间方面表现为运输效率低下、用时过长，对传统运输线路进行优化改变了效率低下、用时过长的缺点，并根据其优化结果能更好地调整AGV小车在这些方面的问题，以使效率、时间达到最优化为目标，进而降低了企业的时间成本，时间成本在物流成本中占有很大比重，企业要想获得高额效益，就应尽可能提升货物收发环节的拿取效率。因此，对于路径的规划尤为重要，根据遗传算法模型可知，规划后的AGV小车能在一次路线上运输多个货架的不同货物，对比以往的先进先出式运输方法大大提高了作业效率，这使得企业能够应对不同场景、不同情况下的货物，本文优化结果仅能采用与模拟环境中的仓库模型。具有相同智能货柜和AGV智能小车修改不同货柜位置和仓库环境参数，能够应用于现代智能仓库路径优化方案。AGV小车根据需求时间区间规划路线能够满足急需出库货物的需求，延后不需要急出库货物时间，充分提高了货物流转效率，同时提高了AGV小车的使用效率和企业效益。