基于熵权-Topsis 和非线性规划的企业信贷决策

王建平 张 莉

（东北大学理学院，辽宁 沈阳 110819）

当今世界，中小企业在各国经济发展中占据着十分重要的地位，其在扩大就业、活跃市场、收入分配、社会稳定和国民经济结构布局等方面起着难以替代的作用。然而，中小微企业规模相对较小，发展一直受到资金短缺困扰，银行贷款是其最重要的外部融资渠道。银行通常依据信贷政策、企业交易票据信息和上下游企业影响力，根据各企业的实力、信誉评估其信贷风险，并以此为基础确定是否放贷及贷款额度、利率和期限等信贷策略。

本文通过对123家有信贷记录企业的相关数据、302家无信贷记录企业的相关数据及银行贷款年利率与客户流失率关系的2019年统计数据的处理和分析，分析以下三种情况下中小微企业的信贷风险、贷款利率、贷款额度。

对于有信贷记录情况，首先，在数据预处理及指标分析基础上，采用熵权法确定权重后采用Topsis 法建立企业信贷风险评价模型量化其信贷风险[1]。其次，基于违约金字塔理论[2]，根据各企业信贷风险得到其贷款利率。最后，在得到3种信誉评级下银行贷款年利率与客户流失率关系回归方程基础上，得到各企业客户流失率，并根据RAROC理论[3]建立非线性规划模型，得到年度信贷总额固定时各企业贷款额度。

一、有信贷记录下企业信贷决策

1.数据预处理及指标分析

（1）缺失值、重复值、异常值分析

在实际问题中，可能存在数据缺失、数据重复与数据异常的现象，因此需要对原始数据进行一定的预处理。经判断，所有参考数据均无缺失值、重复值及异常值。

（2）信贷风险评价指标分析

本文对123家企业的信誉评级、违约情况与进项发票和销项发票的发票号码、开票日期、单位代号、金额、税额、价税合计及发票状态的信息按照企业进行初步汇总，得到各企业的信誉相关信息（信誉评级和是否违约）和发票相关信息（进项及销项有效发票、作废发票和负数发票数量及有效金额、有效税额、无效额和有效价税）。

在实际中，银行通常向实力强、供求关系稳定的企业提供贷款，因此，本文从企业实力、供求关系、信誉度3个方面入手进行指标选取。

①企业实力

企业的实力通常由其收入来衡量。收入为销项和进项有效价税的差值，即：

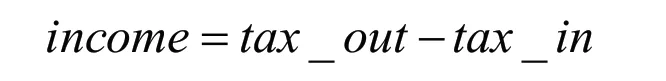
其中，income为收入，tax_in为进项有效价税，tax_out为销项有效价税。

②企业供求关系

企业的供求关系可以通过其供求稳定度衡量。供求稳定度是进稳定度和销稳定度的一个综合指标，按如下公式计算：

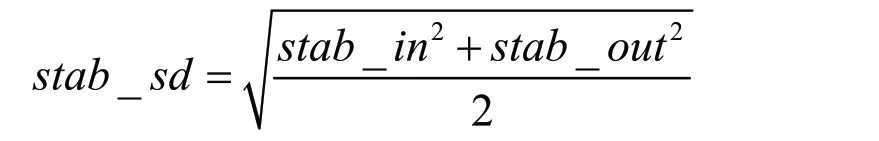
其中，stab_in为进稳定度，stab_out为销稳定度，stab_sd为供求稳定度。

进稳定度可以通过稳定销方发票数在总进项发票数中的占比衡量。同理，销稳定度可以通过稳定购方发票数在总销项发票数中的占比衡量。即：

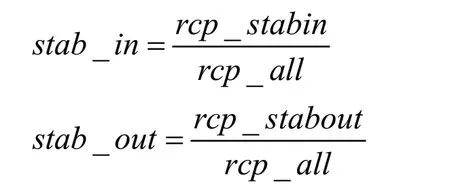
其中，rcp_stabin为稳定销方发票数，rcp_stabout为稳定购方发票数，rcp_all为总发票数。“稳定销方（购方）”取进项（销项）发票数排名前3位的销方（购方）。

③企业信誉度

企业的信誉可以由其信誉评级、违约情况、作废发票率和负数发票率反映。其中，信誉评级和是否违约为原始指标，作废发票率和负数发票率按如下公式计算：

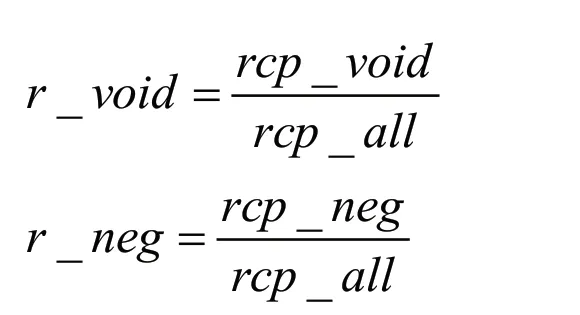
其中，r_void为作废发票率，r_neg为负数发票率，rcp_void为作废发票数，rcp_neg为负数发票数。综上，本文选取用于评估企业信贷风险的3个方面的6个指标，3个方面分别为企业实力、供求关系和信誉度，6个指标分别为收入、供求稳定度、信誉评级、是否违约、作废发票率、负数发票率。

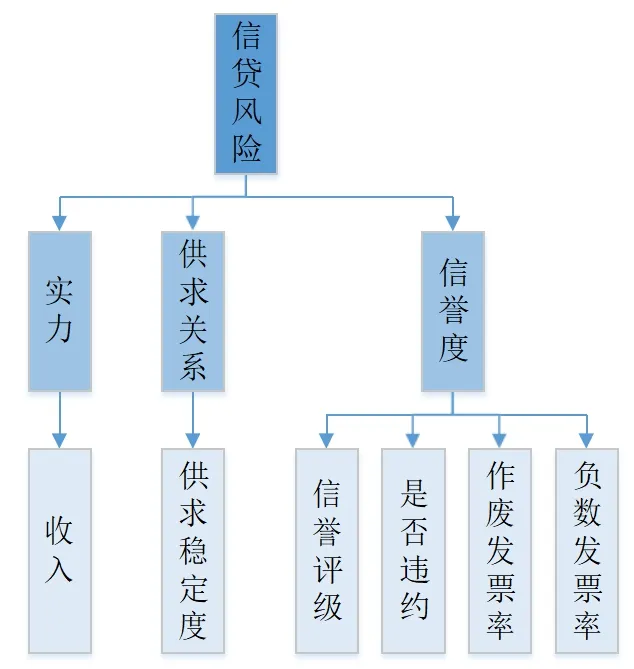
图1 企业信贷风险评价指标体系

2.熵权-Topsis法信贷风险量化模型

（1）定性指标量化处理

信誉评级指标是定性指标，本文通过构造偏大型柯西分布隶属函数，对其进行量化处理。偏大型柯西分布隶属函数[4]：

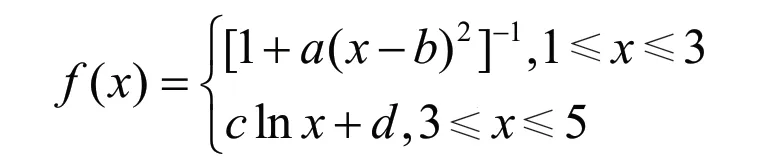
其中，α，β，a，b为待定系数。对于信誉评级指标，评语集为{A，B，C，D}，设其对应取值为5、4、3、2。规定信誉评级为A时隶属度为1，即f（5）=1；信誉评级为B时隶属度为3，即f（3）=0.8；信誉评级为D时，隶属度为0.01。经计算得α=1.1086，β=0.8942，a=0.3915，b=0.3699。将其代入上式可得f（4）=0.9126，f（2）=0.5245。故信誉评级指标量化值分别为{1，0.9126，0.8，0.5245}。

是否违约指标原始取值为“是”“否”，本文将其用0-1指标进行量化，“是”量化为1，“是”量化为0。

（2）熵权法确定权重

熵权法是一种客观赋权方法，可以最大程度避免主观赋权对信贷风险量化结果的影响，基本思路是根据指标变异性的大小来确定客观权重，指标的变异程度越小，所反映的信息量也越少，其对应的权值也应该越低。

①数据正向化和标准化处理

设有n个企业，m个评价指标，则xij为第i个企业的第j个指标的数值（i=1，…，n；j=1，…，m）。

由于本文选取的各项指标计量单位并不统一，因此需要进行标准化处理。而正向指标（如收入、供求稳定度等指标）和负向指标（如作废发票率、负数发票率等指标）的含义不同，对于正向和负向指标需要采用不同的算法进行处理。

对于正向指标：

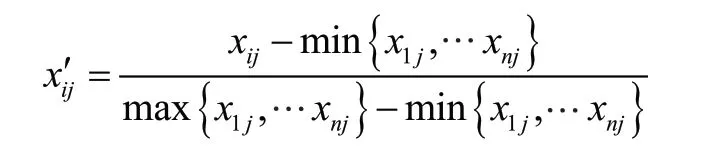
对于负向指标：

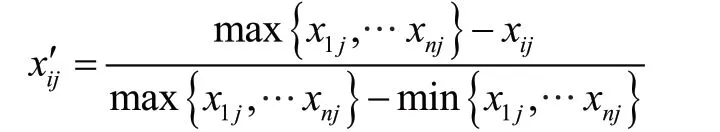
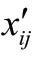
②计算各指标下第i个企业权重将权重看作计算信息熵时的概率：

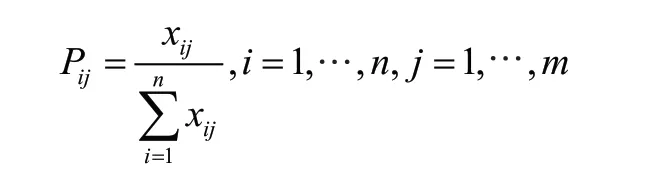
③算各指标信息熵及信息效用值对于第j个指标，其信息熵为：

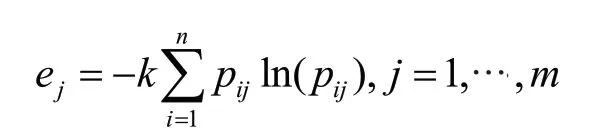
其中，

对于每个指标，其信息熵越大则对应信息量越小。

因此，引入信息效用值以正向衡量信息量：

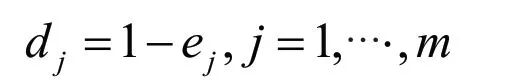
④计算各指标权重

将各指标的信息效用值归一化，得到每个指标的熵权。

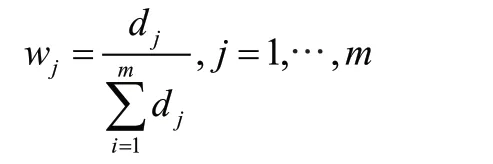
表1 信贷风险评价指标权重

（3）Topsis法量化信贷风险

Topsis法是根据各企业数据构造一个理想化目标（即信贷风险最低企业），然后衡量各企业与该理想化企业的相对接近程度，越接近代表其信贷风险越低。

①数据标准化处理

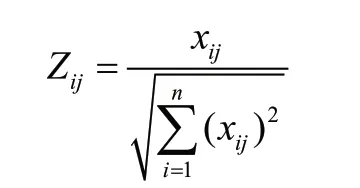
由此得到标准化处理后矩阵：

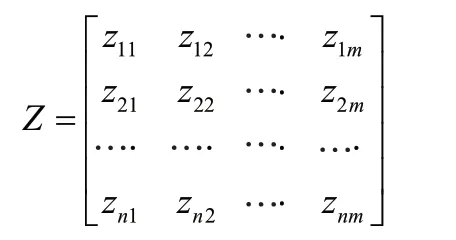
②确定最优方案和最劣方案

最优方案Z+由Z每列最大值构成，即：

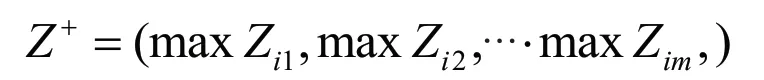
最劣方案Z-由Z每列最小值构成，即：

③计算各样本与Z+和Z-的距离

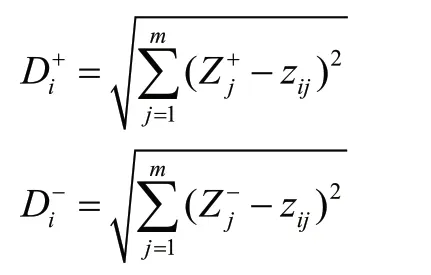
④计算各样本综合得分

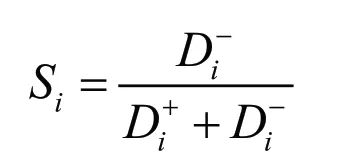
可以看出，各企业的综合得分值Si在[0，1]范围内，且可以反向反映其信贷风险。Si越大，该企业信贷风险越低；Si越小，该企业信贷风险越高。将该负向指标正向化，得到企业信贷风险指标。

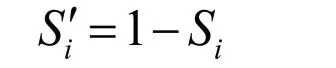
根据上述方法，得到123家企业的信贷风险量化分析结果，由于篇幅限制，此处仅展示前5家企业的信贷风险。

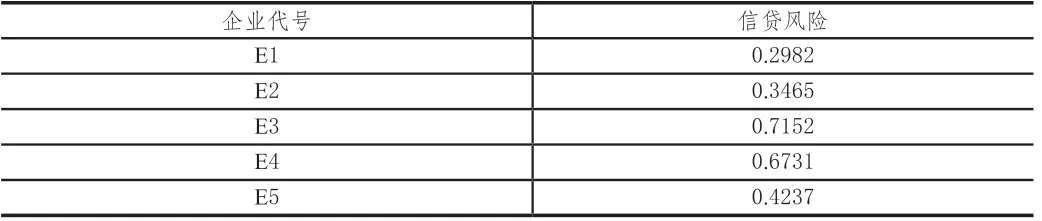
表2 有信贷记录前5家企业信贷风险

3.RARAC-非线性规划信贷策略模型

首先，得到有信贷记录的123家企业信誉评级分布情况（如图2所示）。

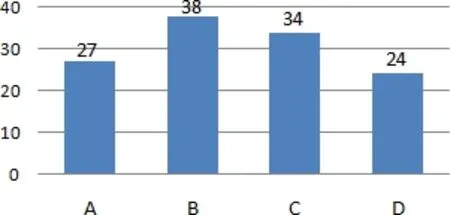
图2 123家企业信誉评级分布情况

由于银行对信誉评级为D的企业原则上不予放贷，下文确定信贷策略时删除24家信誉评级为D的企业，仅分析其余99家企业的信贷策略。

（1）贷款利率确定

根据违约金字塔理论，银行发放贷款在追求盈利的同时需要保证安全性，在确定贷款利率时，需要保证信贷风险越低的企业，其贷款利率也越低。根据经验，可按照如下公式确定各企业的贷款利率。

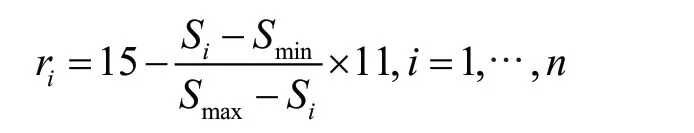
由于确定贷款额度的模型中需要客户流失率指标，本文根据银行贷款年利率与客户流失率统计数据，绘制客户流失率-利率关系曲线图（如图3所示）。

图3 客户流失率-银行贷款利率关系曲线图

由图3，分别建立二次、三次模型和对数模型进行曲线拟合，经分析，三次模型拟合效果最好，故选择该模型，得到不同信誉评级的客户流失率（l）-利率（r）关系表达式为：

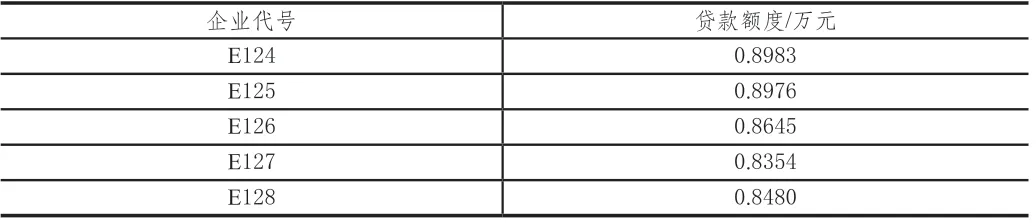
表 6 无信贷记录前5家企业信贷风险

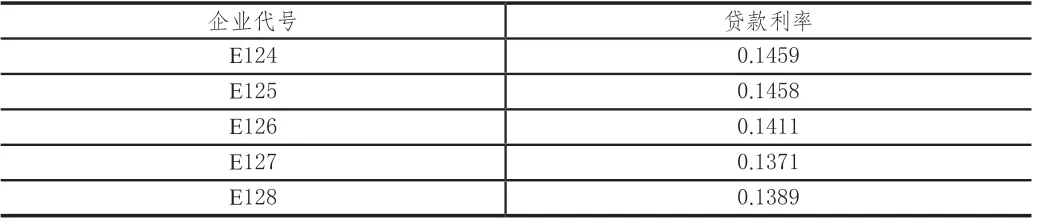
表 7 无信贷记录前5家企业贷款利率

对于信誉评级A：

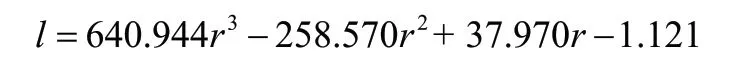
对于信誉评级B：

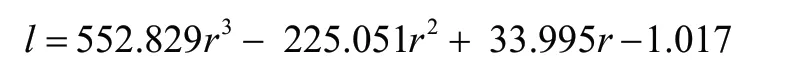
对于信誉评级C：

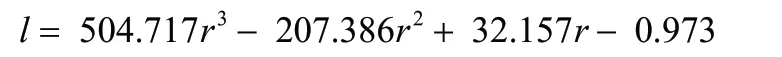
根据以上模型，得到99家企业的贷款利率及对应银行客户流失率。

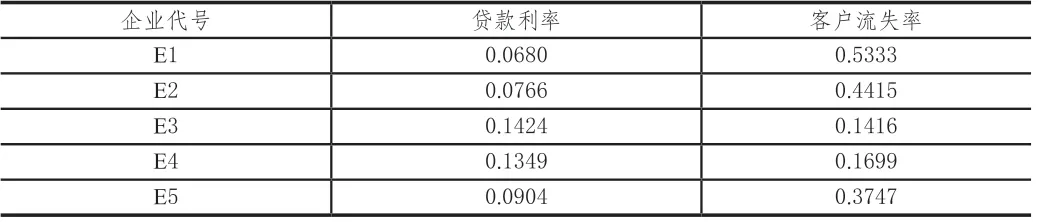
表3 有信贷记录前5家企业贷款利率和客户流失率

（2）贷款额度确定

本文选择建立基于RAROC理论的非线性规划模型确定贷款额度，其目标函数和约束条件按照如下方法确定。

①目标函数

银行经营者在确定信贷决策时，需要从风险和收益的双重角度考虑，即期望达到风险最小化和收益最大化两个目标。RAROC模型是当今银行用于贷款风险定价的核心技术手段，明确了风险控制对商业银行经营效率的影响，目标是将风险调整后的收益最大化，即：

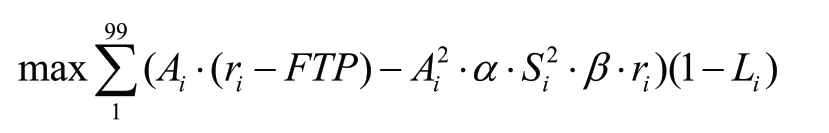
通过查阅相关资料，上述公式中系数取值分别为：

②约束条件

由于该银行对确定要放贷企业的贷款额度为10～100万元，故约束条件为：

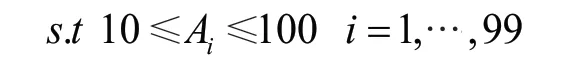
综上，非线性规划模型为：

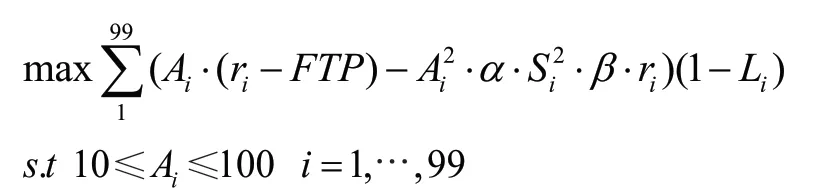
根据以上模型，得到99家企业的贷款额度。

表4 有信贷记录前5家企业贷款额度

二、无信贷记录下企业信贷决策

为了解决无信贷记录企业信贷决策问题，本文将其转化为有信贷记录的信贷决策问题处理。

1.是否违约和信誉评级指标预测

无信贷记录数据与有信贷数据相比缺少是否违约和信誉评级指标的数据，因此需要对各企业的是否违约和信誉评级指标进行预测。本文在123条有信贷记录数据中随机选择80%作为训练集，20%作为测试集，分别训练SVM和MLP模型，然后对302家企业预测是否违约和信誉评级指标。

（1）是否违约预测

是否违约指标是0-1型指标，对其进行预测可视为小样本、非线性二分类问题。SVM在解决小样本、非线性及高维模式问题中成效显著。其主要思想为通过自主学习找到分类效能较出色的支持向量，然后将这些向量映射到高维空间并在该空间建立一个将样本正确分类且间隔最大的超平面，具体步骤如下。

①输入训练集

②基于最小训练误差求最大分类间隔

③求解分离超平面

④分类决策

（2）信誉评级预测

信誉评级指标取值为A，B，C，D，对该指标进行预测可视为多分类问题。本文采用MLP解决该问题。MLP是一种前馈人工神经网络模型，主要包含输入层、输出层及若干隐藏层。为了增加模型的非线性，加入激活函数对每一层进行非线性变换。

①前向传播

②反向传播

本文按照上述方法，经过正向传播和反向传播，不断更新MLP参数，输出各企业信誉评级预测值。综合以上模型，得到无信贷记录302家企业的信誉评级和是否违约指标的预测值。

表5 前5家企业信誉评级和是否违约指标预测

2.信贷风险量化及信贷策略分析

由于银行对信誉评级为D的企业原则上不予放贷，下文确定信贷策略时删除49家信誉评级预测为D的企业，仅分析其余253家企业的信贷策略。

综上预测了各企业是否违约和信誉评级指标，将无信贷记录的情况转化为有信贷记录的情况。因此，首先按照有信贷记录情况的方法对数据进行预处理并计算指标值。然后利用有信贷记录情况下信贷风险评价模型和贷款利率模型得到各企业的信贷风险和贷款利率。

三、结论

本文建立了有/无信贷记录及突发事件影响下中小微企业的熵权-Topsis法信贷风险量化模型和RAROC-非线性规划信贷策略模型。

（1）熵权-Topsis法信贷风险模型将信贷风险的多方面影响因素归纳为3个方面的6个指标，建立了科学的信贷风险评价指标体系，通过熵权法客观赋权避免了主观性。

（2）RAROC-非线性规划信贷策略模型以RAROC理论为支撑，该理论不仅考虑了企业的信贷风险，也考虑了潜在客户流失可能造成的损失，从风险和收益两方面共同分析，使模型具有充分的理论依据。