源头数据治理视角下中小企业信贷三方主体博弈分析

王艳萍 赵华伟

（齐鲁工业大学经济与管理学部金融学院，山东济南 250100）

一 、引言

在数字化转型的当下，数据作为重要的生产要素，是金融市场中必不可少的参考依据，是各企业实现效益最大化的重要资产，其质量对于有效开展金融业务及释放价值而言举足轻重，具体来看，高质量的金融数据还可为预测金融风险建立警示报警系统，可降低众多风险影响，譬如信贷风险、运营风险等（Korhonen JJ等，2013；Emieux V等 ，2014；Putro B L等，2016）。针对数据的海量增长及重要性的凸显，数据有效治理问题应运而生，其中源头数据治理则是重要的组成部分，若源头数据为假，数据的分析与处理则变得毫无意义（夏诗园等，2022）。

在信贷市场中，中小企业用于贷款的数据资料，是对企业进行精准分析的源头数据。从微观角度来看，该数据关系到企业发展过程中的融资成本问题，从宏观角度来看，它可以影响金融机构对于单个企业乃至整个行业的判断，最终对金融政策的制定及实施产生影响。因此为实现信贷市场的健康有序发展，避免系统性风险的发生，源头数据治理势在必行。

有关数据治理学者们多从立法、管理及技术角度展开论述数据治理的重要性及必要性，且对国际及国内数据共享障碍、安全流通关注度较高（李涛，2022；王伟玲，2022）。针对中小企业在信贷市场中的行为，更多从其是否能够偿还贷款角度出发，抛出了“不管黑猫白猫，抓住耗子就算好猫”的问题。但分析看来，引入第三方机构，譬如政策性担保机构、第三方物流企业等防止中小企业无法偿还贷款，却出现其与中小企业合谋,最终导致银行及公众利益受损的情况，究其根源依旧是数据造假问题（马松等，2015；祝拥军等，2013）。不可否认，中小企业、信贷审批员以及监管代理人员三方的不作为及合谋行为导致流入信贷市场中的底层资产相关数据造假、未实现穿透式监管等问题时有发生。因此，本文在银保监会将银行监管统计纳入数据治理范畴计划的背景下，考虑源头数据治理问题，从审查中小企业提交的信贷资料角度出发，结合银行信贷审批人员以及监管代理人员工作合规性两因素，构建中小企业、信贷审批人员以及监管代理人员三方博弈模型，致力于为政府、监管部门对于银行监管统计数据以及流入金融市场的中小企业数据的源头治理提供借鉴意义。

二、博弈模型构建

（一）问题描述和基本假设

信贷市场中源头数据治理相关三方的策略选择如下：中小企业策略空间为（提供真实数据，提供虚假数据）；信贷审批人员策略空间为（合规审核放贷，违规审核放贷），违规审核放贷表现为信贷审批人员的合谋以及不作为；监管代理人员的策略选择为（合规监管，违规监管），其中，违规监管可理解为合谋行为以及不作为。以上三方都属于有限理性人，即在实际信贷业务的过程中，他们会通过其他主体的行为变化而调整改变自己的策略，整个信贷业务的博弈结果会由此发生变化，最终趋向于某一稳定状态，可见，以上博弈过程符合演化博弈特征，因此，本文基于演化博弈理论对源头数据治理过程中的中小企业、信贷审批人员及监管代理人员的行为进行分析。

（二）确定模型参数

为构建博弈模型，对各参与方策略及其稳定性展开分析，做如下四点假设：

假设1 中小企业获得贷款后收益为Pe，中小企业提供真实数据的成本为Cet，提供虚假数据的成本为Cef,而中小企业提供虚假数据的成本主要包括伪造虚假企业数据、虚假宣传以及贿赂信贷审批人员等进行意向合谋行为所涉及的经营管理费用。中小企业提供真实数据获取收益Pe的概率为a;中小企业提供虚假数据，其获取贷款的可能性取决于银行审核，若获得贷款，假设其获取收益Pe的概率为b（a>b）；中小企业信贷业务提供虚假数据将面临罚金等惩罚，设为De,而提供真实数据将获得优惠利率等奖励，设为Be。

假设2 信贷审批人员合规审核以及违规审核放贷的成本分别为Cbl、Cbi（Cbl>Cbi），且审批业务收益为Ib。若审批人员严格审核，审批人员百分百可获得此笔业务收益，同时可获得业务奖金激励Bb；反之，审批人员不作为导致业务漏洞而遭到惩罚为Db1；审批人员的合谋行为，会额外收受贿赂，设为Be，从而招致惩罚设为 Db2，Db2> Db1。

假设3 监管代理人员合规监管与违规监管成本为Css、Clr，监管业务收益为Is；监管代理人员选择不作为，无从获得中小企业和信贷审批人员的策略选择，因此对其两者策略均不设奖惩，而其本人将受到监管部门的惩罚Fs1；当监管代理人员合规监管时，设其百分百会发现信贷业务中的合谋现象；若监管代理人员选择合谋，在收受贿赂Bs的同时还会受到监管部门的惩罚Fs2；监管代理人员合规监管获得奖金等正向激励，设为Bss。

假设4 中小企业选择提供真实数据策略的概率是x，提供虚假数据策略的概率则为（1-x）；信贷审批人员选择严格审核放贷策略的概率是y，违规审核放贷策略的概率为（1-y）；监管代理人员选择合规监管策略的概率是z，反之，则为（1-z），且x,y,z∈[0,1]。

（三）构建收益矩阵

根据上述分析和假设，中小企业、信贷审批人员及监管代理人员在不同的策略组合下的支付矩阵如表1所示。

表1 中小企业、信贷审批人员和监管代理人员演化博弈支付矩阵

三、三方主体演化博弈行为均衡分析

（一）博弈三方的期望收益和平均收益

设UA1为中小企业提供真实数据时的期望收益，UA2为提供虚假数据时的期望收益，UA为中小企业的平均收益，则：

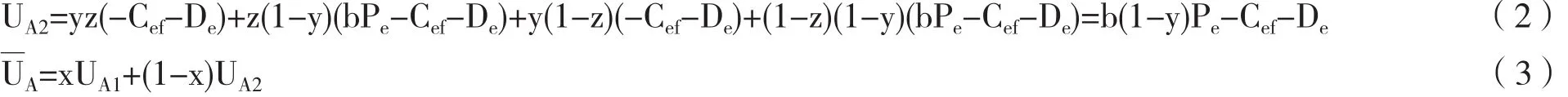
原理同上，设UB1表示信贷审批人员合规审核放贷时的期望收益，UB2表示违规审核放贷时的期望收益，示信贷审批人员的平均收益，UC1、UC2、别代表监管代理人员合规监管时的期望收益、违规监管时的期望收益以及其平均收益。

（二）三方主体的复制动态方程和演化稳定性分析

1.基于复制动态方程原理，根据式（1）和（2）可构造中小企业选择提供真实数据策略时的复制动态方程F（x）

当y=[Cet-Cef-De-Be1+(b-a)Pe]/bPe时，F(x)恒为零，此情形代表了，无论中小企业提供真实数据的概率为何，系统均处于稳定状态。当y≠[Cet-Cef-De-Be1+(b-a)Pe]/bPe时，令F(x)=0,得到x=0,x=1两个稳定点。而均衡点为稳定策略需要满足其导数小于零的条件。因此，当y<[Cet-Cef-De-Be1+(b-a)Pe]/bPe时，F′(0)<0，F′(1)>0，故x=0为稳定策略。而当条件相反时，x=1为稳定策略。中小企业策略演化相位图，如图1（a）所示，其中，中小企业提供虚假数据的概率为VA1，提供真实数据的概率为VA2。

2.根据UB1和UB2可构造信贷审批人员选择合规审核放贷策略的复制动态方程F（y）。

当x=(Cb1-Bb-Cbi-Be2-Db2)/(Be2-Db2+Db1)时，F(y)≡0，此时无论y为何值，其均处于稳定状态。当x≠(Cb1-Bb-Cbi-Be2-Db2)/(Be2-Db2+Db1)时，令F(y)=0，得到y=0，y=1两个稳定点。同理可得，信贷审批人员的策略演化相位图，如图1（b）所示， VB1为信贷审批人员稳定选择违规审核放贷的概率，VB2为稳定选择合规审核放贷的概率。

3.根据UC1和UC2可构造监管代理人员选择合规监管策略的复制动态方程F（z）。

当y=[Css-Bss+Clr-xFs1+(1-x)(Bs-Fs2)]/[(1-x)(Fs1+Bs-Fs2)]时，F(z)恒为零，z取何值，其状态均为稳定。而当y≠[Css-Bss+Clr-xFs1+(1-x)(Bs-Fs2)]/[(1-x)(Fs1+Bs-Fs2)]时，令F(z)=0,得到0和1两个稳定点。同理可得，监管代理人员的策略演化相位图，如图1（c）所示。其中，VC1表示监管代理人员违规监管的概率，VC2表示合规监管的概率。

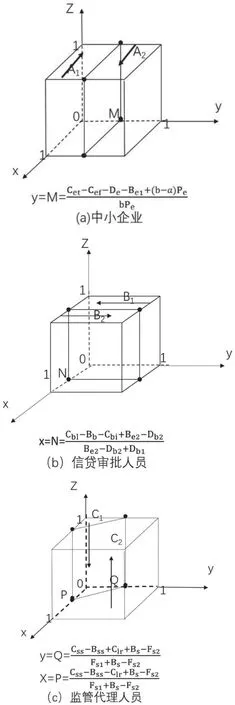
图1 三方主体动态趋势相位图

（三）三方演化博弈系统均衡点的稳定性分析

由F（x）=0,F(y)=0，F（z）=0可得系统均衡点：E1（0，0，0）、E2（0，0，1）、E3（0，1，0）、E4（0，1，1）、E5（1，0，0）、E6（1，0，1）、E7（1，1，0）、E8（1，1，1）及混合策略纳什均衡解。卢超等（2020）学者指出，处于稳定状态的均衡点，不仅要满足严格纳什均衡的条件，还要满足纯策略纳什均衡的条件。因此，本文不会再将混合策略纳什均衡考虑在内，也不再展开分析。而后，通过分析系统雅可比矩阵的特征值，判断系统在以上8个特殊均衡点处的稳定性。分别对F(x)、F(y)、F(z)中的x、y、z求偏导得到雅可比矩阵。当矩阵J所有特征值均为负数的条件满足时，博弈系统的均衡点才是稳定的（邓建高等，2021）。E1-E8对应的雅可比矩阵的特征值如表2所示：

表2 E1-E8对应的雅可比矩阵的特征值

由表2中的特征值表达式，以及各参数的取值范围，各平衡点稳定性讨论如下：

因为中小企业提供真实数据的收益aPe+Be1-Cet>0恒成立,所以E3、E5为不稳定点。

情形1-1：-A<0 恒成立，此时，若-Bb+Cb1-Cbi-Db1<0且Bss-Css+Clr+Fs1<0成立，则表示信贷审批人员不作为的支出大于合规审核的支出（条件一），且监管代理人员合规监管得益大于不作为监管支出成立时，只有E7为演化稳定点。一方面，在信贷过程中，中小企业在数据真实性问题上自发达到了较高水平，另一方面，信贷审批人员合规业务操作，为保障信贷市场整体数据的真实性营造了较好的环境，从而有助于实现数据治理的正本清源；

情形1-2：若-Bb+Cb1-Cbi-Db1<0且Css-Bss-Clr-Fs1<0成立，代表满足条件一，且不作为监管支出大于监管代理人员合规监管成本与激励之差时，只有E8为演化均衡点。这时中小企业规范的信贷行为为金融市场提供真实的企业数据、信贷审批人员合规审核，监管代理人员合规监管，三方主体的策略达到最优。

情形2-1：当（a-b）Pe+Be1-Cet+Cef+De<0且Bb-Cbl-Be2+Db2+Cbi<0时，若同时满足Bss-Css+Clr-Bs+Fs2<0,表示中小企业提供真实数据成本与提供真假数据获得贷款后收益的差值之差大于提供虚假数据支出（条件二）、信贷审批人员合规审核的收益小于合谋审核的收益（条件三）且监管代理人员严格审核得益小于合谋监管得益时， E1满足条件，为演化稳定点，这时虚假数据泛滥，信贷审批人员及监管代理人员的合谋行为，不利于整个金融市场健康有序发展，必将导致数据治理出现漏洞，导致金融市场出现大的危机；

情形2-2：若同时满足Css-Bss-Clr+Bs-Fs2<0，则表示在条件二、条件三且监管代理人员合规监管收益大于合谋监管惩罚情况下，点E2为演化稳定点，此时，虽然监管代理人员业务操作规范，但源头数据治理目标并未实现，因此，要阻止这一情形的发生。

情形3-1：当（b-a）Pe-Be1+Cet-Cef-De<0且Bb-Cbl+Cbi+Db1<0时，若同时满足Bss-Css+Clr+Fs1<0,表示中小企业满足提供真实数据成本和提供真假数据获得贷款后收益的差值之差小于提供虚假数据支出（条件四）、信贷审批人员同时满足合规审核支出大于不作为审批支出（条件五）、监管代理人员同时满足合规监管支出大于不作为监管支出情形时，点E4演化稳定点，此时中小企业依靠自身的道德约束及社会责任感提供真实数据，通过正规渠道获得贷款及收益，而此时信贷审批人员与监管代理人员在工作中处于不作为状态，一旦中小企业受到整个信贷业务流程操作不规范的影响，产生提供虚假数据的可能性，必将对数据治理产生致命的影响；

情形3-2：若同时满足Css-Bss-Clr-Fs1<0,则表示在条件四、条件五且监管代理人员合规监管支出小于不作为监管支出情形下，点E6为演化稳定点，此时信贷市场中中小企业选择提供真实数据，中小企业自身道德约束及社会责任感较强，便于实现源头数据治理，而信贷审批人员选择不作为，监管代理人员选择合规监管。考虑到，信贷审批人员的不作为在数据治理过程中可能造成较大事故，因此这种情形应该被避免。

四、结论及对策建议

针对信贷过程中的合谋及不作为等行为，本文构建中小企业、信贷审批人员以及监管代理人员的三方演化博弈模型，分析三者各自策略选择的稳定条件以及三方整体策略稳定条件，得出中小企业相关三方最优策略组合E8（1，1，1）发生的条件，并从各参数角度出发，结合第三部分各情形为信贷市场源头数据治理提出如下对策与建议：

第一，政府应加大奖惩力度，简化信贷审批及监管流程，降低过程成本，推动三方主体各司其职，实现源头数据治理，提高信贷市场乃至金融市场中的数据质量；

第二，政府及各部门应为中小企业营造良好的运营环境，为中小企业保驾护航，提高其获利的可能性，激励中小企业通过正规操作以及真实企业数据获得信贷支持，避免其产生数据造假的想法。

第三，金融机构及监管机构应充分利用大数据平台，提高中小企业数据造假成本，以及各部门工作人员违规成本，防止中小企业提供虚假数据。与监管代理人员相比，源头数据质量与信贷审批人员所营造的信贷环境表现出强相关，因此，为减少信贷市场中的虚假数据，监管部门在关注监管代理人员是否严格监管之时，更应该加强信贷审批人员的管理。

第四，源头数据治理关键在于数据源头。中小企业提供的数据质量与其自身的道德约束及其社会素养有关，因此要加强企业信用体系建设，在中小企业方面扩大诚信的宣传。

本文考虑了中小企业提供虚假数据所需的投机成本以及寻租成本，但并未将其单独作为参数分析。因此，单独考虑寻租成本以及造假成本对于虚假数据出现的概率影响，可能是下一步努力的方向。