房产税改革与房价波动
——基于动态面板数据模型的研究
刘 璐 石 慧
(中国人民银行长春中心支行,吉林长春 130051;中国人民银行白城市中心支行,吉林白城 137000)
一、引言
近二十年来,我国的房地产市场经历了高速发展。在过去的十年中,我国主要城市房地产价格翻了几番,有的地方甚至达到10倍左右。这种现象在“北上广深”等一线城市的黄金地段尤其明显。为了抑制房地产市场过热房价过快上涨,从中央到地方推出了一系列限贷、限购、限价等调控政策和措施,基本遏制住了房价快速攀升的势头,但房价总体仍处于高位。2010年,中国政府网发布的《国务院批转发展改革委关于2010年深化经济体制改革重点工作意见的通知》(国发【2010】15号)中首次提出“逐步推进房产税改革”,2011年1月28日,上海、重庆两市率先启动了个人住房房产税改革试点工作,从此拉开了我国房产税改革的序幕。近年来随着房地产业的持续升温,房产价格波动和房产税改革问题成为研究讨论的焦点。中国的房产税对房价波动的影响作用如何?影响机理是什么?本文将试图分析和解释这些问题。
二、房产税改革国内外研究现状
从国外研究来看,Katrina Lewiston(2001)从房地产行业的特点出发,依据房地产行业的特点对纳税进行分析,创新性地提出用博弈论方法研究纳税问题。David M.S(2007)做了大量的调查研究分析了美国房地产市场发现,税收优惠政策会影响房地产市场的发展。Niels Johannesen(2010)认为房地产项目在建设过程中会受到当地税收政策的影响,因此要充分考虑当地公众利益去进行纳税。Gina L DeRosa(2016)在对以往的研究分析发现,房地产行业对于税收政策的敏感度较高,销售价格会随着税收政策的变化而变化,充分了解税收政策有利于房地产企业提高销售量。
从国内研究来看,戚克梅(2013)指出房地产具有私人商品和公共商品的“双重属性”。崔光灿(2018)也同样阐述了住房是兼具社会属性和经济属性的“双重属性”的结合体。李成和于海东(2020)发现住房按揭贷款会放大经济政策不确定性对消费的负面作用,受新冠疫情影响居民的预防性储蓄增加,消费倾向降低。伍文中和李燕(2021)通过实证研究发现商业银行的资本充足率、总资产收益率、资产负债率以及货币供应量等因素与我国房价正相关,而利率与房价呈负相关。邹士年(2022)从国房景气指数、投资销售面积等方面分析房地产行业的业务收缩现状。
三、基于动态面板模型的实证分析
通过上文的分析,基本确定了房产税抑制房价波动的作用。接下来,我们需要构建一个计量模型,选择合适的数据指标,对以上结论进行实证检验。实证分析采用的是动态面板数据模型差分GMM和系统GMM估计方法。
(一)模型构建与数据统计分析
首先,构建房产税影响房价波动的计量模型。由于房价波动具有较强的自相关效应,所以本章构建的计量模型将房价的滞后项也纳入到解释变量中来。具体的计量模型为:
其次,对计量模型中的关键变量选择合适的数据指标,本文采用的数据是中国31个省市区的面板数据,所有数据都经过GDP平减指数进行了真实化处理。由于我国目前房产税征收的主要对象是商业用房,因此,这里的房价数据分别选取了全国各省市地区的商业营业用房平均销售价格(y)、商品住宅平均销售价格(y1)、商品房销售平均价格(y2),时间跨度为1999-2020年。房产税税率指标主要是用全国各省每年征收的房产税(x1)、耕地占用税(x2)除以商品房销售额,时间跨度同样从1999-2020年。
表2为各项指标的描述性统计分析结果。从结果可以看出,房价波动与房产税税率之间呈负相关关系,相关系数分别为-0.3478、-0.2677、-0.3406、-0.3125、-0.3421、-0.3154,这说明房产税税率从统计分析的角度来看与房价波动的变动趋势相反,大概可以推断房产税税率具有抑制房价波动的作用。

表2 各项指标的描述性统计结果
(二)模型估计
Blundell,Bond(1998)提出的系统广义矩估计方法(以下简称SYS-GMM估计)与Arellano,Bond(1991)提出的差分广义矩估计方法相比,可以在有效减轻内生性问题以及残差异方差性的同时,提高估计效率,在实证检验中得到广泛的应用。本文为了确保模型估计的有效性和稳健性,同时进行了差分广义矩估计和系统广义矩估计两种方法进行回归。此外,在使用系统广义矩估计方法进行实证分析时,需要进行两个重要的检验:过度识别检验和干扰项序列相关检验。其一,过度识别检验需要采用Sargan检验判断工具变量的使用是否合理,该检验的原假设为工具变量使用合理;其二,干扰项序列相关检验需采用Hansen检验,其原假设是不存在序列相关。Hansen检验要求一阶序列相关,二阶不相关,即一阶检验拒绝原假设,二阶检验接受原假设。
在具体实践过程中,为了全面考察房产税改革政策推出前后的变化和影响,本文还分别对不同时间段和不同地区进行分别回归。考虑到2011年我国开始实施房产税试点改革,因此,在2011年前后,房产税对房价的影响可能会受到改革的冲击而发生变化,因而我们将1999-2010年划为一个时间段,将2011-2020划为另一个时间段进行分别回归分析。在对比不同区域时,主要是将全国31个省区市划分成东、中、西三大区域进行分别回归。
根据表3可知,回归结果既通过了自相关检验,也通过了Hansen和Sargan检验,说明结果较为理想。通过筛选,最终选定房价波动的一阶滞后项作为解释变量,同时在具体回归过程中,考虑到房产税税率与房价波动之间可能存在的内生性问题,进而降房产税税率设定为模型的内生变量进行一阶差分和系统广义矩估计。下面对回归结果的系数进行具体分析。

表3 全时段、房产税改革前后分时段回归结果汇总表
首先,全时段的回归结果分析。根据表3可知,普通最小二乘法、固定效应模型、一阶差分矩估计和系统广义矩估计模型中,房价波动滞后一期的估计系数为正,系数大小分别为0.870、0.710、0.575和0.860,且高度显著,这说明上一期房价波动每增加1%,本期房价波动就会增加0.860%(系统广义矩估计sGMM估计结果,下文分析重点对比一阶差分矩估计和系统广义矩估计模型,普通最小二乘和固定效应模型仅作为参考,不再赘述),说明房价波动具有自我调节的正向反馈效应。房产税税率的估计系数为负。sGMM模型估计系数为-0.017,均在1%的水平上显著,这意味着房产税税率提高1%,本期房价波动就会减少0.017%。这说明房产税对房价波动具有抑制作用。房贷利率估计系数为负,人均GDP增长率估计系数为正,说明利率与房价波动负相关,对房价产生抑制作用,人均GDP增长率与房价波动正相关,会加剧房价波动。
其次,分析房产税试点改革前后的回归结果。根据表3中(4)sGMM估计结果可知,房价波动的滞后一期在房产税改革试点前后的估计系数都为正,分别为0.784和0.902,且高度显著,说明房产税改革前后,上一期房价波动增加1%,本期房价波动会相应的增加0.784%和0.902%。再来看房产税税率的估计结果,从(3)列dGMM估计结果来看改革前后房产税税率的估计系数均为负,分别为-0.027和-0.035,且高度显著;而(4)列sGMMM估计结果来看,改革前房产税税率的系数为正但不显著,改革后房产税税率的系数在5%水平上显著为负,是-0.060。通过以上房产税试点改革前后的结果与全时段结果进行对比分析发现,房价波动的滞后一期与房产税税率对房价波动的影响均有所增加,说明房产税改革后房产税对房价波动的抑制作用更明显。这同时也说明,随着中国房地产市场的发展,房价波动自身的调节、房产税对房价的抑制以及经济发展水平对房价的影响都在发生变化。下面,本文将进一步从不同的区域展开房产税对房价波动的影响分析。
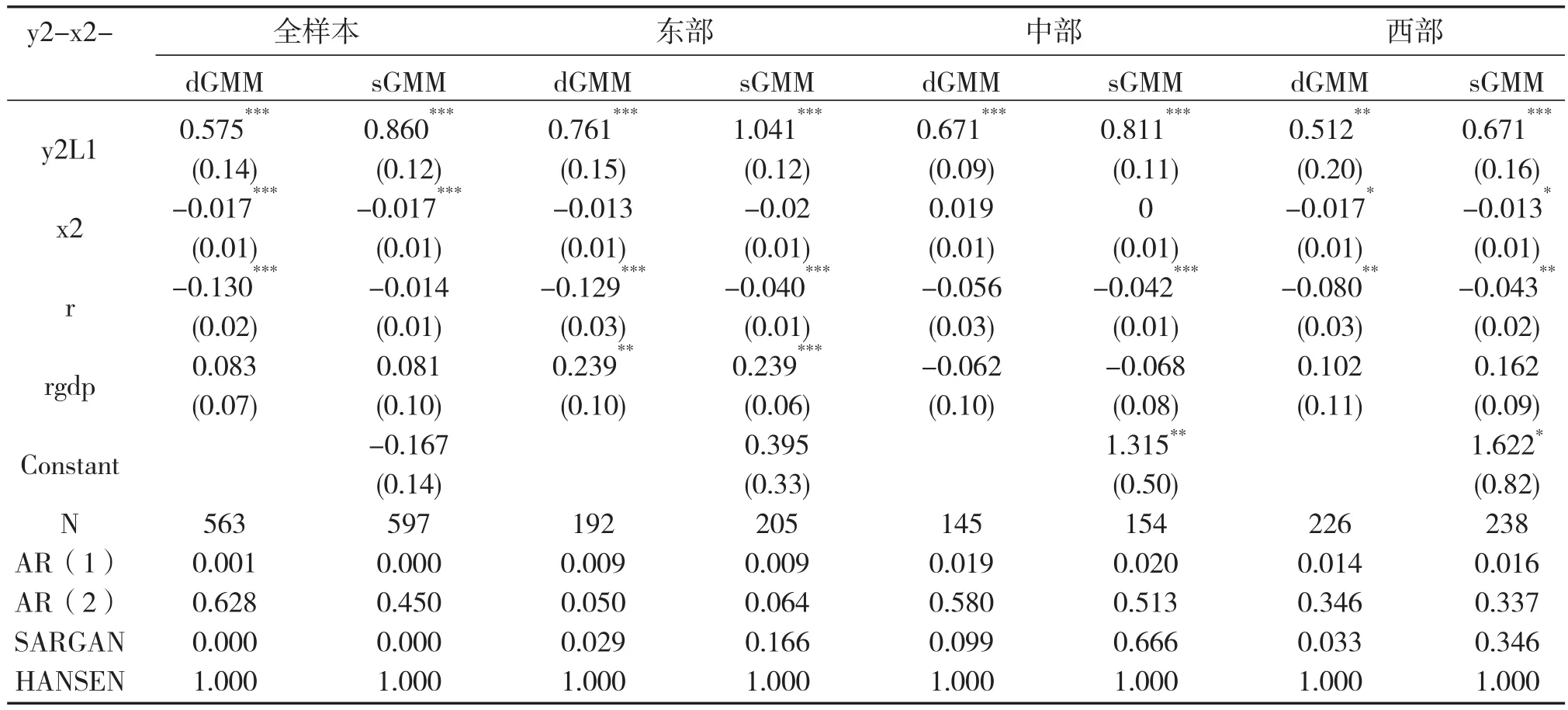
表4 全样本与分地区回归结果汇总表
具体来看,三大区域房价波动的滞后一期系数均为正,且都高度显著,系数最大的东部地区,分别是0.761和1.041,系数最小的是西部地区,分别是0.512和0.671,这说明东部地区房价波动的自我正向反馈效应最强,西部最弱。从房产税的估计系数来看,东部和中部地区都不显著,只有西部地区在10%的水平上显著为负。因此,以上分析进一步肯定了房产税对房价波动的抑制作用,同时对不同地区的回归结果也肯定了西部地区房产税对房价波动的抑制作用更为显著。这也说明,房产税对房价波动的抑制作用存在地区效应。
(三)稳健性检验
为了保证回归结果的稳健性,本文从以下两个途径对上述回归结果进行稳健性检验:一是采用更加适用于小样本且截面和时间相差不大的面板数据模型的BCFE估计方法对上述结果进行重新估计;二是更换被解释变量的衡量指标,采用y、y1、y2作为衡量房价波动的被解释变量分别对全时段、分时段和分区域进行回归。相比较于差分GMM,系统GMM能够更好地解决弱工具变量问题。但是,当面对小样本数据结构时,BCFE估计不会受到条件异方差的影响,回归结果要优于dGMM和sGMM。
四、结论和启示
通过上文分析和稳健性检验,得出以下结论:一是房产税具有抑制房价波动的作用。理论分析表明,房产税税率越高房价波动越小,实证分析也支持了理论分析的结论。通过分区域的实证分析发现,三大区域中西部地区房产税的抑制作用最为显著。二是房产税对房价波动的抑制作用随着房产税改革的推进会变得更加有效。
对我国未来房产税改革的几点启示:一是将房产税改革与房地产市场结构优化相结合。推进租购同权改革,优化租房市场与购房市场之间的关系。二是将居民用房与商业用房的房产税进行组合改革。坚持因地制宜的灵活改革模式,避免“一刀切”的改革模式。三是将房产税改革与宽松的利率政策相结合。短期内房产税改革对宏观经济的负面影响得到对冲,同时房产税改革对房价的长期调控作用得到保留。

