重庆曾家岩大桥多杆件特殊节点模型试验设计

魏思斯， 耿 波， 尚军年， 郑 植,3

(1.招商局重庆交通科研设计院有限公司， 重庆 400067； 2.桥梁工程结构动力学国家重点实验室， 重庆 400067；3.重庆大学 土木工程学院， 重庆 400045)

近年来，随着我国高速铁路、城市轨道交通的快速发展，为了高效利用过江通道，修建了许多公铁、公轨两用桥梁[1-2]。在经典连续钢桁梁的基础上，组合刚性悬索加劲弦形成的悬索加劲钢桁梁桥，俨然已成为一种适用于公铁、公轨两用桥梁的新式结构。悬索加劲钢桁梁桥造型美观，但结构构造复杂，受力行为不明确，其刚性悬索与上弦杆的连接处涉及众多杆件，受力及构造特点比起常规的整体节点更为复杂，本文对这一类连接简称为特殊节点[3]。

目前，该类型桥梁中，国内建成了东莞市东江双层公路特大桥[4]、石济客专济南黄河公铁两用大桥[5-6]、钱塘江公轨两用大桥[7]。2009年建成的东莞市东江大桥在设计时针对特殊节点开展了试验研究。彭振华[4]和谭明鹤等[8-9]开展了缩尺比例为1∶2的模型试验，在加劲弦、左侧斜腹杆和右侧竖腹杆端部设置铰约束，在上弦杆两端、左侧竖腹杆和右侧斜腹杆端部分别采用千斤顶同步施加轴向荷载，试验加载至设计荷载的70%，试验结果验证了东江大桥特殊节点的安全性。

主跨208 m的东江大桥和主跨180 m的石济客专济南黄河公铁两用大桥[10]，主梁均采用3片主桁承载，其中东江大桥采用板桁分离桥面系，主桁受力较为明确，且加劲弦与上弦杆通过在一个主节点共用变高度的竖版即合并为一根杆件，特殊节点的规模较小；主跨270 m的曾家岩嘉陵江大桥是城市公轨两用桥梁中的首座悬索加劲钢桁梁桥，主桁仅采用空间2片桁架结构[3]，上桥面采用纵横梁体系的正交异性板整体桥面，桥面板、横梁与主桁共同承载将引起次内力[4]，受力较为复杂，且加劲弦与上弦杆经过一个节间的距离才逐渐合并为一根杆件，过渡范围较大。

综上分析，由于曾家岩大桥特殊节点涉及的加劲弦、上弦杆、腹杆等众多杆件，涵盖上弦杆中2个节点，规模较大，且采用正交异性板整体桥面，特殊节点受力因桥面系的影响，其受力及构造特点比起常规的整体节点更为复杂，其模型试验边界荷载的模拟也无法直接借鉴东江大桥节点试验的经验。因此，需通过模型试验对曾家岩嘉陵江大桥特殊节点的静力性能进行研究，而试验设计的合理性是保障模型试验顺利进行的关键。由于受试验条件的限制，难以实现空间三维加载，如何将多杆件节点三维受力状态转化为平面内受力，合理处理模型几何边界条件，保证荷载的顺利施加与传递，准确模拟特殊节点关键部位的应力状态是本试验设计的难点。为此，本文对多杆件节点模型边界的模拟与实现、荷载施加方式的确定、反力台座及缩尺试验件的设计展开研究，以期为后续类似多杆件节点的试验研究与设计提供参考。

1 工程概况

重庆曾家岩嘉陵江大桥为悬索加劲连续钢桁梁桥，跨径布置为(135+270+135)m[11]，桥型布置见图1。主桁采用横向中心距为26.7 m的空间2片桁架结构，钢桁梁中心桁高12.483 m[3，11-13]。上层桥面为采用纵横梁布置的梁格体系的正交异性桥面板，板厚16 mm[11]。

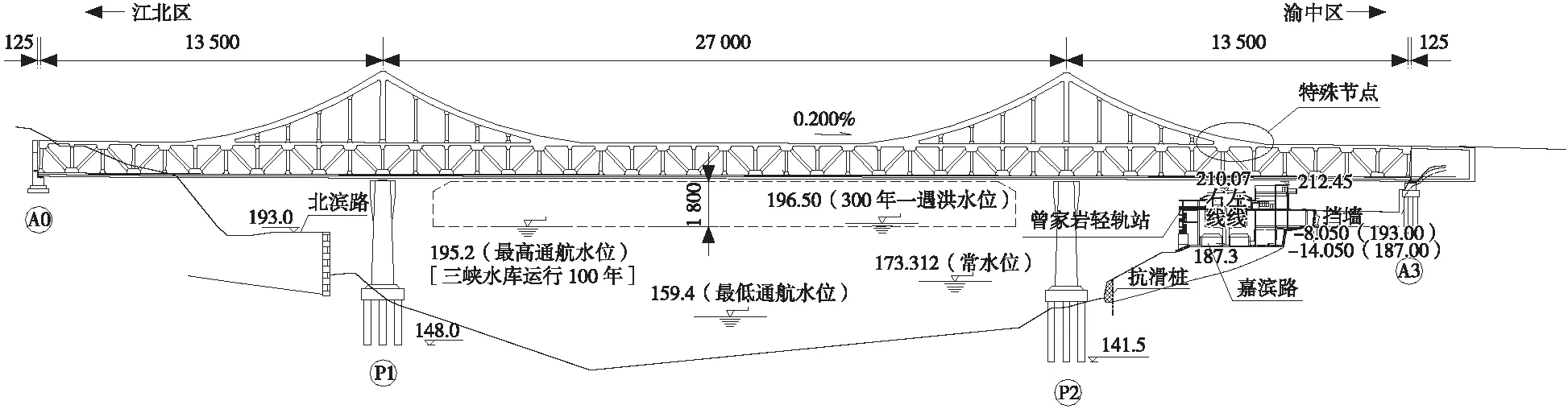
单位：cm图1 曾家岩嘉陵江大桥总体布置Fig.1 General layout of Zengjiayan Jialing River Bridge

根据全桥分析结果[14]可知，渝中区侧边跨特殊节点内力最大，故选该部位为本文研究对象。在该侧边跨内，S37S38加劲弦与A37A38上弦杆交汇于A38节点，并合成一根变高度的A38A39上弦杆[3]。加劲弦与上弦杆的连接始于A38节点，并经过整个节间，结束于A39节点，见图2。

图2 特殊节点构造Fig.2 Configuration of special joint

2 试验模型几何与荷载边界的确定

由于受到试验条件的限制，难以实现空间三维加载，本试验仅选取特殊节点在主桁平面内的杆件，并简化为平面内加载。先根据全桥多尺度有限元模型[15]分析结果对特殊节点边界荷载进行分析，并结合节段模型试算结果，确定试验模型的几何与荷载边界，使得节段模型能较为准确地模拟特殊节点关键部位的应力分布规律。由此确定的边界模拟形式为：S38S37加劲弦杆端固结，A39B39竖腹杆端部设置固定铰支座，并在其余杆端均施加轴向荷载，见图3。为了使特殊节点节段模型在面内受力平衡，并尽量准确模拟S37S38的加劲弦和A38节点板的应力分布情况，将桥面板承担的水平向力附加在上弦杆上，而上层桥面系横梁承担的竖向力则附加在竖腹杆上。该边界模拟形式对应节段模型的应力分布见图4。

图3 缩尺模型加载示意Fig.3 Loading diagram of scaled model

单位：MPa图4 特殊节点节段模型Von-Mises应力分布Fig.4 Von-Mises stress distribution of Special-joint segmental model

将图4中特殊节点节段模型各主要受力构件的应力分布情况与全桥模型分析结果进行对比：1) 特殊节点加劲弦的Von-Mises应力分布规律与全桥多尺度模型分析结果接近，相同部位存在应力集中，最大Von Mises应力为359.4 MPa，总体应力水平在196.1 MPa以内，特殊节点的Von-Mises应力水平接近实际情况；2) 采用该边界形式进行模拟时，特殊节点节段模型中上弦杆和A39B39竖腹杆的应力水平高于全桥多尺度模型的计算结果，这是由于由桥面系传递的部分荷载分别附加在了上弦杆和A39B39竖腹杆中；3) 节段模型能较为准确地模拟特殊节点关键部位的应力分布规律，因此，该边界形式可作为特殊节点缩尺模型设计的依据。

3 反力台座设计

3.1 特殊节点加载方案

综合考虑现有加载能力及试验场地、测试内容、钢材种类、模型加工等因素，对试验缩尺模型的缩尺方案进行比选，最终确定试验模型的缩尺比例为1∶2.5。据相似理论，按照1∶2.5缩尺后得出的各杆端在1.0倍设计荷载工况和超载工况[16](1.4倍设计工况，对应图3中括号内数值)下需施加的荷载值见图3。

当加载至100%设计荷载时，需施加的最大荷载为282.7 t；1.4倍超载时，需施加的最大荷载为395.8 t，可采用400 t千斤顶进行加载。A38节点竖腹杆1.4倍超载时需施加的最大荷载为45.6 t，采用300 t千斤顶进行加载。试验加载设备利用高稳定性液压加载控制器和5个高精度液压千斤顶进行，荷载大小采用振弦式锚索测力计测量，使用之前须标定。

3.2 反力台座设计

施加的最大荷载达到395.8 t，且为了模拟固结的边界条件，需将加劲弦的一段预埋在钢筋混凝土的反力墙中，该固结部位受到轴向拉力11 701.0 kN、剪力221.4 kN及弯矩575.2 kN·m的作用，加载吨位和加劲弦端部反力较大，并需在5处同时加载，为保证试验的实施，设计了强大的混凝土反力墙及底座。试验台座的基本构造及节点加载方案见图5。

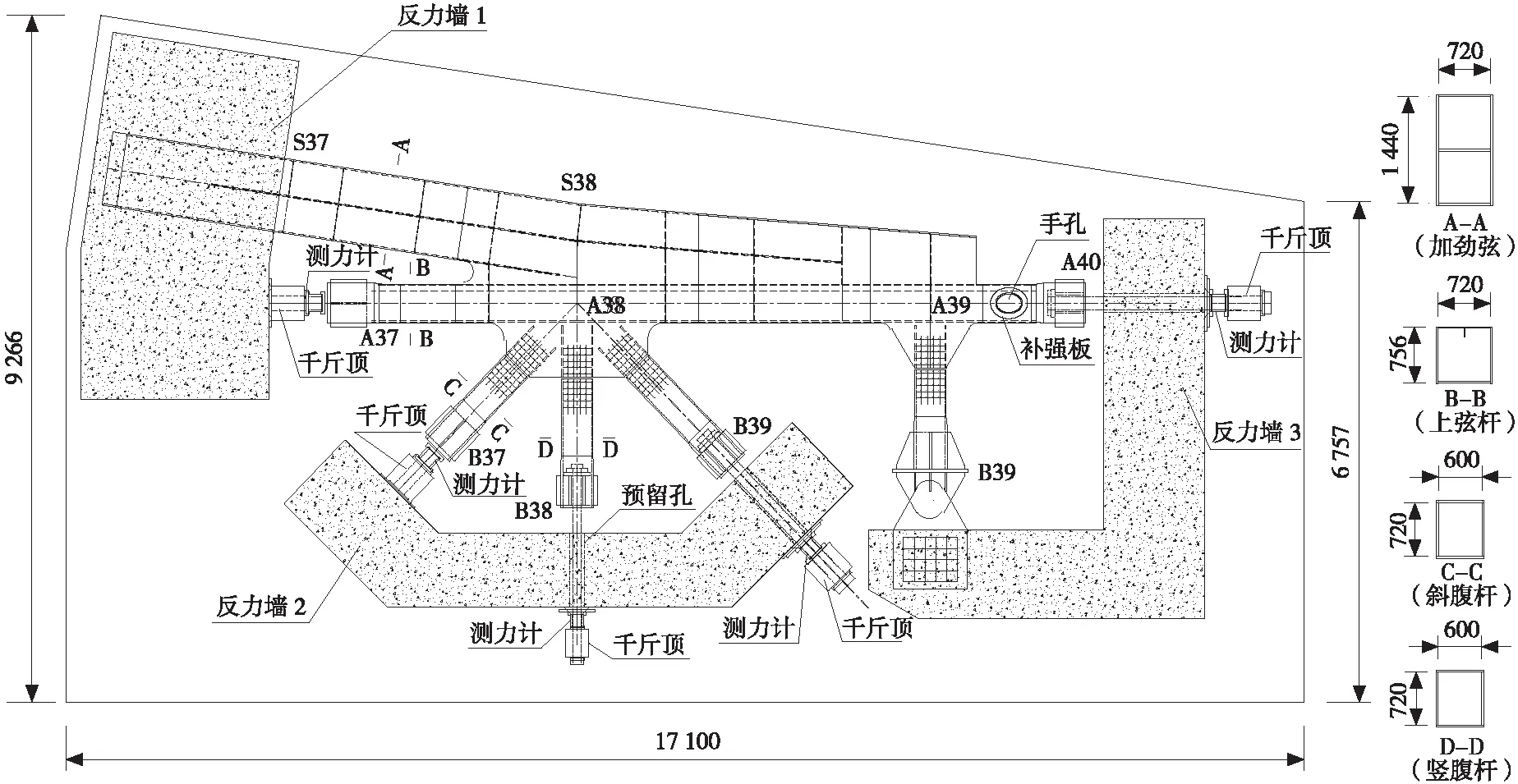
单位：mm图5 特殊节点加载方案平面Fig.5 Plan view of loading of special joint

由图5可知，试验台座由1 m厚的底座和3道高1.5 m的反力墙组成。试件平躺安装在试验台座上，加劲弦嵌入反力墙1中固结，A39节点竖腹杆端部设置铰支座，主耳板嵌入反力墙3中固定，其余杆件端部均采用千斤顶施加轴向荷载。为了在A38节点竖腹杆和右侧斜腹杆以及A39节点侧上弦杆杆端施加轴向拉力，将预应力钢束一端锚固在缩尺模型杆件内，穿过反力墙中的预留孔在另一端通过千斤顶张拉。千斤顶与反力墙接触处均设置预埋钢板，以扩大反力墙受力面积，防止混凝土局部被压溃。

锚固加劲弦的反力墙1厚2.6 m，反力墙2厚1.2 m，L形反力墙3在固定铰支座处厚1.2 m、在对上弦杆施加轴向拉力处厚1.4 m。底座和反力墙均采用C50混凝土，反力墙的纵向受力钢筋和箍筋均采用HRB400，纵向受力钢筋采用单肢Φ28，间距120 mm，抗剪钢筋采用Φ16的钩筋。通过计算分析，反力墙正截面抗弯和斜截面抗剪均满足要求，且有较高的安全储备。

考虑到通过千斤顶来施加荷载，反力墙加载处设置了方格网作为间接钢筋来抵抗局部受压，根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362—2018)[17]5.7.2条，经验算其局部受压区的截面尺寸满足要求。

4 特殊节点缩尺模型设计

本试验特殊节点涉及加劲弦、上弦杆、斜腹杆、竖腹杆共计7根杆件，需在S38S37加劲弦杆端固结，在A39B39竖腹杆杆端设置铰接，并在其余5根杆件端部施加轴向压力或者拉力，如何实现边界的模拟，并保障荷载的顺利施加与传递是本试验试验模型设计的难点，也是确保试验成功实施的关键。本节对多杆件节点试验模型的细部构造进行设计。

4.1 缩尺模型各组件及连接设计

在试验段模型的几何尺寸严格按照1∶2.5的比例缩尺，A38节点板按照比例缩小后厚度为22.5 mm，无该板厚规格的钢板，故将其板厚微调到了24 mm。同时综合考虑反力台座的设计及加载设备所需的空间，对部分杆件的长度进行了调整。特殊节点1∶2.5缩尺模型整体构造和各杆件的截面见图5。

加劲弦的翼板、顶板、底板、横隔板板厚均为20 mm。上弦杆顶板板厚8 mm，底板和竖板板厚16 mm，顶板加劲弦肋厚6 mm。斜腹杆和竖腹杆翼板板厚分别为20 mm和16 mm。A38、A39节点板板厚分别为24 mm和20 mm。

试验件全长13.587 m，宽5.055 m。加劲弦嵌固在反力墙内，并在嵌入范围内的外表面均匀布置剪力钉，以保证其与反力墙的有效固结。固定铰支座耳板嵌固于反力墙内，与A39B39竖腹杆杆端布置的2块耳板经由销轴连接以实现铰接。

试验中拉力施加方式的设计，对试验的顺利开展十分重要。通过查阅文献及借鉴有关工程经验[18]，采用在构件端部穿入钢束，并通过千斤顶张拉可靠锚固的钢束，来实现荷载的施加。即将预应力钢束锚固在A39A40上弦杆、A38B39斜腹杆以及A38B38竖腹杆内，钢束穿过反力墙的预留孔在另一侧由穿心式千斤顶牵引施加拉力[1]。为了便于预应力钢束及固定端锚具的安装，上弦杆A38A40开有椭圆形手孔，并加焊宽70 mm厚30 mm的补强板。A38A37上弦杆、A38B37斜腹杆杆端则由千斤顶直接施加压力。

考虑试验件制作加工、运输及安装的的可行性，A38节点与加劲弦、上弦杆以及A39节点与上弦杆由栓接改为焊接，采用融透的对接焊缝，腹杆与A38、A39节点的连接仍为高强螺栓连接。试验件坡口尺寸和焊脚高度与实桥相似。

本静力试验件A38、A39节点与腹杆之间的连接采用M24高强螺栓，根据《铁路桥梁钢结构设计规范》(TB 10002.2—2017)[19]按照连接杆件的强度进行螺栓数量的设计计算，即螺栓连接的强度不应低于被连接杆件的强度。

4.2 缩尺模型杆端局部加强部位设计

1) 构造设计

为了保证荷载安全可靠地传递，各杆端施加荷载部位需进行局部加强。其中，A39A40上弦杆、A38B39斜腹杆以及A38B38竖腹杆杆端施加轴向拉力处，由于需要预留预应力钢束通过的空间，采用井字形加劲；其余杆件端部施加轴向压力，则采用十字加劲。杆端局部加强部位的翼板、端板及加劲板板厚增大为30 mm[3]。局部加强部位构造见图6、图7。

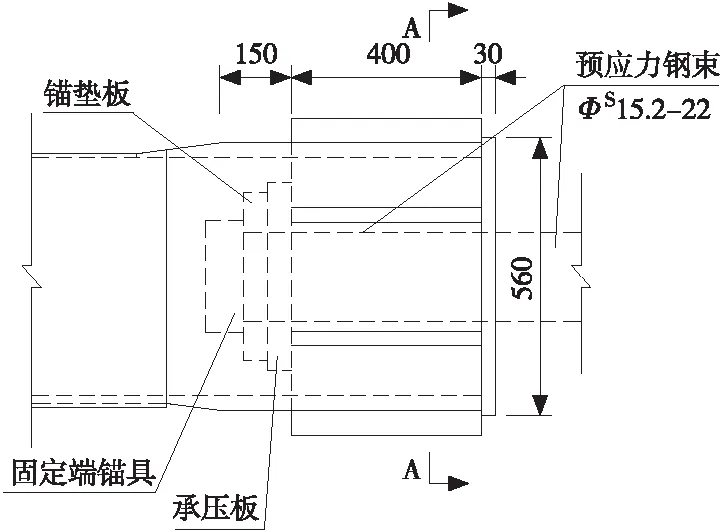
(a) 平面

(b) A-A断面单位：mm图6 井字形加强构造Fig.6 Configuration of well-shape reinforcement

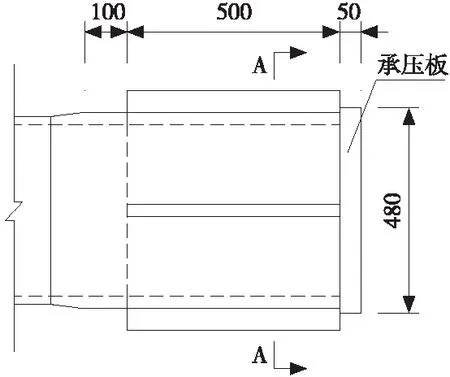
(a) 平面

(b) A-A断面单位：mm图7 十字形加强构造Fig.7 Configuration of cross-shape reinforcement

各杆件按1∶2.5缩尺后，杆件内边缘尺寸低于500 mm，操作空间较小，在杆件内部施焊难以操作。为了便于操作，杆件局部加强区域内，杆件翼板在加劲板的位置开槽，加劲板先焊接成为整体(十字形或者井字形)，然后插入杆件翼缘槽口，并在翼缘外侧进行焊接。

2) 设计验证

局部加强部位的安全性和可靠性通过局部有限元分析得到验证。A39A40上弦杆在超载工况需要施加的轴向拉力最大，为395.8 t，且该处翼板开有手孔，截面被削弱，故取该部位进行井字形加强部位的局部分析，取端板到端部手孔以下1倍边长范围内的杆件为研究对象，利用Midas FEA建立三维板壳单元模型，压力荷载通过面压力进行模拟，杆件底部固结，见图8。加劲板伸出杆件翼板是为了方便施焊，不影响力的传递，因此本模型中仅建出杆件内部的加劲板。

(a) 杆件翼板

(b) 加劲板、端板、承压板图8 井字形加强部位局部有限元模型Fig.8 Local finite element model of the well-shape reinforcement

千斤顶施加的压力通过应力钢束及固定端锚具传递到承压板，再传到井字形加劲板，然后通过焊缝传给杆件翼板，计算结果见图9。从图9可以看出，加劲板与杆件翼板焊缝在承压板位置处Von-Mises应力最大，为143.4 MPa。杆件翼板开孔处在短轴顶点附近存在应力集中，最大Von-Mises应力达到了334.7 MPa，但应力集中范围较小，且最大Von-Mises应力小于钢材的屈服应力，认为翼板受力是安全的，能够有效传递荷载。加劲板在与承压板接触位置Von-Mises应力最大，为276.2 MPa，尽管大于钢板的容许应力(247 MPa)，但仍小于屈服强度，仍然是安全的。该位置不是重点关注范围，仅需要保证荷载的安全传递，因此认为井字形加强部位的设计是合理的。

(a) 杆件翼板

(b) 加劲板单位：MPa图9 井字形加强部位Von-Mises应力分布Fig.9 Von-Mises stress distribution of the well-shape reinforcement

A38A37上弦杆在超载工况需要施加的轴向压力最大，为346.0 t，故取该部位进行局部分析，取端部3倍边长范围内的杆件为研究对象，利用Midas FEA建立三维板壳单元模型，压力荷载通过面压力进行模拟，杆件底部固结。十字形加强部位有限元模型见图10，本模型也仅建出杆件内部的加劲板。

(a) 杆件翼板

(b) 加劲板、端板图10 十字形加强部位局部有限元模型Fig.10 Local finite element model of the cross-shape reinforcement

千斤顶施加的压力通过端板传到十字形加劲板，再通过焊缝传给杆件翼板，计算结果见图11。从图11可以看出，加劲板与杆件翼板焊缝在承压板位置处Von-Mises应力最大，为122.4 MPa；承压板最大Von-Mises应力为184.7 MPa；加劲板在与端板接触位置Von-Mises应力最大，为185.4 MPa，低于钢板的容许应力247 MPa，表明十字形加强部位的设计是合理的。

(a) 杆件翼板

(b) 加劲板单位：MPa图11 十字形加强部位Von-Mises应力云图Fig.11 Von-Mises stress distribution of the cross-shape reinforcement

4.3 缩尺模型加劲弦嵌固端设计

1) 构造设计

为了在S38S37加劲弦杆端施加固定约束，加劲弦在试验区域范围外延伸2.4 m嵌入反力墙1内，并在加劲弦四面翼板外侧布置剪力钉，以保证加劲弦与反力墙的有效连接。为了使混凝土能够进入加劲弦内部并尽量密实，在加劲弦灌浆侧顶板开孔，且顶板在端部缩短200 mm，见图12。

单位：mm图12 加劲弦固结端构造Fig.12 Configuration of the embedded end of stiffening chord

2) 设计验证

根据计算求得的嵌固端的反力，并考虑1.4倍超载可知，S38S37加劲弦杆端受到轴向拉力11 701.0 kN、剪力221.4 kN及弯矩575.2 kN·m的作用。为了保证加劲弦嵌固端与反力墙1有效连接，根据《公路钢混组合桥梁设计与施工规范》(JTG/T D64-01—2015)[20]对剪力钉连接件的承载能力极限状态和正常使用极限状态进行设计计算。

本静载试验选用d=22 mm的圆柱头焊钉为剪力连接件，材料为ML15。在锚入反力墙的加劲弦4个外表面上共布置260个剪力钉，单个剪力钉受到的剪力为45.0 kN，单个剪力的抗剪承载力为85.14 kN，安全系数为1.90，强度满足规范要求。剪力钉结合面的最大滑移为0.148 mm，小于规范中的限值0.2 mm，表明结合面滑移也满足规范要求。

4.4 缩尺模型铰支座设计

1) 构造设计

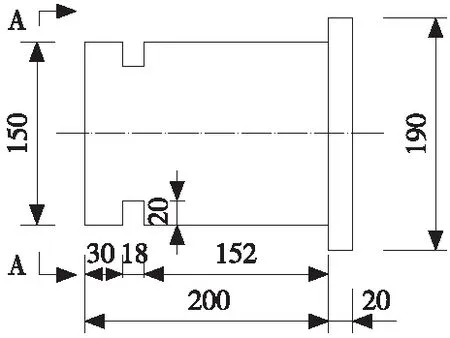
根据《钢结构设计标准》(GB 50017—2017)[21]11.6节的规定拟定了铰支座的结构尺寸，铰支座耳板、销轴构造分别见图13和图14。主耳板板厚60 mm，次耳板板厚40 mm，销轴直径150 mm。铰支座耳板采用Q420qE钢材，销轴采用40 Cr。

(a) 次耳板

(b) 主耳板单位：mm图13 铰支座耳板构造Fig.13 Configuration of the hinged support

(a) 销轴立面

(b) A-A断面单位：mm图14 销轴构造Fig.14 Configuration of the axis pin

2) 设计验证

根据计算求得的铰支座的反力，1.4倍超载加载时，B39A39竖腹杆铰支座的轴向反力为1 617.7 kN(受拉)，剪力为139.1 kN。作用在铰支座上的合力为1 623.7 kN。

铰支座耳板的安全性和可靠性通过局部有限元分析进行了验证，有限元模型见图15。反力墙3、台座及主耳板均采用三维实体单元进行模拟，预埋耳板一部分嵌入反力墙3中，将作用在铰支座的荷载以集中力的形式进行施加，主耳板最大Von-Mises应力为151.8 MPa，小于Q420qE钢材的容许应力241 MPa，表明主耳板强度满足要求。

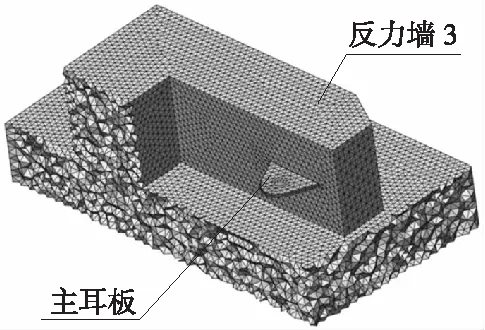
(a) 有限元分析模型

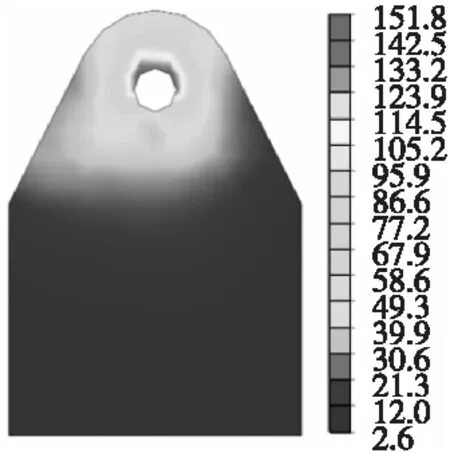
(b) Von-Mises应力云图单位：MPa图15 主耳板有限元分析验证Fig.15 Verification of the main ear plate by finite element analysis

为了保证铰支座主耳板与反力墙3有效连接，根据《公路钢混组合桥梁设计与施工规范》(JTG/T D64-01—2015)[20]对耳板剪力钉连接件的承载能力极限状态和正常使用极限状态进行设计计算。在嵌入反力墙的主耳板顶底面上共布置60个剪力钉，选用d=22 mm的圆柱头焊钉为剪力连接件，材料为ML15。单个剪力钉受到的剪力为27.1 kN，单个剪力的抗剪承载力为85.14 kN，安全系数为3.15，强度满足规范要求。剪力钉结合面的最大滑移为0.091 mm，小于规范中的限值0.2 mm，表明结合面滑移也满足规范要求。

5 结论

本文基于特殊节点的边界荷载分析，确定了试验模型的边界模拟形式，并制定了试验加载方案，在此基础上设计了多杆件特殊节点缩尺试验模型及反力台座，得到以下结论：

1) 加劲弦S38S37杆端固结，竖腹杆A39B39端部设置铰支座，并在其余杆端采用施加轴向荷载的方式来模拟特殊节点的边界荷载，将空间受力简化为面内受力，节段模型能较为准确地模拟特殊节点关键部位(加劲弦、加劲弦与上弦杆交界处以及A38节点板)的应力分布规律。

2) 根据缩尺试验件施加的荷载及反力，设计了由1 m厚的底座和3道高1.5 m的反力墙组成的反力台座，试件平躺安装在试验台座上，加劲弦嵌入反力墙1中固结，A39节点竖腹杆端部设置铰支座，主耳板嵌入反力墙3中固定，其余杆件端部均采用千斤顶施加轴向荷载，由此实现多杆件特殊点几何与荷载边界的模拟。

3) 根据缩尺比例确定试验模型各组件的尺寸，根据相关规范对杆件间的连接、加劲弦嵌固端及铰支座进行设计计算，并通过局部有限元分析验证了杆端十字形及井字形加强部位、铰支座的安全性，最终确定了特殊节点缩尺模型的结构构造。

4) 本模型试验目前已完成，最大加载至设计荷载的1.4倍，测试模型各杆件端部位移以及关键部位的应力分布，结果显示，缩尺模型在受荷载过程中处于弹性工作阶段，试件受力均衡，各剖面测点处实测应力分布规律与理论计算结果基本吻合，在1.4倍设计荷载(超载工况)作用下，所有测点应力仍然小于钢材的容许应力，结构的静力安全储备足够。试验台座及缩尺模型各连接部位、局部加强部位、加劲弦嵌固端以及铰支座均正常工作，能够安全可靠地传递试验荷载，试验设计安全可靠。