基于缠绕式FBG传感器的斜拉索镀锌高强钢丝腐蚀定量监测方法研究

严 琨， 刘国栋， 张 恒， 吴伟豪， 龙 彬， 李 琦

(1.招商局重庆交通科研设计院有限公司， 重庆 400067； 2.重庆交通大学， 重庆 400074； 3.重庆万桥交通科技发展有限公司， 重庆 401336； 4.中交公路长大桥建设国家工程研究中心有限公司， 北京 100088)

斜拉索作为斜拉桥的“生命线”，既能将主梁恒载和活载传递至桥塔，又能约束桥塔的变形，起到承上启下的作用。斜拉桥在施工和运营期间，因斜拉索防护失效，致使钢丝接触到水分而出现腐蚀现象，如果不能对拉索内高强钢丝的腐蚀情况进行监测和准确的评估，一旦发生安全事故，将造成极大的不良社会影响和巨大的经济损失。

传统检测方法[1-3]如磁漏检测法、超声检测法、放射线检测法、人工目检法，因耐久性差、测量精度低、稳定性不高等原因，难以满足对拉索内部钢丝腐蚀状况进行定量检测的要求[4]，若更换后对拉索采用解剖检测的方式，可精确检测拉索与钢丝的力学性能和腐蚀状态，但周期长、成本高。

光纤光栅作为新兴的传感技术，监测钢构件的腐蚀，具有传感器体积小、精度高等特点[5]。根据钢构件腐蚀后膨胀的特点，研究者们设计了不同结构类型的FBG传感器[6-9]，主要有：Fe-C膜式FBG传感器、双筋式FBG腐蚀传感器、夹持式FBG腐蚀传感器、弹簧机构式FBG传感器。但斜拉索内部空间小，无法放置体积过大的传感器，上述FBG腐蚀传感器主要用于钢筋的腐蚀监测，均无法用于斜拉索内部高强钢丝的腐蚀监测，另外钢筋与高强钢丝的应用环境及组成成分有所差别，因此，无法将用于监测钢筋的FBG腐蚀传感器直接用于高强钢丝监测。

为此，专门设计一种缠绕式FBG传感器，将FBG传感器以一定的螺距缠绕在直径为7 mm的镀锌钢丝表面，并通过水浴试验测试其温度灵敏度系数、通过加速盐雾试验获得FBG传感器波长变化率与钢丝腐蚀率之间的定量关系。

1 缠绕式FBG传感器设计

1.1 缠绕式FBG传感器结构

缠绕式FBG传感器主要由镀锌高强钢丝、裸FBG传感器及外护套组成，如图1所示。传感器钢丝为斜拉索用直径为7 mm的镀锌高强钢丝。缠绕式FBG传感器的制作首先将钢丝表面的油污洗净，然后将裸FBG传感器按照一定的螺距在钢丝上进行缠绕，同时对FBG传感器施加一定拉力(不宜超过1 000 με[10])，并采用环氧胶对光纤两端进行固定，最后将尾纤用护套管进行保护，及在光纤缠绕部分用外壳进行保护。

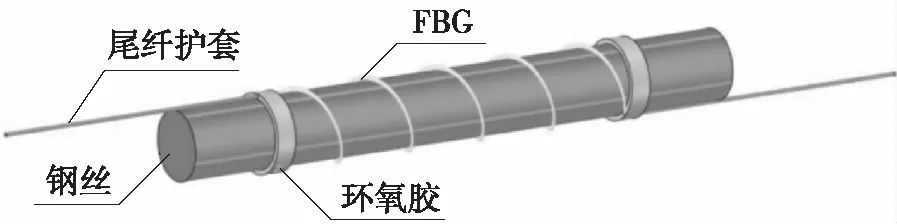
图1 FBG腐蚀传感器示意(未示出保护外壳)Fig.1 Diagram of FBG corrosion sensor(without showing protective case)

缠绕式FBG传感器直径小，约10 mm，能够将其置于斜拉索连接筒内，使得腐蚀传感器与斜拉索钢丝处于同一环境条件下，当斜拉索钢丝发生腐蚀时，缠绕式FBG传感器的钢丝亦同步发生腐蚀，进而通过FBG传感器的波长变化获得斜拉索钢丝的腐蚀状态并进行长期监测。

1.2 缠绕式FBG腐蚀传感器原理

假设镀锌高强钢丝处于均匀腐蚀状态，当钢丝腐蚀时其体积膨胀会引起缠绕在表面的光纤长度发生变化，即引起FBG传感器的波长发生变化。钢丝原始截面、锈蚀后的截面如图2(a)所示，将一个螺距范围内的光纤光栅沿钢丝轴心展开成平面后其几何图形如图2(b)所示。

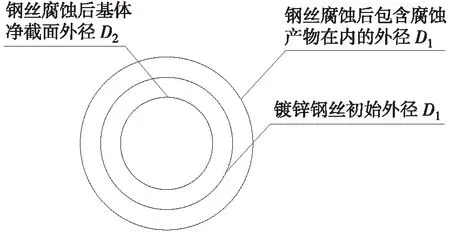
(a) 钢丝原始及锈蚀后的截面

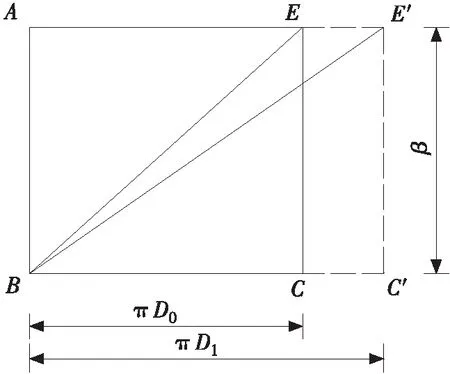
(b) 光纤螺旋线展开图图2 光纤力学分析简图Fig.2 Mechanical analysis of optical fiber

由图2(a)可见，镀锌高强钢丝腐蚀膨胀后，钢丝周长变化率为：

(1)

式中：εs为钢丝周长变化率；D0为镀锌高强钢丝初始外径；D1为钢丝腐蚀后包含腐蚀产物在内的外径。

由图2(b)可见，钢丝腐蚀膨胀引起光纤轴向应变为：

(2)

式中：εf为光纤轴向应变；BE为光纤传感器变形前长度；BE′为光纤传感器变形后长度；β为光纤缠绕螺距。

将式(2)和式(1)联立消去D1，可得到钢丝周长变化率与光纤轴向应变关系：

(3)

假设钢丝腐蚀后的体积膨胀系数为ξ，则

(4)

式中：D2为钢丝腐蚀后基体净截面外径。

设一个螺距范围内的质量腐蚀率为ρm，则

(5)

式中：ρ铁为钢丝密度。

(6)

将式(3)带入式(6)中，可得质量腐蚀率与光纤轴向应变关系式：

(7)

根据Bragg衍射条件[11]，得：

λB=2neffΛ

(8)

式中：λB为FBG传感器反射光波长；Λ为FBG传感器栅距；neff为纤芯有效折射率。

当光纤产生应变时，FBG传感器栅距和有效折射率发生变化，因此有：

ΔλB/λB=ΔΛ/Λ+Δneff/neff

(9)

式中：ΔλB为测试到的FBG传感器波长变化量；ΔΛ为栅距变化量；Δneff为有效折射率变化量。

FBG产生应变时的折射率变化为：

(10)

式中：p12、p11为弹性常数；v为FBG泊松比；pe为有效弹光系数。对于纯熔融石英的光纤光栅，其参数为[12]：p11=0.121，p12=0.27v=0.17，neff=1.456，可得有效弹光系数pe=0.216。

由ΔΛ/Λ=εf，式(9)可写作：

(11)

由式(11)可得：

(12)

式中：若取波长λB=1 550 nm，则kTε=1.21 pm/με。

将式(12)带入式(7)中，并将波长单位转化为pm，可得波长变化量与腐蚀率的关系式为：

(13)

从式(13)可以看出，FBG腐蚀传感器的钢丝直径、FBG传感器的应变灵敏度系数及光纤缠绕螺距确定后，钢丝的质量腐蚀率与波长变化量关系为二次多项式关系，与钢丝腐蚀体积膨胀系数ξ为倒数关系。在实际腐蚀情况下，钢丝腐蚀体积膨胀系数ξ会随着腐蚀不断发生变化，其取值受多种因素影响，如温湿度、氧气浓度、Cl-浓度等，对于钢筋一般取值为1.1～1.8[13]。因此，在镀锌高强钢丝体积膨胀系数ξ无法准确给定的情况下，需通过试验对缠绕式FBG传感器的腐蚀率和波长变化量关系进行实测。

2 缠绕式FBG传感器腐蚀试验

2.1 光纤缠绕螺距的确定

缠绕式FBG腐蚀传感器的螺距会影响其应变灵敏度，螺距越小其灵敏度越大，但螺距减小会导致光纤的缠绕曲率半径减小，从而引起透光率下降，致使FBG传感器不可用。为确定最小螺距值，对比了FBG传感器在初始平直状态下和将FBG传感器以不同螺距(β=20 mm～40 mm)缠绕在钢丝表面的输出反射光谱图，如图3所示。

(a) 螺距35 mm时的光谱

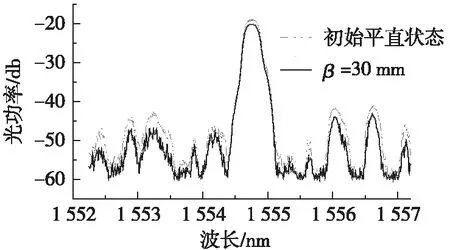
(b) 螺距30 mm时的光谱

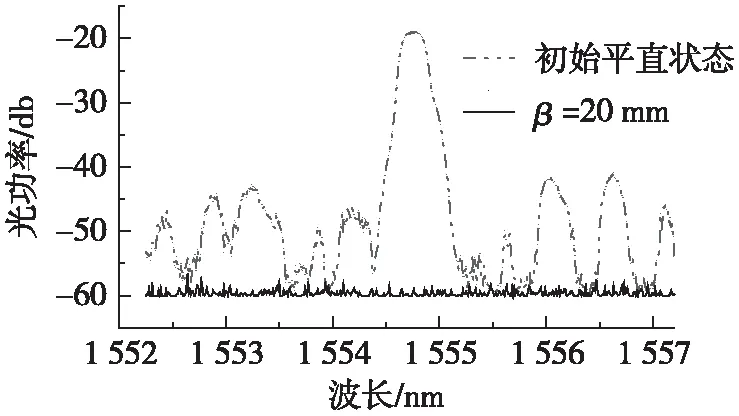
(c) 螺距20 mm时的光谱图3 不同螺距时FBG传感器反射光谱图对比Fig.3 Comparison of reflection spectra of FBG sensors with different pitches

由图3(a)可知，当螺距为35 mm时，光纤缠绕后的FBG传感器波峰与初始平直状态一致；由图3(b)可知，当螺距为30 mm时，波峰有所削弱；由图3(c)可知，当螺距小于20 mm时，波峰消失，即FBG反射信号完全丢失。因此，为避免光纤透光率下降造成FBG传感器失效，保证传感器工作性能，螺距应不小于35 mm。

2.2 温度灵敏度系数标定

由于FBG传感器对温度非常敏感[14]，因此需要对缠绕式FBG传感器的温度灵敏度系数进行标定，通常有啁啾法、温度应变双参量法、不受力FBG温度补偿法等方法[15]。综合考虑造价、可靠性、准确性等因素，采用不受力FBG温度补偿法对缠绕式FBG传感器的温度灵敏度进行标定。忽略FBG传感器的温度应变耦合效应，即假定温度与应变对FBG传感器的影响是线性的，不考虑二阶项，其波长变化为：

ΔλB 1= ΔλB0+ ΔλT1= ΔλB0+kT1ΔT

(14)

式中：ΔλB 1为FBG腐蚀传感器的波长总变化量；ΔλB0为钢丝腐蚀膨胀引起的FBG传感器的波长变化量；ΔλT1为温度引起的FBG传感器的波长变化量；kT1为温度灵敏度系数；ΔT为FBG腐蚀传感器的温度变化量。

由式(14)可得温度修正后的FBG腐蚀传感器波长变化量为：

ΔλB0= ΔλB 1-kT1ΔT

(15)

基于上式即可通过水浴试验获得FBG腐蚀传感器的温度灵敏度系数kT1。

为确定腐蚀传感器的温度灵敏度系数，分别制作5个缠绕式FBG传感器并进行水浴试验，缠绕螺距均为35 mm，如图4所示。

图4 FBG腐蚀传感器试件Fig.4 Specimen of FBG corrosion sensor

5个传感器通过水浴试验测量不同温度下的波长值见表1，FBG传感器波长与温度进行拟合后其温度灵敏度系数见表2。

表1 传感器温度响应实测值Table 1 Measured value of sensor temperature response

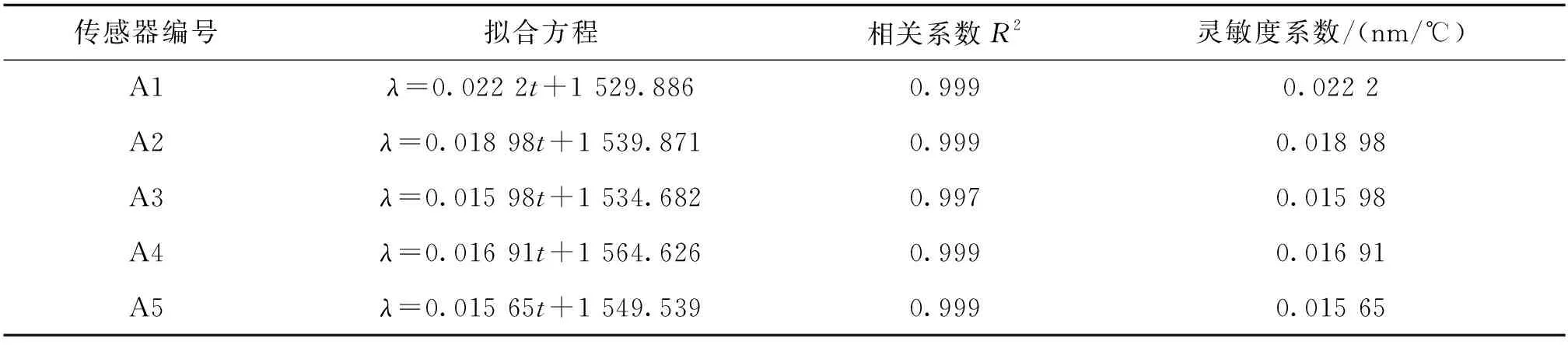
表2 传感器的波长与温度拟合方程Table 2 Fitting equation of wavelength and temperature of sensors

从表2可以看出，缠绕式FBG腐蚀传感器的波长与温度呈高度线性关系，相关系数达到0.997以上。据此，缠绕式FBG腐蚀传感器的温度影响即可采用线形修正，拟合方程中的斜率即为各个缠绕式FBG腐蚀传感器的温度灵敏度系数。

2.3 盐雾加速腐蚀试验

采用铜盐醋酸盐雾试验对前述5个缠绕式FBG传感器共进行456 h的加速腐蚀试验，试验遵循《人造气氛腐蚀试验盐雾试验》(GB/T 10125—2012)[16]的相关规定。FBG传感器的采样频率为1/60 Hz，即每分钟采集一次数据。由于传感器在试验过程中需不断采集数据，无法中途取出，因此设置对照组钢丝。对照组钢丝由35根直径为7 mm，长度为200 mm的裸钢丝组成，且与FBG腐蚀传感器钢丝均在同一根钢丝上截取，确保其直径、镀层厚度等参数一致。对照组钢丝清洗表面油污后，先称重，并作为钢丝未腐蚀的初始质量，后与FBG腐蚀传感器同时放置于盐雾试验机中，使之处于相同的盐雾试验环境，如图5所示。每隔一定时间即取出7根对照组钢丝，酸洗后，测量其腐蚀后质量，计算腐蚀率，并记录对应时刻的传感器波长值。

图5 铜盐加速盐雾试验Fig.5 Accelerated salt spray test with copper salt

考虑到镀锌层腐蚀速率较快，为得到更多镀锌层的腐蚀率，取样时间间隔前2次为48 h，后3次间隔为120 h。镀锌高强钢丝腐蚀后的质量及其腐蚀率数据见表3。

表3 高强钢丝质量腐蚀率Table 3 Quality corrosion rate of high-strength steel wire

将钢丝质量腐蚀率与时间进行拟合，如图6所示。采用Logistic函数对钢丝质量腐蚀率ρm与时间t进行拟合得到：

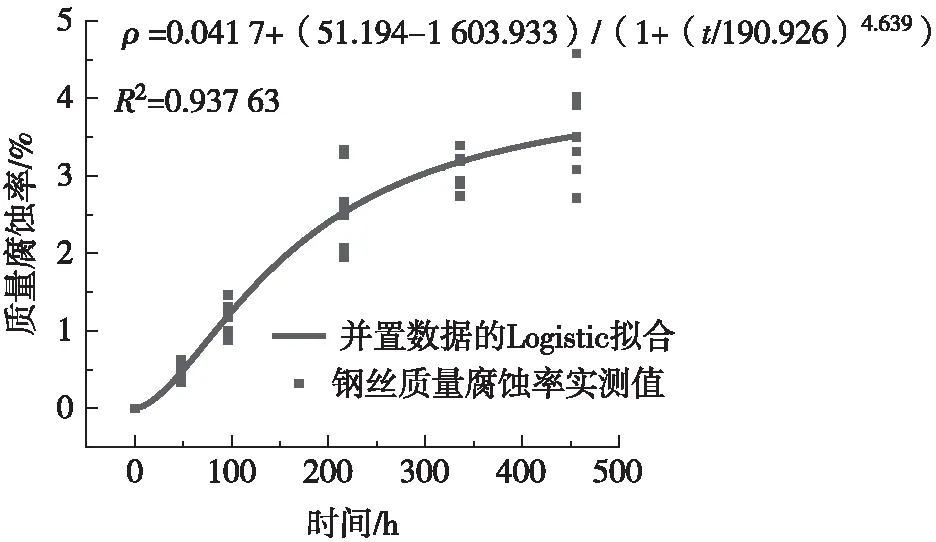
图6 腐蚀率与时间拟合曲线Fig.6 Fitted curve between corrosion rate and time

(16)

式中：t为时间，h。

从图6可以看出，钢丝腐蚀初期的腐蚀率增长速率逐渐增加，随着腐蚀率的增大，腐蚀率增长速度反而下降。原因是：腐蚀初期主要是镀锌层腐蚀，锌的活性大于铁[17-18]，因此前期腐蚀速率较快。镀锌层完全腐蚀后，铁基体开始腐蚀，同时由于腐蚀产物覆盖于镀锌高强钢丝表面，导致镀锌高强钢丝基体与腐蚀液的接触面积减小，因此腐蚀速度也随之减小。

FBG腐蚀传感器的波长变化量随时间的变化情况如图7所示。采用Slogistic1函数对FBG腐蚀传感器的波长变化量ΔλB0与时间t进行曲线拟合得：

(17)

图7 波长变化量与时间拟合曲线Fig.7 Fitted curve between wavelength variation and time

从图7可以看出，在最初约100 h内，FBG传感器的波长增长速率较小；在约100 h后，波长增长速率加快，表明此时钢丝表面镀层正处于快速腐蚀阶段；在约275 h后，波长增加速率减小，此时铁基体开始腐蚀，腐蚀速率下降，其中部分传感器的波长变化量有局部减小，这是因部分铁锈流失所导致。

FBG腐蚀传感器的波长变化量与质量腐蚀率的关系如图8所示。将波长变化量ΔλB0与质量腐蚀率ρm采用ExpAssoc函数进行拟合得到：

ρm=1.971 3×10-6+0.052 1×(1-e(-ΔλB0/2 361.336))+0.008 36×(1-e(-ΔλB0/27.426))

(18)

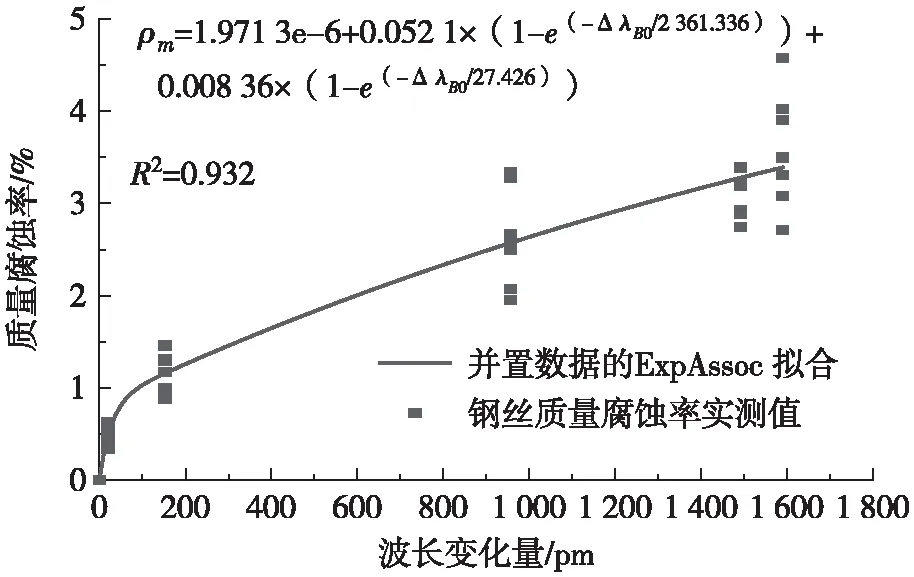
图8 波长变化量与质量腐蚀率拟合曲线Fig.8 Fitted curve between wavelength variation and mass corrosion rate

式(18)给出了质量腐蚀率与FBG腐蚀传感器波长变化量之间的关系，实际应用时将测试得到的FBG腐蚀传感器的波长变化量带入式(18)即可求得质量腐蚀率，进而判断钢丝的腐蚀程度。

2.4 镀锌高强钢丝腐蚀体积膨胀系数

镀锌高强钢丝腐蚀后的体积膨胀系数会随着腐蚀程度不断变化，根据前述实测的质量腐蚀率和波长变化量与腐蚀时间之间的关系，即将式(16)与式(17)代入到理论公式(13)中，即可得到体积膨胀系数与时间的关系，如图9所示。

图9 体积膨胀系数与时间关系Fig.9 Relationship between volume expansion coefficient and time

从图9可以看出，镀锌高强钢丝的体积膨胀系数会随着腐蚀时间而发生变化，在0～275 h时体积膨胀系数增长由慢变快，在275 h后有所降低，变化范围在1.05～1.3之间。说明随着腐蚀时间增加，腐蚀产物变得疏松，对FBG的膨胀效应减弱，而理论公式中无法考虑这一影响，因此通过式(18)更能准确反映出腐蚀率与波长变化量的关系。

3 结论

1) 通过对比光纤缠绕在钢丝表面前后的光谱，为避免光纤透光率对FBG传感器的影响，缠绕螺距值应不小于35 mm。

2) 水浴试验结果表明，缠绕式FBG传感器在常温下的温度响应线性度高，其温度灵敏度系数即为传感器的温度修正系数。

3) 盐雾腐蚀试验结果表明，传感器波长的变化趋势与高强钢丝腐蚀率变化趋势一致，能很好地反映镀锌高强钢丝的腐蚀情况。通过实测数据拟合得到钢丝腐蚀率与波长变化量的函数关系式，在实际应用时，可将实测FBG传感器的波长变化量带入该式，即可求得质量腐蚀率，从而判断钢丝腐蚀程度。

4) 锌高强钢丝的腐蚀体积膨胀系数会随腐蚀程度先增加后减小，变化范围为1.05～1.3。