车辆斜碰撞系统的非线性特性研究*

韩 宁，李万祥，李雄兵，雷菲菲

(1. 兰州交通大学 机电工程学院，甘肃 兰州 730070； 2.天水师范学院，甘肃 天水 741000)

0 引 言

对于碰撞振动系统，目前国内外学者进行了大量相关研究。Shams等[1]研究了一类单自由度振动系统，发现存在基本的周期运动和其他复杂的动力学行为。李万祥等[2]建立了一类单自由度含间隙系统，证明了hopf分岔的存在性。尹凤伟等[3]建立了一类系统模型，通过协同仿真分析了分岔机理。韩维等[4]说明了斜碰撞系统的研究现状，给出了一般的研究方法与思路。罗冠炜等[5]选取了多种力学模型，理论分析了系统周期性运动的存在条件，并研究了其分岔行为，给出了碰撞振动系统研究的基础理论与常规思路。段洁等[6]建立了三质体斜碰撞振动系统，并以碰撞间隙为变量做了减振研究。翟红梅[7]以汽轮机叶片为对象，研究了斜碰撞系统的混沌行为，分析了通向混沌的过程。

研究表明，车辆的追尾碰撞事故是高速公路上最典型的事故形态。李银龙等[8]研究了车辆的正面碰撞，建立了小角度碰撞模型并进行了模拟研究。高强等[9]研究了一类变质量动力吸振器，分析了吸振特性。笔者以车辆追尾为典型工况，抽象出五自由度斜碰撞模型，探索车辆碰撞振动系统的周期运动、通向混沌的过程和在不同减振器作用下的相对稳定性。此研究的目的在于优化车辆系统结构，对提高乘客舒适性与安全性有重要意义。

1 碰撞振动系统的力学模型

图1是由车辆追尾碰撞时简化而来的五自由度斜碰撞振动模型。后车质量为M1，前车质量为M2，两车分别由刚度为K1和K2的线性弹簧和阻尼系数为C1和C2的线性阻尼器相连，分别做铅垂方向和水平方向的运动，并且分别受到简谐激振力Pisin(ΩT+τ),(i=1,2)(碰撞激振力)的作用。后车上集成了一个质量为M3的减振器，刚度和阻尼系数分别是K5和C5。两车发生了碰撞。假设力学模型中的阻尼是Rayleigh型比例阻尼，忽略减振器M3在铅垂方向的运动，前后车在同一条直线上运动。

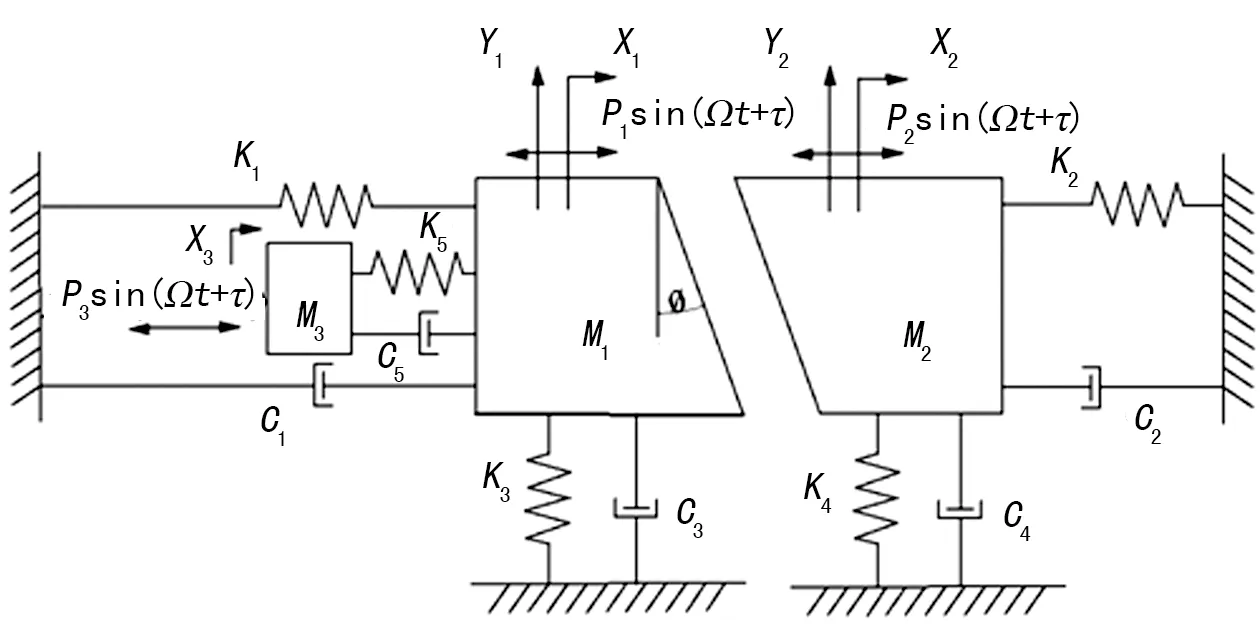
图1 车辆碰撞系统模型图

系统的运动微分方程为：

(1)

式中：Ki为线性弹簧刚度；Ci为粘性阻尼系数；Pisin(ΩT+τ)量为简谐激振力。引入无量纲量：

将上式带入得到未碰撞时的无量纲运动微分方程:

(2)

2 Poincaré映射的建立

选择庞加莱截面：

(3)

式中：φ=ωt，mod2π。

在适当的参数下，图1所示的车辆碰撞系统的动态特性表现出周期性，即设M1和M2碰撞瞬时的时间为t=0，则下一次碰撞的时间为2nπ/ω，n∈Z。用q=p/n表示系统的运动，其中p为碰撞次数，n为力周期数。

3 仿真研究与分析

(1) 倍化、逆倍化、hopf分岔、擦边现象分析

取系统参数(1)：μm1=0.2，μm2=0.5，d=0.20，ζ1=0.01，ζ2=0.01，ζ3=0.02，ζ4=0.02，ζ5=0.02，υ1=1，υ2=2，υ3=0.5，υ4=0.5，υ5=1，θ=π/12，利用Matlab编程，以外部激振频率ω为分岔参数，数值计算得到局部分叉图，如图2所示。

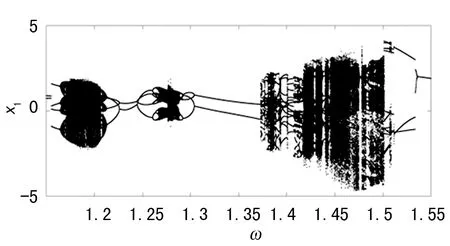
图2 局部分叉图一

数值仿真结果显示，当ω<1.153时，系统做稳定的q=2/2周期运动；当ω=1.155时，转迁至q=4/2周期运动，如图3(a)；随着ω的继续增加，原来稳定的不动点变成稳定的焦点，如图3(b)，继而变成吸引子，如图3(c)；继续增加ω至1.164 82，出现hopf圈，发生hopf分岔，如图3(d)；当ω增加到1.164 986时hopf圈不断增大、变形，失去了圆滑性，周围变得尖锐、曲折，如图3(e)；ω继续增加，系统进入了混沌，如图3(f)。

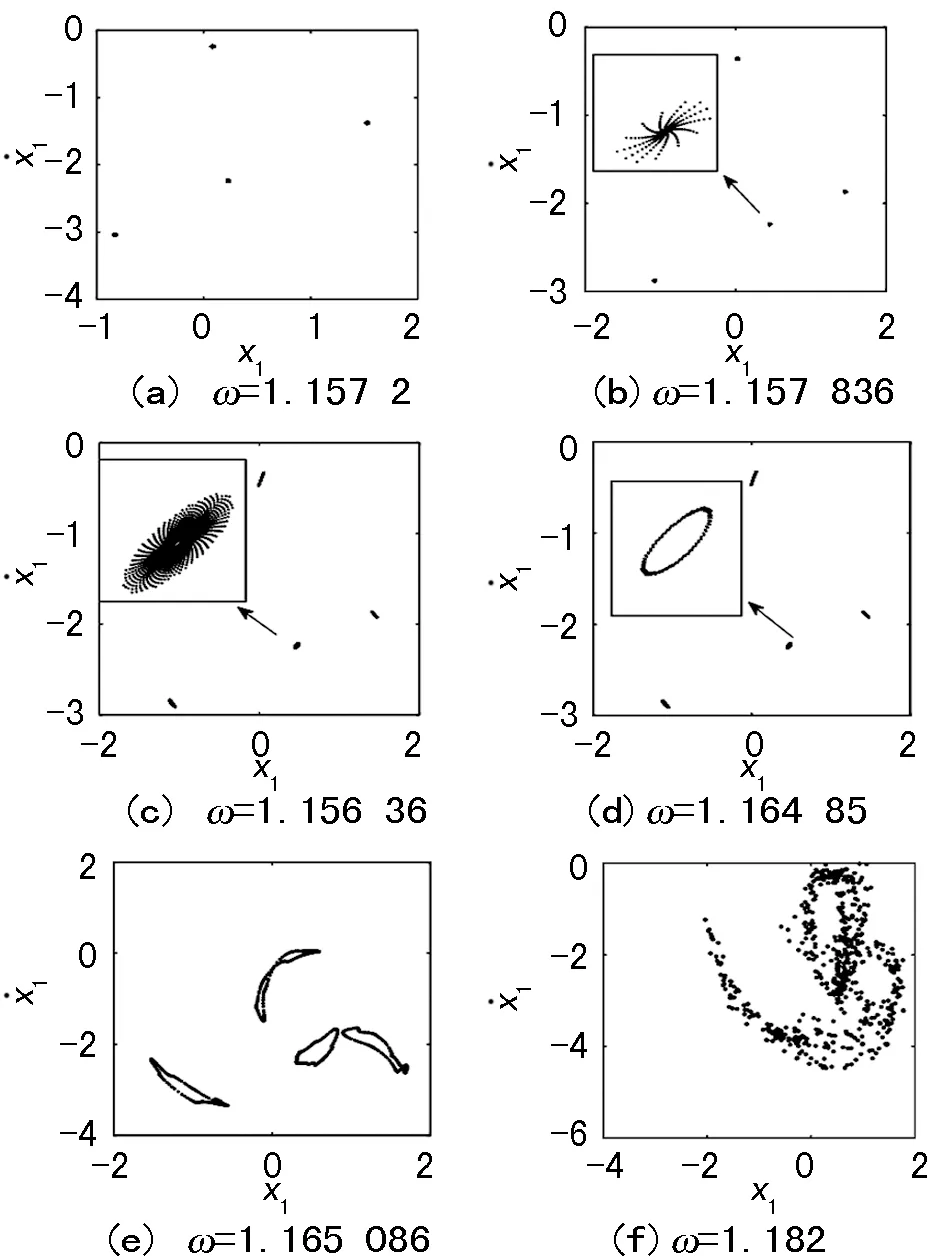
图3 Poincaré映射图一

当ω处于1.165 8和1.218时，系统绝大多数处于混沌运动状态，其中也出现了2个狭窄的周期运动窗口。当ω穿越1.220 08后，退出混沌，并出现逆倍化分岔，即发生混沌→q=4/2周期运动→q=2/1周期运动；随着ω的继续增加，导致系统经Feigenhaum倍周期序列通向混沌，当ω=1.267 5时，系统再次进入混沌，即发生q=2/1周期运动→q=4/2周期运动→q=8/4周期运动→q=16/8周期运动→混沌，如图4(a)～(d)所示。

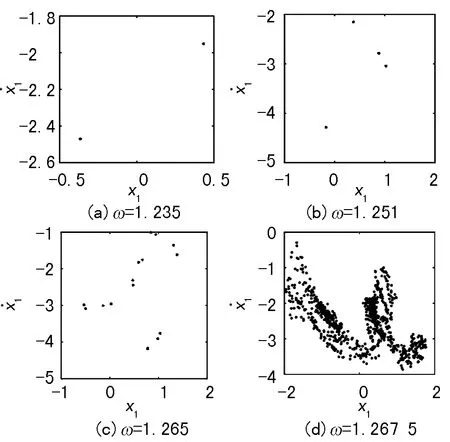
图4 Poincaré映射图二

经过第二次的混沌带后，系统退化出q=8/4周期运动，在ω从1.288～1.373 4的范围内，系统为q=8/4周期运动→q=4/2周期运动→q=2/1周期运动→q=1/1周期运动，并在相对较宽的区域内处于q=1/1运动；当ω穿越1.373 45后，出现q=17/10周期运动和q=18/10周期运动，分别如图5(a)、(b)，这是因为发生了“擦边分岔”，导致系统的Poincaré映射不连续，产生了奇异性。

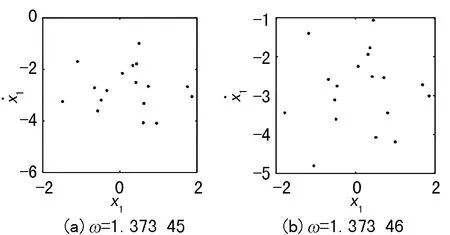
图5 Poincaré映射图三

(2) 阵发混沌分析

改变系统参数(1)，使得碰撞间隙d=0.30，编程得到系统的局部分岔图。图6是ω∈[1.345,1.395]之间的局部放大图。

图6 局部分岔图二

之前的几种分岔行为，都是由周期运动向混沌缓慢过渡。但系统还会发生另外一种分岔，即在周期运动和混沌运动之间发生了跳跃。图7显示了碰撞系统发生阵发性混沌的过程。

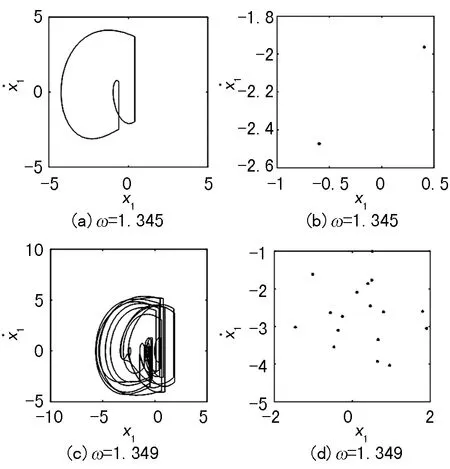
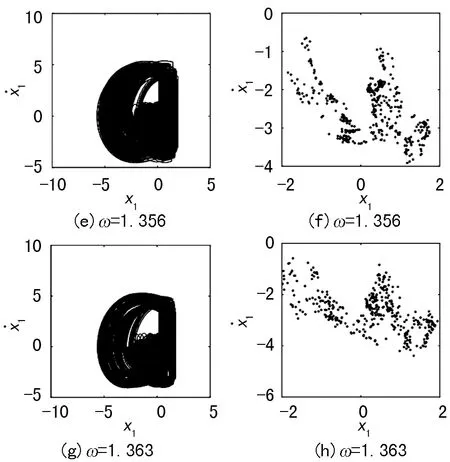
图7 相图和Poincaré映射图

当ω=1.345时，系统为q=2/1周期运动，如图7(a)、(b)；当ω∈[1.346,1.355]时，进入了混沌，如图7(c)、(d)；继续增加ω时，出现q=17/10周期运动，如图7(e)、(f)；ω继续增加至1.363时，再次进入混沌，如图7(g)、(h)；继续增加ω，碰撞系统的动态特性总是在周期运动与混沌之间来回不停跳变，发生阵发混沌。

4 减振器质量对车辆的稳定性影响

系统为多参数系统，影响车辆稳定性的因素有很多。现选择不同质量的减振器，从宏观上分析不同质量的减振器对车辆稳定性的影响。

当μm2=0.5，d=0.30，ζ1=0.01，ζ2=0.01，ζ3=0.02，ζ4=0.02，ζ5=0.02，υ1=1，υ2=2，υ3=0.5，υ4=0.5，υ5=1，θ=π/12，ω∈[1.15,1.55]时，系统在不同质量减振器μm1下的局部分岔图如图8所示。

图8 多参数局部分叉图

可见，不同质量的减振器对车辆的稳定性具有很大影响。下文将以μm1=0.13为参考基准进行分析比较。低频时，系统虽都表现为混沌运动，但增大或减小减振器质量都会导致车辆在混沌区域的运动幅值增大；当ω在1.28的一段邻域时，减小μm1系统也会进入混沌，但区域宽度相对有所减小，并且接下来的较大一段频率范围内，系统都将呈现为周期运动，稳定性改善。此时增大μm1系统则不会进入混沌，反而转化成了周期运动，稳定性改善；当ω>1.35时，系统在大多数频率下都呈现混沌运动，同时也出现了不同的周期窗口。此时可以看到，μm1越大，混沌区域越大，μm1越小，混沌区域越小。但系统处于混沌运动状态时，系统稳定位移的幅值与μm1的关系不大，三者大小基本保持一致。

现用同一频率下的相图、时间历程图和Poincaré截面图对系统做进一步分析。

当ω=1.414时，车辆系统在不同减振器作用下的相图、时间历程图和Poincaré映射图各不相同，如图9。当μm1=0.13、0.2时系统做混沌运动，当μm1=0.1时系统做q=1/1周期运动。可得在同一频率，不同质量的减振器可能会导致混沌、周期运动或者其他不同形式的运动同时出现。

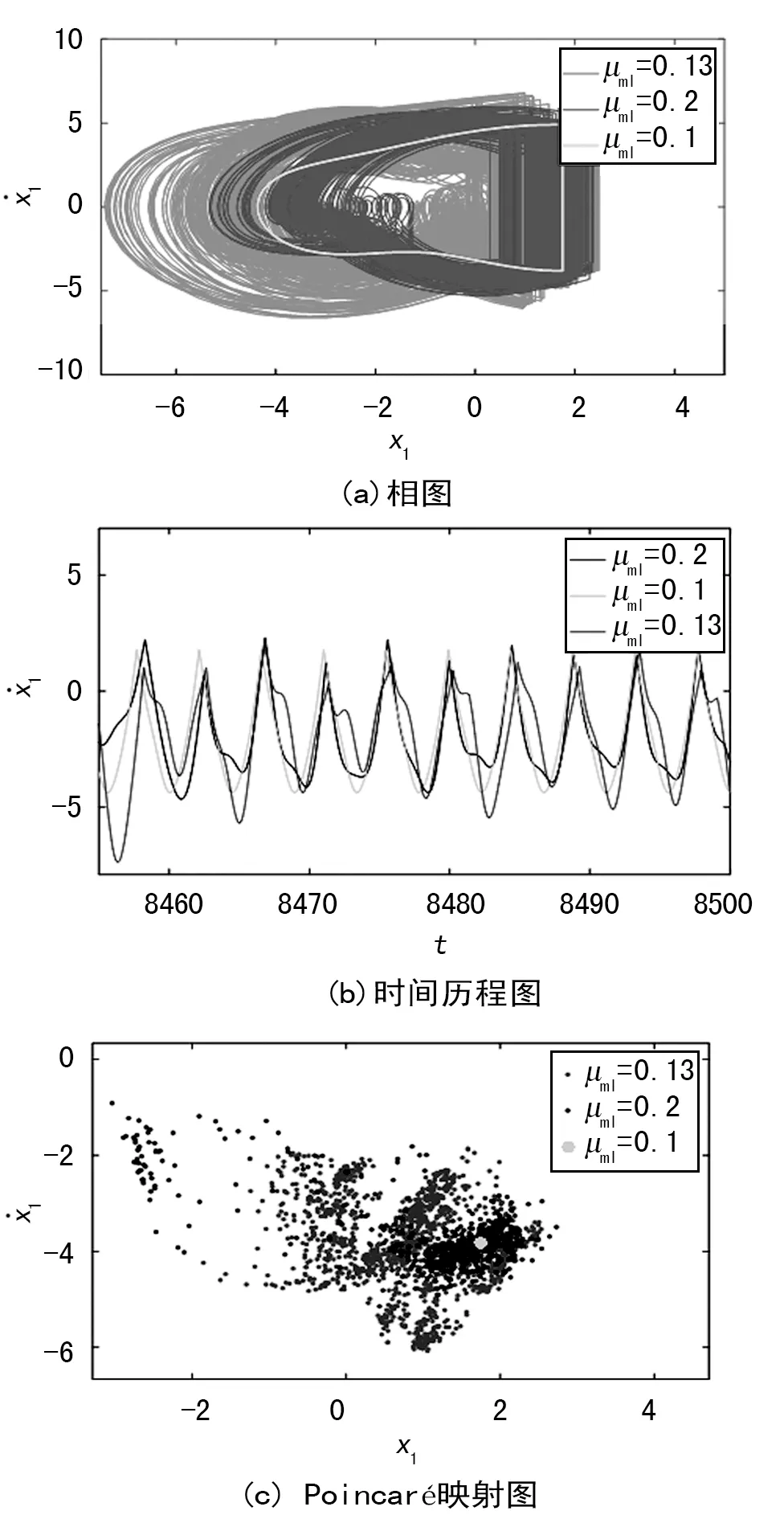
图9 ω=1.414时系统的响应图

同一频率下车辆运动的最大位移与最大速度常常作为衡量稳定性的重要指标之一。分析系统的最大位移与最大速度，可以得到不同频率下车辆运行相对稳定的减振器质量与车辆质量之比。

不同质量的减振器对车辆系统在一定频率范围内的最大位移与最大速度的影响情况如图10所示。

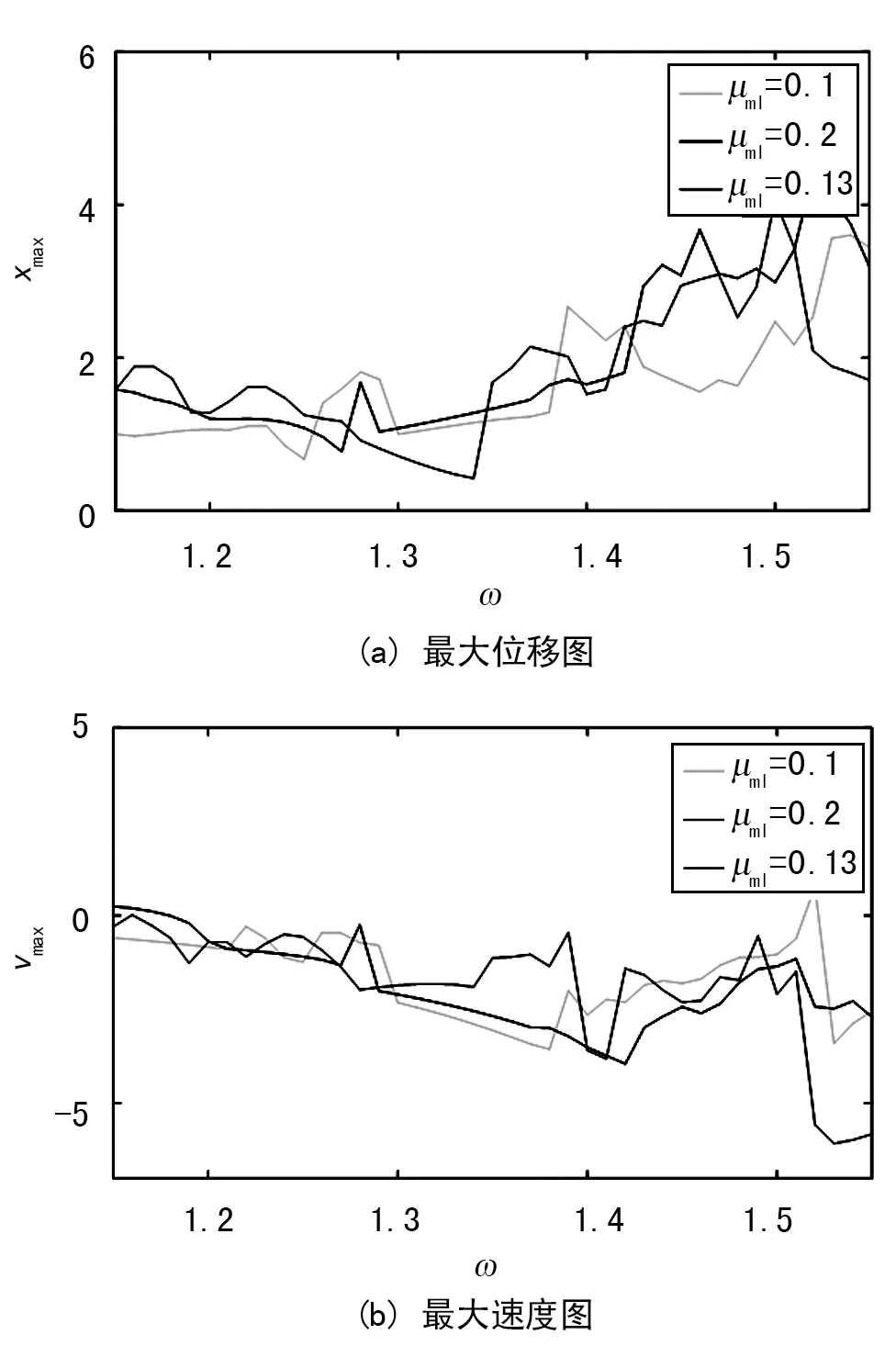
图10 不同减振器下的最大位移与最大速度图

当ω<1.23时，减小μm1，即减少减振器质量，车辆的最大位移相对最小，最大速度的变化也比较平稳，车辆稳定性很好。说明在相对低频状态下，减振器质量小，系统会更加稳定；当ω在1.28的较小领域内时，增大或减小减振器质量都会导致车辆的最大位移与最大速度出现局部极值，不稳定因素变强；当ω超过1.35后，系统的动态特性明显变得复杂，这从另一个方面证明车辆系统即将进入混沌运动状态。进入混沌区之后，较小质量的减振器有较小的最大位移的最大速度。同时，在混沌区域当中，不同减振质量下的车辆系统都频繁出现最大位移与最大速度的峰值，危险很大，这在工程设计优化当中应该尽量避免。

可见，为了提高车辆的安全性与舒适性，在不同的频率范围下应选择不同质量的减振器，即工作在不同工况下的车辆应该选装不同质量的减振器。

5 结 论

(1) 文中建立了车辆斜碰模型，建立运动微分方程，通过相图、时间历程图和Poincaré映射图研究了车辆斜碰撞系统，发现会出现倍化分岔、逆倍化分岔、hopf分岔、跳变、周期运动、混沌和阵发混沌。

(2) 通过仿真得到不同质量减振器对车辆系统运动行为影响的局部分岔图，得到减振器是车辆稳定性的重要影响因素，在不同的频率下不同车辆有不同的最优选择。

(3) 车辆在不同质量减振器、同一频率作用下可能会出现周期运动、混沌或其它非线性行为。

(4) 通过分析不同质量减振器作用下的最大位移和最大速度，从非线性动力学的角度分析得到不同工况下的车辆应选择不同的减振器。

(5) 为相似的斜碰撞研究提供借鉴经验。