放射性气溶胶净化装置中集尘罩的设计仿真分析*

李全兴，雷泽勇，钟 林，招观荣

(南华大学 机械工程学院，湖南 衡阳 421001)

0 引 言

核设施在运行、维护、退役过程中会产生大量放射性污染废金属。核废金属材料主要为碳钢和不锈钢，一般情况，受污染金属表面腐蚀的氧化层中存在≥98%的放射性核素(钴60、钴58、铬51、镍63、铁55等)，只有低于2%的放射性核素存在于金属表层0～10 μm处，在10 μm以下只有低于0.1%的放射性核素存在[1-2]。

采用干冰喷射去除金属表面放射性污染的原理是通过压缩空气将干冰颗粒加速，经喷嘴打到需要去污的金属表面，将金属表面带有绝大多数放射性污染的氧化层剥离，以此来达到去污的目的[3]。干冰颗粒会将碳钢表面铁锈及其它沉积物冲散成微小的颗粒，从而在空气中形成气溶胶。如果不对这些气溶胶进行及时处理，不仅会对现场工作人员的健康产生危害，同时也会对周边环境产生污染。

有大量学者对室内颗粒物的分布规律展开了研究。其中Tsang-Jung Chang等[4]建立了一个三维拉格朗日粒子跟踪模型，并通过实验探讨空气颗粒物在室内分隔环境中的传输机制，结果表明，粒径大于1 mm的颗粒运动主要受阻力和惯性力的影响，粒径小于0.5 mm的颗粒运动主要受布朗运动力的影响，对于粒径为2.5～5 mm的特定范围内，Saffman升力不能忽略。另有大量研究人员对气溶胶收集装置进行设计，张文俊等[5]设计了一套放射性松散污染真空吸尘装置，将收集到的污染物经旋风分离、滤袋过滤、高效过滤三级分离后，对污染物进行有效收集，从而使尾气达到核级排放标准。

笔者利用ANSYS FLUENT软件对集尘罩吸收放射性气溶胶的过程进行数值模拟，并通过MATLAB软件对数值模拟结果进行回归分析，得到集尘罩最优结构。

1 研究方法与原理分析

1.1 仿真流场概述

在FLUENT软件中的DPM模型的计算过程中，以欧拉-拉格朗日方法为基础，将主相空气视为连续相，次相铁锈颗粒视为离散相，各相性质始终稳定。连续相基本方程组中的质量守恒方程和动量守恒方程分别可表示为[6-7]：

(1)

ραg1+F1

(2)

式中：α为连续流体相的体积率；ρ为流体相密度；p为静压；vi为流体在i方向上的流速分量；gi为坐标i方向上的体积力；τij为黏性应力张量；Fi为连续相与离散相的相互作用力。

在DPM模型中是通过拉格朗日参考系中的运动方程来计算离散相颗粒的运动轨迹的。以直角坐标系内x方向为例，离散相颗粒运动方程为[8]：

(3)

式中：u为连续相在x方向的速度；ρ为连续相在x方向的密度；up为离散相颗粒在x方向的速度；ρp为离散相颗粒在x方向的密度；fD(u-up)为单位质量颗粒受到的阻力。

其中fD的表达式为：

(4)

式中：CD为阻力系数；Rep为颗粒相对雷诺数。

1.2 颗粒受力分析

流场中的颗粒主要为铁锈和灰尘颗粒，除了受到重力和浮力的合力作用外，还受到其它各种力的作用，不同的力对运动中的颗粒作用不同，因此处理方式也不同[8-9]。

颗粒的阻力大小受多种因素的影响，如颗粒的相对雷诺数、流体的可压缩性、颗粒温度等，为便于研究，引入阻力系数的概念，阻力Fr可以定义为：

(5)

式中：Cparticle为颗粒阻力系数，颗粒阻力系数受众多因素影响，包括颗粒形状、颗粒雷诺数等。

当颗粒在存在压力梯度的流场中运动时，由压力梯度对颗粒产生的力，即压力梯度力，其表达为：

Fp=-Vpgradp

(6)

式中：Vp为颗粒的体积，当小粒子的存在不影响流体的流动时，可近似认为：

(7)

则压力梯度力又可表示为：

(8)

流场中的颗粒因为旋转会产生升力，称为Magnus升力，表示为：

(9)

式中：ω为颗粒旋转速度，实际上对于大多数粒子需要引入试验系数k来修正：

(10)

当颗粒在流场中运动且上部的速度大于下部的速度时，上部的压力小于下部的压力，颗粒受到向上的升力，称为Saffman升力，当颗粒的相对雷诺数Rep<1时，其表达式为：

(11)

当Re比较大时，Saffman升力没有对应的计算公式。由式(11)可以看出，Saffman升力的大小与速度梯度du/dy有关，在流场的主要流动区域速度梯度很小，此时的Saffman升力可以忽略不计。

当颗粒在流场中做加速运动时，此时的颗粒质量被虚拟地增加，这部分增加的质量称为虚拟质量力。在这种情况下，单个颗粒所受的虚拟质量力为：

(12)

单位质量颗粒所受的虚拟质量力为：

(13)

当ρ≪ρp时，虚拟质量力可忽略不计。

颗粒在黏性流体中做直线运动时，既要受到黏性阻力和虚拟质量力，同时还会受到一个瞬时流动阻力，即Basset力。其表达式为：

(14)

式中：μ为流体的黏性系数；t为总时间。

气固两相流模型中离散相颗粒所受的力的种类繁多，在对其进行计算时需对其所受的力进行有效取舍。总的来说，一般颗粒受到的阻力最大，约比颗粒所受重力大1～2个数量级，比Saffman升力和虚拟质量力大3～4个数量级。在DPM模型中，一般不考虑Basset力，因为Basset力只在加速初期产生，而文中研究的是流场稳定状况。而对于Magnus升力，DPM模型将颗粒视为光滑的球形，不会产生较大旋转，因此Magnus升力也可以忽略不计。

2 相关参数及试验方法

2.1 风机选择

在进行流场仿真分析之前，需要根据集尘罩和风管结构来选择风机，并最终确定负压大小。由于设备限制和操作环境要求，采用上吸式集尘罩，气流只能从集尘罩下方流入罩内，其结构参数如图1所示，其中α为集尘罩扩张角。

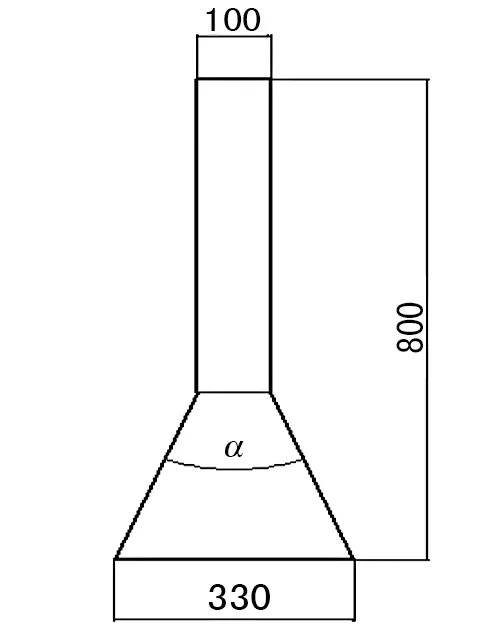
图1 上吸式集尘罩

根据文献[10]，其排风量的计算公式为：

L=KPHvx

(15)

式中：K为沿高度速度分布不均匀的安全系数，通常取为1.4；P为排风罩口周长，文中取罩口直径为300～350 mm时进行研究，计算排风量时应按最大直径d=350 mm时进行计算，P=πd=1.1 m;H为罩口到污染源的距离，受壁面横向气流影响，H应小于或等于0.3d，即H≤0.3d=0.1 m;vx为边缘控制点的控制风速，在这里取为0.9。

运用式(15)可得，L=0.14 m3/s=504 m3/h，考虑到管路的漏风和计算结果不精确等因素，应按下式计算结果来选择风机：

Lf=KL·L

(16)

式中：KL为风量附加系数，在这里取为1.15；Lf=KL·L=580 m3/h。因此，选取型号为DF-1.6-Ⅱ的离心风机，其参数如表1所列。

表1 DF-1.6-Ⅱ型离心风机参数

根据流量Q=660 m3/h=0.18 m3/s，管径D=100 mm，由通风管道单位长度摩擦阻力线算图[10]可得摩擦阻力Rm0=70 Pa/m，流速v=22 m/s。应用管壁粗糙度修正公式对摩擦阻力进行修正：

Rm=KtRm0

(17)

Kt=(Kv)0.25

(18)

由于使用的是薄钢板，K取0.18，Rm=98.7 Pa/m，假设管道长度为2 m，损失压力为197 Pa，负压取值为653 Pa[10-11]。

由工业通风一文中得知[10]，当集尘罩扩张角为40°左右时，局部阻力系数最小，不同扩张角时集尘罩罩口中心速度vc和平均速度v0的比值如表2所列，此比值反映集尘罩气流的均匀程度。

表2 不同扩张角的速度比

综合局部阻力系数和速度比，当扩张角α=30°～50°时，阻力最小，且集尘罩内气流较均匀。影响集尘罩吸尘效果的因素主要为扩张角和罩口直径，吸尘效果以颗粒通过出口时的时间来反映，文中采用均匀设计法对吸尘效果进行研究[12-13]，扩张角α取30°～50°，罩口直径d取300～350 mm。

2.2 试验方法

均匀设计方法只考虑试验点在试验范围内的均匀分散性，而忽略了整齐可比性，其优势在于减少了试验次数，但缺点是无法直接分析试验结果，需要用回归分析的方法对结果进行分析。文中设置了2个因素，每个因素设置了6个水平[14]。如表3所列。采用U6(64)均匀设计表来确定各组试验参数取值，如表4所列。

表3 各因素对应水平

表4 分组试验取值

3 仿真及结果分析

3.1 均匀设计试验

以集尘罩作为流场研究对象，使用SolidWorks软件按如图2所示尺寸参数对其进行建模。以扩张角α=30°，d=350 mm时的集尘罩为例，利用ANSYS-ICEM软件对集尘罩进行结构化网格划分，定义其全局最大网格尺寸为0.02，对集尘罩壁面部分进行网格加密，壁面第一个网格节点距离设为0.004，变化率为1.05，最终划分出的网格如图3所示。

图2 集尘罩建模图 图3 网格划分

利用FLUENT软件对其进行仿真分析，集尘罩中的气流流动属于高雷诺数的湍流流动，不属于强旋流或弯曲壁面流动，因此，连续相选用标准的k-ε模型，该模型能很好地模拟流场速度，标准k-ε方程为[15]：

=τtijSij-ρε+Øk

(19)

(20)

式中：μt为涡粘性，其表达式为μt=Cμfμρk2/ε；Sij为平均速度应变率张量；ρ为流体密度；k为湍动能；各常数的取值为Cμ=0.09，cε1=1.45，cε2=1.92，σk=1.0，σε=1.3。

出口处负压值设为计算得出的653 Pa，DPM模型中颗粒为FLUENT颗粒材料数据库中自带的钢铁粉末，颗粒类型为惰性颗粒，注入类型为从入口注入，干冰喷射后使颗粒具有入射速度，为便于研究，取入射速度为0.5 m/s，颗粒粒径取为50 μm[16]。按照以上条件对集尘罩流场进行仿真分析，得到结果如图4所示[17]。

图4 流场分析结果

由图4可见，压力多集中在集尘罩罩口位置，高度越往上压力越小，速度分布较规整，大多数颗粒速度方向都由入口指向出口，无涡流，能量损耗比较小。

依照表4试验分组参数进行仿真分析，6组试验得到的结果如表5所列。

表5 试验结果

3.2 结果分析

通过仿真分析得到扩张角和罩口直径对颗粒逃逸时间的影响，分别如图5(a)、(b)所示[18]。

图5 两因素分别对集尘效果的影响

令α为x1，d为x2，t为Y，利用MATLAB软件对试验结果进行回归分析[19]，执行程序后得到Y的多元线性回归参数，如表6所列。

表6 Y的多元线性回归参数

回归方程置信度R2=0.535 9，F=1.732 1，P=0.316 2>P0=0.05，为不显著，即多元线性回归不适用该试验结果，需要对其进行多元非线性回归分析，多元非线性回归分析方程为[20]：

(21)

式中：a为常数项；b为各项系数。

在MATLAB中进行多元非线性回归分析，结果如图6所示，对其中数据进行导出，结果如表7所列。

图6 多元非线性回归结果图

表7 导出数据

beta值代表回归分析方程中对应的数值，rmse值为均方误差，其值越小，表明拟合越好。因此，该回归方程为：

Y=-586.341 1-1.853 8x1+3.965 7x2+

(22)

根据此回归方程，在x1=46,x2=350时；Y取最小值，最小值可以直接在MATLAB软件中得出，如图7所示，Y的最小值为0.100 6，即此时颗粒逃逸集尘罩出口所需时间最短，为0.100 6 s。

图7 Y的最小值

4 结 论

针对放射性气溶胶净化装置中集尘罩的设计，通过均匀设计试验与回归分析，得出以下主要结论。

(1) 对集尘罩排风量进行计算，得到其排风量约为580 m3/h，按照此排风量来选择风机，最后按风机参数计算集尘罩出口负压取值。

(2) 按照均匀设计试验法设计了6组试验，两个因素取为集尘罩的扩张角和罩口直径，以颗粒逃逸出集尘罩出口的时间来反映集尘罩的集尘效果，利用FLUENT软件对6组试验分别进行仿真分析。

(3) 利用MATLAB软件对试验结果进行回归分析，得到回归方程，并依照此回归方程，得出当扩张角为46°，罩口直径为350 mm时，颗粒逃离集尘罩所需时间最少，故此结构为该工况下的最优集尘结构。

此次研究得到该工况下集尘罩最佳结构参数，对各类除尘装置中集尘罩的设计具有一定参考意义。