大档距/高差线路非均匀覆冰下的脱冰跳跃特性研究

(西南交通大学电气工程学院，四川 成都 610031)

0 引 言

输电线路覆冰事故一直是电力系统严重的自然灾害之一[1-3]。远距离输电线路难免会跨越高山、峡谷/大河区。对于大高差爬山线路，由于海拔的影响，线路档内的覆冰往往呈现覆冰厚度随海拔递增的趋势。对于跨越峡谷/大河的大档距线路，由于环境中风速、湿度和空气中液态水含量等环境因子分布不均匀，导致导线在覆冰时可能出现覆冰厚度沿档距分布不均的现象。据统计[4-5]，线路90%以上的断线和倒塔是由于微地形、微气象下引起非均匀覆冰以及档距、高差过大等因素引起的纵向不平衡张力造成的。由于微地形、微气象因素的影响引起线路不均匀覆冰，2011年1月，国网四川省电力公司500 kV布坡线4回线路全部跳闸停运。因此为保障重冰区输电线路的安全运行，亟需开展输电线路脱冰跳跃动力特性的研究。

国内外学者对覆冰导线脱冰跳跃特性已开展了广泛的研究[6-8]。文献[9]最先将覆冰和冰脱落等效为集中载荷来模拟实现。文献[10]在国内最早利用均匀分布在导线上若干点处的集中载荷来模拟覆冰。文献[11]基于相似性理论，提出用于模拟导线脱冰跳跃的缩比模型试验方法，并与真型线路脱冰试验对比验证了方法的正确性，为输电线路的脱冰跳跃研究提供了新思路。文献[12]研究发现不均匀脱冰对绝缘子串张力影响显著，其瞬态值达导线初始张力2倍多。文献[13]建立了三自由度多档导线运动模型，结果表明随机非均匀脱冰跳跃幅值最大点并不一定在脱冰档中点。文献[14]利用有限元方法对均匀覆冰线路脱冰后的动力响应进行了参数研究，并提出了计算最大脱冰跳跃高度的简单公式。以上研究均只考虑均匀覆冰，即均假设冰载荷在一档内均匀分布，现有设计规范[15]也只考虑均匀覆冰。下面采用有限元法建立线路脱冰跳跃模型，针对大档距和大高差线路两种典型的非均匀覆冰形式，研究档距、高差、覆冰厚度等因素对脱冰跳跃特性的影响。基于非均匀覆冰导线脱冰计算分析结果，对现有脱冰跳跃经验公式进行改进。

1 分裂导线有限元模型

1.1 有限元模型

采用3跨连续档四分裂导线作为研究对象，导线型号为LGJ-400/35，其参数如表1所示。由于输电线路杆塔的变形对导线脱冰跳跃的影响很小[16]，所建立的有限元模型忽略输电杆塔刚度的影响，有限元模型包含导线、绝缘子串、间隔棒和线夹等典型部件，如图1所示。其中：导线采用只能承受拉伸不能承受压缩的索单元模拟，在Abaqus软件中可以通过设置空间杆单元的材料性质来模拟索，导线单元长取0.5 m可以满足单元收敛性要求[17]；间隔棒和线夹简化为框架，其密度根据实际间隔棒重量来计算确定，采用梁单元进行模拟；悬垂绝缘子串简化为直杆，与杆塔连接处释放转动自由度，仅约束3个平动自由度，以模拟脱冰跳跃过程中能量在不同档间的相互传递。

表1 LGJ-400/35导线物理参数

阻尼是动力学特性的一个重要参数，但输电导线阻尼的精准确定十分困难。针对脱冰跳跃问题，已有研究表明阻尼会影响导线脱冰跳跃动力特性，但其对导线脱冰后第一个峰值(脱冰跳跃高度)影响很小[14]。参照文献[18]，采用瑞利阻尼模型，阻尼比取值2%。

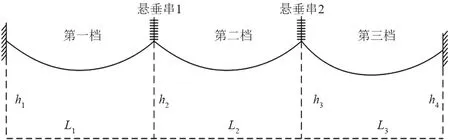
图1 计算模型

1.2 覆冰载荷的模拟

当导线上承受覆冰载荷作用时，导线上的载荷包括自重载荷和覆冰载荷。为了简化覆冰过程，提高计算效率，采用改变导线的重力加速度来模拟覆冰过程[11]。导线覆冰后的等效密度可以通过式(1)计算。

(1)

式中：ρ1为导线单位长度密度，kg/m3；w1为导线单位长度重量，N/m；ρ2为导线单位长度覆冰密度，kg/m3；w2为导线单位长度覆冰重量，N/m；A为导线截面面积，m2；g为重力加速度。

为了模拟导线非均匀覆冰，将导线均匀分割成200小段，通过设置每段的覆冰载荷模拟非均匀覆冰形式。均匀覆冰如图2(a)所示，即档内覆冰厚度相同。针对线路大档距和连续爬坡线路区段设置了两种典型的非均匀覆冰方式，如图2(b)和图2(c)所示，其中小黑原点越大表示覆冰越厚。设非均匀覆冰档导线的长度为L，直径为D，则导线在非均匀覆冰时每段的覆冰质量mi和总质量M可表示为：

mi=ρiceπbni(bni+D)li

(2)

(3)

式中：mi为第i段导线的覆冰质量，kg；bni为第i段导线的覆冰厚度，mm；li为第i段导线的长度，m；ρice为覆冰密度，kg/m3；D为导线直径，m；M为导线覆冰总质量，kg；N为导线分段数。

为了对比均匀覆冰和非均匀覆冰下脱冰动力特性的差异，采用控制单一变量的方法。无论是均匀覆冰还是非均匀覆冰，假设控制档内的覆冰总重量相同。先计算非均匀覆冰形式下档内的覆冰总重量，然后可通过式(4)计算均匀覆冰形式的覆冰厚度bu。

(4)

式中：bu为均匀覆冰时的覆冰厚度，mm；L为导线长度，m。

1.3 脱冰载荷的模拟

导线的密度保持不变，通过改变惯性加速度来实现脱冰过程的有限元模拟。此时脱冰档导线的惯性加速度可表示为

(5)

式中：ge为脱冰档导线脱冰前的等效惯性加速度；μ为导线的脱冰率。当导线脱冰时，更改惯性加速度ge即可实现导线部分覆冰的脱落。

1.4 数值模拟验证

为了验证所提数值模型的正确性，利用真型五档线路[19]的结果进行验证，真型线路的档距为283 m、387 m、247 m、213 m和309 m，其高差分别为5 m、16 m、28 m、16 m和8 m。导线直径为19.6 mm，单位长度质量为0.85 kg/m，截面积为227.6 mm2，杨氏模量为91 800 MPa。分别开展真型线路在1.49 kg/m、2.98 kg/m、4.47 kg/m、5.96 kg/m不同覆冰载荷下的脱冰试验，并得到其最大脱冰跳跃高度。此外文献[20]也用有限元方法模拟了相应的脱冰过程，并得到其最大脱冰跳跃高度。将数值模拟结果与真型线路试验结果以及文献[20]的数据进行对比，结果如图3所示。可以看出，最大脱冰跳跃高度随着脱冰冰量的增加而增加，数值模拟结果与真型试验结果最大误差为7%。这可能是因为有限元模型中导线的阻尼比与实际导线的阻尼比存在一定的差异导致的。

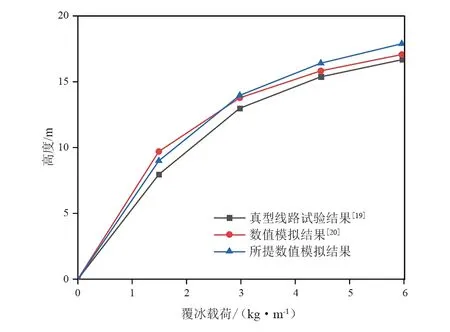
图3 真型试验线路和数值模型得到的最大脱冰跳跃高度

图4 脱冰跳跃高度的定义示意

图5 档距对最大脱冰跳跃高度的影响

2 非均匀覆冰导线的脱冰跳跃计算

2.1 导线脱冰跳跃高度的精确定义

现有研究[12-14]只考虑导线均匀覆冰，脱冰跳跃后档距中点反弹的脱冰跳跃高度最大，定义其为最大脱冰跳跃高度。当考虑非均匀覆冰时，覆冰厚度在档内存在差异，此时，导线脱冰跳跃最大高度不一定在档距中点。此外，由于导线和地线的弧垂存在差异，当研究脱冰跳跃导致的导线与地线的绝缘间隙裕度问题时，导线的最大脱冰跳跃高度及其在档内所处的位置同等重要。

对此，分别提取脱冰档导线沿档各点的最大脱冰跳跃高度，构成脱冰跳跃高度曲线，如图4所示。该图可以直观反映脱冰档不同位置的最大脱冰跳跃高度的变化情况。其中，导线脱冰跳跃高度最大值所在档内的位置定义为Pmax，其表示为脱冰跳跃高度最大值的位置(到端部的距离)与档距的比值。

2.2 导线脱冰跳跃高度

基于上述有限元模型及覆冰和脱冰模拟方法，对输电线路脱冰跳跃高度进行分析。对于大高差、大档距线路，根据应力弧垂表确定导线初始张力。研究对象为3档四分裂导线，脱冰档位于第二档，如图1所示。这里主要针对导线非均匀覆冰与均匀覆冰下，数值模拟得到导线最大脱冰跳跃高度与各种参数之间的关系，参数有档距、高差、覆冰厚度、导线的初始张力等。

1)档距的影响

采用单因素控制变量法，研究脱冰档的档距分别为400 m、600 m、800 m、1000 m时导线最大脱冰跳跃高度的变化规律。第一档和第二档的档距均为100 m，无高差，脱冰率为100%，则不同档距下的最大脱冰跳跃高度如图5所示。其中，不同档距下导线初始张力分别为30.42 kN、29.89 kN、29.70 kN、29.62 kN。

由图5(a)可见，随着档距的增加，最大脱冰跳跃高度呈现逐渐减小的趋势。最大脱冰跳跃高度与非均匀覆冰密切相关，随着档距的增加，非均匀覆冰对最大脱冰跳跃高度的影响越强烈。由图5(b)可见，最大脱冰跳跃高度随着档距的增加先增大后减小，在档距为600 m时最大脱冰跳跃高度达到最大值，非均匀覆冰对最大脱冰跳跃高度的影响相对较小，但对发生最大脱冰跳跃高度的位置影响较大；随着档距的增大，发生最大脱冰跳跃高度的位置逐渐向档距端部靠近，档距为1000 m时，发生最大脱冰跳跃高度位置Pmax为0.26。

2)高差的影响基于3档四分裂线路模型(档距为100 m—600 m—100 m)，采用单因素控制变量法，研究脱冰档高差分别为50 m、100 m、150 m、200 m下导线的最大脱冰跳跃高度的变化规律。不同高差下导线最大脱冰跳跃高度如图6所示，其中导线的初始水平张力为29.89 kN。由图6(a)可得，对于大档距线路，高差对最大脱冰跳跃高度的影响相对较小，非均匀覆冰下的最大脱冰跳跃高度与均匀覆冰下的最大脱冰跳跃高度相差基本保持在38%左右。

由图6(b)可得，最大脱冰跳跃高度随着高差的增大而减小，非均匀覆冰对最大脱冰跳跃高度的影响较大。

3)覆冰厚度的影响

为了进一步研究覆冰厚度对最大脱冰跳跃高度的影响，根据3档四分裂线路模型(档距为100 m—600 m—100 m)，大档距线路无高差，大高差线路的高差为200 m，采用单因素控制变量法，分析覆冰厚度为13 mm、18 mm、23 mm、28 mm时导线的最大脱冰跳跃高度变化情况。不同覆冰厚度下导线最大脱冰跳跃高度如图7所示，其中不同冰区下导线的初始张力分别为56.72 kN、42.70 kN、32.74 kN、26.84 kN。

由图7可得，随着覆冰厚度的增加，最大脱冰跳跃高度也在逐渐增大，且非均匀覆冰下的最大脱冰跳跃高度始终大于均匀覆冰下的最大脱冰跳跃高度。对于非均匀覆冰下的大高差线路，最大脱冰跳跃高度发生的位置并不在档距中点。综上，非均匀覆冰下的最大脱冰跳跃高度更容易引发闪络事故，因此实际工程中进行线路校验时，应考虑导线非均匀覆冰的状况。

图6 高差对最大脱冰跳跃高度的影响

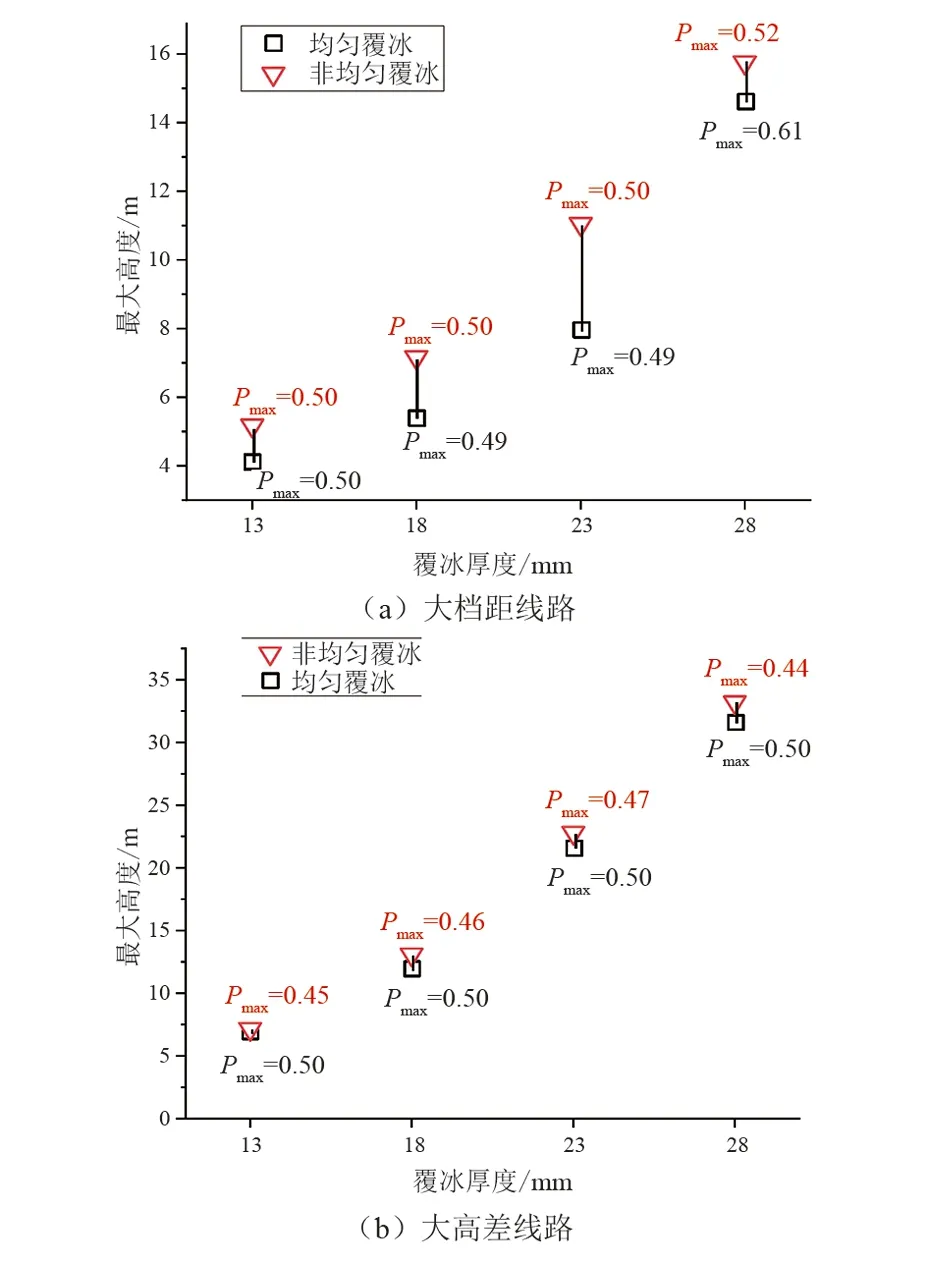
图7 覆冰厚度对最大脱冰跳跃高度的影响

3 经验公式改进进行

有效预测导线脱冰跳跃高度可对线路设计提供可靠的依据。研究者们根据实验和数值模拟结果进行了总结并得出了计算脱冰跳跃高度的经验公式。下面以非均匀覆冰的模拟结果作为依据，对常见的经验公式进行误差分析并加以改进。

3.1 经验公式误差分析

目前常用的经验公式为中国输电线路设计规程[15]利用前苏联的计算公式。

H=(2-l/1000)Δf

(6)

式中：H为导线最大脱冰跳跃高度，m；l为档距，m；Δf为导线脱冰前后静止状态的弧垂之差，m。文献[14]对式(6)进行了简化，为

H=1.82Δf

图8 式(6)、式(7)与仿真结果相对误差

(7)

以上各经验公式均能预测导线脱冰跳跃高度，但没有考虑非均匀覆冰对脱冰跳跃高度的影响，因此提出以非均匀覆冰导线脱冰跳跃的有限元结果作为依据，对以上经验公式进行误差分析，其分析结果如图8所示。由图8可得，中国输电线路设计规程所用公式的误差可达55%以上。文献[14]提出的经验公式误差在35%以下，比中国输电线路设计规程所用的公式略有提高。

3.2 经验公式改进

由于上述公式都没有考虑非均匀覆冰对最大脱冰跳跃高度的影响，为进一步提高经验公式的泛化能力，引入非均匀覆冰影响系数对其进行适当改进。

由第2.2节分析可得，非均匀覆冰下的最大脱冰跳跃高度比均匀覆冰下的最大脱冰跳跃高度更大。因此，可以通过在式(6)中引入非均匀覆冰影响系数μ来提高其准确性，如式(8)所示。然后，基于非均匀覆冰下的脱冰跳跃结果采用最小二乘法进行拟合，得到改进后的公式如式(9)所示。

H=μ(2-l/1000)Δf

(8)

H=1.6(2-l/1000)Δf

(9)

针对档距600 m，覆冰厚度最大值分别为13 mm、18 mm、23 mm、28 mm的最大脱冰跳跃高度计算结果进行改进后的公式误差分析，如图9所示，可见最大相对误差在9%以内。非均匀覆冰更加严重时，式(9)具有更精确的预测效果。因此，大档距、大高差输电线路发生非均匀覆冰时，所提改进公式具有较好的预测能力，为输电线路设计提供参考。

图9 公式得到的脱冰跳跃高度

4 结 论

上面采用有限元方法探讨了非均匀覆冰导线的脱冰跳跃特性，分析了档距、高差、覆冰厚度等参数对最大脱冰跳跃高度的影响规律，基于数值模拟结果，考虑非均匀覆冰影响系数，对经验公式进行改进。其结论如下：

1)对比均匀覆冰，非均匀覆冰下发生脱冰跳跃后导线的最大脱冰跳跃高度更大。且最大脱冰跳跃高度所在位置可能不在档距中点，更容易引发闪络事故。工程设计应考虑非均匀覆冰对脱冰跳跃的影响。

2)大档距线路发生非均匀覆冰时，最大脱冰跳跃高度与非均匀覆冰密切相关，随着档距的增加，非均匀覆冰对最大脱冰跳跃高度的影响越强烈。大高差线路发生非均匀覆冰时，随着档距的增大，发生最大脱冰跳跃高度的位置逐渐向档距端部移动。

3)通过在脱冰跳跃高度经验公式中引入非均匀覆冰影响系数对公式进行改进，提高了经验公式的预测准确性，且其使用范围也更加广泛。