城市轨道交通工程GNSS控制网复测实施及稳定性分析
曲田,李晓峰
(中铁第六勘察设计院集团有限公司,天津 300031)
1 引 言
GNSS控制网作为城市轨道交通工程的首级控制网,是包括盾构施工、轨道施工在内整个工程的平面起算基准。控制网准确、稳定是确保隧道顺利贯通,轨道精确安装的前提,因此定期对其进行复测,及时对变化点位进行更新。目前针对城市轨道交通工程GNSS控制网复测主要存在以下两个方面问题:第一,坐标更新原则不明确。由于观测误差、仪器设备自身误差等的存在,控制网每期复测成果必然存在一定的差异,必须对其进行分析和研究,以判断控制点位置是真正变动还是由于测量误差所引起的变化,进而判断控制网是否稳定。[1]《城市轨道交通工程测量规范》中要求当复测与原测成果坐标分量较差的极限误差分别小于 2 m时(m为复测控制点的点位中误差),应采用原测量成果,大于 2 m时,应查明原因及时补测或者修测,并应满足与相邻控制点的相对点位中误差要求。随着测量技术的发展,GNSS接收机的精度和稳定性越来越高,控制网的复测精度不断提高,复测点位的中误差通常为毫米级,因此若大于 2 m就更新点位坐标,就会导致成果更新比例过高,不利于保持控制网的连续性;第二,出于保密等因素,GNSS控制网的建网单位在向施工单位或第三方测量单位移交控制网成果时通常不提供控制网的上一级起算点,需要在复测时选择合适点位作为起算点。点位的选择直接关系到整个控制网复测的精度,因此需要对选择的控制点进行稳定性分析。
本文以郑州市轨道交通8号线一期工程首级GNSS控制网复测为例,详细介绍了城市轨道交通GNSS控制网的布网形式、施测要求、数据处理流程、起算点稳定性分析并结合城市轨道交通工程特点提出坐标较差、边长较差加方位角较差的坐标更新原则。
郑州地铁8号线一期工程(以下简称8号线)作为郑州市城市轨道交通第三期建设规划中的骨干线路,呈东西走向,线路全长 51.495 km,跨越郑州市多个行政区。8号线一期工程GNSS控制网采用郑州城市坐标系,共包括65个点位(G801-G865)。
2 复测技术方案
2.1 复测精度指标
根据《城市轨道交通工程测量规范》[2]要求,线路控制网应在线路开工前进行复测,复测周期为1次/1~2年,并根据控制点稳定情况增加或减少复测频次。测量技术要求应符合表1要求:

表1 卫星定位控制网测量技术要求
卫星定位控制网基线长度精度应按下式计算:
(1)
式中:σ—基线长度中误差(mm);
a—固定误差(mm);
b—比例误差(mm/km);
d—相邻点间的距离(km)。
2.2 复测作业技术要求
复测过程中测量作业技术要求如表2所示:

表2 卫星定位控制网作业技术要求
2.3 复测网形设计
根据规范要求,并综合考虑控制网实际情况,复测网形设计需重点考虑以下几点:
(1)为确保短边间控制点相对精度,短边应设计在同一时段,测独立基线;
(2)综合考虑后期施工需要,盾构始发端与接收端控制点尽量设计在同一时段,测独立基线;
(3)充分考虑线路交叉处、同期建设其他线路控制网,控制点要有充分重合;
(4)根据施工需要,适当增减控制点,并纳入整网观测。
8号线GNSS控制网共计包括65个控制点(G801-G865),其中G801-G852为沿线路敷设指导施工的控制点,G853-G865为增强网形的配合点。经过控制点踏勘,根据实际情况变更点位4个,分别为G859变更为G859A、G860变更为G860A、G854变更为QSS10(14号线一期工程控制点)、G864变更为G726(7号线一期工程控制点);增加点位3个,分别为QSH32(10号线工程控制点)、XSQ、MZ,其中XSQ、MZ为多条线路共用的起算点。整个控制网共计包括68个点位,使用6台接收机,采用静态相对定位模式,以边连接或网连接,扩展成网,如图1所示。共设计30个同步观测时段,平均重复设站数2.65。
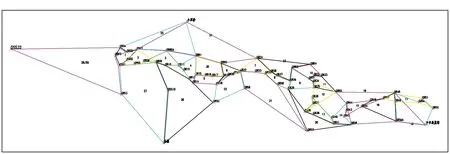
图1 郑州轨道交通8号线一期工程GNSS控制网复测时段图
3 复测实施
3.1 观测过程
外业观测采用6台拓普康Hiper V双频接收机(标称精度平面 3 mm+0.5 ppm;高程 5 mm+0.5 ppm),观测过程严格按照《城市轨道交通工程测量规范》中GNSS各项观测要求进行施测。此外,为提高观测质量,时段长度增加至 70 min,包含短边的时段观测时长增加至 90 min。
3.2 数据处理
GNSS控制网数据处理主要包括基线处理、三维无约束平差、约束平差及成果输出及分析等关键步骤。复测数据采用天宝TBC进行基线处理,采用CoasGPS进行网平差。
(1)基线处理
基线处理前,需要对数据进行预处理。第一,将从拓普康GNSS接收机中导出的原始观测转换成标准RINEX格式;第二,根据天线模型[3],将量取的仪高统一归算至仪器相位中心。基线向量解算采用多测站、多时段自动处理的方法[4]。基线解算时,长度小于 15 km的基线采用双差固定解,长度 15 km及以上的基线在双差固定解和双差浮点解中选择最优结果。对解算结果不好的基线作单独解算,通过删减卫星、删减时隙和改变卫星高度角等方法改善基线解算结果。
(2)三维无约束平差
经过选择,共计选择353条观测质量较好的基线组成基线网进行平差。三维无约束平差前,进行重复基线和独立闭合环的计算检核。根据CoasGPS软件按最小环路原则搜索,353条基线共计组成193个独立闭合环,85条重复基线。经统计所有独立环各坐标分量及全长闭合差均满足规范要求,所有重复基线长度较差满足规范要求。独立闭合环最大闭合差,重复基线最大较差统计如表3、表4所示。

表3 独立闭合环最大闭合差

表4 重复基线最大较差
基线向量改正值绝对值、最弱点点位中误差、最弱边角精度是衡量三维无约束平差精度的重要指标。经统计最弱点G852点位中误差 4.5 mm,最弱边G850-G851相对精度1/401321,基线向量改正值绝对值均小于2σ。综合以上指标,复测基线的解算和三维无约束平差成果满足规范要求。
(3)二维约束平差
根据控制网特点,MZ、XSQ、QSH32、G824、G833、G852、G857作为拟稳控制点为起算点进行二维约束平差计算,选择点位均匀分布于控制网中,有利于提高网形强度和精度的均匀性。
作为二维约束平差的起算点要求有良好的内符合精度,否则会使GNSS控制网产生扭曲变形。起算点包含误差是绝对的,关键是误差的相对大小是否在合理范围内,因为需要对起算点进行必要的稳定性检核[5]。
起算点稳定性检验的核心思想就是判定起算点的内符合精度是否满足GNSS控制网平差要求,通过比较二维约束平差后整个控制网精度相较于三维无约束平差后整个控制网的精度是否明显降低,来判断起算点是否给约束平差带入粗差。首先,比较两次平差后精度特征量(表5),改正数加权平方和PVV、最弱点点位中误差和最弱边精度;然后,比较控制点相关同名基线两次平差改正数之差(表6),看是否大于2σ(σ计算见式(1)),若大于说明该控制点的稳定性存疑,应剔除,然后换其他点位进行约束平差,若还是大于,则应继续剔除后换点,直至较差小于2σ。

表5 精度特征值对比

表6 同名基线改正数最大较差
经比较分析,二维约束平差后控制网精度特征值中PVV增大,最弱边精度降低但仍远高于规范1/100000的要求,最弱点精度没有降低。同名基线向量改正数最大较差小于2σ。综合判断,选择的控制点稳定性满足要求,复测精度满足规范要求。
4 控制点稳定性分析
4.1 单限差指标
根据《城市轨道交通工程测量规范》要求,同一控制点的复测与原测成果坐标分量较差的极限误差应小于 2 m(m为复测控制点的点位中误差)。
复测后,坐标分量较差大于2 m共计21点(见表7),且较差分布均匀,没有明显规律,也说明复测起算控制点选择合适,复测较差并不是完全由起算控制点导致。《城市轨道交通工程测量规范》在复测精度满足要求的基础上,仅从坐标分量较差一个维度做出要求,有一定的局限性,导致成果更新比例过大,根据城市轨道交通盾构掘进多的特点,引入距离较差和方位角较差两个约束参数。

表7 复测与原测成果较差

续表7
4.2 距离较差指标
相邻控制点的复测距离和原测距离一定存在较差,如果控制点是稳定的,则较差主要是由测量误差引起。反之,如果较差明显大于测量误差,则说明至少一个控制点是不稳定的。
复测及原测相邻点间距较差为:
ds=S复-S原
(1)
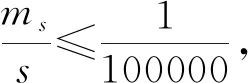
4.3 方位角较差指标
方位角主要为城市轨道交通工程区间施工提供掘进方向,如果方位角偏差较大则会影响地下导线的横向精度,严重的话到时区间无法正确贯通。《城市轨道交通工程测量规范》对复测成果的坐标方位角精度没有做具体要求,《高速铁路工程测量规范》中对卫星定位控制网基线边方向中误差有具体要求,根据此要求隋俭武等人[6]计算出方位角较差限差为4.8″,刘志等人[7]计算出方位角较差限差为3.64″。以上计算未考虑方位角偏差引起的贯通横向中误差,城市轨道交通工程通常是单项掘进,由一端控制点指导施工前进。方位角定向误差在贯通面上引起的横向中误差为[8]:
(2)
式中:mα—定向方位角中误差;S—始发边至贯通面距离;ρ—206265。
《城市轨道交通工程测量规范》规定地下隧道横向贯通中误差不应超过 ±50 mm,根据地下施工的实际情况,横向贯通误差主要由地面控制测量误差、竖井联系测量误差、地下控制测量误差三个主要方面构成,其中地面控制测量误差又可以分为起算点误差(主要是方位角误差)m方和地面趋近导线测量误差m测两个主要部分。各项误差影响相互独立,则:
(3)
式中:m1—地面控制测量引起的横向中误差;
m2—竖井联系测量引起的横向中误差;
m3—地下控制测量引起的横向中误差。
综合考虑现代测量技术及测量环境因素,采用不等精度分配原则,精度分配如下:
m1=1 m,m2=1 m,m3=2 m
则有:m=±20.41 mm

根据表7,在坐标分量较差超2 m的点位中,所有相邻控制点边长较差小于 10 mm,相对精度均高于1/100000,仅有一个方位角较差超2″,综上分析,本次复测仅对控制点G839坐标进行更新。
5 结 论
本文介绍了城市轨道交通工程GNSS控制网复测的详细过程,采用起算点相关同名基线比较法对起算控制点的稳定性进行检核,通过实际数据证明了该方法的可行性和复测精度的可靠性。
坐标分量较差法对于城市轨道交通工程GNSS控制网复测成果更新存在着较大的局限性,在此基础上加入距离较差、方位角较差组成三参数限差法对于判定控制网稳定性减少坐标更新比例效果明显。此外,部分学者还提出了夹角差指标,该指标本质上与方位角较差指标相同,本文未对此进行阐述。

