道路工程竖曲线测设精准计算模型

郭旭，徐万鹏

(1.深圳市勘察测绘院(集团)有限公司，广东 深圳 518028； 2.中铁十五局集团有限公司，上海 200070)

1 引 言

铁路、公路、轨道交通等道路工程的线路纵断面，是由许多不同坡度的坡段连接而成的。两相邻坡段的连接点，称为变坡点。车辆通过变坡点时，由于坡度方向发生突变，会产生附加的力和加速度，对车辆平稳运行和乘坐舒适性造成很大影响。为了缓解变坡点处坡度的急剧变化，使车辆平稳通过变坡点，应在相邻两坡段间设置竖曲线[1]。

在我国，竖曲线通常采用圆曲线或二次抛物线[1，2]。其原因如下：

如图1所示，标准抛物线的基本方程为[2]

图1 标准抛物线与圆曲线的几何关系

x2=2Py

若取抛物线参数P为竖曲线的半径r，则有：

(1)

另外，以点R(r，0)为圆心，半径为r的圆的方程为：

x2+(y-r)2=r2

即，对于圆曲线，有

(2)

设计道路纵断面时，由相邻坡段引起的转坡角ω非常小，对于切点A和切点B之间的竖曲线而言，y远小于x，所以，y2≪x2

于是，从式(2)中舍去更高阶无穷小y2，对y的影响可以忽略不计，因此，可得：

(3)

由式(1)和式(3)可知，竖曲线采用圆曲线或二次抛物线，几乎是等价的。

在式(1)和式(2)中，y坐标是计算竖曲线对应的道路设计高程的一个最重要的参数。很显然，对于计算y坐标而言，式(1)比式(2)要简单得多。因此，在电算不普及的手算年代，通常利用二次抛物线来计算竖曲线对应的线路高程，并一直沿用至今。由于二次抛物线的弦长计算复杂，在实际应用时，通常利用圆曲线计算竖曲线要素，利用抛物线计算竖曲线的设计高程。

2 传统竖曲线测设计算方法存在的问题

设前、后坡段的坡度为i1和i2。设置竖曲线时，如果i1i2，则称凸型竖曲线。道路工程勘测设计时，通常只提供每个变坡点对应的里程KE和高程HE，而竖曲线上各点对应的设计高程，需要通过竖曲线数学模型计算求得。现以凹型竖曲线为例，对传统竖曲线测设算法进行分析和研究，找出传统算法存在的问题。

如图2所示，如果前、后坡度大小相等，符号相反，则变坡点E将位于y轴上。除此而外，变坡点会偏离y轴一定距离t。为精确计算竖曲线头、尾，即垂足A和B的里程和高程，从理论上讲，首先应求得竖曲线对应的切线长AE和BE，然后利用变坡点里程KE，减去切线AE的平面投影长度，可以得到竖曲线起点A的精确里程KA，即：

图2 竖曲线传统算法示意图

KA=KE-AE·cos(tan-1i1)

进而可求得A点的精确高程

HA=HE+i1(KA-KE)

同理，可以得到竖曲线终点B的精确里程和高程，即

KB=KE+BE·cos(tan-1i2)

和

HB=HE+i2(KB-KE)

实际计算时，二次抛物线对应的切线长T很难精确求得，通常是利用圆曲线对应的参数，近似代替二次抛物线对应的参数[4～6]。具体算法如下：

(1)利用转坡角和圆曲线的半径，近似求得竖曲线的近似长度，即：

L=rω≈r(tan-1i1-tan-1i2)

由于i1和i2都很小，近似可得：

L≈r(i1-i2)

(2)假定t=0，可得竖曲线切线长的近似值：

之所以假定t=0，其原因如下：

如图1，假定前、后坡段不以y轴左右对称，则前、后坡道引起的转坡角的绝对值不相等，设其差值为dω，则有：

dω≈|i1|-|i2|

于是，可得圆曲线的圆心偏离y轴的水平距离为：

dR≈r·dω

假定变坡点对应的圆曲线的正矢为e，则有：

对于实际道路，正矢e非常小，通常在厘米至分米的量级上，dω更小，通常小于0.01，因此，假定t=0，几乎不影响运算结果。

(3)切线上任意点与竖曲线之间的竖距

即

由于

所以

(4)

式(4)中，l为竖曲线上任一点至竖曲线起点(或终点)的距离，r为竖曲线的半径。

(4)当l=T时，由式(4)可求得竖曲线的外距：

由以上推导可知，竖曲线计算的最终目的是确定道路设计纵坡上指定桩号的设计高程。即，求得竖曲线上任一点的切线高程

HQ≈HE±i(T-l)

及其改正值

进而求得该点的设计高程。对于凹型竖曲线，其设计高程为：

Ha≈HQ+h

对于凸型竖曲线，其设计高程为：

Ht≈HQ-h

经过以上分析，可知竖曲线测设的传统算法主要存在以下问题：一是数学模型不严密，用在教科书上，不利于学生理解；二是近似计算，舍入误差较大；三是计算过程烦琐，容易出错；四是需要大量的判断，不利于电脑编程运算。

目前，编程计算器和电脑已经非常普及，加之交通运输的速度不断提高，特别是高速铁路的普及，竖曲线的测设精度通常要达到毫米至亚毫米级，计算精度要求更高，采用传统近似算法，已远远无法满足高精度测量和计算的需要，规范和教科书也亟待更新。诸如文献[3]等大量的文献，也都对上述问题进行过很多研究和论述，并提供了一些精确算法，遗憾的是：这些文献只注重了计算精度，没能找出简单实用的计算公式。

3 精准竖曲线测设计算统一模型

3.1 精确确定竖曲线的桩号范围

如图3和图4所示，无论是凹型竖曲线，还是凸型竖曲线，由于前、后纵坡线和竖曲线在同一个铅锤面内，圆曲线的圆心O也在该铅锤面内，且凹型竖曲线的圆心位于道路中心线的正上方，凸型竖曲线的圆心位于道路中心线的正下方。由图3可知，前、后坡段引起的转坡角分别为：

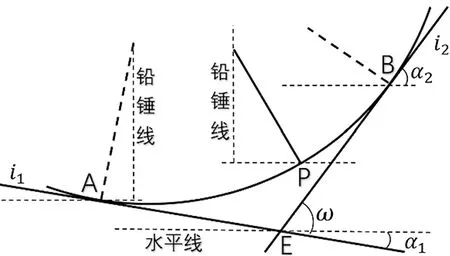
图3 凹型竖曲线计算示意图

α1=tan-1i1

(5)

和

α2=tan-1i2

(6)

上坡为仰角，转坡角为正，下坡为俯角，转坡角为负。

前、后坡段引起的总的转坡脚为：

ω=α1-α2

(7)

由图1可知，竖曲线对应的圆心角为|ω|。设圆曲线半径为r，则可求得竖曲线对应的切线长T为：

(8)

利用切线长和前、后坡段引起的转坡角，可求得竖曲线起点A和终点B的精确桩号，以及A和B的精确高程分别为：

KA=KE-Tcos(a1)

(9)

KB=KE+Tcos(a2)

(10)

HA=HE+i1(KA-KE)

(11)

HB=HE+i2(KB-KE)

(12)

因此，竖曲线精确的里程范围，即桩号范围，位于闭区间[KA，KB]上。

3.2 凹型竖曲线计算的精确模型

如图3所示，对于凹型竖曲线，其圆心O位于道路中心线的正上方，无论是上坡或下坡，利用竖曲线起点A或终点B，都能精确求得圆心O的高程，和其对应的桩号，即：

HO=HA+rcosα1=HB+rcosα2

(13)

和

KO=KA-rsinα1=KB-rsinα2

(14)

如图3，假定凹型竖曲线上任意一点P对应的里程，即桩号为KP∈[KA，KB]，可求得圆心O到P点的里程的差值，即桩号差值，为：

d=KP-KO

(15)

于是，利用圆心O的高程，可以精确求得P点的高程为：

(16)

式(13)、式(14)、式(15)、式(16)，即为计算凹型竖曲线的严密、精确模型。其中，式(15)的几何意义是：d的绝对值，就是竖曲线对应的圆心O，以及竖曲线上任意点P，在水平面上的投影点之间的距离。

3.3 凸型竖曲线计算的精确模型

如图4所示，对于凸型竖曲线，其圆心O位于道路中心线的正下方，无论是上坡或下坡，利用竖曲线起点A或终点B，也能精确求得圆心O的高程，和其对应的桩号。即，不仅式(15)有效，还有：

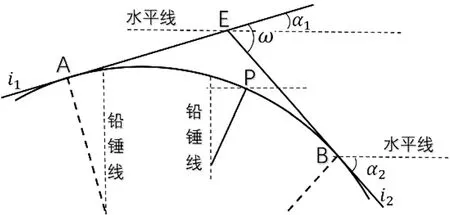
图4 凸型竖曲线计算示意图

HO=HA-rcosα1=HB-rcosα2

(17)

和

KO=KA+rsinα1=KB+rsinα2

(18)

因此，利用圆心O的高程，也可精确求得P点的高程为：

(19)

式(15)、式(17)、式(18)、式(19)，即为计算凸型竖曲线的严密、精确模型。

3.4竖曲线计算的统一模型

定义符号变量f

(20)

对于竖曲线，式(20)中的i1=i2实际上是不存在的，之所以列立出来，只是为了表达数学推理的严密性。

综合式(13)和式(17)，可得圆心O的高程：

HO=HA+f·r·cosα1=HB+f·r·cosα2

(21)

综合式(14)和式(18)，可得圆心O的里程：

KO=KA-f·r·sinα1=KB-f·r·sinα2

(22)

综合式(16)和式(19)，可得：

(23)

将式(5)和式(22)代入式(15)，可得：

d=KP-KA+f·r·sin(tan-1i1)

(24)

将式(5)和式(21)代入式(23)，可得：

(25)

式(24)和式(25)，即为计算竖曲线的严密、精确的数学模型。

式中：KA、HA为竖曲线起点A对应的里程和高程；

f为符号变量，凹曲线取1，凸曲线取-1；

r为竖曲线的半径；

i1为竖曲线起点A所在坡道的坡度；

KP为竖曲线上任意一点P对应的里程，即桩号。

4 工程应用与模型评价

本文导出的竖曲线计算模型，基于严密推理，不存在舍入误差，因而，计算是精准的。该模型于2010年首先应用于上海力信研制的盾构导向系统中。该导向系统在国内的市场份额一度超出50%，在北京、上海、广州、深圳等众多城市地铁工程中大量采用，效果良好。不仅如此，该模型易于理解，公式简单，规律性强，适合计算机编程运算，已被多家软件公司采用。京沪高铁建设期间，多期高级测量工培训班讲解该模型，学员普遍反映该模型规律性强，易于理解。下面是笔者基于C语言编写的竖曲线计算的程序片段。

{

int f=(i1

double d=Kp-Ka-f*r*sinl(atanl(i1)))；

return Ha+f*(r*cosl(atanl(i1))-sqrtl(r*r-d*d))；

}

可以看出，短短3行代码，就能解决复杂问题，且得到的计算结果不存在模型误差，而采用传统算法，通常需要上百行代码才能解决同样的问题。