数学“史学形态”向“教育形态”的转化*

冷 悦 陈惠汝 孔维娜

（黄冈师范学院 湖北黄冈 438000）

引言

函数概念是各个教育阶段重要的知识点之一，是常量数学向变量数学转变的开始，函数思想贯穿整个高中教材的内容，是连接初等数学与高等数学的纽带。理解函数的基本概念及其表现出的函数基本思想，是整个高中阶段每一位学生都应掌握的技能之一[1]。

纵观数学相关知识的发展史可知，函数的概念从无到有，从零散到完善，经历了300多年漫长而曲折的过程。随着时代的不断发展，函数的概念不断优化并为人们所认可，学习的范围也越来越广，融合的知识点越来越多。但在现如今函数的概念教学过程中，初中与高中关于函数基本概念的界定仍然存在着差异：初中通过学习函数之间的变量关系得到函数解析式。高中阶段，函数概念的改变引起了学生的认知冲突。学生在原来已有的知识经验的影响下，已形成思维定式。若教师此时直接讲授新的课程内容，会使学生理解困难，对函数概念知识点产生混淆。事实上，从初中到高中，学生们所学习的函数概念并不是简单知识的深化，而是与历史上函数概念的发展顺序相类似。历史上的函数概念的演变是来自多个方面：社会变迁、科学发展、人类进步……在教学中，有许多问题需要通过知识的发展过程来阐释。但在教学的过程中，教师因各种原因很少有机会能提到知识的发展，大部分教师都仅仅依据教材的内容来进行教学[2]。

《普通高中数学课程标准(2017版)》在教学建议中写道：“在教学活动中，教师应有意识地结合相应的教学内容，将数学文化渗透在日常教学中，引导学生了解数学的发展历程，有利于激发学生的数学学习兴趣，提升数学学科核心素养。”数学史作为数学文化的重要部分，它蕴含着丰富的教学素材，可以与教学内容相融合，尤其数学概念教学，不仅有助于学生更好地理解知识的本质特性，而且能够培养学生的数学核心素养。鉴于此，故分析基于数学史“函数的概念”教学案例，以引起教育硕士等未来教师的注意，更好地开展数学课堂教学，提高教育硕士培养质量[3]。

一、创设情境，复习引入

风和日丽的清晨，L教师迈着轻快的脚步走进了教室里，今天她要讲的是人教版高中数学必修一第三章内容函数的概念，她早早就做好了准备工作，查阅了相关的数学文化史，准备好了要用的教具等。

师：同学们，函数对于我们来说并不陌生，谁能告诉我，初中函数的定义是什么？

生：一般的，在某一个变化过程中如果有两个变量x和y，对每一个确定的x值，都有唯一确定的y值与之对应，我们就称y是x的函数，其中x称为自变量，y称为因变量。

师：同学们的表述非常正确，依据之前所学的定义，同学们能判断一下y=3是函数吗？

生：(学生一脸疑惑的摇摇头)

师：这就是我们高中还要继续学习函数的原因，因为初中函数的定义并不完善，事实上，函数概念的发展经历了300多年漫长的过程，同学们想知道历史上都有哪些数学家为此作出了了不起的贡献吗？

教师活动：教师接着通过PPT依次放映莱布尼兹、欧拉、狄利克雷、李善兰四位著名数学家的图片，并指出本节课将继续沿着四位数学家的脚步，再次探究函数的概念，从而引入所学章节《函数的概念》。

二、基于历史，探究新知

教师结合多媒体向学生讲解早期函数发展来源，并向学生说明早期函数的作用，进而基于历史，让学生了解函数发展的历史渊源，激发学生的学习兴趣。

探究1：引导学生从“解析式”说到“变量依赖关系”的转变。

教师活动：教师首先让学生阅读课本60页和61页的四个问题，教师和学生共同探究并依次解决这四个问题，通过问题1和问题2的探究，让学生清楚函数关系是可以用解析式来表达的，并由此向学生介绍函数“解析式”定义的由来，是早在1748年瑞士数学家通过不断探索后给出的，从而丰富学生的数学文化，加深学生对函数概念的认识；通过问题3中的空气质量指数变化图和问题4中的恩格尔系数表格的相关问题探究，让学生产生认知冲突，意识到函数的解析式定义已经不能够解释这类型的函数，从而引导学生要对函数的概念进行进一步的完善，最后实现从函数“解析式”定义向“变量依赖关系”定义的转变，同时向学生介绍相关的数学史，指出欧拉也发现了解析式定义的局限性，并在1755年重新定义了函数的概念，即函数的变量依赖关系定义，让学生体会以数学家的视角来探究函数的概念，更身临其境[4]。

【教学片段】

师：我们一起来看问题4。表1是我国某省城镇居民恩格尔系数变化情况，设年份为，恩格尔系数为。

表1 我国某省城镇居民恩格尔系数变化情况

师：请同学们观察，表中的数据是否能构成函数关系？

生：能，因为一个年份对应一个恩格尔系数。

师：那表中的数据能用函数解析式来表示吗？

生：不能用解析式表示。

师：也就是说，函数的解析式定义在这里已经不适用了，那我们怎样解决这个问题呢？

生：进一步完善函数的概念。

教师活动：教师肯定学生的说法，并向学生讲解著名数学家欧拉在当时也发现了解析式定义的不完善，并通过自己的不断研究和探索，重新定义了函数的概念，也就是函数的“变量依赖说”定义，接着ppt展示该定义。

探究2：引导学生从“变量依赖关系”到“变量对应关系”的转变

例2：常数函数y=2(x∈R)。

例3：某市的照相馆收费标准是，5张以内收费27.5元，超过5张，每张按2.5元收费，请你计算张数分别为4张、5张、6张、7张时，需要支付的费用元。

师：对于例2，请同学们思考，是否可以用变量依赖来定义函数呢？并说明原因。

生：不能。因为变量依赖关系是以存在两个变量为前提的，而常数函数y=2(x∈R)只存在一个变量，不符合该定义。

师：也就是说，变量依赖并不能定义常数函数。那我们接着看例3，请同学们分别计算出支付的费用，并思考能否用变量依赖关系来定义这个函数呢？

生：也不能。因为当x变化时，对应的y值并没有都发生改变。

教师活动：通过上述两个例子，告诉学生“变量依赖关系”刻画函数具有一定的局限性，且对于常数函数和两个变量之间不存在依赖关系的函数不适用，进而引导学生们还需继续完善函数的概念，使其适用范围更广[5]。

师：怎样完善该定义呢？

生：把“依赖”换成“对应”。“对应”包含的两个变量中，当一个变量变化时，另一个变量可以随之变化，也可以保持不变。

师：看来同学们对于“依赖”和“对应”已经理解很透彻了，那么我们如何对之前的定义进行修正呢？

师生活动：师生共同探讨并对函数的“变量依赖关系”定义进行修改，同时教师在黑板上板书函数的修改后的定义——“变量对应关系”定义，并指出该定义就是初中所学的函数的定义。

探究3：引导学生从“变量对应关系”到“集合对应关系”的转变。

教师通过ppt向学生展示狄利克雷函数：

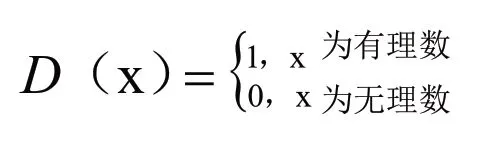
并根据该定义让学生思考，狄利克雷函数是否能用“变量对应关系”来解释，激发学生探究的欲望，有利于教学进一步开展。

生：对于狄利克雷函数，可以用“变量对应关系”来解释，也就是对于每一个x值，对应的值都是唯一的。

师：（教师肯定）请同学们思考，能否用更简洁的语言来表达狄利克雷函数吗？

生：可以用集合的相关知识来表达狄利克雷函数，把x的取值范围用集合表示出来，同理把x所对应的y的值也用集合表示出来。

师：这位同学的想法非常棒，那么集合中的元素有哪些呢？

生：集合中的元素分别有0和1。

师：看来集合语言的确可以使函数表示更简单。那么我们现在是否可以用集合和对应的语言对函数的定义进行重新改进呢？

教师活动：通过对于狄利克雷函数的探讨，引导学生从“变量对应关系”向“集合对应关系”的转变，最后师生共同探究总结出函数的“集合对应关系”定义，教师在黑板上板书该定义。

三、基于历史，辨析概念

通过函数的“集合对应关系”定义，对函数的概念进行深入剖析，包括强调f（x）所表示的含义，强调函数的三要素以及强调两个函数相等的重要条件。

师：根据定义，我们可以看到，出现了新符号f（x），请问同学们f（x）有什么含义呢？我们各个小组之间可以交流一下。

组1：f（x）表示f乘以x的值。

组2：y。

师：学生要理解这个知识似乎确实很难，大家可以考虑从函数的历史出发（PPT展示）。

函数一词最早是德国数学家莱布尼茨提出来的，函数的英文是function，表示“发挥作用”。而我国清代数学家李善兰将function翻译为中文“函数”，这就是我国函数一词的由来，并给出定义：“凡式中含天，为天之函数。凡此变数中函彼变数，则此为彼之函数。”其中“函”与“含”同义，“含”在此也有“起……作用”的意思。因此，f（）代表起一定作用的工具，当对应关系f作用到x值时，f（x）表示在值对应下的函数值。

生：（学生缓缓点头，表示理解）

师：那想一想f（a）和f（x）有没有联系？

生:f（x）是在任意x值对应下的函数值，f（a）是在x=a值对应下的函数值。

师:同学们似乎理解了f（x），f（x）是变量，而f（a）是常量，当自变量为a时，对师：函数概念中的三要素：定义域、对应关系、值域三者谁最重要呢？

生1：对应关系。

生2：定义域。

师：其实对应关系和定义域都是非常重要的，首先定义域和对应关系确定了，那么值域也就确定了，那请同学考虑一下这个问题，f(x)=3x+1、t(a)=3a+1表示同一个函数吗？

生：是的，因为定义域和对应关系都是一样的。

教师总结：也就是说，虽然函数常用f表示，但是也可以用其他字母（如h、t、g等）来表示，不同字母的表示不影响函数的本身，函数符号f（x）表示与x对应的函数值，不是f乘以x，而是一个数。如果函数的定义域和对应关系相同，则可以说这些函数是相等的。

生：（学生豁然开朗）

师：今天我们跟随数学家们的脚步，体会了函数概念的演变过程，希望同学们也能像数学家那样勇于探索、不懈努力，下一位作出如此贡献的数学家说不定就在我们同学之中。

结语

本节课是一所省示范高中的一堂有关于函数概念的数学课，本案例中的教师根据高中生对函数概念的理解与历史上的数学家的理解具有一定的相似性。开展了基于数学史的“函数的概念”的教学。在教学过程中，教师根据函数概念的历史演进过程，重构函数概念的发展历史，设置相应的问题，让学生亲身经历数学家“一次次提出概念、一次次推翻概念、一次次修正概念、一次次完善概念”的探究过程。这无疑告诉我们：数学史为扫清某些数学概念的教学和学习障碍开辟了一条新的思路。数学家是怎么发现问题、提出问题、分析并解决问题的，这是我们在课堂上应该深入探讨的，也是激发学生学习兴趣和探索欲望的“引子”，在课堂中这种思想和创造的过程是很有意义的。