考虑压裂液渗吸的压后压裂液返排的数值模拟

王继伟，曲占庆，郭天魁，陈铭，吕明锟

非常规油气开发教育部重点实验室，中国石油大学（华东）石油工程学院，山东青岛266580

水力压裂技术是老油田升级改造和低渗致密油藏开发的有效措施，压后压裂液返排作为一个关键环节关系着压裂效果和压后增产状况[1-3].一方面压后裂缝闭合前支撑剂悬浮于裂缝中，如果压裂停泵后立即大排量返排，会造成支撑剂大量回流，导致裂缝的导流能力大幅降低[4-6]；另一方面，如果返排速度过慢，压裂液大量滤失会造成储层二次伤害[7-8].但是，对于低渗透致密油气藏特别是页岩储层的水力压裂，压裂液渗吸的影响不可忽视.屈亚光等[9]指出，渗吸主要发生在关井阶段.杨海等[10]基于中国湖北威远地区龙马溪组36 口页岩气井压后返排数据分析压后关井对产量的影响，认为一定时间的关井有利于提升气井累积产气量.因此，为增强压裂施工效果，提高压后产能，需要研究考虑渗吸的压裂液返排制度优化方法.李小龙等[11]分析了压裂液的返排速度和破胶黏度对支撑剂总回流量的影响规律，确定了最佳返排流量为100 L/min，最佳返排时机为压裂液破胶黏度降至5 mPa·s时.韩慧芬等[12]通过对大量页岩气井返排数据分析，发现初期采用慢返排模式更有利于提高返排率和单井产能，提出了“油嘴进行控制、逐级放大、连续、平稳”的排液制度.但上述得到的压后返排制度均属于经验方法，无法得到返排过程中的压力排量数据，不能进行定量设计.张锋等[13]基于物质平衡原理，利用渗流力学和工程流体力学理论，建立了支撑剂回流及裂缝闭合时间计算模型，得到了不同时刻井口压力与最佳油嘴匹配关系图版.陈昱辛等[14]研究了多层段统一返排情形的返排计算方法，建立了多层段压后统一返排模型.但是目前关于压后压裂液返排制度优化的数值模型尚未考虑压裂液渗吸的影响.杜洋等[15-17]开展了渗吸实验，指出压裂液渗吸有利于改善储层物性，增加渗流通道，依靠渗吸驱油能够提高采收率.姚军等[18-19]基于渗吸采油机理和渗流理论，建立了渗吸采油计算模型，分析了压裂液渗吸对产能的影响.

本研究基于油水两相渗流原理和连续性原理建立考虑渗吸的压后返排数值模型，进行压后压裂液返排过程的数值模拟，结合支撑剂临界回流速度计算模型，形成一套压后压裂液返排工作制度优化设计方法，可用于指导现场压裂返排施工设计.

1 返排数值模型

1.1 井底压力计算模型

压裂停泵后，随着压裂液的滤失和返排，井底压力随之下降，同时裂缝张开体积随之减小.假设水力裂缝为双翼对称垂直缝，裂缝横截面为椭圆，裂缝闭合过程不受支撑剂影响.根据压后关井期间和返排阶段裂缝内的流体体积平衡原理，建立井底压力计算模型[20].

在压后关井期间，裂缝闭合过程中裂缝体积的变化量ΔV（f单位：m³）等于停泵后的压裂液的滤失量ΔV（l单位：m³），即

在压后返排期间，裂缝体积变化量等于压裂液滤失量和压裂液返排量ΔVfb（单位：m³）之和，即

1.1.1 考虑渗吸的压裂液滤失量计算

对于考虑渗吸现象的压裂液滤失过程，根据两相渗流理论，采用油水两相二维渗流模型描述，考虑油水微可压缩性，得到油水两相渗流微分方程、毛管压力方程和饱和度方程[21]分别为

外边界条件为

根据修正的Corey 方程，得到计算毛管力和相对渗透率的经验公式[22]，

其中，t为返排时间，单位：min；k为绝对渗透率，单位：μm2；kro为油相相对渗透率；krw为水相相对渗透率；ρo为油相密度，单位：kg/m3；kx和ky分别为x和y方向的绝对渗透率，单位：μm2；ρw为水相密度（返排液密度），单位：kg/m3；μo为油相黏度，单位：mPa·s；μw为水相黏度（压裂液黏度），单位：mPa·s；ϕ为孔隙度；So为油相饱和度；Sw为水相饱和度；po和pw分别为油相和水相压力，单位：MPa；Lx和Ly分别为储层模型的长度（x方向）和宽度（y方向），单位：m；Lf为裂缝长度，单位：m；p0为储层原始压力，单位：MPa；pf为井底压力，单位：MPa；Swc为初始含水饱和度；pc为毛管压力，单位：MPa；Sws为束缚水饱和度；Sor为残余油饱和度；为水相对渗透率曲线终点；a为水相对渗透率曲线的Corey 指数；为油相对渗透率曲线终点；b为油相对渗透率曲线的Corey指数；σ为油水界面张力，单位：mN/m.

考虑到裂缝及储层的对称性，为简化模型和减小计算量，选择1/4 储层作为研究对象，并进行不均匀网格划分，使靠近裂缝和井筒的网格较密集，远离裂缝和井筒的网格较疏松（图1）.求解式（3）至式（9）偏微分方程组，采用隐压显饱法（implicit pressure explicit saturation method，IMPES），即隐式求解压力，显式求解饱和度，经过差商变换，整理得到关于压力的离散方程，

图1 压裂液滤失模型网格划分示意图Fig.1 Schematic diagram of grid division of fracturing fluid loss model.

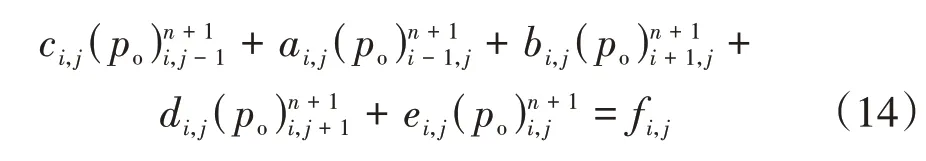
其中，系数项是与储层物性及网格划分相关的常数；ai，j、bi，j、ci，j、di，j和ei，j均为与储层物性及网格划分相关的压力扩散系数；fi，j为上一时步节点压力和边界条件的合成项.

求解式（14）得到po，根据毛管力方程得到pw，然后计算下一时间步的含水饱和度，接着继续求解下一时间步的压力.值得注意的是，计算过程中毛管力是根据上一时间步的含水饱和得到，并认为在Δt时间内保持不变.

根据达西渗流定律可得到压裂液滤失速度方程，以靠近裂缝的一层离散压力网格计算出离散化压裂液滤失速度，得到通过单个网格的滤失流量qi为

其中，下标i表示x方向网格序号；h为压裂液滤失高度，单位：m；Lx，i为裂缝x方向网格的长度，单位：m；pi，1为y方向第1 行第i个节点的压力，单位：MPa；μ为压裂液的黏度，单位：mPa·s.tn时刻的压裂液滤失总体积为

其中，pf为井底压力，单位：MPa；Δy1为y方向第1 排的长度，单位：m；Δt为时间步长，单位：s；m为x方向网格数.

1.1.2 压裂液返排量计算

打开油嘴进行压裂液返排，根据过油嘴的伯努利方程及连续性方程推导出不同时刻过油嘴后的返排流速[24]为

根据返排流速及油嘴或井筒半径即可得到不同时刻的返排流量，然后对时间进行积分得到压裂液返排体积，采用复合梯形公式将积分式进行离散，计算返排过程中不同时刻的压裂液累积返排量.

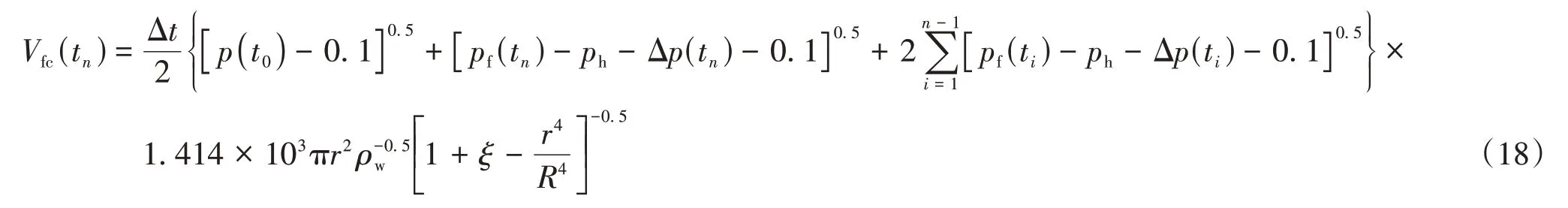
其中，ξ为嘴损系数；t0为压裂液返排的初始时间，单位：min；r为油嘴半径，单位：m；R为井筒半径，单位：m；p(t)为返排过程中t时刻的井口压力，单位：MPa；ph为井筒中液柱压力，单位：MPa；Δp(t)为返排过程中t时刻的沿程摩阻，单位：MPa.

井口压力可由井底压力减去垂直井筒液柱压力和沿程摩阻得到，其中，沿程摩阻Δp为

其中，ρl为井筒液柱密度，单位：kg/m3；λ为摩阻系数；L为井筒长度，单位：m；vl为井筒液体流速，单位：m/s.

1.1.3 裂缝体积变化量计算方法

根据PALMER 等[23-24]提出的拟三维裂缝模型，考虑应力差异，裂缝截面近似为椭圆形，椭圆的短轴即裂缝的最大缝宽.压裂停泵时裂缝宽度最大，随着压裂液的滤失和返排，缝宽逐渐减小.在裂缝闭合过程中，不考虑缝高和缝长变化，裂缝体积减小量只与裂缝宽度的减小相关，根据缝宽公式可推导出裂缝闭合过程中某时刻t裂缝体积减少量ΔVl(t)的计算公式[20]为

其中，Wmax(t)为t时刻裂缝的最大宽度，单位：m；γ为无因次泊松比；E为杨氏模量，单位：MPa；Hw为裂缝高度，单位：m；s1为储层最小水平应力，单位：MPa；Hp为储层厚度，单位：m；Lp为停泵时刻缝长，单位：m；ps为压裂停泵瞬间井口压力，单位：MPa.

1.2 支撑剂临界回流速度计算模型

在压裂液返排的过程中，支撑剂受压裂液作用发生运动，如果压裂液返排速度过快，则会造成支撑剂大量回流，使支撑剂发生回流的压裂液最小流速为支撑剂临界回流速度.本研究假设支撑剂颗粒为球形，支撑剂回流时受到的力有拖曳力、举升力、重力、液桥力、下压力和闭合应力，通过对这些力进行力矩平衡分析，推导出支撑剂临界回流速度公式.

在裂缝闭合前，液桥力可以忽略，下压力被考虑，闭合应力不直接作用于支撑剂颗粒，可推导出不同雷诺数Re下的支撑剂临界回流速度vc计算公式[4].

当Re≤2时，

其中，β=Cl/Cd=0.25，Cl为举升力系数，Cd为阻力系数；α为作用在支撑剂上的闭合应力方向；ds为支撑剂的直径，单位：m；ρs为支撑剂密度，单位：kg/m3；δ为液膜系数，δ=2.13 × 10-7；hs为支撑剂距裂缝顶端的距离，单位：m.

当裂缝闭合后，裂缝内的支撑剂受力发生改变，液桥力存在而下压力可以忽略，裂缝闭合应力将会直接作用于支撑剂颗粒.通过对支撑剂受力进行力矩平衡分析，得到不同雷诺数下的支撑剂临界回流速度[4].

当Re≤2时，

2 模型求解与验证

2.1 模型求解

由式（13）、式（15）和式（18）可见，压裂液滤失量、返排量和裂缝体积减少量都是井底压力的函数，通过对每一时间步里的压力项进行迭代可得到该时刻准确的井底压力，进而计算出返排流量、压裂液滤失量及毛管力等参数.在返排阶段，油嘴选择满足最小化支撑剂回流和快速返排的原则，通过井底压力模型与支撑剂回流模型耦合计算，实现放喷油嘴的自动优选.计算过程通过MATLAB编程实现（图2），具体计算步骤如下：

图2 模型求解流程图Fig.2 Flow chart of model solving.

1）以停泵时的井口压力为初始值，加上井筒中液柱压力可以得到井底压力，设置一个时间步长，并假设下一时刻井底压力为

3）选取一个合适的油嘴直径（对于关井阶段，忽略此步骤），根据计算当前时间步长内的压裂返排量；

5）根据体积平衡公式（1）和公式（2），采用牛顿-拉夫森方法进行迭代，得到满足精度要求的下一时刻井底压力；

6）根据井底压力计算返排量、滤失量和毛管力，判断裂缝是否闭合，计算支撑剂临界回流速度；

7）重复步骤2）至步骤6）过程，直到给定时间结束.

2.2 模型验证

以大庆油田LX3 井为例，对该模型进行验证.LX3 井为直井，分两段进行了水力压裂，第1 段深度为3 514 m，第2 段深度为3 234 m，在两段压裂完成后统一进行压裂液返排.整理该井返排过程中监测的返排流量和井口压力数据，将该井返排实施的油嘴使用设置（表1）代入本研究返排数值模型计算返排流量和井口压力，该井返排模型关键参数如表2.

表1 LX3井返排油嘴设置Table 1 Settings of flowback nozzle of LX3 well

表2 LX3井返排数值模型关键参数Table 2 Parameters of the flowback model of LX3 well

将数值模拟结果与现场监测结果进行对比，如图3和图4.由图3可见，数值模拟的返排流量与实际监测的流量随时间变化趋势是一致的，早期的现场监测返排流量比数值模拟的更大一些，中期两者曲线基本重合，而后期误差相对较大，总体平均误差为13.8%.由图4可见，数值计算得出的井口压力与实际监测的井口压力数据整体变化趋势一致，两条曲线之间的平均误差为15.5%.从数值模拟结果与现场监测结果的对比来看，整体误差小于20%，在工程应用领域本返排数值模型更加相当准确，可以用来指导现场压裂返排施工设计.

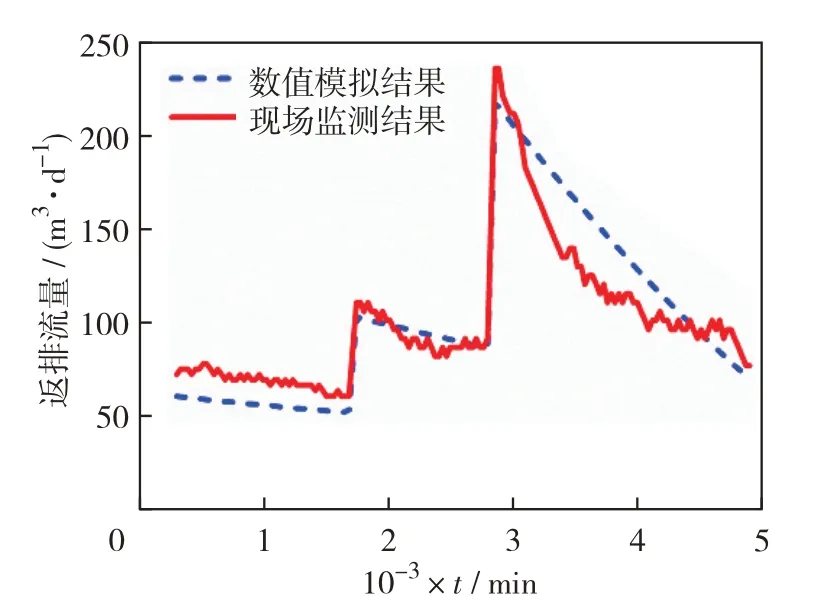
图3 LX3井返排流量对比曲线Fig.3 Comparison curves of flowback flowrate in LX3 well.Red solid line is the flowrate as function of time for actual testing result and the blue dashed line is the numerical result.

图4 LX3井井口压力对比曲线Fig.4 Comparison curves of wellhead pressure in LX3 well.Red solid line is the pressure as function of time for actual testing result and the blue dashed line is the numerical result.

3 应用与分析

3.1 M87井返排制度优化设计

根据现场资料及小型压裂测试结果，收集整理长庆油田M87 井关键参数如表3，该井属于特低渗砂岩油井.应用本研究压裂液返排数值模型对M87井进行返排工作制度优化设计，结果如表4.在返排阶段的早期，由于裂缝未闭合，支撑剂容易回流，选择较小油嘴进行放喷；当裂缝闭合后，支撑剂不易回流，即可选择较大油嘴进行放喷.返排过程中压力和排量变化曲线如图5.

表3 M87井返排模型主要参数Table 3 Main parameters of the flowback model of M87 well

表4 M87井压裂液返排工作制度表Table 4 Fracturing fluid flowback working system of M87 well

由图5可见，在小油嘴放喷时井底和井口压力降低速度较慢，更换大油嘴后压力降低速度明显增大，在整个返排过程中，返排流量始终小于支撑剂临界回流流量.

图5 M87井返排过程中井底压力和排量变化曲线Fig.5 Pressure and flow rate curve during the flowback process of M87 well.Square black solid line is the bottom hole pressure as function of time(left axis),square red solid line is the flowback flow rate as function of time(right axis)and red solid line is the critical flow rate as function of time(right axis).

3.2 压裂液返排影响分析

在压裂液返排过程中，随着压裂液向地层的滤失，地层压力会增加，不同时刻的储层压力分布情况如图6.由图6 可见，储层大部分区域压力保持不变，仅在裂缝附近区域存在压力波动，且随时间的增加压力波动区域也随之增大；在返排结束时裂缝周围储层压力不会恢复到储层原始压力大小，而是增大了一些，这正是低压储层中压裂液渗吸滤失增能的体现.随着压裂液的返排和滤失，裂缝内压力逐渐降低，同时由于压裂液的滤失裂缝周围的地层压力会升高.在返排早期裂缝内压力大于裂缝外压力，而在后期裂缝内压力开始小于裂缝外部压力，此时地层流体开始向裂缝内渗流.从图7也可以看出，返排过程中的压裂液累积滤失体积曲线有一个顶点，说明在此之前压裂液从裂缝向地层滤失，而在此之后地层流体向裂缝中渗流.

图6 M87井在不同返排时间（a）10 min、（b）190 min、（c）300 min、（d）520 min、（e）1 000 min和（f）1 660 min时的储层压力分布Fig.6 Reservoir pressure distributions during flowback time of(a)10 min,(b)190 min,(c)300 min,(d)520 min,(e)1 000 min,and(f)1 660 min of M87 well.

图7 M87井压裂液累积滤失量和累积返排量曲线Fig.7 Cumulative filtration loss curve（circle red solid line）and cumulative flowback curve（square blue solid line）of fracturing fluid in M87 well.

地层产出液中含有原油，其黏度比压裂液要大，造成返排液体的黏度改变，需要明确不同产出液黏度对返排有何影响.另外，对于低压储层现场实施了一系列地层增能措施，地层压力也会发生很大波动.因此，以M87井为例，设置不同的地层产出液黏度和初始地层压力，进行数值模拟计算，分析其对压裂液返排的影响.

图8为压裂液返排量、滤失量及地层产出液量与地层产出液黏度的关系曲线，随着地层产出液黏度的增大，压裂液返排量会有所减小，但整体减小幅度较小.地层产出液量随黏度的增大而减小，在黏度小于100 mPa·s 时，地层产出液量减小幅度较大，而在黏度大于100 mPa·s 时，地层产出液量随黏度的增加基本保持不变.总体来说地层产出液量相对返排量和滤失量非常小，这主要是由于返排在自喷条件下进行，当井底缝内压力较低小于储层压力时，压裂液依靠自喷返排很快就要结束.分析不同产出液黏度下的返排流量和井底压力变化曲线，见图9.由图9 可见，在早期地层未出液时，不同产出液黏度下的返排流量和井底压力变化曲线均是重合的；而在地层出液后，产出液黏度越大压裂液排量越小，井底压力则越大，这是由于产出液黏度较大造成井筒流动阻力增大，使得返排流量减小，且产出液黏度越大，这种阻力就越大.整体来看，在自喷条件下，由于产出液量很小，产出液黏度大小对返排影响甚微.

图8 不同产出液黏度下的压裂液返排量、滤失量及地层产出液量曲线Fig.8 Fracturing fluid flowback volume（circle black solid line，left axis），filtration volume（rhombus black solid line，left axis）and formation produced fluid volume（triangle red solid line，right axis）under different produced fluid viscosities.

图9 不同产出液黏度下的（a）井底压力及（b）返排流量变化曲线Fig.9 (a)Bottom hole pressure and(b)flowback flow rate as function of time under different produced fluid viscosities.

图10 为压裂液返排量、滤失量及地层产出液量与地层压力的关系.由图10 可见，随着初始地层压力的增大，压裂返排量明显增大，压裂液滤失量明显减小，地层产出液量也在增大，且初始地层压力越大地层产出液量增加越显著.分析不同初始地层压力下的返排流量和井底压力变化规律（图11）.由图11可见，不同初始地层压力下的返排流量变化趋势基本一致，其峰值随着初始地层压力的增大向后推移.特别地，当初始地层压力为26 MPa时，返排流量曲线中缺少了一个峰值，这是由于未满足更换油嘴规则，直到后期才更换了大油嘴，也造成了返排完成时间大幅增加.另外，随着地层压力的增大，井底压力降曲线变得更平缓，这是由于地层压力越大压裂液向地层滤失的量越小，使得井底压力降低速度变缓.

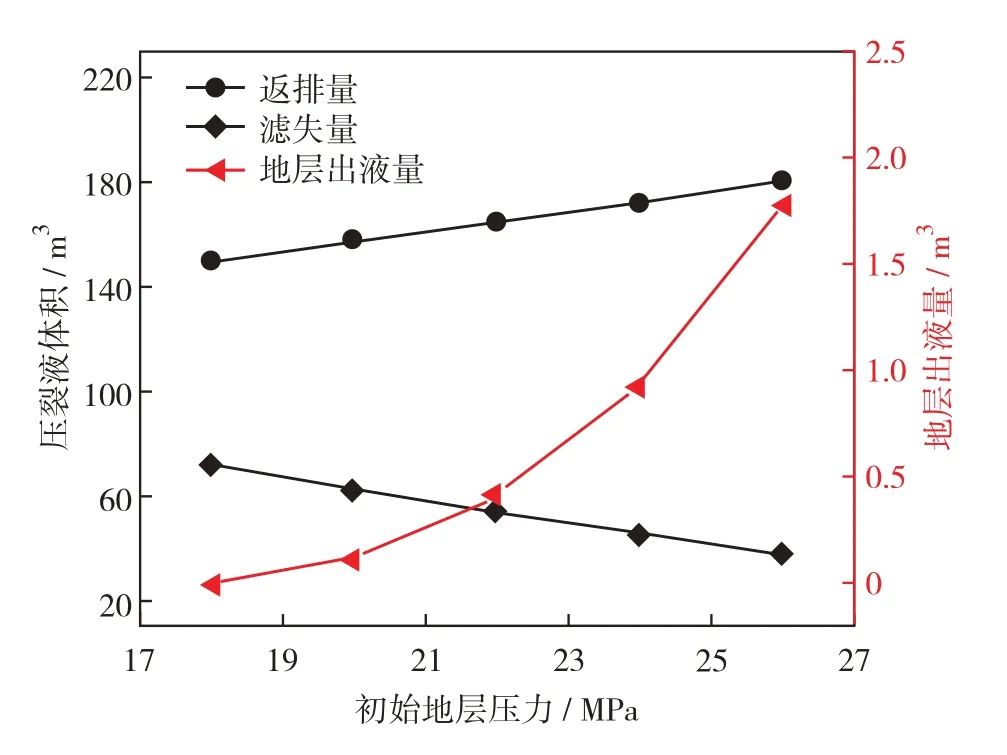
图10 不同初始地层压力下的压裂液返排量、滤失量及地层产出液量Fig.10 Fracturing fluid flowback volume(circle black solid line,left axis),filtration volume(rhombus black solid line,left axis)and formation produced fluid volume(triangle red solid line,right axis)under different initial formation pressures.

图11 不同初始地层压力下的（a）井底压力及（b）返排流量变化曲线Fig.11 (a)Bottom hole pressure and(b)flowback flow rate as function of time under different initial formation pressures.

结语

构建了考虑压裂液渗吸的压后返排数值模型，基于快速返排和控制支撑剂回流的原则形成了一套返排工作制度优化设计方法，实现了现场压裂返排施工时放喷油嘴的自动优化设计.压裂液返排后期会出现地层流体向裂缝渗流现象，在自喷返排情况下地层产出液量相对较小，对返排影响甚微；初始地层压力对压后压裂液返排影响比较显著，地层压力越大，井底返排压力降低越缓慢，返排时间越长.应用本研究返排数值模型模拟了大庆油田LX3井的压后返排过程，模拟的井口压力和返排流量与现场监测数据的平均误差分别为15.5%和13.8%，因此，该模型在现场应用方面具有较高的准确性.