考虑硬件损耗的智能反射面辅助无线携能通信系统

何春龙，王新龙，李兴泉，钱恭斌

1）深圳大学广东省智能信息处理重点实验室，广东深圳 518060；2）东南大学国家移动通信研究实验室，江苏南京 211189；3）深圳信息职业技术学院微电子学院，广东深圳518172

近年来，随着互联网技术迅速发展，通信需求和物联网（internet of things，IoT）设备数量也呈几何倍数增加[1].迄今大概已有百亿级甚至千亿级IoT设备接入无线网络，因此，急需要一个可扩展的无线设备解决方案，为未来无线网络提供无处不在的通信连接和能源供应[2].同步无线信息和能量传输（simultaneous wireless information and power transfer，SWIPT，亦称携能通信）系统模型能够在不影响传统系统模型中信息传输的情况下，同时给IoT 设备进行无线供能.ZHANG 等[3]研究了单用户多输入多输出（multiple-input multiple-output，MIMO）系统中用户所获得的信息速率和能量之间的权衡.然而，能量收集器的接收功率通常要比信息接收者的高得多，这是因为它们在实践中的应用要求有很大不同[4].

智能反射面（intelligent reflecting surface，IRS）作为第6代无线通信的关键技术，可用来提高无线通信频谱和能量效率[5-7].将IRS应用到SWIPT系统中，可解决能量收集器长距离传输效率低的问题.WU 等[2]研究了IRS 辅助的SWIPT 模型，通过部署IRS 来辅助基站到多个单天线信息用户和能量用户的信息/功率传输.WU等[8]研究了加权和功率最大化问题，证明IRS辅助的SWIPT系统不需要专用的载能信号.ZHOU 等[9]在SWIPT 系统中加入多个窃听者，提出一个平均保密率最大化问题.JIN 等[10]证明了全双工用户可以将接收到的能量转换成人工噪声以提高系统保密率.GONG 等[11]研究了IoT 网络中IRS 辅 助MIMO 的SWIPT 系统，考虑了IRS 处离散相移对信息接收端信噪比的影响，并提出最优分支定界算法和次优交替优化算法.在IRS辅助的通信系统中获取信道状态信息是比较困难的.ZHOU 等[12-15]使用了如信道估计和鲁棒性传输设计的方案来解决此问题.ZHOU等[12]研究了部分信道状态信息非完美和全部信道状态信息非完美对系统发射功率的影响，分别使用了有界误差模型和统计误差模型来解决通过S过程和Bernstein 型不等式重新表述的问题.ZHU等[13]在考虑了部分信道状态信息非完美情况下，研究了非线性能量收集模型下IRS 辅助SWIPT 的太赫兹安全系统，使用半定松弛SDR 来优化相移矩阵.ZHENG 等[14]为双IRS 辅助MIMO 通信系统提出一种新的高效信道估计方案，以解决其单反射链路和双反射链路的级联信道状态信息.有学者将机器学习和深度学习算法应用到IRS 通信模型，很大程度上提升了通信系统的性能.TAHA等[16]在SWIPT系统中使用深度强化学习算法解决了用户能量收集最大化问题.ELSAYED等[17]提出一种在最小波束训练开销的情况下预测IRS反射矩阵的强化学习框架.

以上研究都是基于完美硬件条件进行，未考虑硬件损耗相关问题，然而在实际通信系统中，收发器硬件总会存在一些不可避免的损耗[18-19]，影响源发射波束成形和IRS反射波束成形的失真，降低系统性能.残余收发器硬件损耗引起的失真噪声可建模为附加高斯分布，与信号功率成比例[20].BOULOGEORGOS 等[21]推导出IRS 辅助系统中断概率的封闭表达式，证明硬件损耗对频谱效率有显著影响的事实.SHEN 等[22]研究了最大化接收信噪比问题，同时考虑了硬件损耗的影响，结果表明与传统的信噪比最大化方案相比，该波束形成的设计对硬件损耗具有更强的鲁棒性.ZHOU等[23]研究了硬件损耗影响下IRS辅助安全通信系统的鲁棒传输设计，并对最大化系统保密率进行了分析.SAEIDI等[24]对多个IRS 辅助的全双工通信系统进行了研究，考虑每个节点的硬件损耗情况下，最大化系统的加权和速率.

本研究旨在分析考虑硬件损耗的IRS 辅助SWIPT通信系统的鲁棒性传输设计，主要贡献有以下2点：

1）在SWIPT 系统中考虑基站、信息接收者和能量收集器的实际硬件损耗，通过鲁棒性传输设计最大化所有信息接收者加权和速率.通过仿真实验证实了信息接收端的硬件损耗要比基站发射端的硬件损耗对系统的影响更大.

2）在能量收集、基站发射功率和IRS 相移的单位模约束下，本研究联合系统的基站预编码矩阵和IRS的相移矩阵，制定了所有信息接收者加权和速率最大化问题.

1 系统模型和问题的提出

1.1 系统模型

本研究提出的考虑硬件损耗的IRS 辅助MIMO的SWIPT系统如图1.假设共有KI个信息接收用户和KE个能量收集器，基站端的发射天线数量Nb＞1，信息接收用户和能量收集器的天线数量分别为NI＞1和NE＞1，信息接收者与能量收集器的集合为KI和KE，并在能量收集器附近部署M个IRS，用于扩展能量收集器的作用范围，或者增强远处信息接收者的信号强度.

图1 IRS辅助的SWIPT通信系统Fig.1 IRS aided SWIPT communication system.

假设每个信息接收用户接收到的数据流总量为d，满足1 ≤d≤min(Nb，NE），基站的发射信号为

其中，nI，k是第k个信息接收用户处的加性白高斯噪声，服从的正态分布，为噪声功率，INI为NI阶的单位矩阵.定义第k个信息接收用户接收到的无噪声干扰的信号矩阵为hr，kΦhb，r)s+nI，k.其中，mi为信息接收用户i处因硬件损耗产生的失真噪声，服从分布，μi为信息接收用户处的硬件损耗系数[23].同理，第l个能量收集器的接收信号为

第k个信息接收用户的可实现数据传输速率为

其中，Jk是第k个用户的干扰加噪声的协方差矩阵，

本研究采用一种线性模型[25]作为能量接收模型，通过忽略能量收集器处的噪声干扰，使能量收集器的总收集功率与总接收功率成比例.将基站发射给第l个能量收集器的级联信道定义为Zl=zb，l+zr，lΦhb，r.第l个能量收集器总收集功率为

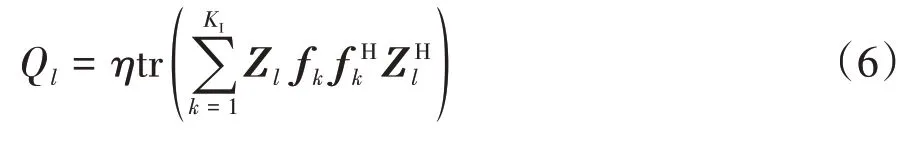
其中，η为能量转换效率，且0 ＜η＜1.本研究考虑能量收集器的最小能量约束，即

其中，αl为第l个能量收集器的能量加权因子，αl越大第l个能量收集器的优先级越高；Zˉ=为最小能量收集阈值.

1.2 问题的提出

本研究在基站最大发射功率、能量收集器最小收集能量以及IRS的单位模约束下，对基站的预编码矩阵f和IRS 的相移矩阵Φ联合优化，最大化信息接收用户的加权和速率（weighted sum rate，WSR），即

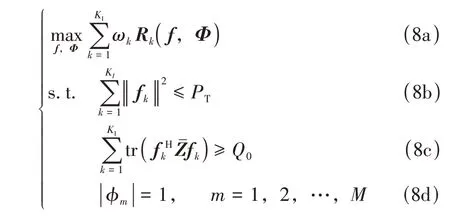
2 算法设计

由于问题（8）中优化变量高度耦合，本研究通过将式（8）转换成一种等价可行的问题，使优化变量解耦，再通过块坐标下降（block coordinate descent，BCD）算法来求解得出原问题的最优解.

2.1 原问题转换

为将原问题中高度耦合地优化变量解耦，采用最小均方误差的方法来简化原问题[26].引入信息接收用户端的解码矩阵U={Uk，∀k∈KI}，则每个信息接收用户的接收信号矩阵为

其中，Uk为第k个信息接收用户的解码矩阵，第k个信息接收用户的均方误差矩阵为

引入辅助矩阵W={Wk≥0，∀k∈KI}，则问题（8）可转换[23]为

其中，hk(W，U，f，Φ)=lg|Wk|-tr(WkEk) +d.

转换后的问题（11）虽然增加了优化变量，但比问题（8）更易处理.利用BCD 算法来解决此问题.首先，对于给定的Wk、Φ和f，使hk(W，U，f，Φ)对Uk求一阶导数，并令其一阶导数等于0，可得Uk的最优解为

同理，固定Uk、Φ和f，使hk(W，U，f，Φ)对Wk求一阶导数，并令其等于0，可得到Wk的最优解为

2.2 预编码矩阵的优化

本研究通过固定W、U、Φ来优化预编码矩阵f.将式（10）代入问题（11），并将f的无关项去掉，可得

由于目标函数和最小能量约束都是非凸的，为将问题（14）转换成一个等价的凸问题，利用不等式[27]CAHdiag(BBH)A≥BHdiag(ACAH)B，可将目标函数转换成凸形式，即将问题（14）中的目标函数转换为

接着采用连续凸逼近（successive convex approximation，SCA）方法解决最小能量约束问题[28].通过一阶泰勒展开来近似能量约束，可得

其中，fk(n)为第n迭代所得的解.能量约束（8c）可写成

经此将问题（18）转变为凸问题，再采用拉格朗日对偶乘子算法来求解[29].由于问题（18）是一个凸问题，满足强对偶条件，且对偶间隙为0，所以可通过解决其对偶问题来获得最优解.引入功率约束相关的拉格朗日乘子λ，则问题（18）的部分拉格朗日函数为

对偶函数F(λ)为

则对偶问题可表示为

在解决式（21）前，需先求解F(λ)的表达式.通过引入能量约束（17）的拉格朗日乘子μ，可得问题（20）的拉格朗日函数为

拉格朗日函数L(f，μ)对fk求一阶导数，并令其等于0，可得到fk的最优解为

其中，μ满足约束（17）的互补松弛条件，即

当μ=0时，如果满足下列条件

然后，对对偶问题（21）进行求解，找到最优的λ.λ应满足约束（17）的互补松弛条件，即

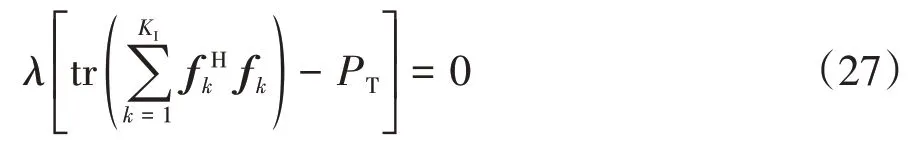
当λ=0时，如果满足下列条件

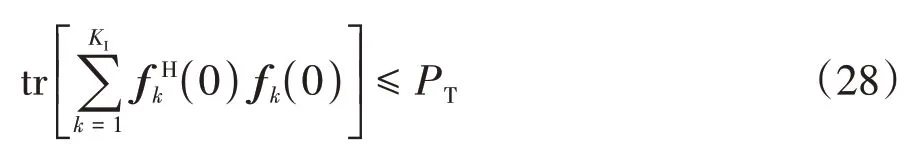
则可得到对偶问题的最优解为fk(0).若不满足条件（28），则假设在λ处求得问题（21）的最优解，有

由于μ的表达式过于复杂，难以得到P(λ)的表达式，本研究通过证明可得到P(λ)是一个单调递减函数（证明过程请扫描论文末页右下角二维码查看补充材料证明S1），再使用二分法算法可找到最优的λ.二分法算法详情请扫描论文末页右下角二维码查看补充材料图S1.图S1对λ＞0的情况提供了解决问题（18）的详细步骤.

图2给出了SCA算法的详细步骤，解决了问题（14），并得到了基站预编码矩阵的最优解.

图2 SCA算法伪代码Fig.2 SCA algorithm pseudocode.

定理1 由算法1 产生的{f(n)，n=1，2，…}序列会收敛于问题（14）的卡罗需-库恩-塔克（Karush-Kuhn-Tucker，KKT）最优点.

【证】与文献[29]证明相似，在此不再赘述.

2.3 相移矩阵的优化

在本小节中，将固定其他优化变量来优化相移矩阵Φ.将式（10）带入问题（11），并去除Φ的无关项，可得相移角的优化问题

为更好地处理优化问题，将相移矩阵Φ的对角元素用矩阵ϕ=[ϕ1，ϕ2，…，ϕM]T表示，取矩阵恒等式[28]，则有

其中，χ=Zr◦C2；Q2=Q0-tr(ZbFˉ)；为将能量约束式（36）变成凸形式，可使用SCA 算法.在ϕ(n)处将式子（36）一阶泰勒展开，可得

其中，（n）表示第n次迭代；

因此，问题（37）可改写为

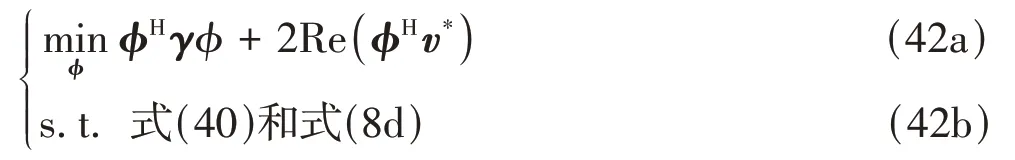
接下来，利用最优最小化（majorizationminimization，MM）算法[30]求解优化问题（42）.MM算法包括2个步骤：①找到一个局部逼近目标函数的替代函数，且在当前点处两个函数的差最小.②最小化替代函数.在替代函数达到最小值处，重复步骤①和②，直到目标函数与替代函数在当前点的值低于一个阈值，就可得到目标函数的最小值.

MM 算法最重要的步骤在于如何找到一个合适的替代函数，为此，本研究引入引理1[31].

引理1对于给定的ϕ(n)，对于任意的ϕ都满足不等式

其中，X=λmaxIM，λmax是γ的最大特征值；IM为M阶单位矩阵.

定义y(ϕ|ϕ(n))为替代函数，有

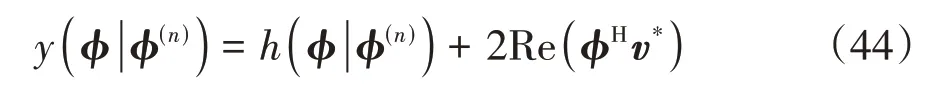
在替代函数y(ϕ|ϕ(n))中，ϕHXϕ=λmaxM为常量，可舍去，问题（42）可改写为

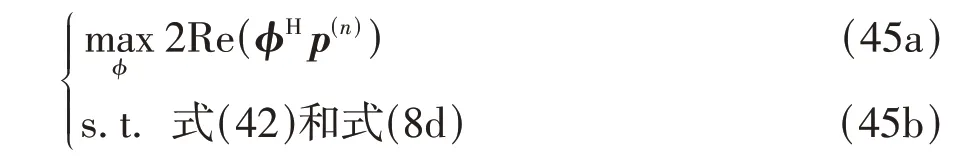
其中，p(n)=(λmaxIM-γ)ϕ(n)-v*，由于约束（41），和约束（8d）是非凸的，导致问题（45）也是非凸问题，因此不能使用的格朗日方法来求解.

文献[32]提出了一种等价方法，在约束（41）左边引入非负的辅助矢量q.

对于给定的q，该优化问题的全局最优解为

任意q都应当满足约束（41）的互补松弛条件

则有q*=0.若不满足式（49），则q*满足J(q*)=Q3.可以证明，J(q)是一个单调递增的函数（证明与补充材料S1类似，在此不再赘述），再通过二分法算法求得q*（详情请扫描论文末页右下角二维码查看补充材料图S2），提供了算法步骤，解决了问题（46）.

MM联合SCA算法详情如图3.

图3 MM算法伪代码Fig.3 MM algorithm pseudocode.

2.4 BCD算法求解全局最优解

图4 提供了全局性BCD 算法求解问题（8）的详细步骤.其中，R(f(n)，ϕ(n))为问题（8）目标函数第n次迭代的值.

图4 BCD算法伪代码Fig.4 BCD algorithm pseudocode.

定理2由算法3 产生的{R(f(n)，ϕ(n))，n=1，2，…}序列会收敛于问题（14）的KKT最优点.

【证】与文献[32]证明相似，在此不再赘述.

3 仿真结果

对考虑硬件损耗的IRS 辅助MIMO 的携能通信系统进行仿真，如图5.将基站设置在（-200，0）m处，设置能量收集器4 个，信息接收者3 个，让它们分别随机分布在以（5，0）m 和（0，0）m 为圆心，半径分别为4 m 和2 m 的圆中.同时，将IRS 设置在能量收集器附近（-195，5）m.仿真参数设置如表1.

表1 仿真参数Table 1 Simulation parameters

图5 IRS辅助的SWIPT系统仿真模型Fig.5 IRS aided SWIPT system simulation model.

大规模路径损耗模型建模为

其中，Lp0为参考距离D0处的路径损耗；D为链路的距离（单位：m）；α为路径损耗指数.将基站到信息接收者和能量收集器的信道都设置为瑞利衰落，其余信道为莱斯衰落.从IRS到能量收集器的小规模信道可建模为

其中，βIRS，ER为莱斯系数；分别为视距传输和瑞利衰落/非视距传输信道.

图6给出了不同反射单元数量M情况下BCD算法的收敛情况.从图6可见，BCD算法收敛速度很快，只需要几次迭代就可以实现算法收敛，且M越大，收敛的WSR越大.

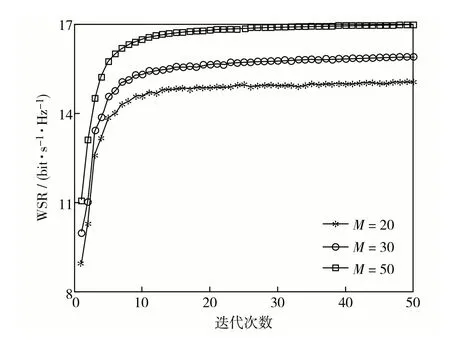
图6 BCD算法收敛图Fig.6 Convergence of the BCD algorithm.

接下来，将本研究与一些基准方案进行比较，以验证本研究方案的优势.方案如下：①MMIRS为本研究针对IRS辅助SWIPT系统中的硬件损耗而提出的MM 算法鲁棒波束形成设计；②MMIRSNonrobust为MM算法主动波束形成设计，但忽略了IRS 辅助的SWIPT 系统中的硬件损耗；③NonIRS为使用鲁棒波束形成设计来优化，但没有IRS辅助的SWIPT 系统中的硬件损耗；④NonIRS-Nonrobust为在无IRS辅助的通信系统中忽略硬件损耗的简单波束形成方案；⑤RandIRS 为针对IRS 辅助SWIPT系统中的硬件损耗而提出的随机相移算法鲁棒波束形成设计；⑥RandIRS-Nonrobust 为随机相移算法主动波束形成，但设计忽略了IRS辅助的SWIPT系统中的硬件损耗.

图7为在反射单元数量M=50发射的最大功率PT=15 W 的情况下，不同硬件损耗系数下最小收集能量Q0对WSR 的影响.由图7 可见，硬件损耗系数越大，对系统干扰就越大，WSR 越小；并且在用户端硬件损耗的影响要比基站端硬件损耗的影响大很多.

图7 不同最小能量约束阈值下硬件损耗对WSR的影响Fig.7 The effect of different hardware loss coefficients on WSR under the harvested power requirement.

图8为在M=50，Q0=2×10-4情况下，基站发射功率Ps对WSR 的影响.由图8 可见，无论在有无IRS 的系统中，随着基站发射功率Ps的增加，WSR 都增大，且当Ps增加到一定值时，WSR 增大趋势越来越平缓.这是因为由硬件损耗产生的干扰是与基站发射功率成比例的，当基站发射功率函数达到最大值时，信息接收者的WSR 也会存在一个最大值.虽然使用随机相移算法可一定程度上提高系统WSR，但提升效果远不如本研究提出的MM算法，在基站发射功率相同的情况下，WSR 最大差值达到了4 bit·s-1·Hz-1.

图8 不同方案在基站发射功率下的性能比较Fig.8 WSR versus the BS maximum transmit power requirement.

设PT=15 W，Q0=2 × 10-4，图9 给出了反射单元数量对WSR 性能的影响.由图9可见，IRS 辅助系统的WSR 值随M的增大也越来越大.在没有IRS 辅助系统中，鲁棒性设计要比非鲁棒设计的WSR 高将近5 bit·s-1·Hz-1，表明在考虑硬件损耗的SWIPT系统中鲁棒性设计可大幅提高系统性能.

图9 不同方案在反射单元数量下的性能比较Fig.9 WSR versus the number of phase shifters.

结语

在IRS辅助的SWIPT系统中考虑收发器的硬件损耗，对该系统的信息接收者加权和速率进行了鲁棒性研究，提出了一种快速收敛的BCD 算法，对基站的预编码矩阵和IRS的相移矩阵交替优化.在优化子问题中，提出了一些低复杂度的算法进行求解.仿真结果表明，在考虑硬件损耗的携能通信系统中，本研究所提出的MMBCD 算法比传统随机相移算法具有更强的鲁棒性，收发器硬件损耗会影响系统性能，且信息接收端的硬件损耗要比基站发射端的硬件损耗对系统的影响更大.