基于AVMD与SMA-SVM的滚动轴承故障诊断
杨东博 陈长征
(沈阳工业大学)
0 引言
随着人们环保意识的增强,以及对传统能源储量不断减少的担忧,风电装机容量正在全世界迅猛增长[1]。而轴承作为风电机组的重要零件,其故障与否直接关系着整个系统运行的稳定性。由于受各种外界因素的影响,只有10%~20%的轴承能达到它们的设计寿命[2]。若轴承故障没能及时发现并维修,可能产生更加严重的后果,造成经济损失。因此,滚动轴承的故障诊断具有重要的意义和价值。目前,特征提取和分类识别 是轴承故障诊断的两大重要研究方向。
为了解决复杂信号的故障特征提取问题,Huang N E[3]等提出了经验模态分解(empirical mode decomposition,EMD)方法,但是该方法会出现模态混叠现象、端点效应以及欠包络、过包络等问题。Gilles J 提出了经验小波变换方法,但EWT 在面对复杂频谱时,存在过切分问题[4]。K Dragomiretskiy等人[5]提出了一种变分模态分解算法(variational mode decomposetion,VMD)的信号处理方法。VMD 基于信号的局部特征时间尺度,可有效处理非平稳、非线性的信号,无需如小波等方法事先定义合适的分析基函数[6]。VMD能有效避免EMD的模态混叠等问题,但是该方法的本征模态分量需要有一定的处理经验或多次人为试验来进行确定。
目前,轴承等部件的故障诊断依然靠人工通过频谱波形图来进行判断,虽然也可以定位故障位置,但是这种方法精度不高,需要大量的经验,且效率极低,具有很大的局限性。因此,国内外专家学者将基于统计学理论的支持向量机(support vector machine,SVM)应用于故障诊断之中[7,8]。为了进一步提高故障识别的准确率,诸多学者用优化算法对支持向量机的参数进行寻优,常见的有果蝇算法[9]、遗传算法[10]和粒子群算法(particle swarm optimization,PSO)[11-12]。然而上述的智能算法在进行滚动轴承故障识别时,均会出现一些不够理想的情况,比如寻优速度慢、寻优时间长等。另外,调节参数多,以及容易陷入局部最优值等问题,还会导致分类的准确率不高。
基于以上问题,本文引入了一种非人为确定VMD分解IMF 个数的方法(adaptive variational modal decomposition,AVMD)来确定最佳分解个数,并提出一种基于VMD样本熵与SMA-SVM 相结合的故障诊断方法,提出的优化方法可加快收敛且可以跳出局部最优,通过转子实验台声音数据进行实验验证,证明了该方法在故障识别领域优于其他传统方法。
本文第一部分介绍了自适应变分模态分解和样本熵的基本原理,第二部分在详细阐述黏菌优化算法的基础上,提出了该算法优化支持向量机的基本步骤,第三部分建立了AVMD-SMA-SVM诊断模型,为后续实验部分打下基础,第四部分通过实验对比得出该模型要优于传统优化模型的结论。
1 信号的特诊提取
1.1 自适应变分模态分解
VMD 是一种信号分解估计的方法,该方法以带宽之和最小寻找K个本征模态函数,假设原信号可分解为多个窄带IMF分量,构造出如下约束变分模型:
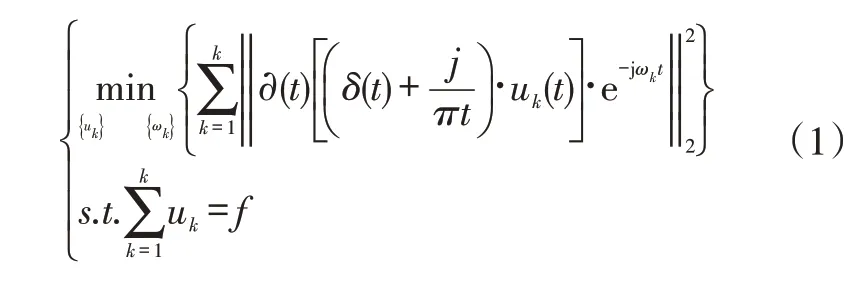
式中,f为原始信号;ωk为各模态分量的中心频率;uk为第k个IMF分量。
首先,对uk(t)进行希尔伯特变换得到单边谱,然后调节预估的中心频率,并将其频谱调整到相应的基带上。引入二次惩罚因子α和拉格朗日乘子λ(t),将原变分约束模型转换为非变分约束模型,得到以下增广拉格朗日函数:
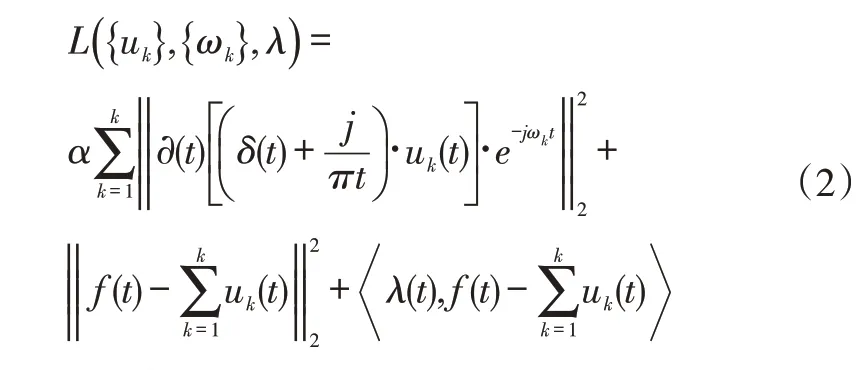
式中,α为二次惩罚因子;λ为Lagrange因子。

VMD 有一个重要参数K,在分解前要预先设定模态数K,在进行VMD分解时,应当选择合理的模态数K,若选择不合理,则会出现过分解和欠分解的现象,并且模态数要根据经验来选定。
文献[13]提出了一种自适应确定模态数K的方法,即自适应变分模态分解(AVMD)。
该方法通过频谱极值点和自适应阈值之间的大小关系来确定模态数K,具体过程如下:
1)截取经傅里叶变换后频谱信号的一半;
2)确定局部极大值点(max)与极小值点(min),连接所有极值点组成包络线,进一步寻找该上下包络线的极大值点(Lmax)与极小值点(Lmin),公式如下:
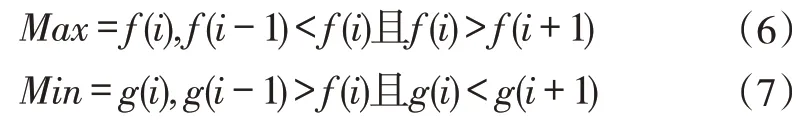
其中,f(i)和g(i)为第i个频谱值。
3)设定自适应的阈值,该值可以随着极值点k的变化而变化,以抵抗强噪声的干扰,公式如下:
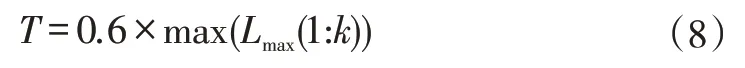
4)将上包络线中连续两个极大值点间的极小值点标记为位置P。
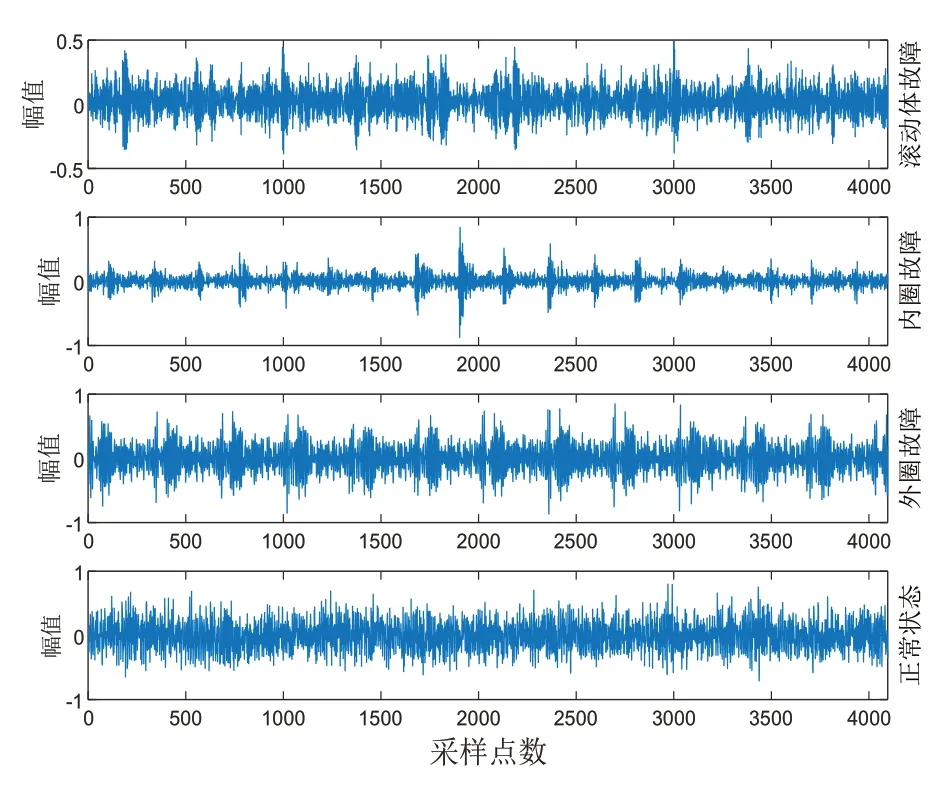
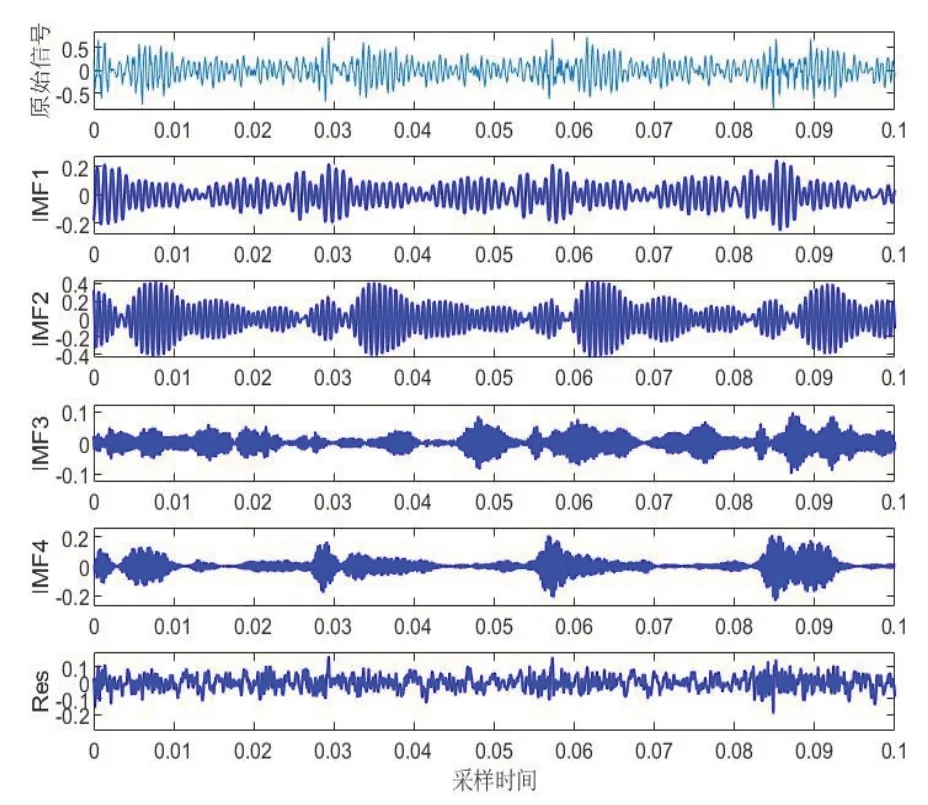
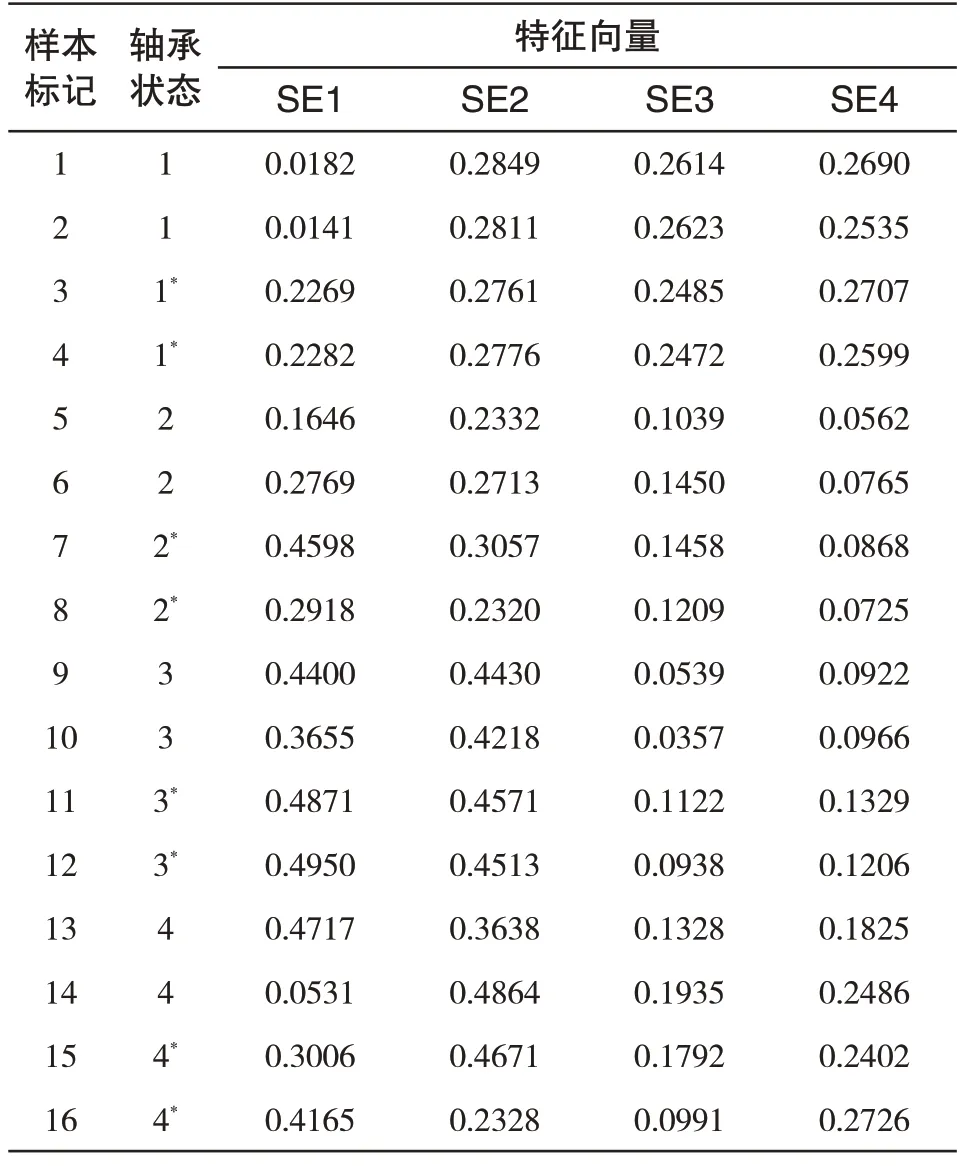
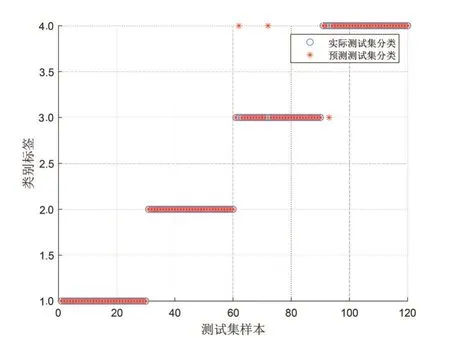
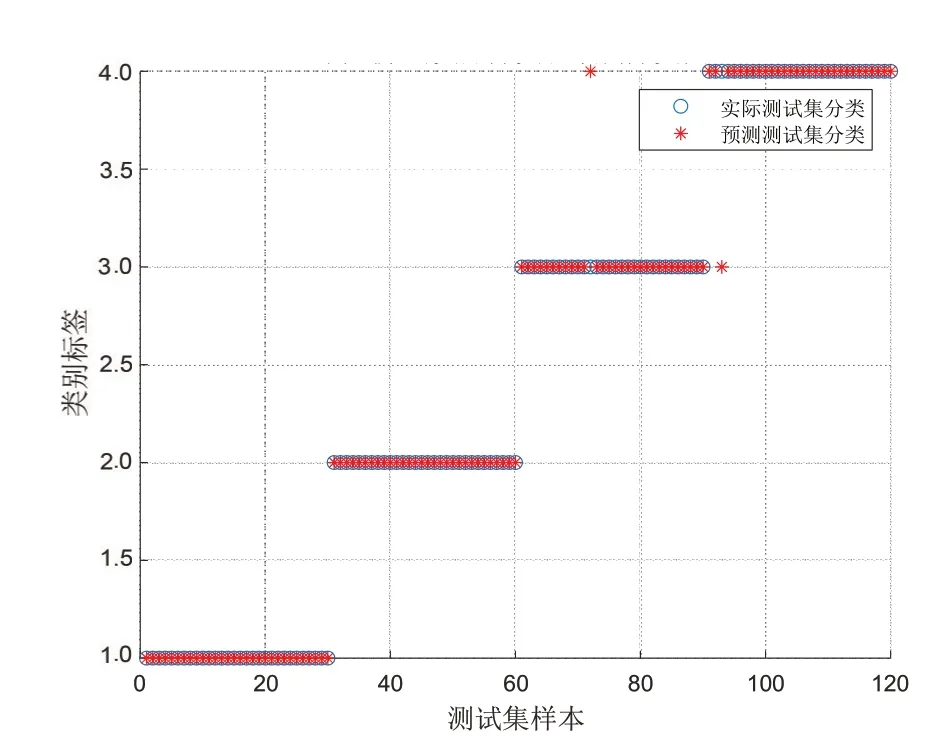
5)寻找上下包络线位置P对应的最小值S(其中S>T)和极大值B(其中B 6)执行上文进行VMD分解。 样本熵(Sample Entropy,SampEn)是由Richman,JS等[14]提出的,从时间序列的复杂性角度出发,定量描述系统的复杂度和规则度,时间序列复杂度越低,样本熵数值越小,时间序列复杂度就越高,数值就越大[15]。 已知一时间序列样本X(n),求其样本熵公式如下: 1)将时间序列组成m维向量序列,得到状态向量 式中,1 ≤i≤N-m+1 2)定义X(i)、X(j)两向量之间距离定义为Dij 式中,0 ≤k≤m-1 3)设置相似容限阈值r,统计距d[X(i),X(j)]小于等于r的数目,记作Bi,并计算所有平均值 4)将模式维数m加1 5)时间序列估计样本熵值为: 支持向量机(supported vector machine,SVM)是由Vapnik[16]在1995年提出的一种模式识别方法。在对非线性数据集的分类过程中,通过引入核函数的方法,使低维空间中的线性不可分的数据映射到高维空间中,在高维空间中寻求最优的分类超平面[17]。径向基核函数具有良好的非线性、局部性能以及抗干扰等特点。因此,在SVM的核函数的选取上,本文中SVM所采用的核函数均为径向基核函数。 在进行SVM分类时,惩罚因子C和核函数参数σ的大小决定了最后分类结果准确与否。 Li等[18]在2020年提出了黏菌优化算法,该方法根据自然界中黏菌寻找食物的过程,使用自适应权重来模拟基于生物振荡器的黏菌传播波产生正反馈和负反馈的过程[19],形成具有优异探索能力和开发倾向的食物的最佳路径。该数学模型如下: 1)接近食物 黏菌可以通过气味来接近食物,为了模拟这种行为,提出以下规则: 式中,S(i)为适应度;DF为所有迭代过程中的最佳适应度;Condition为排在种群数前一半的个体;r为在[0,1]区间上的一个随机数值;bF和wF为最优和最差适应度值;SmellIndex为适应度值序列。 2)包裹食物 黏菌在搜索食物时,受食物气味浓度的影响,生物振荡器产生不同信号,黏菌静脉接触的食物浓度越高,波动越强,细胞质流动越快,静脉就越厚,反之亦然。黏菌更新位置的公式如下: 式中,LB,UB为上下搜索范围的边界值;rand和r为[0,1]内的随机数。 黏菌算法优化支持向量机的具体优化步骤如下: 1)进行参数设置,设置SMA 算法中黏菌种群大小和最大迭代次数; 2)初始化黏菌位置,每一个黏菌位置包括C,σ; 3)计算个体的适应度值,并进行排序; 4)更新最佳位置和最优适应度所产生新的黏菌位置; 5)判断迭代次数是否达到设置的阈值,若不满足迭代条件,则重复直至输出最优个体; 6)输出最优个体适应度值和最佳位置,提取最优参数C,σ。 基于AVMD 与黏菌优化算法优化支持向量机故障诊断流程如下,总体流程示意图如图1所示。 图1 流程图Fig.1 Flow chart 1)利用AVMD将采集得到的轴承声音信号分解为若干IMF; 2)计算各分量的样本熵作为特征向量; 3)随机分为训练样本和测试样本; 4)将测试样本输入到SMA 优化后的SVM 中进行故障诊断。 为了检验上述方法的准确性,采用图2实验台轴承的声音信号进行研究。轴承型号为UC205,传感器类型为MPA231声音传感器,过程中电机转速为1700r/min。 图2 转子实验台Fig.2 Rotor test rig 轴承状态分别为滚动体故障、内圈故障、外圈故障和正常状态,通过麦克风采集滚动轴承声音信号的采样频率为12kHz,采样点数为4096个,其中,四种状态下的振动信号各60组,将每种状态数据随机分为两组,即训练样本与测试样本各30组。 实验中将滚动体故障、内圈故障、外圈故障和正常状态四种情况分别用标签1,2,3,4表示。其中,各状态时域波形图如图3所示。 图3 各种状态下的时域波形图Fig.3 Waveform diagram under various conditions 将上述数据分别进行AVMD 算法进行分解,选取前4个IMF,图4为滚动轴承外圈故障时域的分解结果。 图4 AVMD处理结果Fig.4 AVMD decomposition results 求取各组信号的IMF,并计算其样本熵,因为篇幅关系,此处给出部分分解后的样本熵特征向量值,见表1。 表1 不同轴承状态下的部分样本熵数值Tab.1 Entropy values of some samples under different bearing conditions 将样本熵作为特征向量分别输入到GA-SVM、PSO-SVM和SMA-SVM的模型中,进行对比实验。三种模型的分类准确率如图5~7所示。 图5 GA-SVM模型的分类准确率Fig.5 Classification accuracy of GA-SVM model 图6 PSO-SVM模型的分类准确率Fig.6 Classification accuracy of PSO-SVM model 通过上图可知,遗传算法GA优化支持向量机和粒子群算法PSO 优化支持向量机识别滚动轴承滚动体故障和内圈故障时均没有出现失误,但是在对外圈故障和正常状态识别时会出现混淆,即容易出现识别为相互状态的情况,这种对故障识别是极为不利的。相比而言,SMA-SVM 模型识别准确率更高,只有一组数据识别错误,也未出现这种情况。 为了使实验更具有说服力,在相同数量的训练集与测试样本的情况下,分别将3 种模型均进行50 次实验,并记录平均分类准确率以及平均寻优时间,结果如表2所示。 表2 模型对比结果Tab.2 Model comparison results 通过表2 和图5~图7 可以看出,SMA-SVM 模型相比于GA-SVM 和PSO-SVM 而言,除了分类准确率更高以外,在寻优速度上也具有一定的优势。 图7 SMA-SVM模型的分类准确率Fig.7 Classification accuracy of SMA-SVM model 针对传统优化算法优化支持向量机在轴承故障诊断方面,分类速度慢,分类准确率低等问题,提出了一种自适应变分模态分解与黏菌算法优化支持向量机相结合的故障诊断方法(AVMD-SMA-SVM)。首先自适应选取模态分解数量,然后计算得到的IMF的样本熵数据作为特征向量输入到SMA-SVM模型中,通过对轴承诊断分析,得到如下结论: 1)将VMD算法用于故障诊断中,将信号分解为一系列不同带宽的分量,避免模态混叠,且通过自适应变分模态分解,非人为选取合适的分解数量,为后续故障分类的准确性打下了基础。 2)通过计算各分量的样本熵,确定各分量的复杂性关系,实验结果表明,该特征向量可有效用于轴承的故障诊断。 3)所提出的SMA-SVM 模型相比于传统优化模型在轴承故障诊断寻优速度上具有一定的优势,并拥有更高的分类准确率,在其他方面也可借鉴此方法。1.2 样本熵



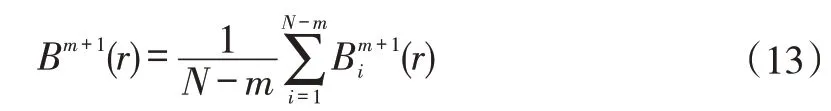
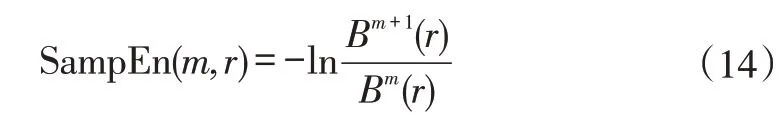
2 黏菌优化算法优化支持向量机
2.1 支持向量机
2.2 黏菌优化算法

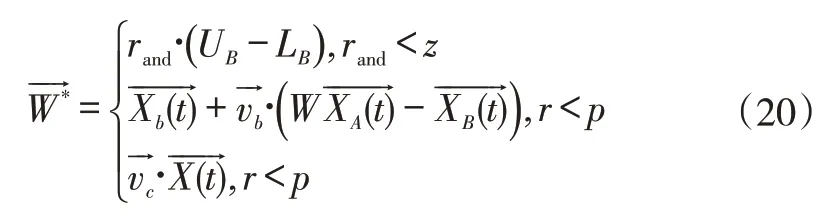
2.3 黏菌算法优化支持向量机步骤
3 AVMD-SMA-SVM诊断流程

4 实验结果与分析
4.1 实验数据准备

4.2 实验结果分析


5 结论
- 风机技术的其它文章
- 机匣处理在无喷嘴径流涡轮叶片抑振中的应用*
- Study on Loss Quantitative Analysis Methodology for Highly-loaded Transonic Fan*
- Influence of Change Law of Blade Leading-Edge Ellipse Ratio on Inception Cavitation Performance of Centrifugal Pump*
- 带诱导轮的离心式航空燃油泵空化特性分析*
- Optimization Design of Air Conditioning Outdoor Unit Top Plate Based on Orthogonal Test
- 重燃透平叶片真实内部冷却通道的传热特性研究*

