机匣处理在无喷嘴径流涡轮叶片抑振中的应用*
潘 镭 杨名洋 Shota Murae Wataru Sato Naoto Shimohara Akihiro Yamagata
(1.上海交通大学;2.IHI Corporation)
0 引言
发动机小型化与涡轮增压相结合已成为应对日益严格的排放法规的有效手段[1-3]。径流涡轮是涡轮增压器的重要部件,其性能在很大程度上决定了发动机的整体性能。涡轮叶片的高周疲劳(HCF)问题是增压器损坏最常见的原因,主要由叶轮与定子之间流场动-静干涉作用引起[4,5]。随着人们对高膨胀比、高效、快速响应的要求日益提升,径流涡轮朝薄叶片、小动-静间隙的方向发展。然而,这种发展趋势将使叶片结构强度降低并引起更强的气动激振力,进一步加剧叶片因高周疲劳损坏的风险[6-8]。因此,为了设计高效、高可靠性的径流涡轮,需要重点发展叶片抑振方法。
目前,学术界对带喷嘴径流涡轮叶片的气动激振问题的研究较为广泛。对于带喷嘴涡轮,喷嘴与叶轮之间的动-静干涉引发了气动激振。多种流场现象被认为是潜在的气动激振源,包括喷嘴激波、尾迹、间隙流和势场[9-11]。需要指出的是,喷嘴激波是很强的气动激振源,其主要出现在高负荷、喷嘴小开度的条件下,对涡轮安全构成较大威胁。雷新国研究了喷嘴表面开槽对激波的影响。实验和仿真结果均表明,开槽可以显著削弱激波强度[12]。
无喷嘴径流涡轮由于结构紧凑、高效区宽广等优点,在车用增压器上应用广泛。然而,与带喷嘴涡轮相比,目前学术界对无喷嘴涡轮气动激振的研究很少。对于无喷嘴涡轮,叶片气动激振力来自于蜗壳几何的周向非对称性所引发的周向流场畸变[13,14]。部分学者通过重新设计叶型以减小应力。Naik采用数值方法研究了叶片沿叶高方向的厚度分布对应力的影响。结果表明,新叶型高周疲劳损坏的风险降低了30%,然而效率也降低了1%[15]。另一些学者尝试改进蜗壳几何以降低气动激振力。Kitson开发了一种新的蜗壳几何,削弱叶轮进口的流场畸变。实验和仿真结果均表明,新蜗壳使叶片应变降低了70%[16]。Smith实验研究了蜗壳关键几何参数对叶片振动的影响。结果表明,通过合理调整几何参数,可使叶片振幅下降85%,且不牺牲涡轮气动性能[17]。然而,设计新蜗壳具有周期长、通用性差等劣势。综上所述,当前抑振方法无法兼顾气动性能、周期与通用性,需要开发新的抑振方法。
本文探究基于机匣处理(Casing Treatment)的无喷嘴径流涡轮叶片抑振方法。本文分为以下几个部分:1)单向流固耦合数值方法介绍及实验验证;2)提出机匣处理抑振方法,并研究机匣几何参数对叶片振动的影响规律及其机制。
1 数值方法
采用日本IHI 集团的无喷嘴径流涡轮作为本文的研究对象。图1显示了涡轮的主要部件,表1列出了涡轮的主要几何参数。

图1 涡轮主要部件Fig.1 Main components of turbine

表1 涡轮几何参数Tab.1 Geometric parameters of turbine
考虑到涡轮叶片振幅很小,对流场的影响不大,采用单向流固耦合作为数值计算方法[18]。该方法分别求解流体域与固体域,计算资源显著低于双向耦合法。单向法的计算步骤为:首先进行非定常CFD计算,然后从CFD 结果中提取气动激振力并施加在有限元模型上,进而计算叶片振动响应。在该涡轮的转速范围内,由4~6阶激励阶次(EO)所引发的一阶弯振对涡轮安全的威胁最大,不失一般性,本文研究4EO。
采用ANSYS CFX进行非定常CFD计算。图2(a)显示了流体计算域,包括进口段、蜗壳、叶轮和扩压器。扩压器长度为8 倍叶轮直径,以确保出口不会发生回流,提高计算准确度。采用六面体结构化网格划分叶轮通道,如图2(b)所示。采用四面体非结构化网格划分其余流体域。蜗壳网格如图2(c)所示。每个叶轮通道的节点数为573000,蜗壳节点数为639000。固壁面第一层网格厚度设置为0.01mm,确保Y+足够低,以精确模拟壁面附近的流动。湍流模型采用k-ε 双方程模型。进口总温为923.15K,出口静压为1bar。壁面设为绝热、无滑移条件。采用滑移网格(transient rotorstator)处理非定常计算的动-静交界面。涡轮转速为4阶临界转速。时间步长为叶轮旋转2°所需的时间。计算总时长为叶片旋转7周所需的时间,以确保流场具有良好的周期性。均方根(RMS)残差收敛标准设置为1.0×10-5。采用定常计算结果作为非定常计算的初值,达到快速收敛的目的。
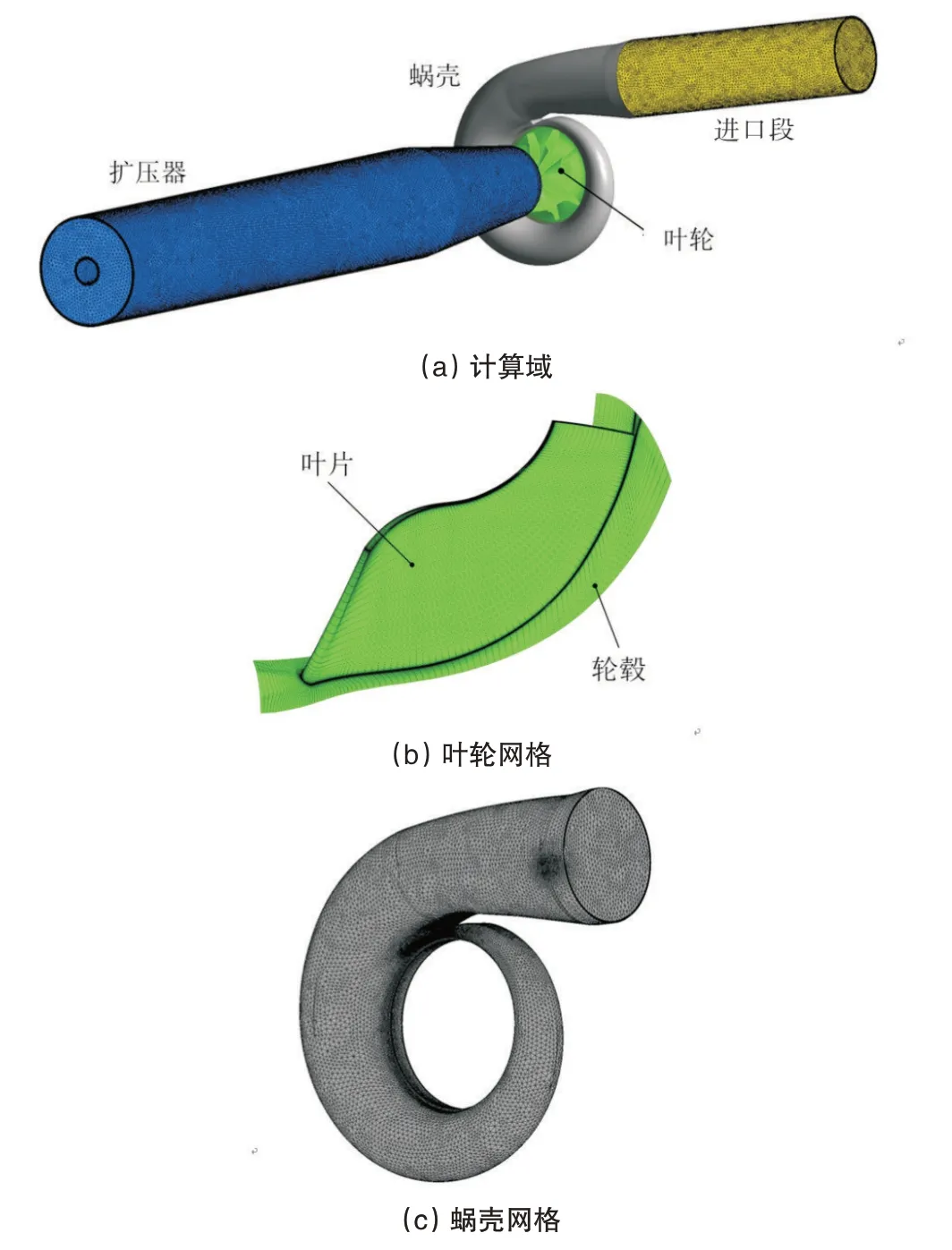
图2 流体计算域和网格划分Fig.2 CFD fluid calculation domains and meshing
有限元分析(FEA)包括两部分:模态分析和谐响应分析。叶轮的有限元模型如图3(a)所示,采用10 节点四面体划分网格,节点数为1458000。首先开展模态分析,得到叶片一阶弯振的固有频率和振型。图3(b)显示了叶片的振型,采用无量纲振幅表示。谐响应分析分为以下几步:(1)从非定常CFD结果中提取叶片表面的瞬态压力;(2)对瞬态压力作FFT分解,得到4阶谐波分量;(3)将4阶谐波压力施加在有限元叶片表面上,进行谐响应计算,得到叶片振幅。阻尼采用恒定值。
将振幅预测值与实验值对比,以验证数值方法的可靠性。采用叶尖定时法,在IHI集团的涡轮增压器测试台架上测量叶片振幅。台架照片如图3(c)所示。在叶轮出口周向位置处安装5个光学传感器,以监测叶片振动。图3(d)显示了振幅预测值与实验值的对比。随着膨胀比升高,实验值先减小,并在无量纲膨胀比1.00处达到极小值,然后持续增大。选取4个无量纲膨胀比作为仿真计算的工况:0.85,1.00,1.15,1.35。可以看出,预测值与实验值符合较好,特别是振幅与膨胀比之间的“V形”趋势被数值方法清晰地捕捉到了。因此,单向流固耦合数值方法是可靠的,其结果可用于接下来的分析讨论。

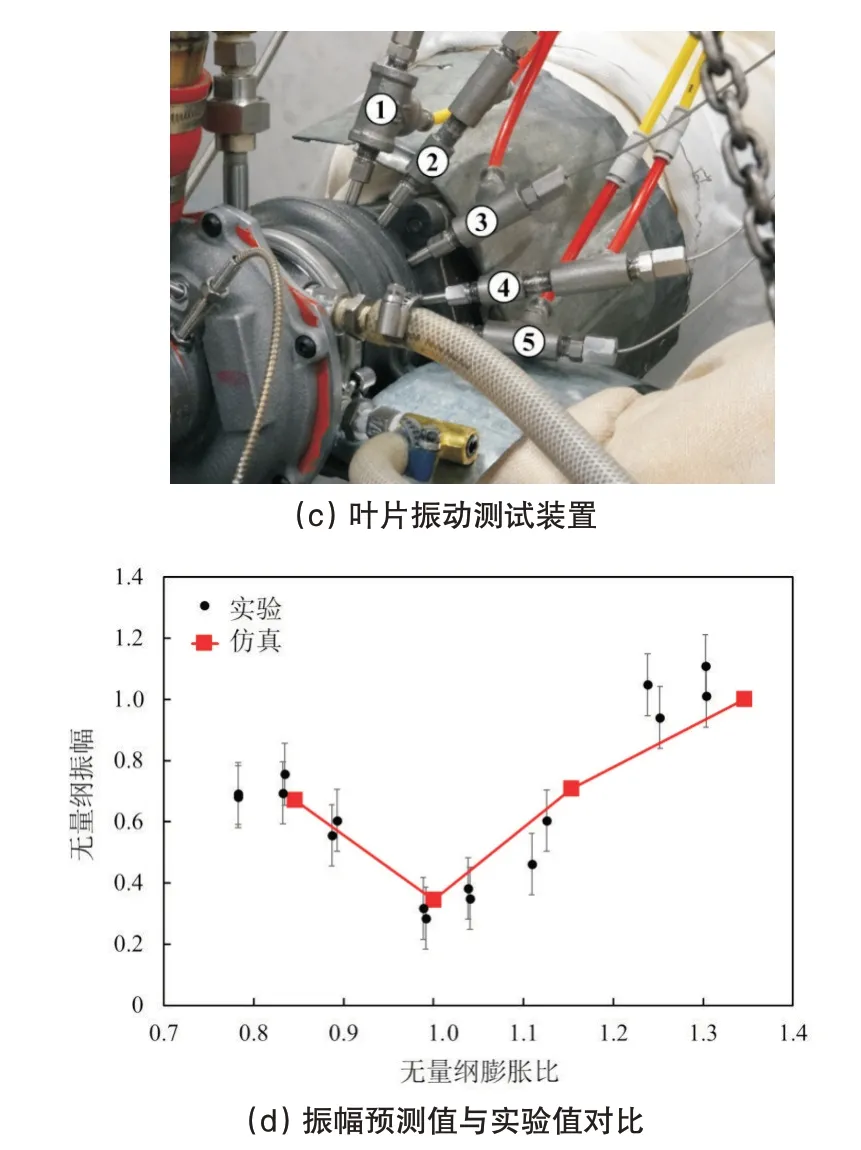
图3 有限元分析和数值方法验证Fig.3 Finite element analysis and validation of numerical method
2 抑振流动控制方法
本文的目标是提出一种新的抑振流动控制方法,以克服现有方法的缺陷。如图3(d)所示,叶片振幅在无量纲膨胀比1.35处达到最高,对涡轮安全运行的威胁最大。因此,重点研究涡轮在该膨胀比下的抑振方法。
2.1 广义力方法
叶片振幅由叶片表面的气动激振力的分布所决定。为了设计抑振流动控制方法,需要将激振力与叶片振动关联起来。采用广义力方法作为分析抑振问题的工具。该方法与传统分析方法(如能量法)相比,无需知道真实的振动参数,使分析过程得到简化。以下推导广义力的表达式。
叶片表面4阶谐波压力的复数形式(pˉ):

式中,A4和φ4分别为4阶谐波压力的幅值和初相位。
叶片表面一点的广义压力(pgen):

式中,Y是该点所对应的无量纲位移矢量,最大长度为1,如图3(b)所示。n是该点的单位法向量。
将广义压力在叶片表面积分,得到广义力Fgen:
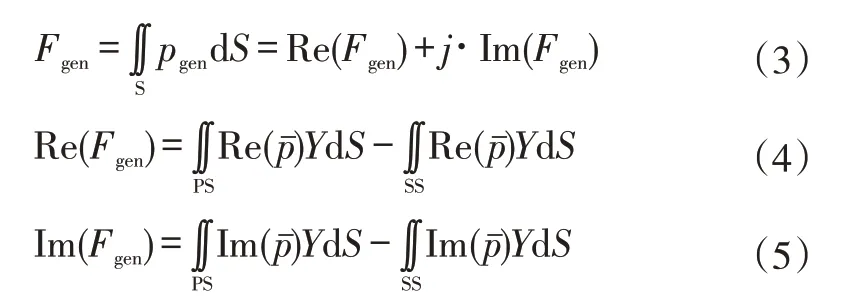
从广义力表达式得知,广义力为复数,可以在平面坐标中用矢量表示,如图4 所示。理论上可以证明,广义力长度与叶片振幅成正比,因此可以将其视为衡量振幅大小的量度。可以通过缩短广义力的长度来达到抑振的目的。如引言所述,修改蜗壳几何具有周期长、通用性低等缺点。从广义力的角度看,该方法的本质是通过削弱气动激振力来直接缩短广义力的长度。本文采用一种全新的思路,即不直接改变蜗壳对应的广义力,而是通过人为引入额外的广义力来抵消蜗壳的广义力。可以通过机匣处理的方式引入额外的广义力。具体而言,是在机匣壁面上设计沟槽,当叶片经过时,表面的压力会受到沟槽的扰动,产生额外的激振力。下文将详细讨论沟槽的设计方法。
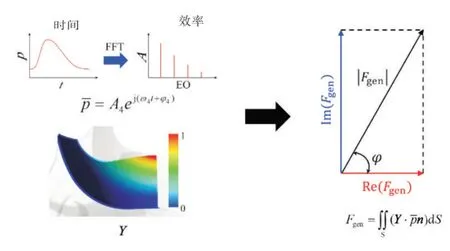
图4 叶片的广义力Fig.4 Generalized force of the blade
2.2 机匣处理简介
图5(a)~(c)展示了机匣处理的几何特征。考虑到机匣处理的目的是产生额外的4阶激振力以抵消蜗壳的4阶激振力,在叶轮周向上均匀布置4个轴向直槽。叶片在旋转一周的过程中,表面压力4次受到沟槽的干扰。直槽布置在叶片尾缘处,因为该处振幅高,激振力对叶片振动的影响最大。用相对角度α 表示沟槽和蜗舌之间的相对位置,其取值范围在0~90°之间。直槽的宽度用周向角β表示。直槽的轴向长度和高度分别用参数d1,d2和h表示。
图5(d)展示了广义力三角形,机匣处理后叶片的广义力命名为Ftotal,它代表蜗壳与直槽的共同作用。无机匣处理的广义力命名为Ftongue,因为其只由蜗舌决定。二者之差命名为Fcasing,它代表机匣处理对广义力的贡献,可以通过改变机匣处理的几何参数以调节该矢量的长度和相位。为了达到抑振目的,要尽可能使Fcasing和Ftongue大小相等方向相反,这样Ftotal的长度会显著缩短。
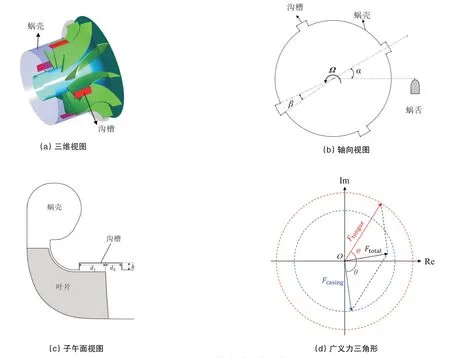
图5 机匣处理几何特征与广义力三角形Fig.5 Geometric characteristics of casing treatment and generalized force triangle
2.3 相对角的影响
相对角(α)表示直槽与蜗舌的相对位置,其决定了叶片表面压力何时受到直槽的扰动。可以推测该参数与Ftongue的相位密切相关。因此,需要重点分析相对角对叶片激振的影响。选取0°与45°两个角度作为研究对象,它们分别代表蜗舌与直槽的最近与最远距离。
图6显示了相对角对振幅的影响。可以看出,相对角对振幅影响显著。相对角为0°时,振幅相对于无机匣处理提高了145%;而相对角为45°时,振幅相对于无机匣处理下降了46%。可以推测振幅的差异来源于Fcasing相位的变化。为了验证该推论,图7显示了广义力三角形。当相对角为0°时,Fcasing与Ftongue方向接近一致,因此Ftotal的长度远大于Ftongue。相反,当相对角等于45°时,Fcasing与Ftongue方向几乎完全相反,二者相互抵消。注意到Fcasing的长度几乎不随相对角的变化而变化,这表明相对角主要影响Fcasing的相位而不是长度。

图6 相对角对振幅的影响Fig.6 Influence of relative angle on blade vibration amplitude
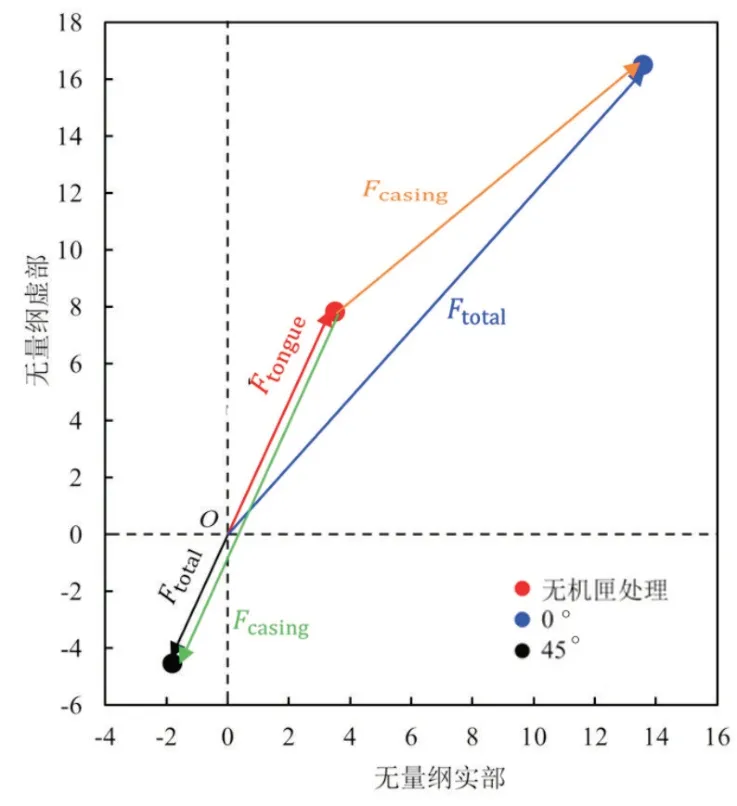
图7 相对角对广义力三角形的影响Fig.7 Influence of relative angle on generalized force triangle
由表达式(1)~(5)可知,广义力由激振力在叶片表面的分布决定,而激振力由压力作FFT分解得到。为进一步理解相对角对广义力三角形的影响,需要分析叶片表面的压力波形。考虑到高振幅区域的压力对振幅影响显著,将压力监测点放置在该处,如图8(a)所示。为突出机匣处理对压力的贡献,定义新参数“压力差pcasing”,表达式如下:
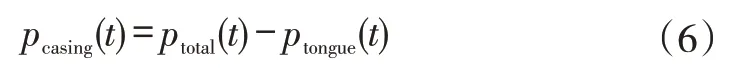
式中,ptotal(t)为机匣处理条件下的瞬态压力;ptongue(t)为无机匣处理条件下的瞬态压力;pcasing(t)的定义方式与Fcasing类似。
图8(b)显示了当相对角为0°时,A点压力差pcasing(t)在一个旋转周期内的变化。图中标出了蜗舌与4 个直槽的位置。可以看出,压力差的周期性不佳。该现象在吸力面表现得尤为显著,蜗舌附近的波形明显不同于远离蜗舌处的波形。该现象表明,靠近蜗舌处的直槽受到了蜗舌的干扰,二者的耦合作用使流场畸变程度进一步加剧,放大了激振效果,使振幅增大。该机制在图7 中反映为Fcasing与Ftongue方向相同。
图8(c)显示了当相对角为45°时,A点压力差pcasing(t)在一个旋转周期内的变化。与0°相比,该角度下的压力差呈现出良好的周期性。该现象表明,4个直槽对叶片压力的影响相似,靠近蜗舌处的直槽未明显受到蜗舌的干扰。可以推断,该角度下蜗壳与直槽的作用解耦,机匣处理真正起到了抵消蜗壳激振效应的作用。该机制在图7中反映为Fcasing与Ftongue方向相反。
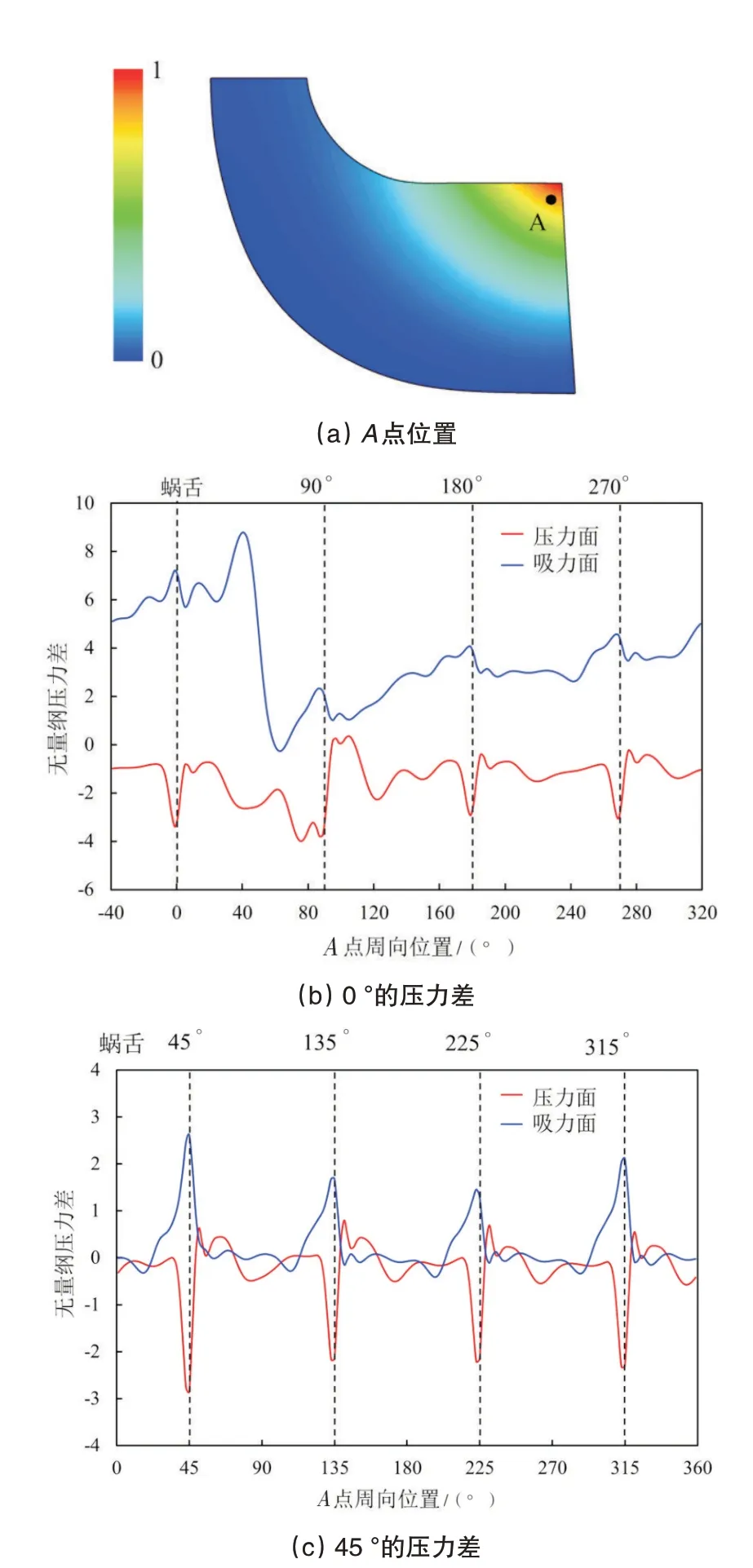
图8 机匣处理对叶片表面压力波动的影响Fig.8 Influence of casing treatment on pressure fluctuations on the blade
综上所述,45°可以视为相对角的最优值,用于机匣处理的设计。此外,CFD 结果表明,机匣处理后的涡轮性能(流通能力、效率)相对于无机匣处理几乎不变,相对变化值低于0.1%。这主要归因于对沟槽尺寸的严格限制。该结果证实了机匣处理可以在不牺牲涡轮性能的条件下抑制叶片振动。
2.4 直槽尺寸的影响
如上文所述,相对角主要对Fcasing的相位产生影响。虽然45°时Fcasing的相位达到最优值,为了进一步降低振幅,需要调节Fcasing的长度使其与Ftongue的长度相近。推测Fcasing的长度可能与直槽尺寸相关。本节研究直槽尺寸参数对叶片激振的影响规律及机制。相对角设置为45°。
图9 显示了4 个尺寸参数对叶片振幅的影响。尺寸参数以2.3节中直槽的参数为基准作无量纲化,振幅以无机匣处理情况下的振幅为基准作无量纲化。结果表明,3 个参数d1,h,β对振幅影响较大。当d1从0.6 增至1.4时,振幅降低了77%。h和β对振幅的影响与d1相反。当二者为0.6时,振幅很小,但随着参数值的增加,振幅显著增大。然而,振幅对d2并不敏感,因为该参数代表了直槽在叶片尾缘下游的长度,对上游叶片表面的压力影响不大。值得注意的是,当h为0.6 时振幅最小,相比无机匣处理下降了94%。将该几何视为机匣处理在无量纲膨胀比1.35下的最优设计。
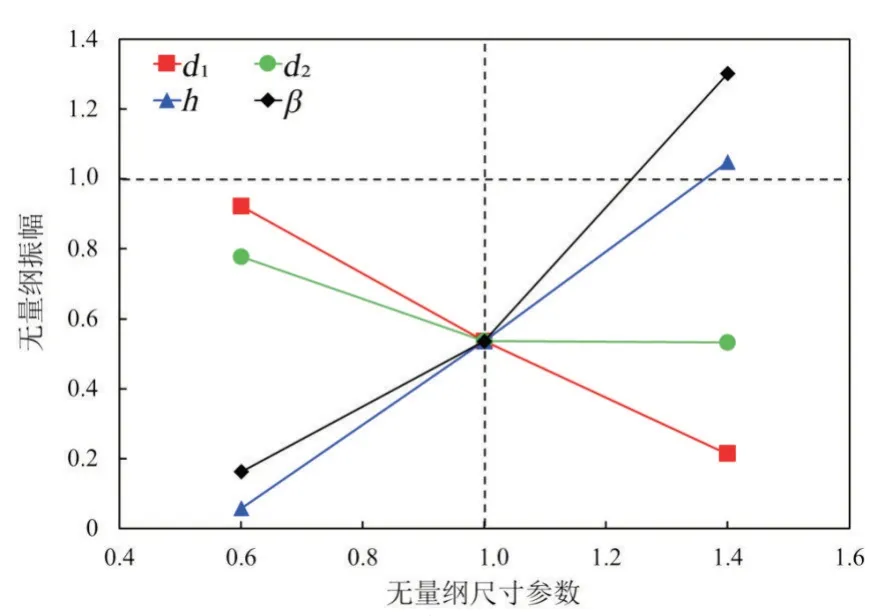
图9 尺寸参数对振幅的影响Fig.9 Influence of configuration parameters on amplitude
为理解振幅与尺寸参数的关系,图10显示了3个尺寸参数(d1,h,β)对广义力三角形的影响。可以发现,d1同时影响Fcasing的幅值与相位。当d1为0.6 时,Fcasing长度较长且位于Ftongue的左侧,此时Ftotal长度较长。当d1增加至1.0时,Fcasing朝逆时针旋转至Ftongue的反方向,导致Ftotal变短。当d1继续增加至1.4时,Fcasing进一步缩短且朝逆时针方向小幅旋转,导致Ftotal进一步变短。图10(b)解释了Fcasing相位变化的原因。直槽长度为d1的部分对叶片激振的影响可以集中到一个等效点E点上,当叶片经过E点时受到它的影响。E点和叶片的距离用周向角Δα表示。随着d1的增加,等效点向上游移动,Δα变小。因此,叶片会更早地受到等效点的激振作用,导致Fcasing逆时针转动。综上所述,Fcasing相位随d1的变化来源于直槽与叶片方向的不一致。然而,h和β只影响Fcasing的长度而不影响相位。当两个参数为0.6 时,Ftongue和Fcasing长度几乎相等,因此Ftotal长度很小。随着两个参数的增加,Fcasing变长导致Ftotal也变长。这解释了图9中振幅随两个参数的增加而持续增大。

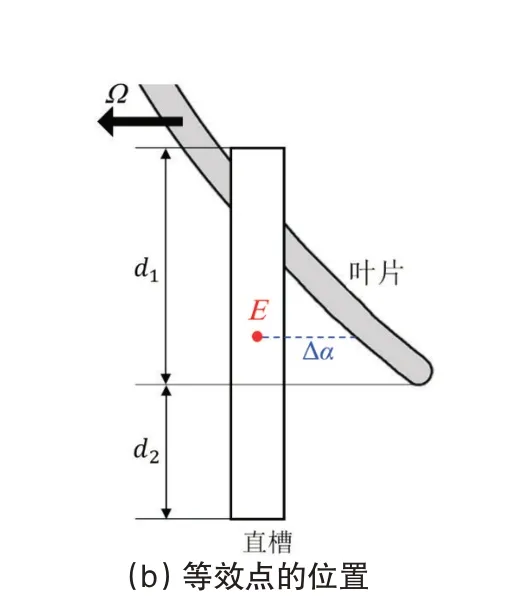
图10 直槽尺寸参数对广义力三角形的影响Fig.10 Influence of straight flute parameters on generalized force triangle
因为h和β只影响Fcasing的长度而不影响相位,极大地方便了直槽的最优设计,因此将这两个参数视为关键几何参数,需要研究二者对气动激振的影响机制。
图11 显示了关键参数对A点压力差的影响。随着参数值的增加,波形保持相似且在纵坐标方向上拉伸,该现象在压力面和吸力面均出现。由此推断,关键参数主要影响压力差的4阶谐波分量的幅值,且幅值与关键参数的值成正相关。由广义力表达式可知,Fcasing的相位不变且长度随着关键参数增加而变大,如图10(a)所示。
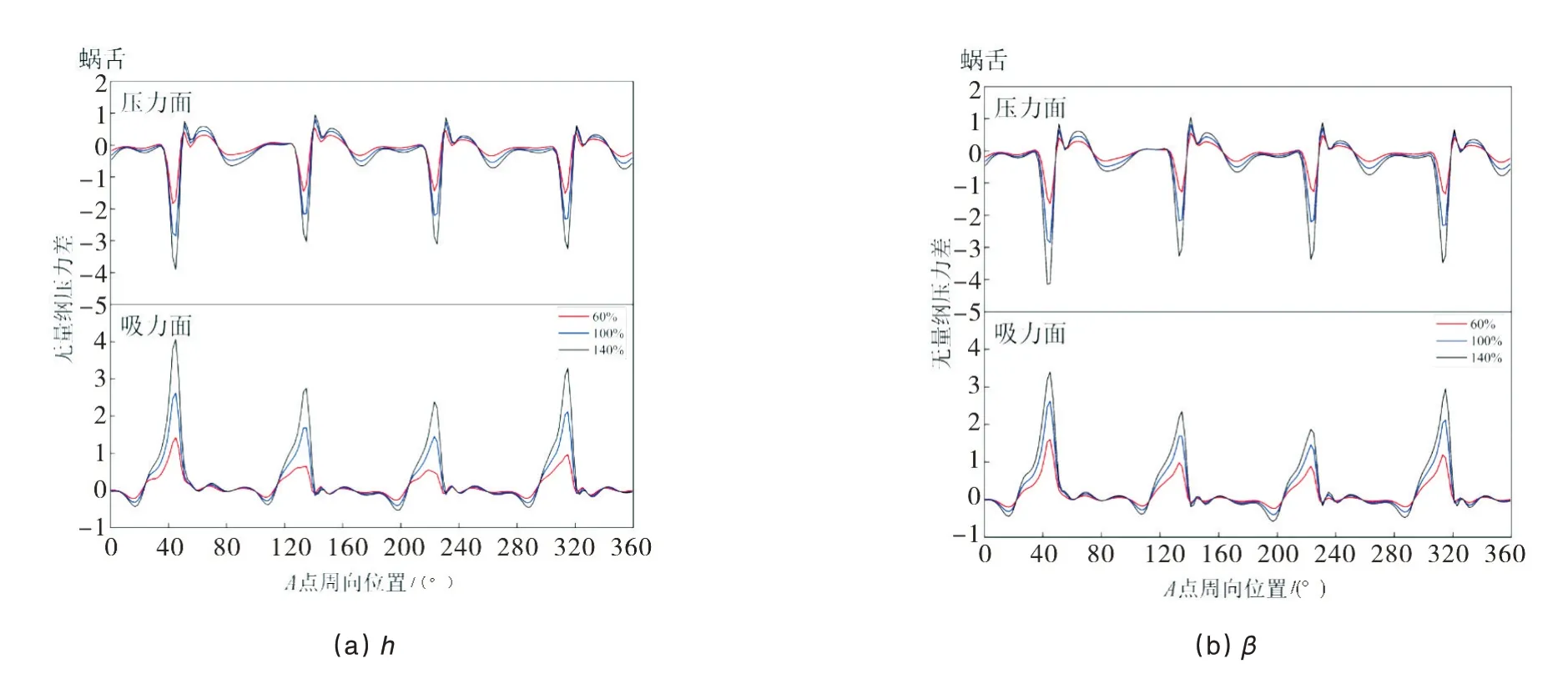
图11 关键尺寸参数对A点压力差的影响Fig.11 Influence of key parameters on pressure difference at point A
3 结论
叶片的高周疲劳是无喷嘴径流涡轮损坏的最常见原因。当前的叶片抑振方法具有周期长、通用性低、牺牲气动性能等缺陷。本文研究了基于机匣处理的无喷嘴径流涡轮叶片抑振方法。以下是主要结论:
1)采用广义力指导抑振流动控制方法的设计,提出一种基于机匣处理的新型抑振方法。在叶片出口机匣壁面设计4个沿周向均匀分布的直槽,以抵消蜗壳产生的气动激振力。
2)研究了蜗舌与直槽间的相对位置(相对角)对气动激振的影响。当相对角为45°时,振幅下降了46%。广义力和流场分析表明,蜗壳与直槽的激振效应在该角度下抵消。因此,将45°视为相对角的最优值。
3)研究了直槽尺寸参数对叶片激振的影响。结果表明,通过合理调节参数,振幅最多下降了94%。4 个尺寸参数中有三个参数(d1,h,β)对振幅有显著影响。参数d1同时影响Fcasing的长度与相位,这因为直槽与叶片方向的不一致。参数h和β只影响Fcasing的长度而不改变其相位,极大地方便了直槽的设计,因此将其视为关键参数。压力分析表明,关键参数只影响机匣处理所引起的4 阶谐波压力的幅值而不改变相位,因此,Fcasing的相位不受关键参数影响。
- 风机技术的其它文章
- Study on Loss Quantitative Analysis Methodology for Highly-loaded Transonic Fan*
- Influence of Change Law of Blade Leading-Edge Ellipse Ratio on Inception Cavitation Performance of Centrifugal Pump*
- 带诱导轮的离心式航空燃油泵空化特性分析*
- Optimization Design of Air Conditioning Outdoor Unit Top Plate Based on Orthogonal Test
- 重燃透平叶片真实内部冷却通道的传热特性研究*
- Numerical Study of Film/Shock Interaction on Suction Surface of Transonic Turbine Cascade*

