行星探测光学导航方法及误差分析
吴 鹏,穆荣军,邓雁鹏,崔乃刚
(哈尔滨工业大学 航天学院,哈尔滨 150001)
环形山具有明确、稳定、易于提取结构等优点,广泛分布于月球[1]、火星[2]、小行星[3]、卫星[4]等天体表面,环形山图像匹配被广泛应用于光学导航中。环形山检测算法(Crater Detection Algorithm,CDA)是在探测器获取的光学图像或激光高程信息基础上,提取图像中环形山的算法。环形山检测方法众多,目前已有采用形态学、明暗分析、Canny 边缘检测、卷积神经网络、深度学习、极大熵阈值三值化[5]等算法的CDA 得以提出并应用于月球及行星探测中[6-9]。CDA及因其而发展的曲线拟合、半圆拟合等方法应用广泛,相应算法在行星际航行的天文导航中也有应用[10]。
近年来,随着月球、火星等深空探测任务的实施与发展,众多研究者针对基于环形山检测的光学导航算法(CDA based Optical Navigation,CDA-OPNAV)开展研究,将其与惯导进行组合,获得了较为丰富成果。文献[11]对基于特征的可观测性进行分析,并采用Fisher 信息计算误差下界;美国火星漫游者号采用序列图像特征点提取和匹配的方式进行相对导航[12];文献[13]进一步将特征点观测扩展为特征点矢量信息与惯导系统进行组合,但仍存在难以计算地理系下绝对导航参数等问题;Cui 等研究者将曲线特征引入系统中,基于环形山边缘曲线特征实现了较高精度的光学导航[14]。在以往研究中,主要存在以下两方面问题:一是对特征信息利用不充分,未能充分挖掘探测器在空间中所处位置的分布特性;二是对特征拟合等观测误差在OPNAV 系统中的传递关系缺乏明确分析与有效处理。
本文提出一种基于探测器空间位置分布(Spatial Position Distribution)模型的光学导航方法。在实现鲁棒环形山检测后,以阿贝尔李群空间圆环面描述探测器在获取天体表面特征条件下,其所在位置的空间分布,形成Torus-OPNAV 导航方法;将其与惯导进行组合,实现行星探测器高精度导航。在此基础上,用成像余弦方差贡献函数描述了环形山拟合误差对光学导航定位、定姿的影响。
1 环形山检测及考虑误差的椭圆拟合
将月面环形山建模为椭圆,方程如式(1),X为环形山边缘灰度坐标点集,A、b为椭圆参数矩阵。

采用最小二乘法计算式(2)中的参数A和b。


因此拟合后的椭圆中心坐标Xo为:
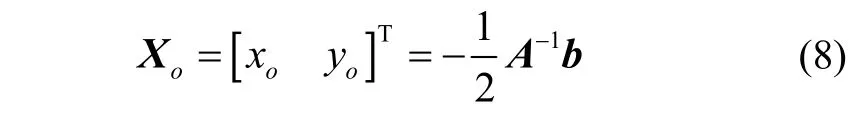
2 基于环形山检测的探测器光学导航方法
2.1 光学导航成像测量模型
构建环形山成像齐次坐标系Puv、环形山中心的月表固连地理系齐次坐标系Pf和相机系PC。

环形山j成像模型如式(12),U i、V i为环形山Xi成像等效坐标,f为焦距。

将探测器位姿信息与光学成像结果联系起来:

CDA-OPNAV 就是求式(10)(11)中12 个待解变量。
2.2 Torus-OPNAV 探测器空间定位分布模型
传统基于环形山探测信息的探测器定位方法通常需要4 座环形山。当环形山数量低于4 座时,为保障导航系统正常运行,常以观测矢量误差为观测量构建误差传递方程进行导航。部分观测条件下,探测器位置求解的解空间可能呈现扁平特征,如图1 所示,给迭代求解方法带来挑战。
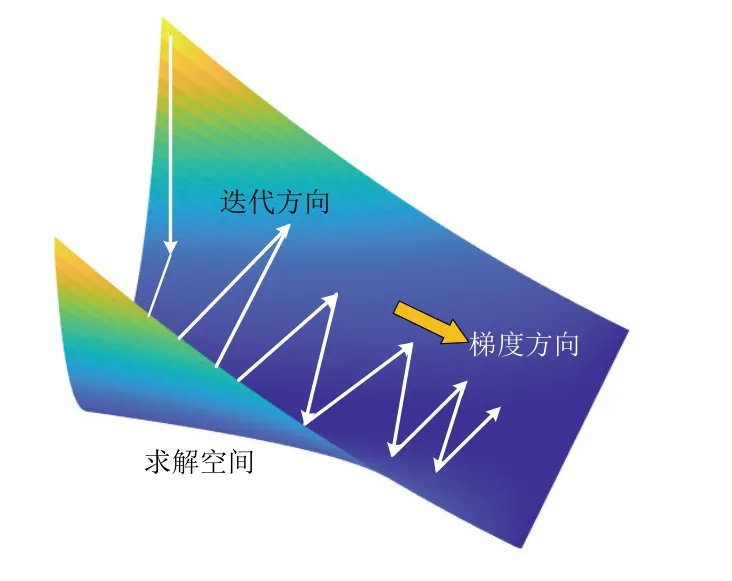
图1 光学导航求解空间及梯度方向Fig.1 Solution space and gradient direction of OPNAV
此外,当提取出的环形山等特征地形较多时,为提升算法效率,需要从所有探测环形山中选取几座进行光学导航,这使得光学导航解算结果无法达到最优。文献[11]通过计算Fisher 信息矩阵和Cramer-Pao 界,分析了n个特征地形条件下,光学导航位置估计误差下界:

式中,Fn为Fisher 信息矩阵、σu为量测噪声方差、zc为观测特征在相机坐标系下z方向投影。式(14)表明,探测器高度一定时,位置估计误差下界随探测特征增加而减小。实际过程中通常采用几何分布法、信息熵法选取若干环形山进行导航解算,误差下界难以满足导航系统设计需求,因此要充分挖掘光学探测信息,分析误差传播特性的一般形式。

考虑环形山非齐次坐标和探测器位置坐标:


图2 探测器空间位置分布示意图Fig.2 Spatial position distribution diagram of lunar probe
图2 描述的曲面是圆环面T2,定义为两个圆之积,是一个阿贝尔李群[16]。

光学导航中圆环面(Torus)可由一组参数方程得到。参数方程包含两部分:一部分为描述空间中定圆L的点集Pl∈L,另一部分为描述空间中探测器所处曲面S的点集P s∈S。
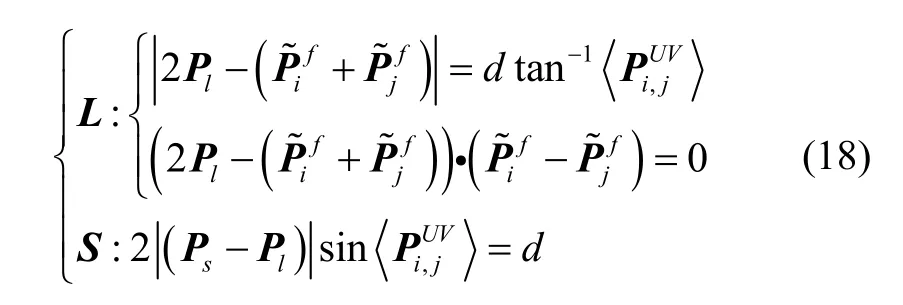
式中,d为两环形山间欧氏距离。当给定三座环形山时,可构建出三组约束{L,S}对探测器所在位置P进行精确计算。

三组约束能得出4 个符合约束的解,如图3 所示,探测器位于其中一个解所在的位置。结合高度约束h> 0及速度方向约束,可唯一确定探测器在k时刻所处位置Pk,如式(20)所示。式中,为k时刻i点位置,[Pk]z为Pk在竖直方向投影。

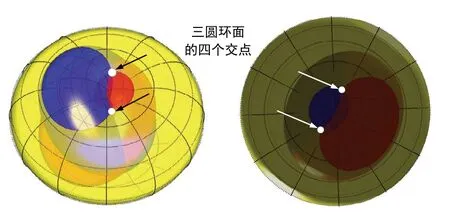
图3 三个曲面形成四个交点示意图Fig.3 Four intersections from three surfaces
根据式(13),给定探测器位置信息后,姿态信息与定位结果解耦,可直接进行计算。考虑环形山成像过程中的所有环形山地理系坐标和相机系坐标PC,它们之间有如下转换关系:

探测器姿态为:

3 拟合误差分析及其对导航系统的影响
3.1 环形山最小二乘拟合误差分析
环形山探测误差υi服从正态分布[17]。

对式(24)进行Taylor 展开,仅考虑一阶项:
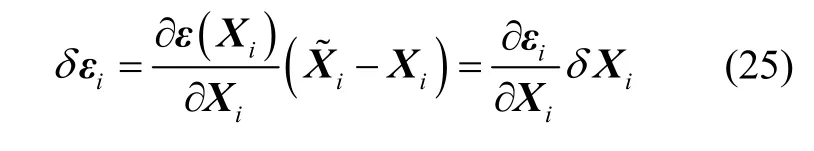
将式(2)(3)代入式(25)中,得:
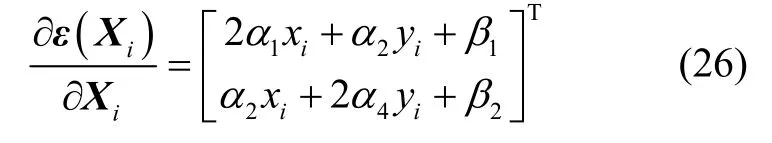
则环形山观测残差方差为:


修正后的测量环形山中心坐标为:

3.2 环形山拟合误差对光学导航定位的影响
由于拟合误差,椭圆圆心并不一定对应真实环形山圆心坐标。光学相机拍摄的环形山中心点像素坐标Puv也存在误差,如式(35)所示。


将式(42)代入式(39)中,
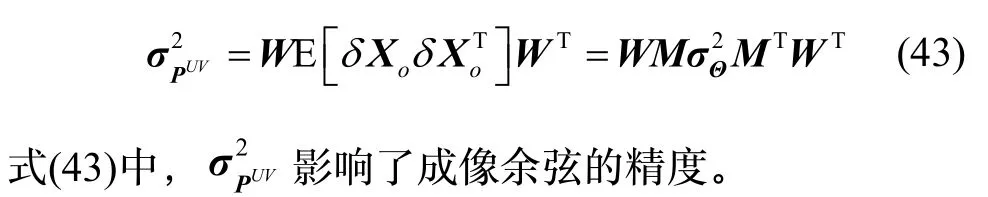
定义不含误差的中间参量ti,tj和gi,j:
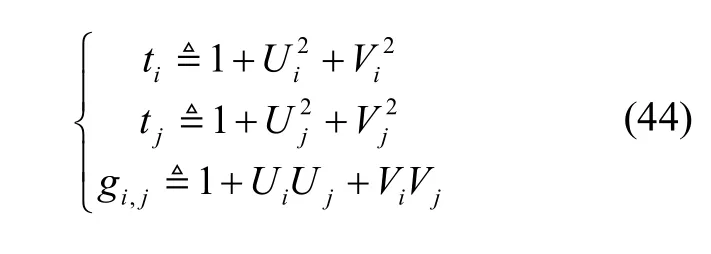
定义含有误差的参数项λi,j,γi,j和φ:

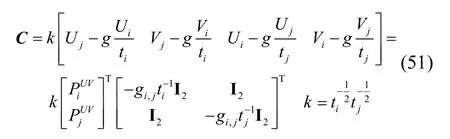
将式(50)代入式(39)中,得:

联立式(27)(33)(42)(52),得:
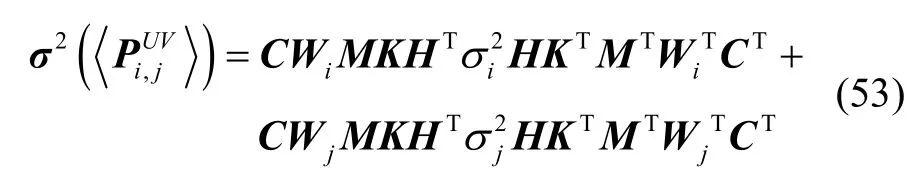
定义环形山X成像余弦方差贡献函数 Ψ(X):

用环形山成像余弦方差贡献函数 Ψ(X)表达环形山拟合误差对光学导航定位的影响为:
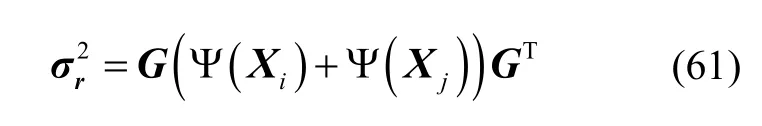
4 仿真分析
4.1 Torus-OPNAV 算法可行性验证
利用文献[5]环形山数据作为原始数据。设置仿真条件如表1 所示,进行Torus-OPNAV 仿真试验,打靶次数1000,定位和定姿结果如图4-5 所示。
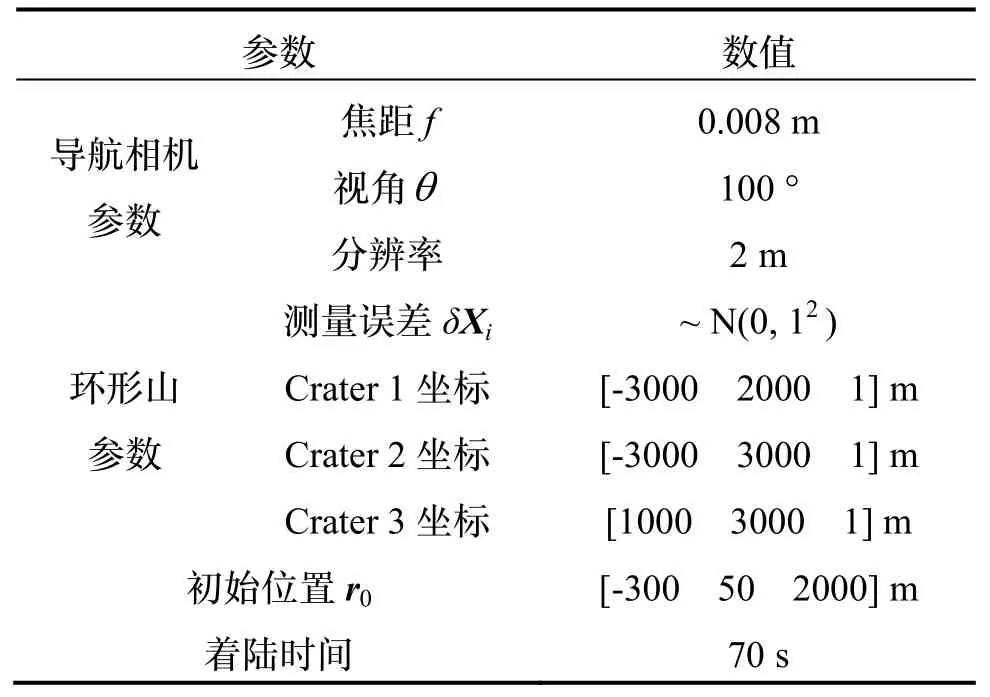
表1 仿真条件设置Tab.1 Simulation condition

图4 Torus-OPNAV 定位蒙特卡洛仿真结果Fig.4 Monte Carlo positioning results of Torus-OPNAV

图5 Torus-OPNAV 定姿蒙特卡洛仿真结果Fig.5 Monte Carlo attitude results of Torus-OPNAV
在此基础上,将本文提出方法与基于特征点匹配的导航方法(Feature points matching based navigation,FPM-NAV)进行对比,选取特征点为ORB 特征点,仿真定位结果如图6 所示。可以看出,随着导航时间增加,FPM-NAV 误差逐渐积累,而Torus-OPNAV 一直维持较好的导航定位精度。

图6 Torus-OPNAV 与FPM-NAV 定位结果Fig.6 Results of Torus-OPNAV and FPM-NAV
4.2 不同观测条件下的Torus-OPNAV 仿真
在实际月球及火星等探测任务中,由于探测器搭载的导航相机分辨率和测量误差方差不同,探测的环形山坐标有所区别。设定多种导航相机测量误差方差和环形山坐标分布情况,如表2 和图7 所示。图7 为两组环形山坐标分布构型示意图。与构型1 相比,构型2 中环形山坐标跨度更大。

图7 两组环形山分布构型Fig.7 Two crater distribution configurations

表2 Torus-OPNAV 蒙特卡洛仿真条件Tab.2 Torus-OPNAV Monte Carlo simulation condition
进行蒙特卡洛仿真实验,打靶次数1000 次,结果如表3-4 所示。得出如下结论:(1)不同环形山分布构型和测量误差方差条件下,Torus-OPNAV 算法运行时间相差不大,实时性较好,在180 ms 内即可完成定位定姿;(2)Torus-OPNAV 定姿定位精度受环形山几何构型影响。环形山坐标跨度越大,定位定姿结果越好;(3)探测器天向定位精度更高,成像余弦对探测器高度更敏感。在探测器下降着陆过程中,由于探测器姿态变化、图像畸变等误差影响,在探测图像分辨率1 m/pixel,测量误差优于N(0,22)m 的情况下,基于空间位置分布模型的Torus-OPNAV 定位精度可达到米级,定姿优于6 °(3σ)。

表3 构型1 条件下蒙特卡洛仿真结果Tab.3 Monte Carlo results under Configuration 1
4.3 Torus-OPNAV 与VAIN 方法对比分析
现有的OPNAV 方法通常不单独使用,而是与惯导系统(Inertial Navigation System,INS)进行组合,采用视线矢量作为量测信息,构建行星探测器视觉辅助惯性导航系统(Vision-aided Inertial Navigation,VAIN)。因此,将本文提出Torus-OPNAV 方法与惯导进行组合,分别在2 km 和15 km 高度对月面进行随机观测,再与VAIN 方法进行对比。导航相机参数与表1 相同,INS 参数如表5 所示。

表4 构型2 条件下蒙特卡洛仿真结果Tab.4 Monte Carlo results under Configuration 2

表5 惯导系统参数Tab.5 Parameters of INS
选取出观测图像中最大的三座环形山作为定位信息,采用收敛后的位置和姿态的均方根误差(Root Mean Square Error,RMSE)作为评价指标进行评价,仿真结果如表6 所示。可以看出,本文提出方法的导航精度要好于传统的VAIN 方法。原因是在相同高度条件下,随机选定观测区域后,本文提出的Torus-OPNAV 能根据当前环形山探测结果,计算出符合这一次随机观测的方差贡献 Ψ(X),用 Ψ(X)直接替换误差方差矩阵R,进而调整导航系统对探测信息的信任程度(滤波增益K),使导航系统具有一定自适应性;而传统VAIN 方法预先设定导航系统中的误差方差矩阵R,算法性能弱于本文提出方法。其中位置精度提升约10%。

表6 Torus-OPNAV 与VAIN 导航结果对比Tab.6 Errors of Torus-OPNAV+INS and VAIN
5 结论
理论分析及仿真试验表明,与现有OPNAV 方法相比,本文提出方法有如下优势:(1)揭示了光学成像信息与探测器所处空间位置分布之间的关系,论证该位置空间分布曲面为一圆环面,并以一组参数方程对其予以描述,降低光学导航的计算量。(2)由于测量误差存在,探测得到的环形山中心及其形状与真值难以精确匹配。本文详细推导了误差在最小二乘拟合、成像余弦计算、非线性迭代等过程中的误差传播特性;并提出成像余弦方差贡献函数,以此分析环形山观测误差对光学导航定位、定姿精度的影响。(3)成像余弦方差贡献函数 Ψ(X)可直接用于调节滤波器中误差方差矩阵R,使光学导航系统对复杂环境具有适应性、提升导航精度。(4)提出方法可直接解算探测器绝对位置信息,定位精度高、实时性好。

