基于点特征的直角坐标系空间直线度偏差评价

杜红枫，陈晓航，王治忠，张乃方

（1.西安交通大学 科学与教育发展研究院，陕西 西安 710049；2.西安航天发动机有限公司，陕西 西安 710061）

0 引言

空间直线度偏差是指实际空间直线相对于理想空间直线的偏移变动量。在机械制造与检测测量领域中，准确评价空间直线度偏差具有重要意义。在大尺寸轴、孔类零件的生产和加工过程中，受加工设备、加工方式的影响使零件产生空间直线度偏差，会直接影响产品的性能、寿命和质量。因此，建立一套符合直角坐标系下的空间直线度偏差测量与评价方法十分必要。

在前期开展的研究中［1-4］，空间直线度偏差的定义与基本数学模型已被建立，为后续研究空间直线度偏差评价方法提供了良好的基础。目前，空间直线度偏差评价方法分为几何误差建模方法和参数优化方法两类。

几何误差建模方法依靠误差模型的空间几何关系建立偏差评价模型。文献［5］提出了一种空间直线度坐标测量的不确定度计算方法，以保证空间直线度坐标测量结果的完整性和有效性；文献［6］和［7］分别基于最小二乘方法提出了改进的空间直线度偏差评价模型，进而提高测量与评价的正确性。几何误差建模方法适用于数据量不大的情况，但是由于误差模型与测量结果直接相关，精确建模难度较大。为了降低建模难度，提高计算精度，文献［8］提出了一种基于切比雪夫范数的空间直线拟合模型，以提高轴线的拟合精度；文献［9］至［11］提出了不同的基于几何关系优化的空间直线度偏差线性逼近算法，在一定程度上提高了测量精度，但是计算效率有待提升。

参数优化方法的原理是将测量结果作为最优解进行寻优，本质上属于非线性优化问题，适用于传统数学计算难以处理的求解过程。文献［12］和［13］给出了基于遗传算法的空间直线度误差评定方法，遗传算法可解决几何优化中存在的不足，但变量初始变化范围及算法参数选取会在一定程度上影响结果的稳定性。为了提高计算效率，一些学者利用智能优化算法［14-15］处理测点拟合轴线的方向向量；也有一些学者研究了其它多目标优化算法，文献［16］至［21］建立了空间直线度偏差计算模型，将非线性优化问题线性化处理。由于数据处理过程中，优化目标和核心寻优策略存在差异，导致参数优化方法在一些实际应用条件下计算效率较低。

为解决目前直角坐标系下空间直线度偏差评价方法建模难度大的问题，提出了基于点特征的直角坐标系空间直线度偏差评价方法。以直角坐标系下空间直线度测量法为研究对象，建立了空间直线度偏差评价数学模型。着重研究了空间直线度偏差测量模型、基于点特征的空间直线度偏差评价模型、基于点特征的空间直线度偏差最小区域评价方法，依托模型点特征关系，高效、准确地实现直角坐标系下的空间直线度偏差评价。最后利用三坐标测量机开展测量实验，对该方法的可行性与准确性进行验证。

1 空间直线度测量模型与数学模型

1.1 直角坐标系下空间直线度的测量模型

空间直线度偏差的测量模型由测量评价空间决定。截面测量法是圆柱体几何量偏差最有效的测量评价空间模式［22］，本文提出的空间直线度偏差测量模型建立在截面测量法的基础上。如图1所示，直角坐标系下空间直线度偏差测量模型由采样、定心、拟合、评价四个部分组成，最后通过轴线的控制位置获得空间直线度偏差测量与评价的结果。

1）采样：在测量空间中通过测量仪器获得被测圆柱体具体形貌的过程被称为采样，通过采样获得被测圆柱体位置参数，使被测圆柱体以数字形式复现。

2）定心：截面测量法可获得多个截面轮廓的坐标数据，将截面轮廓坐标数据代入数学模型，可计算得出截面中心位置。计算获得多个截面轮廓中心，从而真实客观地获取多截面的共有轴线。

3）拟合：对多个测量截面中心进行线性拟合，得到空间直线度偏差测量与评价基准—圆柱体中心轴线。中心轴线是实现坐标变换的基础，也是圆柱体位置校正的基准线。

4）评价：在确定中心基准轴线后，需要对圆柱体中心轴线空间位置进行变换与投影。利用最小二乘法和最小区域法获得包容轴线的圆柱半径以对空间直线度偏差进行评价。

1.2 直角坐标系下空间直线度的数学模型

直角坐标系下空间直线度偏差的测量数据以笛卡尔坐标数据为主，这类数据由符合笛卡尔坐标系的测量仪器（如三坐标测量机、坐标投影仪等）获得。根据直角坐标系下的空间直线度偏差测量模型，将被测圆柱体放置于直角坐标系内。在圆柱体上沿轴向方向均匀选取测量截面S1，S2，…Si（所有测量截面S均与仪器测量坐标系基准测量平面平行），测量截面数N≥ 5，i= 1，2，3，…N。每个测量截面的测量点数M≥ 5，各个测量点的坐标为Pij（xij，yij，zij），j= 1，2，3，…M。如果被测圆柱体零件轴向方向与Z轴平行，单一测量截面轮廓F（x，y）可表示为

F(x,y)=C1x2+C2y2+C3xy+x+C4y+C5（1）式中：C1，C2，C3，C4，C5为空间单一测量截面的轮廓系数。

为了降低计算误差，将式（1）中x的系数设置为1。设置对称矩阵A和B，根据单一测量截面的轮廓数据，利用最小二乘法计算截面轮廓系数。A和B的表达式为

则截面轮廓系数矩阵C为

其具体表达式为

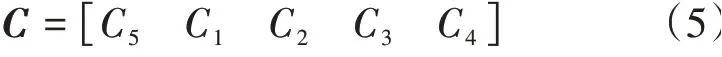
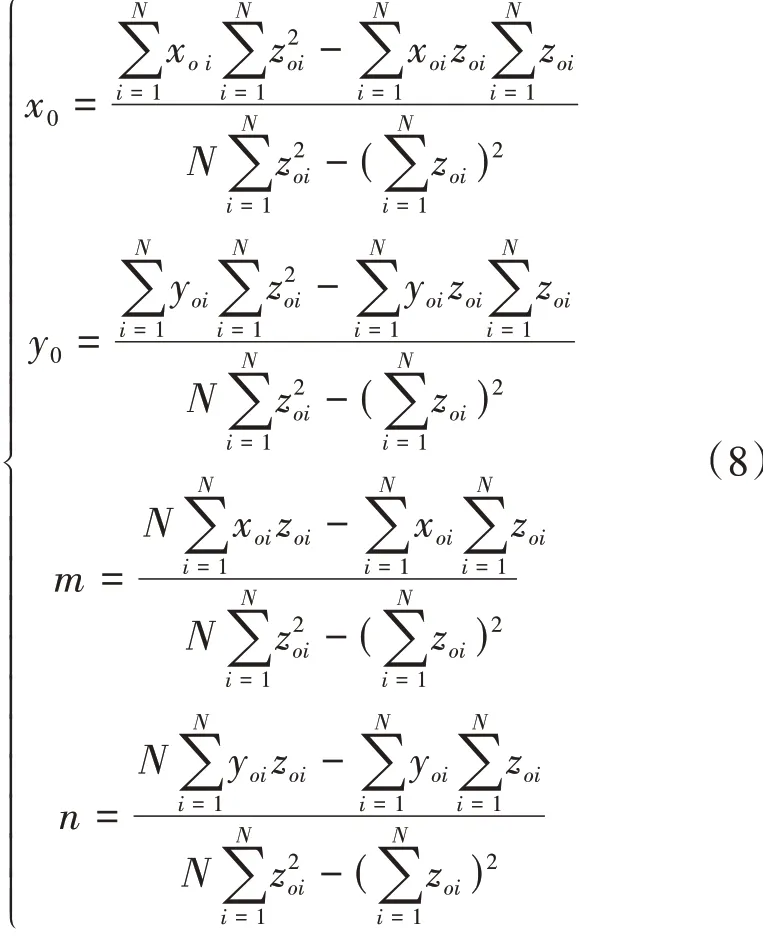
当获得第i个截面轮廓系数C1i，C2i，C3i，C4i，C5i后，可得第i个测量截面中心坐标Poi（xoi，yoi，zoi），其中

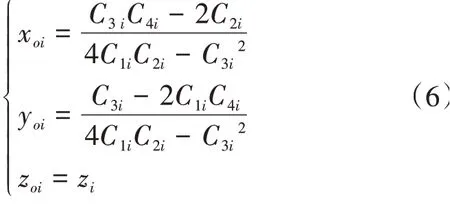
直角坐标系下空间直线度偏差评价模型的基础是确定中心轴线位置。在截面测量法中，需要对多个测量截面中心进行空间拟合处理，从而获得被测圆柱体的中心轴线。设圆柱体零件轴线的空间向量n=（m，n，1），x0和y0是空间轴线与XOY坐标平面的交点P0（x0，y0，0）的坐标，利用最小二乘法获得被测圆柱体轴线的空间表达式为

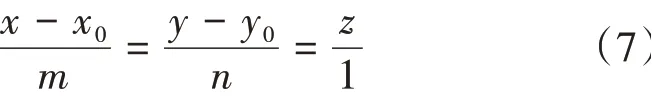
将被测圆柱体的多个测量截面中心用轴线相关联，可获得测量空间中被测圆柱体的轴线，如图2所示。

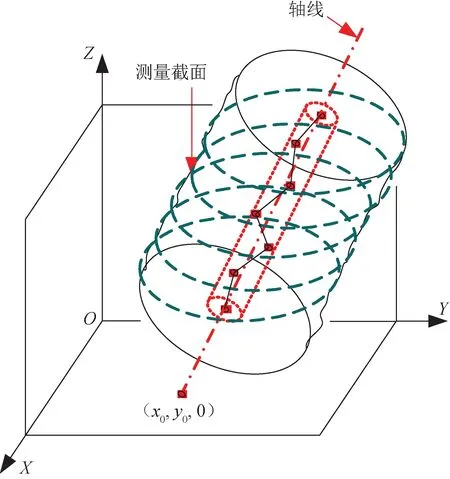
图2 圆柱体空间轴线模型Fig.2 Model of spatial axis of cylinder

通过最小二乘法对多个测量截面中心进行拟合，可获得被测圆柱体轴线表达式为

1.3 直角坐标系下测量空间中的统一

获得了被测圆柱体的空间轴线后，需要对轴线及各个测量截面中心进行坐标转化。坐标转化的实质是将测量坐标系与工件坐标系统一，从而降低计算过程中产生的误差，并提高模型计算效率。在直角坐标系下，坐标转化包括坐标的移动和转动。为了满足测量坐标转化的要求，以图2中XOY坐标平面作为基准坐标平面，由此获得的旋转与平移组合转化矩阵TXOY为

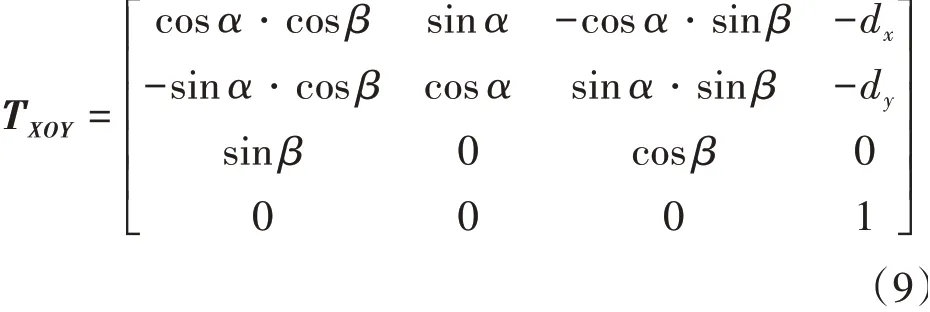
式中：α，β分别为轴线绕直角坐标系X轴，Y轴的旋转角度，分别为坐标沿X轴，Y轴的平移量。

测量坐标转换完成后，需要根据基准坐标平面对测量坐标值进行平面投影。以XOY坐标平面作为基准坐标平面，对应的投影转化矩阵为

2 空间直线度偏差评价模型

利用多个测量截面中心的空间测量坐标在基准坐标平面的投影数据对空间直线度偏差进行评价，即确定截面中心投影数据的包络区域。符合最小条件的空间直线度偏差为包络被测圆柱体测量截面中心的最小的圆柱直径，即空间包络被测圆柱体轴线的最小圆柱的直径。

2.1 空间直线度偏差最小二乘评价模型

设各个测量截面中心点到轴线的距离为Loi，则最小二乘空间直线度偏差SDLS为

最小二乘空间直线度偏差评价模型由距离轴线最远的测量截面中心确定，即“1+0”模型，该模型在投影面的结构如图3所示。

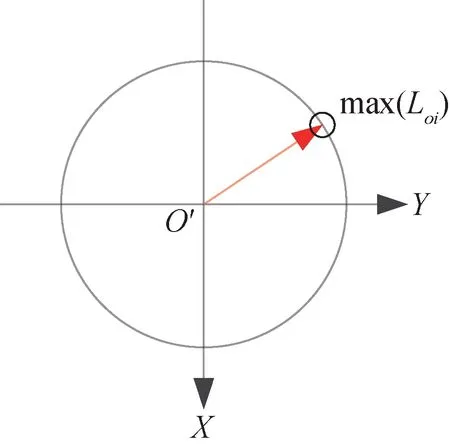
图3 最小二乘空间直线度偏差评价模型Fig.3 Model of least square evaluation for spatial straightness deviation

“1 + 0”模型是指1个特征点必须在包络所有测量截面中心的圆柱面投影轮廓上，即这个特征点距离轴线最远。另外，在具有直角坐标系的测量仪器中，空间直线度偏差的测量应尽量满足“小偏差、小误差”条件。假设测量误差足够小，且可以降低被测圆柱工件轴线的位置误差，为了降低测量误差对测量结果的影响，采样点数量应为偶数，且采样点在测量路径上应等间隔分布。

2.2 空间直线度偏差最小区域评价模型

最小区域空间直线度偏差是符合最小条件评定要求的。按照最小条件评定空间直线度偏差的本质是寻找最优的被测圆柱体空间直线位置，进而获取Loi的最优解。由于空间直线度偏差模型为单一包容轮廓模型，参考圆柱度偏差的最小区域评价模型，空间直线度偏差最小区域评价中包络被测圆柱体轴线的轮廓由2个点、3个点或者4个点构成，即“2 + 0”，“3 + 0”或者“4 + 0”模型，3种模型在投影面的结构如图4所示。

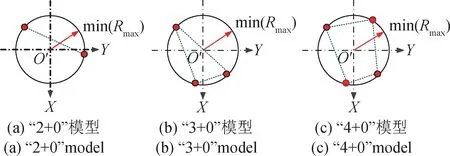
图4 最小区域空间直线度偏差评价模型Fig.4 Models of minimum zone evaluation for spatial straightness deviation

在图4中，“2 + 0”，“3 + 0”，“4 + 0”模型分别指2个、3个、4个特征点必须在包络所有测量截面中心的圆柱面投影轮廓上，且这2个点、3个点、4个点构成的投影截面轮廓圆半径R最小。三种模型均不存在内包络圆柱面，因此无内包络圆柱特征点，这与圆柱度偏差评价模型存在区别。“2 + 0”模型是“3 + 0”模型的退化形式，“4 + 0”模型是“3 + 0”模型的进化形式，三种模型中形成的包络截面轮廓的最小外接圆直径即为最小区域空间直线度偏差SDMZ，其表达式为

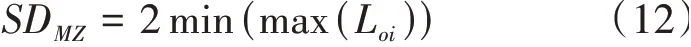
3 基于点特征的空间直线度偏差最小区域评价

基于点特征的空间直线度偏差最小区域评价建立在空间直线度偏差最小二乘评价的基础上。基于点特征的最小区域评价由最小二乘评价模型演化而来。首先将被测圆柱的空间轴线和各个测量截面中心进行空间坐标转化，之后以圆柱体轴线作为投影轴对测量截面中心进行投影，然后利用最小二乘方法获得投影测量数据的轴心位置，并完成数据的初始处理。

在测量坐标系投影面上，通过投影点获得被测圆柱体最小二乘中心轴线投影点Op后，以Op点为坐标原点对各测量点的坐标进行平移，获得各点坐标值P'oi（x'oi，y'oi），然后依据各测点坐标构建空间直线度偏差最小区域评价模型。具体步骤为：

1）在投影平面内，从P'oi中找出距离Op最远的采样点M1（xM1，yM1），以及距离M1最远的点M2（xM2，yM2）。

2）由M1，M2通过弦线截交关系中心V1（xV1，yV1）。由式（13）计算P'oi到V1（xV1，yV1）的距离，搜寻距离V1最远的点M3（xM3，yM3）。

若|V1M3| ≤ |V1M1|，则M1，M2为“2 + 0”模型的特征点，空间直线度的偏差为2|V1M1|；若|V1M3| >|V1M1|，则M1，M3继续通过虚拟中心迭代。

3）当M1，M2，M3迭 代 不 发 生 变 化 时，M1，M2，M3为“3 + 0”模型的特征点。通过3个点计算特征圆的圆心V2（xV2，yV2）的坐标为

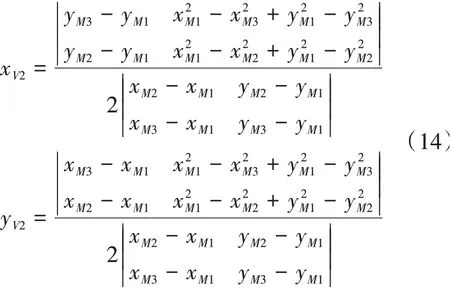
4）计算P'oi到V2的距离，搜寻距离V2最远的点M4（xM4，yM4）。若|V2M4| ≤ |V2M1|，M1，M2，M3构成“3 + 0”模型，空间直线度偏差为2|V2M1|；若|V2M4| > |V2M1|，M1，M2，M4继通过3个点计算特征圆的圆心进行迭代。

5）当M1，M2，M4迭代不发生变化时，M1，M2，M3，M4为“4 + 0”模型的特征点。通过四点计算特征圆的圆心V3，空间直线度偏差为2|V3M1|。由于空间坐标的特殊性，“4 + 0”模型实质是“3 + 0”模型的进化形式。

4 空间直线度偏差测量与评价的实验测试与验证

为了验证基于点特征的直角坐标系下空间直线度偏差评价方法的有效性，结合实际测量件对研究内容进行验证。测量对象为柴油内燃机活塞头部（缸内导引面），需根据实测数据获得活塞头部形状与轮廓误差。利用HEXAGON Global Class SR 575型三坐标测量机来测量和评价活塞活头部5 ~ 25 mm处的直线度偏差，要求空间直线度偏差控制在0.05 mm以内，测量截面采样点数为400，测量截面数量为11个。实验装置如图5所示。

图5 实验装置图Fig.5 Experimental setup

实验中，三坐标测量机的最大允许误差（MPEp）为2.3 μm，定位可重复性为0.5 μm，实验室温度条件为20 ℃。三坐标测量机测头分别对被测活塞头部圆柱面测量5次，测量结果如表1所示。由测量结果中可知：最小二乘空间直线度偏差为0.0276 mm，最小区域空间直线度偏差为0.0246 mm；被测活塞头部轴线的X，Y方向向量接近于0，说明Z轴方向向量为1，证明坐标轴之间的误差很小；最大测量相对误差为1.5 μm，并且空间直线度偏差均小于0.05 mm符合要求，证明了基于点特征的直角坐标系空间直线度偏差评价方法的有效性与准确性。

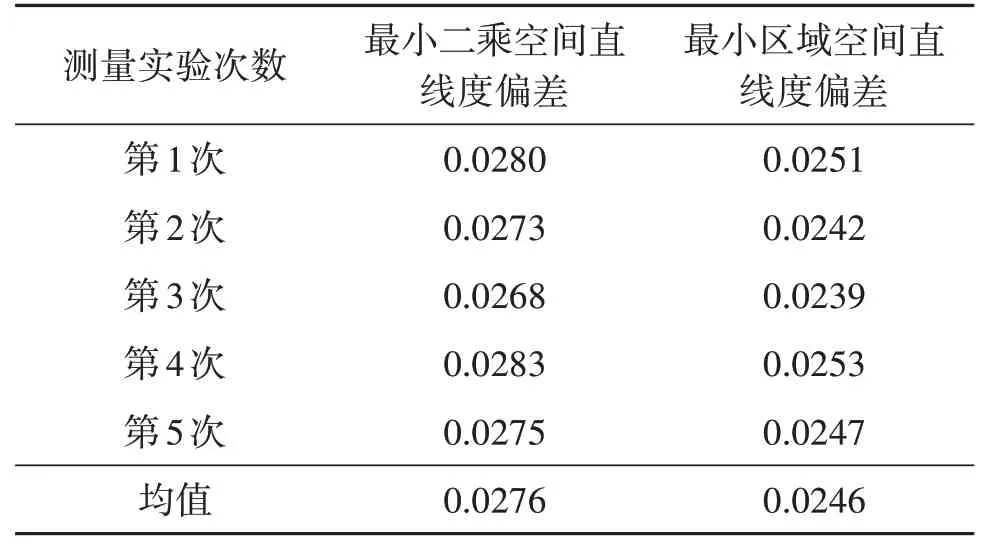
表1 活塞头部空间直线度偏差测量结果Tab.1 Measurement results of spatial straightness deviation of the piston head mm

5 结论

在分析现有空间直线度偏差评价方法特点的基础上，提出了基于点特征的直角坐标系下空间直线度偏差评价方法。根据评价模型的点特征关系，建立了直角坐标系下最小区域空间直线度偏差评价方法。重点研究了空间直线度偏差测量的数学模型，以及基于点特征的空间直线度偏差最小二乘和最小区域评价模型，有效降低了评价过程中的建模复杂度，提升了运算效率。该方法可广泛应用于直角坐标系下圆柱体类零件的空间误差测量领域，对于控制圆柱体类部件的加工质量具有重要意义。