基于流固耦合的降排截水法影响因素权重分析★
赵 谊,谭文超,杨雅铄,张 宇,卢 斌,谢兴华
(1.中国电建集团贵阳勘测设计研究院有限公司,贵州 贵阳 550081;2.河海大学水利水电学院,江苏 南京 210024; 3.南京水利科学研究院,江苏 南京 210029)
1 概述
为解决土地资源紧张,实现城市可持续发展等问题,地下空间的开发成为必然趋势[1]。地下结构相较于地上结构,会受到浮力的影响,受力情况更为复杂,对于自重不能抵抗浮力的地下结构,会出现地下结构抗浮失稳的现象。地下结构存在抗浮失稳危险时,需要采取相应的抗浮措施进行抗浮。根据抗浮措施作用机理的不同,抗浮措施可分为主动抗浮措施和被动抗浮措施[2]。被动抗浮措施主要通过提高抗浮力来满足抗浮稳定,如压重抗浮、抗浮桩、抗浮锚杆等方法。主动抗浮措施主要通过降低水浮力来满足抗浮稳定,如降排截水法。被动抗浮措施通常不够经济,而降排截水法抗浮效果较好,且经济实用,故在实际工程中具有重要意义。
降排截水法(也称泄水减压法)是通过降水、排水、截水等处理措施直接降低地下结构所受到的浮力,它的原理是通过布置系统性的降排水设施,降低地下水位,进而减少地下结构所受的浮力,以此来达到抗浮稳定[3]。但降排水时需要注意,降水过多会导致地面沉降、墙体变形等问题[4],因此在采取降水措施时,通常结合截水措施,如隔水帷幕,来减小由降水引起的沉降问题。此外,当基底附近存在弱透水层时,弱透水层可以和隔水帷幕一同将基坑与内部和外界水隔绝开来,可大大减小对坑外土体、建筑的影响,故降排截水法适用于基底附近存在弱透水层的工程。
关于降排截水法影响因素的分析已有许多学者进行研究,Zhou Nianqing等[5]发现降水引起的地面沉降、地基变形等问题,可通过设置地下连续墙有效控制,张尧[6]认为止水帷幕与泄水孔抽水量对水位降深的影响显著,Feng Shilun等[7]研究了降排截水法中基坑的空间效应,刘洋[8]对泄水减压法的主要影响因素进行了敏感性分析,Zeng Chaofeng等[9]发现时间效应和尺寸效应是影响基坑变形的两个主要因素,常西阳[10]认为地下水渗流作用对基坑变形的影响较大。目前虽对降排截水法影响因素的分析较多,但对于各个影响因素的权重分析仍然较少,本文将针对降排截水法影响因素的权重进行分析。
2 数值模拟模型
2.1 模型与材料参数
模拟基坑深5 m,占地12 m×12 m,取基坑的1/4作为对称模型计算,对称模型尺寸为31 m×31 m×25 m(长×宽×高)。初始地下水水位设置与地面齐平,采用降排截水法施工时在基坑四周设置混凝土墙作为隔水帷幕,墙深入地下10 m,厚0.5 m。土层模拟三层,即砂土层中夹杂3 m厚的黏土层,模型土层及基坑结构如图1所示。土体采用的本构模型为摩尔-库仑模型,土层特性见表1。
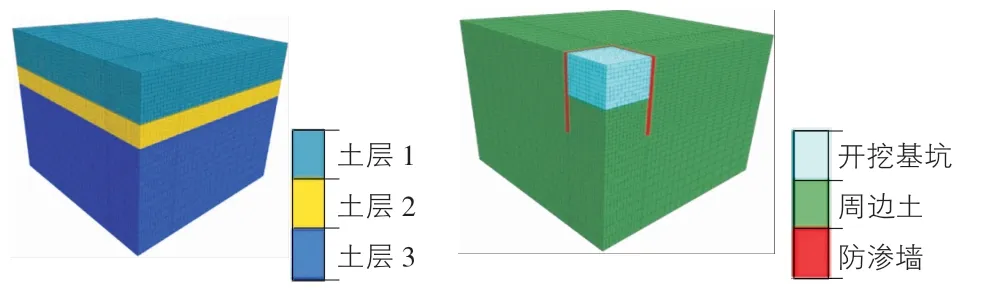
图1 模型土层及基坑结构

表1 土层力学与渗流特性表
2.2 边界条件与计算步骤
采用流固耦合分析方法进行数值模拟计算,模型的边界条件主要分为力学边界条件及流体边界条件,力学边界条件主要约束侧面及底面法向方向位移,地表位移不受约束;流体边界条件主要固定距基坑较远处的x=31 m及y=31 m边界的孔压,其余边界设为不透水边界。
模拟计算的步骤主要为:构建土体与隔水帷幕的计算模型;设置自重应力场及流体条件,计算使得模型达到初始平衡;将初始地应力平衡状态下的位移与速度归零,设置隔水帷幕,并达到应力平衡;对基坑进行开挖与降水,并在基坑底部设置泄水孔,泄水孔处孔压为0,进行流固耦合分析。初始孔压、设置隔水帷幕后的孔压云图见图2。
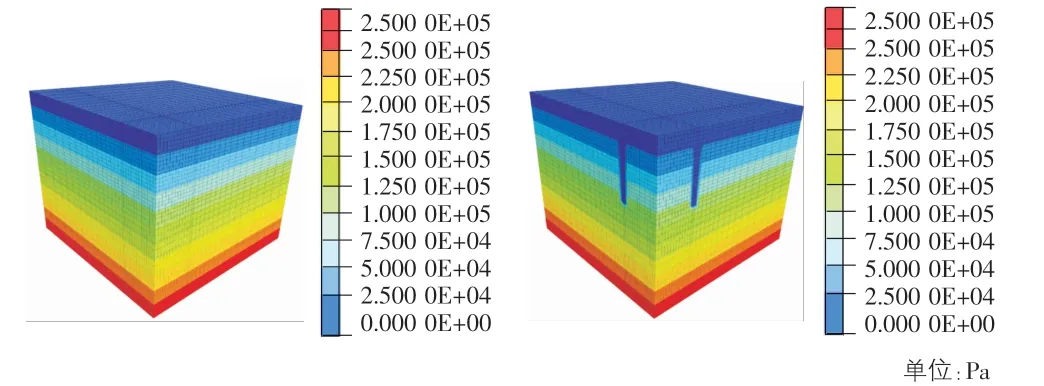
图2 初始状态与设置防渗墙后的孔隙水压力图
2.3 影响因素与工况
基于上述初始模型条件,对泄水孔数量、泄水孔间距、弱透水层厚度、弱透水层渗透系数及弱透水层相对位置5个影响因素进行分析,根据各影响因素调整各个工况采用的基础数据,共模拟15组工况,各个工况的基本参数如表2所示。
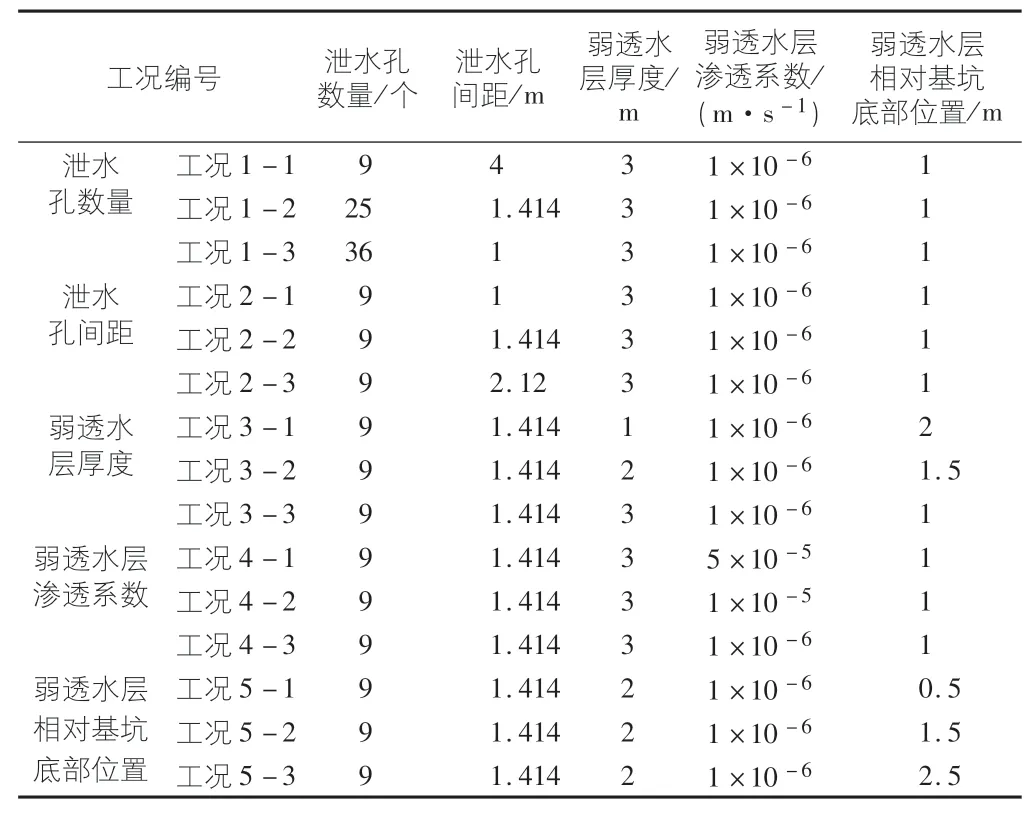
表2 数值模拟工况表
各工况下均通过设置监测点监测的沉降量来分析抗浮效果,以6 m×6 m基坑为坐标轴,监测点布置如图3所示。
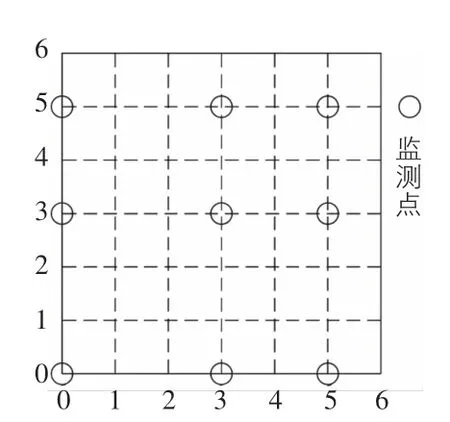
图3 沉降监测点示意图
3 模拟结果分析
以弱透水层厚度工况为例展示监测点沉降量和孔压模拟结果,由图4可见,当弱透水层越厚时,基底的孔隙水压力明显减小,各监测点处的沉降量越小。说明弱透水层起到了阻水作用,将基坑内的水与基坑外的水阻隔开来,对基坑内进行降水时,阻隔坑外水向坑内渗流。这也正是降排截水法的作用机理,通过基坑四周设置的防渗墙与基底的弱透水层组成一个隔水层,尽量减小基坑降水时对坑外地下水位的影响。
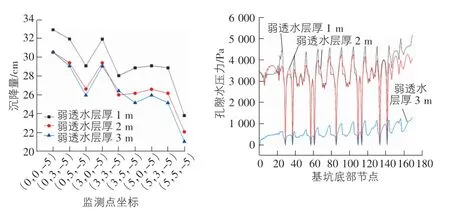
图4 弱透水层厚度工况监测点沉降及孔压结果
随着弱透水层厚度的增加,各监测点的沉降差距减小,说明弱透水层的厚度对基坑底部的影响存在极值,当超过了这个极值之后,弱透水层的厚度对基坑底部的影响变化不大。对于一个工程,主要起到隔水作用的弱透水层厚度应该是一定的,当达到这个最佳厚度时则有较好的防渗效果,对于基底弱透水层厚度与最佳厚度相差较小时,可以考虑对基底土体进行处理来优化抗浮效果。
各工况基坑底部沉降量见图5,其中工况5-1沉降量最大,为34.07 cm,工况1-3沉降量最小,为28.69 cm。为了对比各影响因素权重,采取基坑底部的平均沉降作为标准值进行分析。
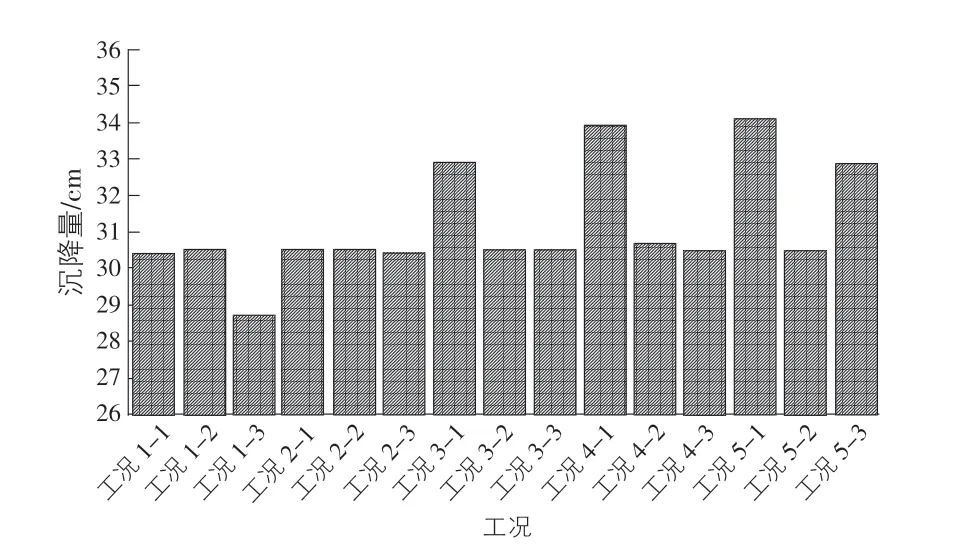
图5 各工况基坑沉降量对比
4 影响因素权重分析
4.1 层次分析法计算
采用层次分析法,对泄水孔数量、间距、弱透水层厚度、渗透系数以及相对位置这5个影响因素进行权重分析。采用层次分析法来计算影响权重时,首先需要构建层次分析模型,层次结构模型有3层,分别为目标层、准则层以及对象层[11]。决策的目标即影响因素的权重,准则选为基坑的沉降量,对象即这5种影响因素。
通过回归分析法,对5种影响因素和沉降量进行回归分析,计算得出标准回归系数见表3。
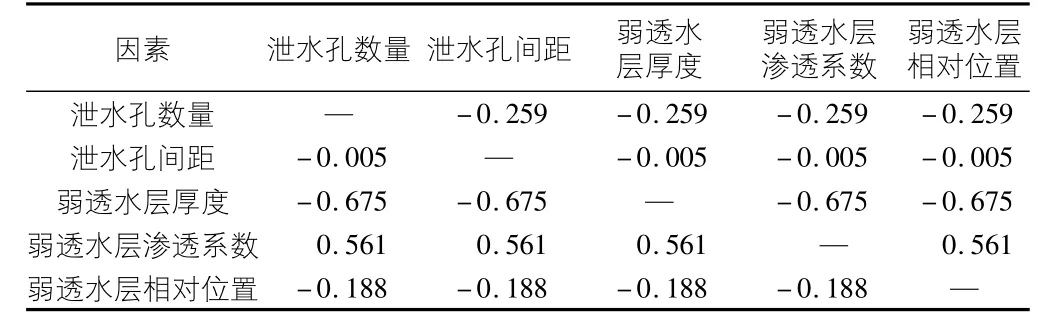
表3 标准回归系数
根据标准回归系数可计算得出每两种影响因素的相对重要性比值,即两种影响因素标准回归系数比值的绝对值,通过任意两种影响因素的相对重要性比值可构建层次分析法的判断矩阵A[12]。
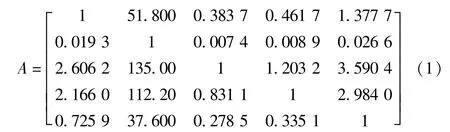
经计算得到判断矩阵A的最大特征值为5,其对应的特征向量进行归一化后为ω=(0.154,0.003,0.400,0.332,0.111)T。ω中的各元素即为各影响因素的权重值。
4.2 一致性检验
由于在计算分析模型的过程中,不可避免地会存在误差,因此需要进行一致性检验。验证判断矩阵A的一致性时则需要计算检验系数CR,当CR<0.1时,认为判断矩阵A具有满意的一致性,否则就需要对判断矩阵进行适当修正并重新进行一致性检验。计算检验系数CR时引入了一致性指标CI这一概念:

其中,λmax为判断矩阵A的最大特征值;n为判断矩阵A的阶数。当CI=0时,判断矩阵具有完全的一致性;CI接近于0时,判断矩阵有较满意的一致性,CI越大,不一致越严重。为了衡量CI的大小,又引入了随机一致性指标RI这一概念,随机一致性指标RI与判断矩阵A的阶数有关,RI的取值见表4。

表4 随机一致性指标
检验系数CR即为一致性指标CI与随机一致性指标RI的比值,即:

通过计算得出判断矩阵A的最大特征值为5,而其阶数也是5,因此计算得出一致性指标CI=0,判断矩阵A具有完全的一致性。
4.3 影响因素权重分析
泄水孔数量、泄水孔间距以及弱透水层厚度、渗透系数以及其相对位置的影响因素权重分别为0.154,0.003,0.400,0.332,0.111。其中弱透水层的厚度影响权重最大,弱透水层的渗透系数次之,泄水孔的间距影响权重最小。且弱透水层的厚度、渗透系数、相对位置三个影响因素的权重之和为0.843,故而可以认为弱透水层是影响降排截水法的最重要影响因素,其中尤以弱透水层的厚度与渗透系数为甚。
5 结论
1)降排截水法的隔水帷幕与基底附近的弱透水层形成隔水区,通过降低基坑内地下水来降低地下结构所受浮力,对基坑周围建筑影响较小,且其具有良好的经济性,因此在实际工程中具有重要意义。2)降排截水法中,弱透水层的厚度影响因素权重最大,为0.400;弱透水层渗透系数的影响因素权重次之,为0.332;泄水孔数量、泄水孔间距以及弱透水层相对位置的影响因素权重分别为0.154,0.003,0.111。3)弱透水层相关的影响因素,即弱透水层的厚度、渗透系数、相对位置3个影响因素,其权重之和为0.843,权重占比较大。故而可认为弱透水层是影响降排截水法的最重要影响因素,其中尤以弱透水层的厚度与渗透系数为甚。4)降排截水法通常用于基底附近存在弱透水层的工程,在实际工程中,可通过一些地基处理措施改善基底的透水性能,优化降排截水法的抗浮效果。

